Day 19 카메라 - 1인칭 카메라, 팔로우 카메라, 궤도 카메라, 스플라인 카메라
1인칭 카메라
1인칭 카메라(first-person camera)는 게임 세계상에서 움직이는 캐릭터의 시점에서 게임 세계를 보여준다. 이런 타임의 카메라는 FPS 게임이나 일부 RPG, 그리고 스토리텔링 기반의 게임에서도 볼 수 있다. 카메라는 플레이어 캐릭터가 게임 세계를 어떻게 움직여야 할지를 플레이어에게 알려준다. 즉 카메라와 이동 시스템의 구현은 서로 의존적이다. PC에서 1인칭 슈터 게임의 일반적인 컨트롤은 키보드와 마우스를 사용한다. W/S 키는 앞귀로 이동하고 A/D키는 캐릭터를 좌우로 이동시킨다. 마우스를 위쪽이나 오른쪽으로 움직이면 상향축을 기준으로 캐릭터를 회전시킨다. 그리고 마우스를 위아래로 움직이면 캐릭터는 가만히 두고 오직 시점만을 조정한다.
기본 1인칭 이동
시점을 구현하는 것보다 이동을 구현하는 것이 더 쉬우므로 우선 이동 구현을 먼저 한다. 1인칭 이동을 구현하는 FPSActor라는 새 액터를 만든다. 현재 MoveComponent의 앞/뒤 이동은 3D 세계에서도 잘 동작한다. 좌우 이동 구현은 몇 가지만 갱신하면 된다. 먼저 Actor에 GetForward와 같은 GetRight 함수를 만든다.
Vector Actor::GetRight() const {
// 쿼터니언 회전을 사용해서 단위 오른 축을 회전시킨다
return Vector3::Transform(Vector3::UnitY, mRotation);
}다음으로 캐릭터가 좌우로 이동하는 속도에 영향을 주는 mStrafeSpeed란 새 변수를 MoveComponent에 추가한다. Update 함수에서는 좌우로 이동하는 속도값으로 위치를 조정하도록 액터의 오른 축을 조정한다.
if (!Math::NearZero(mForwardSpeed) || !Math::NearZero(mStrafeSpeed)) {
Vector3 pos = mOwner->GetPosition();
pos += mOwner->GetForward() * mForwardSpeed * deltaTime;
// 좌우 이동을 토대로 위치 갱신
pos += mOwner->GetRight() * mStrafeSpeed * deltaTime;
mOwner->SetPosition(pos);
}FPSActor::ActorInput에서는 A/D 키를 감지할 수 있으며, 좌우 이동 속도 조절이 가능하다. 이제 캐릭터는 표준 1인칭 WASD 컨트롤로 이동한다. 왼쪽/오른쪽 회전 또한 MoveComponent가 각속도를 사용해서 처리한다. 그래서 다음으로 할 작업은 마우스 왼쪽.오른쪽 움직임을 각속도로 변환하는 것이다. 먼저 게임은 SDL_RelativeMouseMode를 사용해서 상대 마우스 모드를 활성화하는 것이 필요하다. 상대 마우스 모드는 현재 마우스 좌표가 아니라 프레임간 (x, y)값의 변화를 알려준다.
int x, y;
SDL_GetRelativeMouseState(&x, &y);
// 마우스 이동은 -500에서 500 사이의 값이라고 가정
const int maxMouseSpeed = 500;
// 초당 회전의 최대 속도
const float maxAngularSpeed = Math::Pi * 8;
float angularSpeed = 0.0f;
if (x != 0) {
// [-1.0, 1.0] 범위로 변환
angularSpeed = static_cast<float>(x) / maxMouseSpeed;
// 초당 회전을 곱한다
angularSpeed *= maxAngularSpeed;
}
mMoveComp->SetAngularSpeed(angularSpeed);위 코드를 보면 상대적인 x 이동을 각속도로 변환하기 위한 계산 순서를 볼 수 있다. 먼저 SDL_GetRelativeMouseState는 (x, y) 이동을 다룬다. maxMouseSpeed 상수는 프레임당 가능한 상대적인 이동의 최댓값이다. 비슷하게 maxAngularSpeed는 초당 회전의 최대값이다. x 값을 구한 뒤 maxMouseSpeed로 나누고 maxAngularSpeed를 곱한다. 이 계산 결과는 MoveComponent로 보내는 각속도를 산출한다.
피치 없는 카메라
카메라를 구현하는 첫 번째 단계는 CameraComponent라는 Component의 서브 클래스를 만드는 것이다. 다양한 타입의 카메라는 CameraComponent에서 파생된다. 그래서 일반적인 카메라 기능은 이 새로운 컴포넌트에 구현하면 된다. CameraComponent의 선언은 다른 컴포넌트 서브클래스의 선언과 같아. 새로운 함수로는 단순히 뷰 행렬을 렌더러와 오디오 시스템으로 전달하는 SetViewMatrix라는 함수가 있다. 이 함수는 protected로 선언한다.
void CameraComponent::SetViewMatrix(const Matrix4& view) {
// 뷰 행렬을 렌더러와 오디오 시스템에 전달한다
Game* game = mOwner->GetGame();
game->GetRenderer()->SetViewMatrix(view);
game->GetAudioSystem()->SetListener(view);
}FPS 카메라의 경우에는 CameraComponent의 서브클래스인 FPSCamera에다 Update 함수를 재정의한다.
void FPSCamera::Update(float deltaTime
// 카메라의 위치는 소유자의 위치
Vector3 viewForward = Vector3::Transform(
mOwner->GetForward(), q);
// 타겟의 위치는 100단위 앞에 있다
Vector3 target = cameraPos + viewForward * 100.0f;
// 상향 축은 z 단위 벡터
Vector3 up = Vector3::Transform(Vector3::UnitZ, q);
// look at 행렬을 생성한 뒤 뷰 행렬로 설정
Matrix4 view = Matrix4::CreateLookAt(cameraPos, target, up);
SetViewMatrix(view);피치 추가(높낮이)
회전에는 요, 피치, 롤 세 가지 종류가 있다. 요는 상향축을 중심으로 회전하고 피치는 측면축을 중심으로, 롤은 전방축을 중심으로 회전한다. FPS 카메라에 피치를 통합하려면 몇 가지 수정이 필요하다. 카메라는 여전히 소유자의 전방 벡터로부터 시작하지만 피치를 추가하기 위해 초가 회전을 적용해야한다. 추가 회전이 적용되면 새로운 뷰로 앞을 바라보게 된다. 이를 구현하기 위해 FPSCamera 3개의 새로운 멤버 변수를 추가한다.
// 피치의 초당 회전 속도
float mPitchSpeed;
// 소유자의 전방 벡터에서 멀어질 수 있는 최대 피치 값
float mMaxPitch;
// 현재 피치 값
float mPitch;mPitch 변수는 카메라의 현재(절대) 피치를 나타내며 mPitchSpeed는 현재 피치 방향으로 초당 회전값이다. 마지막으로 mMaxPitch 변수는 피치가 전방 벡터로부터 멀어질 수 있는 최댓값이다. 대부분의 1인칭 게임은 플레이어가 위 아래로 볼 수 있는 피치 값을 제한한다. 이런 제한을 두는 이유는 플레이어가 위를 똑바로 쳐다볼 경우 제어가 이상해질 수 있기 때문이다. 이런 경우를 막기 위해 기본 최대 피치 값으로 보통 60도(라디안으로 변환되어야 함)를 사용한다. 다음으로 피치를 계산에 넣도록 FPSCamera::Update를 수정한다.
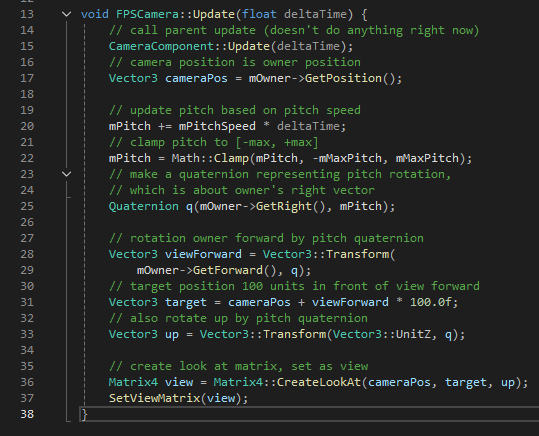
먼저 피치 속도와 델타 시간을 토대로 현재 피치 값을 갱신한다. 그리고 피치가 +/-최대 피치를 초과하지 않도록 값의 제한을 둔다. 쿼터니언은 임의의 축에 대한 회전을 나타내는 것이다. 그러므로 이 피치는 쿼터니언으로 표현 가능하다. 이 회전은 소유자의 오른 축을 중심으로 한 회전이다(피치축은 소유자의 요에 의존하기 때문에 단순히 y축은 아니다). 전방 시점은 피치 쿼터니언으로 변환된 소유자의 전방 벡터이다. 이 전방 시점은 카메라 앞에 있는 타겟의 위치를 결정하는 데 사용할 수 있다. 또한 피치 쿼터니언으로 상향 벡터를 회전한다. 그런 다음 이 벡터들로부터 look-at 행렬을 만든다. 카메라 위치는 여전히 소유자의 위치다. 마지막으로 FPSActor는 마우스의 상대적인 y 이동을 기반으로 피치 속도를 갱신한다. 피치 속도의 갱신을 위해서는 아래 코드와 같이 마우스의 x 움직임을 토대로 각속도를 계산했던 방법과 동일한 ProcessInput 코드가 필요하다.
const float maxPitchSpeed = Math::Pi * 8;
float pitchSpeed = 0.0f;
if (y != 0) {
pitchSpeed = static_cast<float>(y) / maxMouseSpeed;
pitchSpeed *= maxPitchSpeed;
}
mCameraComp->SetPitchSpeed(pitchSpeed);1인칭 모델
1인칭 모델(first-person model)은 카메라의 일부는 아니지만, 대부분의 1인칭 게임에서는 1인칭 모델을 포함한다. 이 모델에는 팔이나 발 등과 같은 애니메이션되는 캐릭터의 일부가 있다. 플레이어가 무기를 가지고 다닌다면 플레이어가 피치를 올릴 때 무기 또한 위쪽을 겨냥해야한다. 플레이어 캐릭터가 바닥에 붙어 있다 하더라도 무기 모델의 피치는 올릴 수 있어야한다. 이러한 구현은 1인칭 모델을을 위한 별도의 액터를 사용하면 가능해진다. 또한, FPSActor는 프레임마다 1인칭 모델의 위치와 회전을 갱신해야한다. 1이친 모델의 위치는 FPSActor의 위치에 오프셋을 더한 값이다. 이 오프셋은 1인칭 모델을 액터의 오른쪽에 배치시킨다. 모델의 회전은 FPSActor의 회전으로 시작한다. 그리고 추가 회전을 통해 뷰 피치를 갱신한다.
// 액터 위치에 대한 FPS 모델의 상대적인 위치 갱신
const Vector3 modelOffset(Vector3(10.0f, 10.0f, -10.0f));
Vector3 modelPos = GetPosition();
modelPos += GetForward() * modelOffset.x;
modelPos += GetRight() * modelOffset.y;
modelPos.z += modelOffset.z;
mFPSModel->SetPosition(modelPos);
// 액터의 회전값으로 회전값을 초기화
Quaternion q = GetRotation();
// 카메라의 피치 값으로 회전
q = Quaternion::Concatenate(q, Quaternion(GetRight(), mCameraComp->GetPitch()));
mFPSModel->SetRotation(q);위 코드는 위에서 설명했던 것을 코드로 보여준다. 여기서 mFPSModel은 FPSActor에서 선언한 1인칭 모델을 위한 새로운 액터이다.

팔로우 카메라
팔로우 카메라(follow camera)는 타겟 오브젝트 뒤를 따라가는 카메라이다. 이런 유형의 카메라는 카메라가 차 뒤를 따라가는 레이싱 게임과 3인칭 액션/어드벤처 게임을 포함한 수많은 게임에서 널리 사용된다. 팔로우 카메라는 여러 다양한 유형의 게임에서 사용되므로 팔로우 카메라의 실제 구현도 다양하며 변형이 많다. 1인칭 캐릭터의 예와 마찬가지로 게임이 팔로우 카메라를 사용할 때 다양한 스타일의 움직임에 대응하도록 FollowActor라는 새 액터를 작성한다. 이동 컨트롤은 W/S로 차를 전진키고 A/D키로 차를 왼쪽/오른쪽으로 회전시킨다. MoveComponent는 두 타입의 이동을 이미 지원하므로 수정이 필요없다.
기본 팔로우 카메라
기본 팔로우 카메라에서는 카메라는 항상 소유자 액터의 뒤쪽과 앞쪼긍로 설정된 거리에서 소유자 액터를 따라간다.

위 그림은 기본 팔로우 카메라의 측면 시점을 보여준다. 카메라는 차 뒤로 HDist 수평 거리만큼, 차 위로 수직 거리 VDist만큼 떨어진 거리에 배치된다. 카메라의 타겟지점은 차 그 자체는 아니고, 차 앞에있는 점 TargetPos이다. 따라서 카메라는 차 그 자체를 직접 보는 것이 아니라 차량 앞의 지점을 보게 된다. 카메라 위치를 계산하기 위해 벡터 더하기 및 스칼라 곱을 사용한다. 카메라 위치는 소유자 뒤로 HDist 단위이며, 소유자 위로 VDist 단위다. 방정식은 다음과 같다.
이 방정식에서 OwnerForward와 OwnerUp은 소유자의 전방 및 상향 벡터다. 비슷하게 TargetPos는 소유자의 앞으로 TargetDist 단위만큼 떨어져있는 지점이다.
코드에서 FollowCamera라는 CameraComponent의 새로운 서브클래스를 선언한다. FollowCamera는 수평거리(mHorzDist)와 수직거리(mVertDist), 대상 지점까지의 거리(mTargetDist)에 대한 멤버 변수를 가진다. 먼저 앞의 방정식을 사용해서 카메라 위치를 계산하는 함수를 만든다.

그리고 FollowCamera::Update 함수에서는 계산된 목표 지점과 카메라 위치를 사용해서 뷰 행렬을 생성한다.
void FollowCamera::Update(float deltaTime) {
CameraComponent::Update(deltaTime);
// 타켓은 소유자 앞에 있는 지점이다
Vector3 target = mOwner->GetPosition() + mOwner->GetForward() * mTargetDist;
// 카메라가 뒤집혀지는 경우는 없기에 위쪽 방향은 UnitZ이다
Matrix4 view = Matrix4::CreateLookAt(mActualPos, target, Vector3::UnitZ);
SetViewMatrix(view);
}이 기본 카메라는 게임 세계를 돌아다닐 때 차량을 성공적으로 추적하지만 매우 경직된 느낌이 든다. 왜냐하면 카메라는 항상 대상으로부터 고정된 거리에 있으므로 속도감을 얻기 어렵기 때문이다. 또한 차가 방향을 바꿀때 차가 방향을 바꾸는 것이 아니고 세계가 방향을 바꾸는 것처럼 봉인다. 그래서 기본 팔로우 카메라가 좋은 시작점이긴 하지만 더 좋은 방법이다. 속도감을 향상시키는 한 가지 간단한 변화는 카매ㅔ라와 소유자 사이의 수평거리를 소유자의 속도 함수로 만드는 것이다. 정지 상태에서 수평 거리(HDist)는 350 단위지만 최대 속도로 이동할때는 카메라가 따라가는 수평 거리를 500으로 증가시킨다. 이렇게 하면 차의 속도감을 느끼기 쉬워진다. 하지만 카메라는 차가 방향을 바꿀 때는 여전히 경직된 것처럼 보인다. 기본 팔로우 카메라의 경직성을 해결하기 위해 카메라에 탄력성을 추가한다.
스프링 추가
카메라 위치는 방정식에서 구한 위치를 즉각 반영하지 않고 여러 프레임에 걸쳐 목표 위치로 도달하는 형태로 구현하는 것이 가능하다. 이를 위해 카메라 위치를 '이상적인' 카메라 위치와 '실제' 카메라 위치로 분리한다. 이상적인 카메라 위치는 기본 팔로우 카메라 방정식으로부터 얻은 위치인 반면 실제 카메라 위치는 뷰 행렬이 사용하는 위치이다. 이상적인 카메라와 실제 카메라를 연결한 스프링이 있다고 하면 두 카메라는 초기에 같은 위치에 있지만 이상적인 카메라가 움직이면 스프링은 늘어나고 실제 카메라 또한 움직이기 시작하지만 느린 비율로 움직인다. 최종적으로는 스프링이 완전히 늘어나게 되고, 실제 카메라는 이상적인 카메라만큼 빠르게 움직인다. 그리고 이상적인 카메라가 멈추면 스프링은 정상 상태로 되돌아간다. 이 시점에서 이상적인 카메라와 실제 카메라는 다시 같은 위치에 있게 된다.

스프링을 구현하려면 FollowCamera에 몇 가지 멤버 변수가 필요하다. 스프링 상수(mSpringConstant)는 스프링 탄성을 나타내며 값이 클수록 탄성이 크다. 그리고 카메라의 실제 위치(mActualPos)와 속도(mVelocity)를 기록해야하므로 2개의 벡터 멤버를 추가한다.

위 코드는 FollowCamera::Update에서 스프링 처리에 대한 코드를 보여준다. 먼저 스프링 상수를 토대로 스프링 댐핑(dempaning)을 계산한다. 이상적인 카메라 위치는 이전에 구현한 ComputeCameraPos 함수의 위치 값이다. 그리고 실제 위치와 이상적인 위치의 차를 계산하고, 이 거리의 차와 이전 속도의 감쇄값을 토대로 카메라의 가속도를 계산한다. 그 다음 가속도를 이용해서 오일러 적분을 이용해 카메라의 속도와 위치를 계산한다. 마지막으로 타겟의 위치는 동일하게 유지되며 CreateLookAt 함수는 이상적인 위치가 아니라 실제 위치를 사용해서 뷰 행렬을 생성한다. 스프링 카메라를 사용하면 얻을 수 있는 큰 이점은 소유자 오브젝트가 회전하면 카메라는 그 회전을 시간을 두고 따라잡는데 있다. 이는 소유자 오브젝트가 회전할때 소유자 오브젝트의 측면이 보인다는 것을 의미하며 이 효과로 인해 세계가 회전하는 것이 아닌 오브젝트가 회전하고 있다는 느낌을 명확히 전달받는다.

마지막으로 게임시작시 카메라가 올바르게 시작하도록 FollowActor가 최초 초기화 될때 호출하는 SnapToIdeal 함수를 만든다.

궤도 카메라
궤도 카메라(orbit camera)는 대상 물체에 초점을 맞추고 그 물체 주위를 회전한다. 이런 유형의 카메라는 빌더 게임에서 사용한다. 궤도 카메라는 플레이어가 물체 주변 지역을 쉽게 볼 수 있게 해준다. 궤도 카메라의 가장 간단한 구현은 절대 세계 공간 위치보다는 대상과의 오프셋으로서 카메라의 위치를 저장하는 것이다. 이렇게 하면 카메라의 회전은 항상 원점을 중심으로 회전한다는 이점을 취할 수 있다. 그래서 카메라 위치가 대상 오브젝트로부터의 오프셋이라면 대상 오브젝트에 대한 회전을 효율적으로 구현하는 것이 좋다. 그래서 이전에 카메라와 액터의 구현과 마찬가지로 OrbitCamera와 OrbitActor를 작성할 것이다. 일반적으로 컨트롤러는 물체의 요와 피치를 적용하기 위해 마우스를 사용한다. 상대적인 마우스 이동을 회전 값으로 변경하는 입력 코드는 1인칭 카메라에서 작성한 코드와 같다. 그러나 플레이어가 오른쪽 마우스 버튼을 누를 때만 카메라가 회전하도록 제한을 추가한다. SDL_GetRelativeMouseState 함수가 버튼의 상태를 반환한다. 다음 조건은 플레이어가 마우스 버튼을 누르고 있는지 여부를 테스트한다.
if (buttons & SDL_BUTTON(SDL_BUTTON_RIGHT))OrbitCamera 클래스에는 다음과 같은 멤버 변수가 필요하다.
// 대상과의 오프셋
Vector3 mOffset;
// 카메라 상향 벡터
Vector3 mUp;
// 피치의 초당 회전 속도
float mPitchSpeed;
// 요의 초당 회전 속도
float mYawSpeed;피치 속도와 요 속도는 각 유형의 회전에 대한 카메라의 초당 현재 회전수를 기록한다. 소유자 액터는 마우스 이동을 토대로 이러한 속도를 갱신할 수 있다. 또한 OrbitCamera는 카메라의 상향 벡터뿐만 아니라 카메라의 오프셋이 필요하다. 상향 벡터는 궤도 카메라가 요와 피치 모두에서 완전한 360도 회전을 허용하므로 필요하다. 즉 카메라는 거꾸로 뒤집을수 있으므로 (0, 0, 1)과 같은 보편적인 상향 벡터를 사용할 수 없으며, 카메라가 회전함에 따라 상향 벡터를 갱신해야한다. OrbitCamera의 생성자에서 mPitchSpeed와 mYawSpeed는 둘 다 0으로 초기화한다. mOffset은 아무 값으로 초기화할 수 있지만 여기서는 물체 뒤 400단위에 있는 (-400, 0, 0) 좌표로 초기화한다. mUp 벡터는 게임 세계의 상향 벡터값 (0, 0, 1)로 초기화한다.

위 코드는 OrbitCamera::Update의 구현을 보여준다. 먼저 해당 프레임에 적용되는 요의 양을 나타내는 쿼터니언을 선언한다. 이 쿼터니언은 세계의 상향 벡터에 대한 쿼터니언이다. 이 쿼터니언을 사용해서 카메라의 오프셋과 상향 벡터를 변환한다. 다음으로 새 오프셋으로부터 카메라의 전방 벡터를 계산한다. 카메라의 전방 벡터와 카메라의 상향 벡터와의 외적을 통해 카메라의 오른쪽 벡터를 구한다. 그런 다음 이 카메라의 오른쪽 벡터를 사용해서 피치 쿼터니언을 계산하고 이 쿼터니언을 사용해서 카메라 오프셋과 상향 벡터를 회전 시킨다. look-at 행렬의 경우 카메라의 타겟 위치는 단순히 소유자의 위치이며 카메라 위치는 소유자의 위치+오프셋이다. 그리고 상향 벡터는 카메라의 상향 벡터이다.

스플라인 카메라
스플라인(spline)은 곡선상의 일련의 점들로 구성된 곡선을 수학적으로 표현한 것이다. 스플라인은 게임에서 인기가 많다. 왜냐하면 스플라인은 오브젝트가 일정 기간동안 곡선을 따라 부드럽게 움직일 수 있게 해주기 때문이다. 카메라가 미리 정의된 스플라인 경로로 따라갈 수 있으므로 스플라인은 컷신(cutscene) 카메라에 매우 유용하다. 게임에서 카메라가 플레이어가 세계를 나아갈 때 설정된 경로를 따라 이동하는 것이 예가 될 수 있다. 캣멀롬(catmull-rom) 슾플라인은 상대적으로 계산하기 간단한 스플라인 타입이라서 게임과 컴퓨터 그래픽스에서 자주 사용된다. 이런 유형의 스플라인에서는 부터 까지 4개의 제어점을 요구한다. 실제 곡선은 에서 까지이며 는 곡선이 시작되기 전의 제어점에 해당하며 은 곡선이 끝난 후의 제어점에 해당한다. 최상의 결과를 얻으려면 이러한 제어점을 곡선상에 균둥하게 배치해야한다. 곡선상의 균등하게 배치하기위해서 유클리드 거리를 사용한다.

위 그림은 4개의 제어점을 가진 캣멀롬 곡선을 보여준다. 이 4가지 제어점이 주어지면 다음 매개변수 방정식처럼 , 사이의 점을 표현할 수 있다. 여기서 일때는 이며 일때는 다.
캣멀롬 스플라인 방정식은 오직 4개의 제어점만 있지만, 임의의 수의 제어점으로 스플라인을 확장하는 것도 가능하다. 이 확장된 스플라인은 제어점들이 경로점이 되거나 아닐수 있으며 경로 앞에 한 점 그리고 경로 뒤에 한 점이 여전히 존재하므로 잘 동작한다. 다시 말하자면 개의 점을 가진 곡선을 나타내는 데는 개의 점이 필요하며 개발자는 4개의 인접한 점을 얻은 뒤 이 4개의 점들로 구성된 스플라인 방정식을 사용하면 된다. 스플라인 경로를 따르는 카메라를 구현하려면 스플라인을 정의하는 구조체를 정의해야한다. Spline이 필요로하는 유일한 멤버 데이터는 제어점을 담는 벡터이다.
struct Spline
{
// 스플라인에 대한 제어점
// (세그먼트상에 n개의 점이 있다면 총 n + 2개의 점이 필요하다)
std::vector<Vector3> mControlPoints;
// startIdx = P1인 스플라인 세그먼트가 주어졌을 때
// t 값을 토대로 위치를 계산한다.
Vector3 Compute(size_t startIdx, float t) const;
size_t GetNumPoints() const { return mControlPoints.size(); }
};Spline::Compute 함수는 에 해당하는 시작인덱스와 [0.0, 1.0] 범위에 있는 t 값을 스플라인 방정식에 적용한다.

위 코드에서 보여주듯이 이 함수는 startIdx가 유요한지 검증하기 위해 경계값을 확인한다. 그리고 SlpineCamera 클래스에 멤버 테이더로 Spline을 추가한다. 또한 SplineCamera에 에 해당하는 현재 인덱스, 현재 의 값, 속도, 카메라가 경로를 따라 이동해야하는지 여부를 결정하는 플래그 값을 기록한다.
// 카메라가 따라가는 스플라인 경로
Spline mPath;
// 현재 제어점 인덱스 및 t
size_t mIndex;
float mT;
// 초당 t의 변화율
float mSpeed;
// 경로를 따라 카메라가 이동해야 하는지의 여부
bool mPaused;스플라인 카메라는 먼저 속도와 델타 시간의 함수로 t값을 증가시켜 갱신한다. t값이 1.0보다 크거나 같으면 은 경로상의 다음 점으로 이동한다(경로상에 충분한 점이 있다고 가정한다). 이 이동한다는 것은 또한 값에서 1을 빼야한다는 것을 의미한다. 스플라인에 더 이상 점이 존재하지 않는다면 스플라인 카메라는 멈춘다. 카메라 계산에서 카메라의 위치는 단순히 스플라인으로부터 계산된 점이다. 대상 지점을 계산하려면 스플라인 카메라가 이동하는 방향을 결정하기 위해 작은 델타값으로 를 증가시켜야한다. 마지막으로 상향 벡터는 스플라인이 거꾸로 뒤집혀지지 않는다는 것을 가정해서 (0, 0, 1)로 유지한다.


언프로젝션
세계 공간의 점을 클립 공간으로 변환하기 위해서느느 먼저 뷰 행렬을 투영 행렬과 곱해야한다. 그런데 1인칭 슈팅 게임에서 플레이어가 조준점의 화면 위치를 토대로 발사체를 쏜다고 가정해보자. 이 경우 조준점의 위치는 화면 공산상의 좌표다. 하지만 올바르게 발사체를 쏘려면 세계 공간ㄴ에서의 조준점 위치가 필요하다. 언프로젝션(unprojection)은 화면 공간 좌표로부터 세계 공간 좌표로 변환하는 계산이다. 해상도 인 윈도우 창에서 화면 공간 좌표 체계에서는 화면의 중심이 (0, 0)이고, 왼쪽 상단이 (-512, 384)였고 오른쪽 하단이 (512, -384)였다. 언프로젝션을 계산하는 첫번째 단계는 화면 공간의 x, y 요소를 [-1, 1]의 범위값을 가진 정규화된 장치 좌표로 변환하는 것이다.
그러나 여기에는 문제점이 있는데 하나의 (x, y)좌표는 [0, 1]의 범위를 가지는 z 좌표도 가진다. z값이 0이면 가까운 평면의 점을 의미하고(카메라의 바로 앞에 있는) z값이 1이면 먼 평면의 점이다(카메라를 통해서 볼 수 있는 최대 거리). 그래서 언프로젝션을 올바르게 수행하기 위해서는 범위 [0, 1]의 z 요소값이 필요하다. 그리고 좌표는 동차 좌표로 나타낸다.
이제 언프로젝션 행렬을 생성한다. 언프로젝션 행렬은 뷰 투영 행렬의 역행렬이다.
언프로젝션 행렬을 NDC에 곱하면 w 요소값이 변경된다. 그래서 각 요소값을 w로 나눠서 w요소를 1로 되돌릴 수 있도록 재정규화가 필요하다. 이를 위해 다음 계산식이 필요하며그 결과 세계 공간의 점을 얻게 된다.
Renderer 클래스는 뷰 행렬과 투영 행렬 모두에 접근할 수 있는 유일한 클래스이므로 Renderer 클래스에 언프로젝션에 대한 함수를 추가한다.

위 코드는 Unproject 함수 구현을 보여준다. 이 코드에서 TransformWithPerspDiv 함수는 언프로젝션 행렬과 w 요소를 사용해서 재정규화를 수행한다. 이제 Unproject를 사용하면 세계 공간상의 위치 계산이 가능하다. 그리고 이 함수를 활용해서 화면 공간 점으로 향하는 벡터를 만들어두면 다른 유용한 기능을 활용할 수 있는 기회를 얻을 수 있다. 그런 기능 중 하나는 피킹(picking)이다. 피킹은 3D 세계상에서 오브젝트를 클릭해서 선택할 수 있게 하는 기능이다.

위 그림은 마우스 커서로 피킹하는 모습을 보여준다. 방향 벡터를 만들려면 Unproject를 두 번 사용해야한다. 시작점에서 한 번 사용하고 끝 점에서 한 번 사용한다. 그런 다음 벡터 간의 뺄셈을 한 후에 이 벡터를 정규화한다.

위 코드는 위 과정을 Renderer::GetScreenDirection 함수에 구현한 것이다.


