Day 20 충돌 감지의 기본
기하 타입
게임을 위한 충돌 감지에서는 기하나 선형대수 같은 여러 다양한 개념을 활용한다. 게임에서 사용되는 일반적인 기하 타입으로는 선분, 평면, 박스 등이 있다.
선분
선분(line segment)은 시작 지점과 끝 지점으로 구성된다.
struct LineSegment
{
Vector3 mStart;
Vector3 mEnd;
}선분상의 임의의 점을 계산하려면 다음 매개 방정식을 사용하면 되는데, 와 는 각각 시작 지점과 끝 지점이고 는 파라미터다. 편의성을 위해 t 값이 주어졌을 때 선분상의 한 점을 반환하는 멤버 함수를 LineSegment 클래스에 추가한다.
Vector3 LineSegment::PointOnSegmen(float t) const {
return mStart + (mEnd - mStart) *t;
}선분의 매개 표현식은 손쉽게 광선이나 선의 정의로 확장할 수 있다. 광선은 위의 방정식을 따르지만 t값의 경계는 다음과 같다.
마찬가지로 직선은 값에 경계가 없다.
선분과 광선은 여러 다양한 유형의 충돌 감지를 위한 쓰임새가 많은 기본 기하 타입이다. 예를 들어 게임에서 직선으로 총알을 발사하거나 땅에 착지하는 경우 선분을 사용한다. 또한 조준용 십자선을 위해 선분을 사용하며 소리 차폐 테스트, 마우스 피킹에도 사용한다. 또 다른 유용한 연산은 임의의 한 점과 선분 사이의 최소 거리를 찾는 것이다. 선분이 점 A에서 시작하고 B에서 끝난다고 하면 임의의 점 C가 주어졌을 때 선분과 점 C 사이의 최소 거리를 구하려면 아래 그림 처럼 3가지의 다른 경우를 고려해야한다.

위 그림에서 (a)와 같은 경우 와 사이의 각이 90보다 크다. 내적을 사용하면 90보다 큰지를 확인하는 것이 가능하다. 내적이 음수이면 두 벡터 사이의 각이 둔각임을 의미하므로 C와 선분 사이의 최소 거리는 벡터 의 길이가 된다. 그림 (b)에서의 경우는 와 사이의 각이 90보다 크다. 첫 번째 경우 처럼 내정으로 이 상황을 테스트할 수 있다. 이 경우에 최소 거리는 의 길이가 된다. 그림 (c)의 경우는 와 에 수직하는 로의 선분을 그린다. 이 새 선분의 길이는 와 사이의 최소 거리다. 이 선분을 구하려면 먼저 벡터 를 계산해야한다. 의 방향은 정규화된 와 같은 방향이므로 이미 알고 있다. 여기서는 스칼라 투영(scalar projection)이라는 내적의 특성을 사용해서 를 구한다. 스칼라 투영은 직교 투영을 의미하며 이 예시에서는 선분 를 선분 로 직교 투영하는 것을 뜻한다. 비단위 벡터 는 직각 삼각형을 구성하기 위해 확장되거나 축소되어야한다. 즉 선분 가 선분 로 직교 투영된, 벡터 의 길이는 와 정규화된 (즉 의 단위 벡터)의 내적이된다.
결국 벡터는 는 정규화된 벡터와 의 길이의 스칼라 곱이 된다.
벡터의 제곱 길이와 내적은 같다는 걸 기억하고 몇가지 대수적 계산을 사용하면 는 다음과 같이 간소화된다.
마지막으로 에서 로의 벡터를 선언한다. 이 벡터의 길이는 와 까지의 최소 거리다.
거리는 양수 값이며 에서 까지의 최소 거리의 제곱값을 얻기 위해 방정식 양쪽을 제곱한다.
이렇게 하면 비용이 큰 제곱근 연산을 피할 수 있다.
LineSegment::MinDistSq

평면
선분이 무한히 확장되는 1차원 오브젝트인 것처럼, 평면(plane)은 무한히 확장되는 평평한 2차원 표면이다. 게임에서는 평면을 땅이나 벽면을 추상화한 형태로 표현한다. 평면의 방정식은 다음과 같다.
는 평면상의 임의의 점이고 평면에 수직하는 법선 벡터다. 그리고 는 평면과 원점 사이의 부호 있는 최소 거리값이다. 게임 코드는 일반적으로 점이 해당 평면상에 놓여있는지를 자주 확인한다(즉, 점이 평면상에 있다면 평면의 방정식을 만족한다). 평면을 표현하기 위한 plane 구조체의 정의는 법선 벡터와 값만으로 충분하다.
struct Plane
{
Vector2 mNormal;
float mD;
};정의상 삼각형은 단일 평면에 놓인다. 그래서 삼각형이 주어지면 평면의 방정식 유도가 가능하다. 삼각형을 구성하는 버텍스로 2개의 벡터를 만들고, 이 두 벡터로 외적을 하면 삼각형의 법선을 얻는데 이 법선은 평면의 법선과 같다. 평면의 임의의 한 점은 알고 있으므로(삼각형의 버텍스 중 하나) 이 버텍스와 점으로 의 값을 구할 수 있다.

임의의 점 와 평면 사이의 최소 거리를 구하는 것은 선분에서 했던 작업과 유사하다(선분은 내적의 스칼라 투영 특성을 사용했다). 아래 그림은 평면을 측면에서 바라보면서 계산하는 과정이다.

평면 의 법선 벡터를 알고 있고 원점과 평면 사이의 거리 도 알고 있으므로 먼저 와 법선 의 내적을 통해서 스칼라 투영을 계산한다.
그리고 값에 이 스칼라 투영값을 빼면 그 결과는 C와 평면 간 부호 있는 거리 가차 된다.
음수값은 가 평면 아래에 있다는 걸 의미하고(법선의 반대방향), 양수는 가 평면 위에 있음을 의미한다. 부호 있는 거리 계산의 코드 구현은 다음과 같다.

바운딩 볼륨
현대 3D 게임은 수천 개의 삼각형으로 구성된 캐릭터와 오브젝트로 표현된다. 두 오브젝트의 충돌 여부를 결정하고자 할 때 오브젝트를 구성하는 모든 삼각형의 교차 여부를 테스트하는 것은 효율적이지 못하다. 이런 이유로 게임에서는 박스나 구체같은 간소화된 바운딩 볼륨(bounding volume)을 사용한다. 두 오브젝트의 교차 판단을 위한 단순화된 충돌 계산을 통해 게임은 매우 향상된 효율성을 얻는다.
구체
3D 오부브젝트의 가장 단순화된 경계 표현은 구체(sphere)다. 구체의 정의에 필요한 것은 구체의 중심과 반지름 뿐이다.
struct Sphere
{
Vector3 mCenter;
float mRadius;
};
위 그림에서 볼 수 있듯이 바운딩 구체는 일부 오브젝트에는 적합하지만, 다른 오브젝트에는 적합하지 않다. 예를 들어 인간형 캐릭터 주위를 감싼 바운딩 구체는 캐릭터와 구체 경계 사이에 빈 공간이 많다. 물체에 대한 경계 부분이 헐렁하므로 두 물체의 바운딩 볼륨이 교차한다 하더라도 실제로는 충돌하지 않았음을 의미하는 긍정 오류(positive error)가 발생한다. 예를 들어 1인칭 슈터 게임에서 인간형 캐릭터에 바운딩 구체를 사용했다면 플레이어는 캐릭터의 왼쪽이나 오른쪽으로 탄환을 쐈는데 맞지 않았음에도 게임은 맞았다고 판정할 수 있다. 그러나 바운딩 구체를 사용하면 교차 계산이 매우 효율적이라는 이점을 가진다. 게다가 회전은 구체에 영향을 주지 않으므로 바운딩 구체는 3D 오브젝트의 회전에 상관없이 잘 동작한다. 그리고 공과 같은 일부 오브젝트에서 구체는 경계를 완벽하게 표현한다.
축 정렬 바운딩 박스
2D에서 축 정렬 바운딩 박스(AABB, Axis-Aligned Bounding Box)는 모서리가 x축과 y축에 평행한 삭가형이다. 비슷하게 3D에서 AABB는 프리즘의 모든 명이 좌표축 평면의 하나와 평행한 사각형 프리즘이다. AABB는 최소점과 최대점 두 점으로 정의한다. 2D상에서 최소점은 왼쪽 하단 점이며, 최대점은 오른쪽 상단 점과 일치한다. 다시 말해서 최소점은 박스상에서 최소값 x,y 의미하며, 최대점은 박스 상에서 x,y 최대값을 의미한다. 마찬가지로 3D 상에서도 최소점은 박스상에서 x,y,z 최소값을 가지며, 최대점은 x,y,z 최대값을 갖는다. 구조체로 바꿔보면 다음과 같다.
struct AABB
{
Vector3 mMin;
Vector3 mMax;
};AABB는 여러 점들을 이용하면 쉽게 생성할 수 있다. 예를 들어 모델을 로딩하는 경우 일련의 버텍스를 얻을 수 있고, 이 버텍스 시퀀스를 모델에 대한 AABB를 정의하는데 사용할 수 있다. 이를 위해 점을 파라미터로 받는 UpdateMinMax 함수를 구현한다. UpdateMinMax 함수는 이 점에 따라 min, max를 갱신한다.

새로운 점이 모든 다른 점에 대해 상대적으로 어디에 위치하는지를 알 수 없으므로 min, max 값을 갱신하려면 모든 요소를 개별적으로 테스트해야한다. 그런 다음 점 리스트를 가진 컨테이너가 주어지면 먼저 컨테이너의 첫 번째 점값으로 AABB의 min, max를 초기화한다. 첫 번째 점을 제외한 나머지 점들에 대해서는 단순히 UpdateMinMax 함수를 호출한다.
// points는 std::vector<Vector3> 타입
AABB box(points[0], points[0]);
for (size_t i = 1; i < points.size(); i++) {
box.UpdateMinMax(points[i]);
}AABB 대신 좌표 평면과 평행을 유지해야하므로 물체의 회전은 AABB를 회전시키지 않고 대신 AABB의 면적을 변경한다. 아래의 그림은 그 예시이다.

일부 경우에서는 AABB 회전을 계산할 필요가 없을 수도 있다. 예를 들어 게임상에서 대부분의 인간형 캐릭터는 오직 상향축만을 기준으로 회전한다. 따라서 캐릭터의 AABB를 충분히 넓게 만들면 캐릭터가 회전해도 AABB는 변경할 필요가 없다. 그러나 다른 오브젝트에는 회전에 대한 AABB를 계산하는 것이 필요하다. 오브젝트 회전 후 AABB를 계산하는 한 가지 방법은 먼저 AABB의 구석을 나타내는 8개의 점을 생성하는 것이다. 이 점들은 단순히 min max 요소로 표현한 점들의 나열이다. 그런 다음 오브젝트의 각 점을 회전시킨 뒤 회전된 점으부터 새로운 AABB를 생성하기 위해 UpdateMinMax를 사용한다. 이 과정은 아래 코드에서 볼 수 있듯 회전 후에 해당 오브젝트의 가장 작은 AABB는 계산하지 않는다. 그러므로 게임은 여러 번의 회전 후에 에러를 전파히지 않기 위해 원래 물체의 AABB를 저장해야한다.

방향성 있는 바운딩 박스
방향성이 있는 바운딩 박스(OBB, Oriented Bounding Box)는 AABB처럼 축이나 평면에 대해 평행해야 한다는 제한이 없다, 그렇게 때문에 아래 그림처럼 물체에 딱 맞는 경곗값을 유지한다.

OBB를 표현하는 한 가지 방법은 중심점과 회전을 위한 쿼터니언, 그리고 박스를 위한 값들(너비, 높이, 깊이)를 갖는 것이다.
struct OBB
{
Vector3 mCenter;
Quarternion mRotation;
Vector3 mExtents;
};OBB를 사용하면 충돌 계산량이 AABB보다 너무 비싸다,
캡슐
캡슐(capsule)은 반지름을 가진 선분이다.
struct capsule
{
LineSegment mSegment;
float mRadius;
};
위 그림처럼 캡슐은 인간형 캐릭터를 나타내는 데 나타내는 데 자주 사용된다. 캡슐은 또한 구체가 움직인 영역이다. 왜냐하면 구체가 이동할 때는 시작점ㄷ과 끝점이 있고, 이동 중의 구체는 반경을 가지고 있기 때문이다.
볼록 다각형
때론 게임은 기본 형태보다 더 정확한 물체의 경계를 필요로 한다. 2D 게임에서는 물체의 바운딩 볼륨을 볼록 다각형(convex polygon)으로 표현하는 것이 가능하다. 내부의 모든 각이 180보다 작다면 그 다각형은 볼록 다각형이다. 볼록 다각형은 버텍스의 컬렉션으로 표현 가능하다.
struct ConvexPolygon
{
// 버텍스는 시계 방향으로 정렬돼 있다.
std::vector<Vector2> vectices;
};이 버텍스들은 다각형의 모서리를 따라 시계 방향순, 또는 반시계 방향순으로 정렬돼야한다. 정렬이 안돼 있다면 오브젝트 간 교차 확인은 계산이 매우 어렵다. 다각형이 볼록 다각형이고 시계 방향 순으로 버텍스가 정렬돼 있는지를 검증하는 테스트가 없으므로 볼록 다각형 구조체는 개발자가 올바르게 사용한다고 가정한다.
교차 테스트
게임은 게임 오브젝트의 충돌을 표현하기 위해 여러가지 도형을 사용한다. 그리고 그 오브젝트들 간의 교차 여부를 테스트한다. 먼저 오브젝트가 점을 포함하는지 판정하는 방법을 알아보고 다음으로 여러 타입의 바운딩 볼륨 간 교차를 알아본다. 마지막으로는 동적으로 움직이는 오브젝트를 다루는 방법을 알아본다.
점을 포함하는지 판정하는 테스트
물체가 특정한 점을 포함하는지 여부를 테스트하는 것은 그 자체로 매우 유용하다. 예를 들어 플레이어가 게임 세계의 특정 지역 내부에 있는지 여부를 판단하는 테스트에 이런 형태의 테스트를 사용할 수 있다. 또한 일부 물체의 교차 알고리즘은 물체에 근접한 점을 찾고, 그 점이 물체 내부에 있는지를 알아내는데 의존한다.
구의 점 포함 판정 테스트
구가 점을 포함하는지를 알아내기 위해 먼저 점과 구의 중심사이의 거리를 구한다. 이 거리가 구의 반지름보다 같거나 작다면 구는 점을 포함한다. 거리와 반지름은 둘 다 양수이므로 제곱한 값을 사용해도 비교연산은 항등성을 유지한다. 제곱근 연산을 피하고 하나의 곱셈만을 포함해서 비용이 큰 제곱근 연산을 피한다.

AABB 점 포함 판정 테스트
2D AABB에 대해서 점은 다음과 같은 경우가 참이면 박스 바깥에 있다.
- 점이 박스 왼쪽에 있다
- 점이 박스 오른쪽에 있다
- 점이 박스 위쪽에 있다
- 점이 박스 아래쪽에 있다
이 경우에 해당하지 않으면 박스는 점을 포함해야한다. 이 테스트는 박스의 min, max 점과 박스 내부에 존재하는지를 확인할 점의 요소를 단순히 비교하기만 하면된다. 예를 들어 x 요소가 min.x보다 작다면 점은 박스의 왼쪽에 있다. 이 개념은 3D AABB에도 쉽게 확장할 수 있다. 하지만 2D 박스는 네 번의 측면검사가 필요한 반면 3D AABB에서는 6개의 면이 존재하므로 여섯 번의 검사가 필요하다.

캡슐의 점 포함 테스트
캡슐이 점을 포함하는지 유무를 테스트하려면 먼저 점과 선분 사이의 최소 거리 제곱값을 계산해야한다. 최소 거리 제곱값을 계산하기 위해 LineSegment::MinDistSq 함수를 사용한다. 최소 거리 제곱값이 반지름 제곱값보다 같거나 작으면 캡슐은 점을 포함한다.

볼록 다각형의 점 포함(2D) 테스트
2D 다각형을 포함하는지를 테스트하는 방법에는 여러 가지 방법이 존재한다. 가장 간단한 접근법 중 한 가지는 각 버텍스 간 벡터를 만드는 것이다. 그리고 인접한 두 벡터 간 내적을 한 뒤 이 두 벡터가 이루는 각을 구하는 아크코사인 계산을 한다. 이 각들의 모든 합이 360에 가까우면 점은 폴리곤 내부에 있는 것이다. 그렇지 않으면 점은 폴리곤 바깥에 있다.


이 유형의 테스트 코드는 두 인접한 버텍스는 볼록 다각형 벡터에서도 인접한 인덱스를 가져야한다. 하지만 이 각의 총합 접근법은 그렇게 효율적이지 못하다. 왜냐하면 이 접근법은 제곱근과 아크코사인 계산을 요구하기 때문이다. 보다 복잡하지만 다른 접근접 중에는 위 접근법보다 효율적인게 많다. 그 중 한 가지는 점에서 시작하는 무한한 광선을 그리고 그 광선이 모서리와 몇 개나 교차하는지를 세는 것이다. 광선이 모사리와 홀수로 교차한다면 점은 폴리곤 내부에 있다. 그렇지 않으면 점은 바깥에 있다. 이 광선 접근법은 볼록 다각형 뿐만 아니라 오목 다각형에서도 잘 동작한다.
바운딩 볼륨 테스트
여러 바운딩 볼륨 간 교차 테스트 계산은 매우 일반적이다. 예를 들어 플레이어와 벽의 충돌 검사를 위해 둘 다 AABB를 사용한다고 가정하면 플레이어가 앞으로 이동할 때 플레이어의 바운딩 볼륨이 벽의 바운딩 볼륨과 교차하는지 테스트한다. 그리고 플레이어와 벽이 교차한다면 플레이어의 위치를 더 이상 교차하지 않도록 수정한다.
구체와 구체 교차 테스트
두 구체는 구체의 중심 사이의 거리가 각 구체의 반지름 합보다 작거나 같으면 교차한다. 구체의 점 포함 테스트처럼 효율성을 위해 양변을 제곱해도 항등성이 유지된다는 것을 활용한다.

AABB와 AABB의 교차 테스트
AABB 교차를 시험하는 로직은 AABB가 점을 포함하는지 판단하는 로직과 같다. 두 AABB가 교차할 수 없는 경우를 테스트해본다. 이 테스트가 모두 참이 아니면 두 AABB는 교차해야한다. 2D AABB 에서 박스 A,B는 A가 B의 왼쪽 아래 있거나 A가 B의 오른쪽에 있거나 A가 B의 위에 있는 경우 또는 A가 B의 아래에 있으면 교차하지 않는다. 이 테스트는 이전에 보여줬듯이 min과 max 점을 사용하면 된다. 예를 들어 A는 A의 max.x가 B의 min.x보다 작으면 B의 왼쪽에 있다. 아래 그림은 2D AABB의 교차 테스트를 잘 보여준다.

2D AABB의 교차 테스트를 3D AABB 교차 테스트로 변경할 때는 6개의 요소를 다루기 위해 2가지 검사를 더 추가한다.

이러한 형태의 AABB 교차는 두 볼록한 오브젝트가 교차하지 않으면 A와 B를 구분하는 축이 존재해야 함을 나타내는 분리 축 이론(separating axis theorem)을 적용한 것이다. AABB의 경우에서는 3개의 축으로 박스 사이에 분리가 있는지를 테스트하고 있다. AABB가 특정 축으로 분리가 된다면 분리 축 정리에 따라 두 박스는 교차할 수 없다. 이러한 접근법은 모든 볼록한 오브젝트에 적용 가능하다.
구와 AABB 교차 테스트
구와 AABB 교차 테스트를 하려면 먼저 구의 중심과 박스 사이의 최소 거리 제곱값을 계산해야한다. 점과 AABB 사이의 최소 거리를 찾는 알고리즘은 각 요소를 개별적으로 테스트해야한다. 3가지 테스트 경우의 수가 존재한다.
- 점의 요소가 min보다 작다
- 점의 요소가 min, max 사이에 있다
- 점의 요소가 max보다 크다
두 번째 경우 점과 박스 사이의 거리는 0이다. 다른 2가지의 경우 점과 박스 사이의 거리는 가장 가까운 모서리와의 거리다. Math::Max 함수를 여러 번 호출해서 거리를 구하자. 예를 들어 x 방향에서는 거리는 다음과 같다.
float dx = Math::Max(mMin.x - point.x, 0.0f);
dx = Math::Max(dx, point.x - mMax.x);위의 코드는 point.x < min.x이면 min.x - point.x는 세값 중에서 가장 크며, x축에 대한 델타 값이 된다. 그렇지 않고 min.x < point.x < max.x라면 0이 가장 크다. 마지막으로 point.x - max.x라면 point.x - max.x가 가장 크다. 세 축 모두에 대한 델타를 얻으면 점과 AABB 사이의 최종 거리 제곱값을 계산하는 거리 공식을 사용한다.

MinDistSq 함수 구현으로 이제 구체와 AABB 간 교차 테스트가 가능해졌다. 구체의 중심과 AABB의 최소 거리 제곱을 알아내고 그 값이 반지름의 제곱보다 작거나 같다면 구와 AABB는 교차한다.

캡슐과 캡슐 교차 테스트
두 캡슐의 교차 테스트는 개념적으로 간단하다. 캡슐은 반경이 있는 선분이므로 먼저 이 선분 사이의 최소 거리 제곱값을 구한다. 최소 거리 제곱값이 선분들의 반경의 합 제곱보다 작거나 같다면 두 캡슐은 교차한다.

두 선분 사이의 최소 거리를 계산하는 것은 몇몇 가장자리 경우 때문에 복잡하다.
선분 테스트
선분은 충돌 감지에서 다양하게 활용된다. 선분과 다른 오브젝트간의 몇 가지 핵심 테스트가 있다. 이 테스트는 선분이 교차하는지 여부뿐만 아니라 최초로 교차되는 점을 알아내는 것도 포함한다. 이 때 이전에 정의했던 선분 매개 방정식을 사용한다.
대부분의 선분 교ㅕ차 테스트 접근법은 선분을 무한히 긴 선으로 다룬다. 왜냐하면 무한한 선이 오브젝트와 교차하지 않으면 당연히 선분도 물체와 교차하지 않기 떄문이다. 무한히 긴 선과 오브젝트가 교차한다면 값이 [0, 1] 경계 내의 값인지를 확인해 선분ㄱ돠 오브젝트의 충돌을 최종 검증한다.
선분과 평면의 교차 테스트
선분과 편면의 교차점을 찾으면 점 가 평면 상에 위치하게 하는 를 찾아야한다.
위 평면의 방정식에서 를 치환한다.
마지막으로 위 식을 정리한다.
분모의 내적이 0이 된다면 나눗셈이 안되는데, 이 경우는 선이 평면의 법선과 수직일 경우이며 선이 평면과 평행하다는 것을 의미한다. 이 경우는 선이 평면상에 있을 경우만 교차한다. 값을 계산한 후에는 가 선분의 경계 내에 있는지 테스트한다.

이 Intersect 함수는 참조로 값을 반환하는데 호출자는 이것을 이용해 선분과 평면의 교차점이 필요할때 값을 활용한다.
선분과 구체의 교차 테스트
선분과 구 사이의 교차점을 찾기 위해 먼저 선과 구체 사이에 거리가 구의 반지름 과 같은 가 있는지 찾는다.
위 방정식을 간단하게 하기 위해 변수를 치환한다.
를 구하려면 길이 연산 내부에서 를 꺼낼 방법이 필요하다. 이를 위해 방정식 양쪽을 제곱하고 길이의 제곱을 내적 형태로 대체한다.
내적은 벡터 덧셈에 대해 분배 법칙이 가능하므로 분배 법칙을 적용한다.
그 다음 이 식을 t의 이차방정식 형태로 정리한다.
마지막으로 t에 대한 이차방정식의 근을 정리한다.
이 이차방정식의 판별식을 통해 방정식의 해의 개수와 유형을 알 수 있다. 판별식이 음수라면 해는 허수이다. 게임에는 목적상 물체의 허수 위치가 존재하지 않는다. 그러므로 음수 판별식은 선이 구체와 교차하지 않는다는 걸 의미한다. 음수 판별식을 제외하면 이차방정식의 해는 1개나 2개가 존재한다. 판별식이 0이라면 선이 구에 접하므로 1개의 해가 있다는 걸 의미한다. 판별식이 0보다 크면 구체와 교차하는 점이 2개 있다.
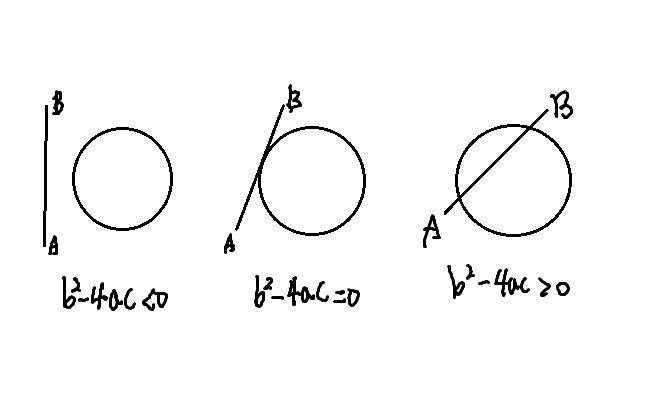
그리고 의 해를 구했으면 가 [0, 1] 범위 내부의 값인지 검증한다. 는 2개의 해가 존재할 수 있기에 최초의 교차를 나타내는 작은 값을 고른다. 하지만 선분이 구의 내부에서 시작한다면 큰 의 값이 교차점이이다. 아래 코트는 선분과 구체의 교차 테스트 코드이다. 함수는 구체가 선분 전체를 포함하면 false를 반환한다.

선분과 AABB 테스트
선분과 AABB 교차 테스트 방법 중 하나는 박스의 각 가장자리에 평면을 만드는 것이다. 2D에서는 4개의 가장자리에 4개의 평면을 만들 수 있다. 평면은 무한하므로 가장자리 평면과 선분이 교차한다고 해서 선분이 박스와 교차한다는 걸 의미하지는 않는다.

위 그림의 (a)처럼 선분은 이 위쪽 모서리 평면과 교차하고 가 왼쪽 모서리 평면과 교차하지만 박스가 이 점들을 포함하고 있지 않으므로 이 선분은 박스와 교차하지 않는다. 하지만 그림 (b)는 선분은 왼쪽 모서리 평면 와 교차하는데 박스가 를 포함하므로 이 점은 교차점이다. 선분은 그림 (C)처럼 복수의 교차점을 가질 수 있다. 와 둘 다 박스와 교차한다. 이경우에 교차는시작점과 가까운 점을 반환하거나 선분 매개 방정식에서 작은 값을 가지는 점을 반환해야한다. 선분과 평면 교차에 대한 방정식은 아래와 같았다.
여기서 각각의 평면은 좌표축과 평행하므로(3D에서는 좌표 평면에) 각 평면의 법선은 쉽게 구할수 있다. 특히 3D에 경우에 2개의 요소가 항상 0이고 한 요소만이 1이므로 위의 식은 간단하게 최적화된다. 즉 3개의 내적 요소중 2개는 항상 0이라는 뜻이다. 예를 들어 2D 상에서 왼쪽 모서리 평면은 왼쪽이나 오른쪽을 가리킨다. 2D에서 방향은 교차에 한해서는 중요하지 않다. 따라서 법선 벡터는 다음과 같다.
박스의 min 점은 왼쪽 모서리에 평면에 있으므로 값은 다음과 같다.
마찬가지로 선분과 평면의 교차 방정식에서 내적은 x요소만으로 간소화된다. 즉, 왼쪽 모서리 평면에 대한 교차점의 해를 구하는 최종 방정식은 다음과 같다.
다른 평면의 방정식도 비슷하게 유도되는데 3D에서는 테스트해야 될 평면이 총 6개다. 그래서 하나의 평면을 테스트하기 위한 작업을 캡슐화한 헬퍼 함수가 필요하다. 이 함수는 선분이 평면과 교차하면 값을 std::vector에 추가하고 교차 함수는 이 std::vector를 사용해 모든 가능한 값을 순서대로 테스트한다.

그리고 이제 선분과 AABB의 교차를 테스트하는 Intersect 함수는 선분과 AABB 6개 평면과의 교차 여부를 시험하기 위해 TestSidePlane 함수를 사용한다. Intersect함수는 평면과 교차하는 각각의 점 t를 tValues 벡터에 저장하고, 오름차순으로 이 벡터를 정렬한 뒤 AABB에 포함되는 최조의 교차점을 반환한다. AABB가 교차점을 하나도 가지지 않는다면 false를 반환한다.

박스의 각 측면을 독립적으로 테스트하므로 어떤 평면이 선분과 교차하는지 반환하도록 교차 함수를 수정하는 것이 가능하다. 이렇게 수정하면 물체가 상자 바깥으로 튀어나와야 하는 경우에 유용하다. 그렇게 하려면 TestSidePlane 각각의 호출을 박스의 측면과 연관지어야한다. 그런 다음 교차한 측면을 Intersect 함수가 얻도록 참조 파라미터를 추가하면 된다. 두 평면으로 묶인 무한한 평판(slabs)을 사용하면 AABB 교차는 좀 더 최적화가 가능해진다.
동적 오브젝트
지금까지 살펴본 교차 테스트는 동시에 일어나는 사건의 테스트였다. 이는 게임에서 두 물체가 현재 프레임에서 교차하는지 여부를 테스트한다는 것이다. 이러한 테스트는 간단한 게임에 한해서는 충분할 수 있지만 현실적으로 문제점이 많다. 캐릭터가 종이로 탄환을 발사하는 경우를 가정해보자. 탄환은 바운딩 구체를 사용하고 종이는 바운딩 박스를 사용한다. 각 프레임에서는 탄환과 종이가 정확히 교차하는 특정한 하나의 프레임이 존재할 가능성은 거의 없다. 즉 교차의 즉석 테스트는 아래의 그림 처럼 교차 상황을 놓칠 수 있다.

탄환과 같은 특정한 경우에는 탄환을 선분으로 다룸으로써 교차 문제를 해결하는 것이 가능하다. 선분의 시작점은 이전 프레임의 탄환 위치이고 끝점은 현태 프레임의 탄환 위치이다. 이렇게 하면 이전 프레임과 현제 프레임 사이의 특정 지점에서 탄환과 종이의 교차를 감지하는 것이 가능해진다. 그러나 이 방법은 탄환이 매우 작을 경우에만 동작한다. 커다란 물체는 선분으로 표현할 수 없다. 이동 중인 구체 2개의 충돌같은 일부 유형의 오브젝트 충돌은 교차시간에 바로 정확한 충돌을 알아내는 것이 가능하다.하지만 2프레임에 걸쳐 회전하는 박스의 경우에는 충돌이 정확한지 파악하는 것은 러협다. 여러 유형의 이동 오브젝트(물체)에 대해 프레임 사이의 여러 지점에서 충돌 여부를 판별하는 과정을 연속 충돌 감지(CCD, Continuous Collision Detection)이라고 한다. 교차 지젬에 바로 충돌을 알아내는 방법을 가볍게 알아보기 위해 이동 중인 두 구체 사이의 교차를 알아보자. 이를 구의 궤적 교차(swept-sphere Intersection)라고 부른다.

각가의 구체에 대해 이전 프레임과 현재 프레임의 중심점을 알고 있다. 구의 중심점을 선분의 매개 방정식으로 나타내면 이전 프레임의 중심점은 일 때이며, 현재 프레임의 중심점은 일 때다. 구체 에서 는 이전 프레임 위치이고 은 현재 프레임의 위치이다. 똑같이 구체 는 , 을 갖는다. 그래서 두 구체 와 는 위쳉 대한 매개 방정식을 다음처럼 기술할 수 있다.
그리고 두 구체 사이의 거리가 두 구체 반지름의 합과 같을 때의 값이 필요하다.
지금부터는 선분과 구 교차 때 테스트했던 방식과 유사하게 진행된다. 양쪽변을 제곱하고 길이의 제곱을 내적으로 바꾼다.
그런 다음 식을 정리하고 변수를 치환한다.
마지막으로 내적을 덧셈 분배 법칙으로 풀고 이차식 형태로 정리한다.
선분과 구체의 교차와 같이 실수해 존재 유무를 결정하기 위해 판별식을 사용한다. 두 개의 값 중에서 최초의 교차점인 작은 의 값이 필요하다. 그리고 선분과 구체의 교차 테스트 처럼 가 범위 [0, 1] 안의 값인지를 검증해야 한다. 아래 코드는 구의 궤적 교차에 대한 코드를 보여준다. 함수는 참조값으로 를 반환하며 호출자는 이 값을 사용해서 교차 시점의 구체의 위치를 결정한다.

