Game Programming in C++ - Day 7

Day 7 벡터와 MoveComonent, InputComponent의 구현

벡터

수학에서 벡터(vector)는 차원당 하나의 요소를 사용해서 n차원에서의 크기와 방향을 나타낸다. 2차원의 벡터는 x, y의 요소를 가지고 있다는 의미다. 게임 프로그래머에게 벡터는 가장 중요한 수학적 도구 중 하나다. 게임상에서 나타나는 수많은 여러 문제들을 해결하는 데 벡터를 사용할 수 있으며, 벡터를 이해하는 것은 3D 게임을 제작할 때 특히 중요하다. 벡터는 위치 개념이 없다. 벡터는 크기와 방향을 갖고 있다. 벡터는 방향을 나타낼 수 있으므로 게임에서는 오브젝트의 방향을 표현하고자 벡터를 종종 사용한다. 오브젝트의 전방 벡터(forward vector)는 오브젝트가 나아가는 직선 방향을 나타내는 벡터다. 개발자는 게임상에서 다양한 벡터 연산을 수행하는데 일반적으로 라이브러리를 사용하기 때문에 어떤 벡터 연산이 어떤 문제를 해결할 수 있는지를 아는 것이 더 좋다. Game Programming in C++에서는 Math.h 헤더 파일에서 벡터 라이브러리를 자체 제작해서 사용한다. 헤더 파일에는 Vector2, Vector3 클래스가 선언돼 있으며, 수많은 연산자와 멤버 함수가 구현돼 있다. x와 y 구성 요소가 public 변수이므로 다음과 같이 코드를 작성할 수 있다.

Vector2 myVector;
myVector.x = 5;
myVector.y = 10;

두 점 사이에서 벡터 얻어내기 : 뺄셈

한 벡터의 각각의 구성 요소와 일치하는 다른 벡터의 구성 요소를 빼면 새로운 벡터를 얻을 수 있다. 예를 들어 2D상에서 x값은 y값과 분리해서 각각 구성 요소 끼리를 뺀다.

$\overrightarrow{c}$ = $\overrightarrow{b} - \overrightarrow{a}$ = <$b_x - a_x, b_y - a_y$>

한 벡터의 머리에서 다른 벡터의 머리까지 그려서 벡터를 완성한다. 뺄셈은 순서에 영향을 받으므로 순서가 중요하다. 우주 게임에서 우주선이 목표물에 레이저를 쏜다고 가정해보자. 점 s는 우주선의 위치이며 점 t는 목표물의 위치이다. 그리고 각각의 위치는 s = (5, 2), t = (3, 5)로 가정한다. 이 점들을 원점이 꼬리이고 머리가 각각의 점들을 가리키는 벡터 $\overrightarrow{s}, \overrightarrow{t}$로 생각해보자. 이전에 설명했듯이 이러한 벡터의 x, y 요소의 값은 점들과 동일하다. 하지만 벡터라면 뺄셈을 사용해서 두 벡터 사이의 새로운 벡터를 만들 수 있다. 레이저는 우주선에서 목표물을 향하므로 이것은 뺄셈을 해당한다.

$\overrightarrow{t}-\overrightarrow{s}$ = <3, 5> - <5, 2> = <-2, 3>

Math.h 라이브러리에서 -연산자는 두 벡터 간 뺄셈을 수행한다.

Vector a, b;
Vector 2 = result = a - b;

벡터 스케일링하기 : 스칼라 곱

스칼라 값은 벳터에 곱하는 것이 가능하다. 벡터의 각각의 요소에 스칼라 값을 곱하면 된다.

$s\cdot$$\overrightarrow{a}$ = <s$\cdot a_x, s\cdot a_y$>

양의 스칼라 값을 벡터에 곱하면 오직 벡터의 크기만을 바꾸는 반면, 음수의 스칼라 값을 곱하면 벡터의 방향을 반전시킨다. Math.h 라이브러리에서 * 연산자는 스칼라 곱을 실행한다.

Vector2 a;
Vector2 result = 5.0f * a;

두 벡터 사이의 결합 : 덧셈

벡터 덧셈에서는 두 벡터의 요소를 각각 더해서 새로운 벡터를 생성한다.

$\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}$ = <$a_x + b_x, a_y + b_y$>

덧셈의 순서는 결과에 영향을 미치지 않는다. 벡더의 덧셈은 두 실수 사이의 덧셈처럼 순서가 크게 상관없기 때문이다. 벡터 덧셈 다양한 방식으로 사용할 수 있다. 예를 들어 플레이어가 p 지점에 있고 플레이어 플레이어의 전방 벡터가 $\overrightarrow{f}$라고 가정하자. 그럼 플레이어 150유닛 앞에 있는 지점은 $\overrightarrow{p} + 150\overrightarrow{f}$가 된다. Math.h 라이브러리에서 +연산자는 두 벡터를 더한다.
거리 결정하기 : 길이
벡터의 크기는 $\vert\vert\overrightarrow{a}\vert\vert$로 쓸수 있다. 벡터의 길이를 구하기 위해서 각 요소의 제곱의 합에 제곱근을 사용하자.

$\vert\vert\overrightarrow{a}\vert\vert$=$\sqrt {a_x^2+a_y^2}$

또한 두 임의의 지점 사이의 거리를 계산하는 데도 이 공식을 사용하는 것이 가능하다. 주어진 점 p, q를 벡터로 생각하고 벡터의 뺄셈을 하고 그 결과로 나온 벡터의 크기는 두 점 사이의 거리와 같다.

distance = $\vert\vert\overrightarrow{p} - \overrightarrow{q}\vert\vert$

이 공식에서 제곱근은 상대적으로 계산 비용이 크다. 반드시 길이를 알아야 한다면 이 제곱근을 피할 방법이 업다. 하지만 어떤 경우에는 제곱근 계산을 하지 않아도 된다. 예를 들어 플레이어가 오브젝트 A에 가까운지 오브젝트 B에 가까운지를 결정해야 한다고 가정하자. 처음에는 오브젝트 A에서 플레이어로의 벡터, $\overrightarrow{p}-\overrightarrow{a}$를 구한다. 유사하게 오브젝트 B에서 플레이어까지의 벡터, $\overrightarrow{p}-\overrightarrow{b}$를 구한다. 어느 오브젝트가 플레이어에 더 가까운지를 알아내기 위해 각 벡터의 길이를 계산해서 비교하는 것은 너무 당연해보인다. 하지만 어느 정도 수학 연산을 간소화하는 것이 가능하다. 허수는 없다고 가정하면 벡터의 길이는 양수이다. 이 경우에 두 벡터의 길이를 비교하는 것은 논리적으로 각 벡터의 길이 제곱값과 비교하는 것과 똑같다.

$\vert\vert\overrightarrow{a}\vert\vert$<$\vert\vert\overrightarrow{b}\vert\vert$ $\equiv$ $\vert\vert\overrightarrow{a}\vert\vert^2$<$\vert\vert\overrightarrow{b}\vert\vert^2$

따라서 단순히 상대적인 비교만을 필요로 하는 경우 길이 대신에 길이의 제곱값을 사용하면 된다.

$\vert\vert\overrightarrow{a}\vert\vert^2$=$\sqrt {a_x^2+a_y^2}$

Math.h 라이브러리에서 Length() 멤버 함수는 a 벡터 길이를 계산한다.

Vector2 a;
float length = a.Length();

마찬가지로 LengthSquared 멤버 함수는 길이의 제곱값을 계산한다.

방항 결정하기 : 단위 벡터와 정규화

단위 벡터(unit vector)는 1의 길이를 가진 벡터다. 단위 벡터의 표기는 $\hat{u}$와 같이 벡터 문자 위에 '모자'를 그려서 나타낸다. 그리고 정규화(normalization)를 거치면 단위 벡터가 아닌 벡터를 단위 벡터로 변환하는 것이 가능하다 벡터를 정규화하려면 벡터의 각 요소를 벡터의 길이로 나누면 된다.

$\hat{u}$ = <$\frac{a_x}{\vert\vert\overrightarrow{a}\vert\vert}$,$\frac{a_y}{\vert\vert\overrightarrow{a}\vert\vert}$>

어떤 경우에는 단위 벡터를 사용하면 계산이 단순해질 수 있다. 하지만 벡터를 정규화하는 것은 벡터의 원래의 크기 정보를 잃는 결과를 초래한다. 그렇기 때문에 정규화할 때는 항상 주의를 기울여야 한다. 그래서 방향만 필요로 할 경우에 벡터를 정규화하는 것이다. 화살표가 가리키는 방향이나 액터의 전방 벡터가 좋은 예에 해당한다. 일반적으로 물체가 어느 방향으로 향하고 있는지를 나타내는 전방 벡터나 어느 방향이 위쪽인지를 나타내는 상향 벡터(up vector)를 정규화한다. 그러나 다른 벡터들의 정규화는 원치 않을 수 있다. 예를 들어 중력 벡터를 정규화해버리면 중력의 크기를 잃어버리게 된다. Math.h 라이브러리는 2개의 다른 Normalize() 함수를 제공한다. 첫 번째는 주어진 벡터를 실제로 정규화 하는 함수다(정규화하지 않은 벡터에 덮어쓴다.)

Vector2 a;
a.Normalize(); // a는 이제 정규화됐다

또한 파라미터로 벡터를 전달받아 정규화한 뒤 그 정규화된 벡터를 반환하는 정적 함수가 있다.

Vector2 a;
Vector2 result = Vector2::Normalize(a);

각도로부터 전방 벡터 변환

이전에 구현한 Actor 클래스는 각도가 라디안 단위인 회전값을 가지고 있었다. 이 값을 사용하면 액터는 자신이 향해야 될 방향으로 회전할 수 있다. 회전은 지금 2D상에서 이루어지므로 각도는 단위 원의 각도와 일치한다.

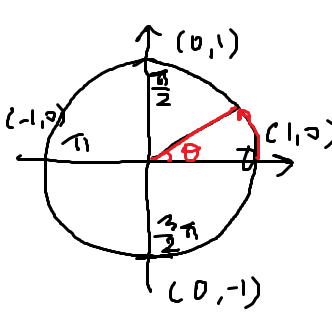
각도를 세타로 표현한 단위 원의 방정식은 다음과 같다

x = cosθ
y = sinθ

이 방정식은 액터의 각도를 전방 벡터로 변환하는 데 바로 사용할 수 있다.

Vector3 Actor::GetForward() const {
	return Vector2(Math::Cos(mRotation), Math::Sin(mRotation)
}

전방 벡터를 각도로 변환 : 아크탄젠트

전방 벡터가 주어졌을 때 이 전방 벡터를 각도로 변환하려 한다. 탄젠트 함수는 각도를 인자로 받고 삼각형의 밑변과 높이의 비율값을 반환한다. 액터의 새로운 전방 벡터로부터 회전 멤버 변수에 해당하는 각도를 구한다고 가정해보자. 전방 벡터 $\overrightarrow{v}$와 x축으로 직각 삼각형을 구성하면 된다. 이 삼각형에서 전방 벡터의 x 요소는 삼각형의 밑변의 길이다. 그리고 전방 벡터의 y 요소는 삼각형의 높이이다. 이 요소들의 비율값을 이용하면 아크탄젠트 함수를 이용해서 각도 세타를 계산하는 것이 가능하다. 프로그래밍에서 선호되는 아크탄젠트 함수는 atan2 함수다. 이 함수는 파라미터로 삼각형의 높이와 밑변의 길이, 2개의 인자를 받는다. 그리고 [-π, π] 범위의 각도를 리턴한다. 양의 각도는 삼각형이 1사분면이나 2사분면의 있고, 음의 각도는 삼각형이 3사분면이나 4사분면에 있다는 걸 뜻한다.

예를 들어 우주선이 운석을 바라본다고 가정하자. 먼저 우주선에서 운석으로 향하는 벡터를 만들고 이 벡터를 정규화해야한다. 다음으로 atan2 함수를 사용해서 새로운 전방 벡터를 각도로 변환한다. 마지막으로 우주선 액터의 회전값을 이 새로운 각도로 설정한다.

SDL 2D 좌표 시스템에서는 +y가 아래로 향하므로 y값을 반전해야 한다.

Vector2 shipToAsteroid = asteroid->GetPosition() - ship->GetPosition();
shipToAsteroid.Normalize();
float angle = Math::Atan2(-shipToAsteroid.y, shipToAsteroid.x);
ship->SetRotation(angle);

아크탄젠트 함수의 사용은 2D 게임에서 매우 잘 작동한다. 하지만 이 아크탄젠트 함수는 모든 물체가 xy평면에 존재하는 2D 게임과 같은 경우에만 동작한다. 3D 게임에서는 내적을 통한 접근법을 사용하는 것이 좋다.

두 벡터 사이의 각도 구하기 : 내적

두 벡터 사이의 내적(dot product) 결과는 단일 스칼라 값이다. 게임에서 내적을 사용하는 가장 일반적인 경우는 두 벡터 사이의 각도를 찾는 것이다. 다음 방정식은 벡터 $\overrightarrow{a}$와 $\overrightarrow{b}$의 내적을 계산한다.

$\overrightarrow{a}\cdot\overrightarrow{b}$ = $a_x\cdot b_x + a_y\cdot b_y$

또한 내적은 각의 코사인과 관계가 있다. 그래서 두 벡터 사이의 각도는 다음과 같이 표현할 수 있다.

$\overrightarrow{a}\cdot\overrightarrow{b}$ = $\vert\vert\overrightarrow{a}\vert\vert$$\vert\vert\overrightarrow{b}\vert\vert$cosθ

그래서 내적을 이용하면 세타를 구할 수 있다.

θ = arccos($\overrightarrow{a}\cdot\overrightarrow{b}\over \vert\vert\overrightarrow{a}\vert\vert\vert\vert\overrightarrow{b}\vert\vert$)

두 벡터 $\overrightarrow{a}$, $\overrightarrow{b}$가 단위 벡터라면 각 벡터의 길이가 1이므로 분모를 생략할 수 있다.

θ = arccos($\hat{a}\cdot\hat{b}$)

단위 벡터를 사용했으므로 식이 단순해졌는데, 방향만이 중요하다면 미리 벡터를 정규화해두는 것이 좋다.두 벡터 사이의 각도를 계산할 시 내적에서 발생할 수 있는 몇 가지 특별한 경우를 기억해두면 좋다. 두 단위 벡터 사이의 내적이 0이면 두 벡터가 수직한다는 것을 뜻한다. 또한 내적값이 1이라면 두 벡터는 평행해서 같은 방향으로 향하고 있다는 걸 뜻한다. 마지막으로 -1은 두 벡터가 서로 평행하지만 반대 방향으로 향하고 있다는 걸 의미한다. 각도를 계산하기 위해 내적을 사용할 경우 한 가지 결점은 아크코사인이 [0, π]범위에서 각도를 반환한다는 것이다. 이 떄문에 아크코사인은 두 벡터 사이의 최소 회전값을 주지만 이 회전값이 시계 방향인지 아니면 반시계 방향인지 알 수 없다. Math.h 라이브러리에서는 vector2와 Vector3에 대한 Dot 정적 함수를 정의했다.

float dotResult = Vector2::Dot(origForward, newForward);
float angle = Math::Acos(dotResult);

법선 벡터 계산하기 : 외적

법선 벡터(normal vector)는 표면에 수직한 벡터다. 표면의 법선 벡터를 계산하면 3D 게임에서 매우 도움이 된다. 평행하지 않은 2개의 3D 벡터가 주어지면 두 벡터를 포함하는 평면은 반드시 존재한다.외적은 그 평면의 수직한 벡터를 구한다. 외적은 2D 벡터에서는 동작하지 않는다. 그러나 2D 벡터를 3D 벡터로 변환하면 사용할 수 있다. 2D 벡터를 3D 벡터로 변환하려면 z 요소값 0을 2D 벡터에 추가하면 된다. x 기호는 두 벡터 사이의 내적을 뜻한다.

$\overrightarrow{c}$ = $\overrightarrow{a}\times\overrightarrow{b}$

외적의 수치 계산은 다음과 같다.

$\overrightarrow{c}$ = $\overrightarrow{a}\times\overrightarrow{b}$ = <$a_yb_z-a_zb_y$, $a_zb_x - a_xb_z$, $a_xb_y - a_yb_x$>

내적처럼 외적에서도 특별히 고려해야하는 경우가 있다. 외적이 벡터 (0, 0, 0)을 반환하면 $\overrightarrow{a}$와 $\overrightarrow{b}$가 평행하다는 것을 뜻한다. 두 평행한 벡터는 평면을 형성할 수 없다. 그래서 외적은 반환할 법선 벡터를 가지지 못한다. Math.h 라이브러리는 정적 함수 Cross를 제공한다.

Vector3 c = Vector3::Cross(a, b);

기본 이동

이동은 게임의 일반적인 특징이므로 컴포넌트로 이동 행위를 캡슐화하는 것이 좋다. 그래서 이번 챕터에서는 액터가 게임 세계 주변을 돌아다닐수 있도록 MoveComponent 클래스를 제작하는 방법을 설명하고 키보드 입력을 직접 가져올 수 있는 MoveComponent의 서브클래스인 InputComponent를 만드는 방법을 살펴본다. 기본 수준에서 MoveComponent는 액터가 특정 속도로 앞을 향해 나아갈 수 있도록 해야 한다. 특정 속도로 나아가는 것을 지원하려면 먼저 액터의 전박 벡터를 계산하는 함수가 필요하다. 액터의 전방 벡터를 구했다면, 전진하는 액터의 위치를 다음과 같은 의사 코드로 표현하는 것이 가능하다.

position += GetForward() * forwardSpeed * deltaTime;

액터의 회전(각도)을 갱신할때는 초당 회전을 나타내는 각속도와 델타 시간만이 필요하다.

rotation += angularSpeed * deltaTime;

이렇게 위치값과 회전값 갱신을 구현하면 액터는 상대적인 속도값에 의존해서 전진과 회전을 할 수 있다.

MoveComponent.h

MoveComponent는 전진과 회전 이동을 위해 별도의 속도값을 가지고 있으며 이 속도에 대한 getter/setter 함수를 가지고 있다. 또한 MoveComponent 클래스는 Update 함수를 재정의해서 액터를 움직이는 코드를 구현한다. MoveComponent의 생성자에서는 기본 갱신 순서값을 10으로 지정했다. 갱신 순서는 액터가 어떤 컴포넌트를 먼저 갱신할지에 관한 순서를 결정하므로 다른 컴포넌트 보다 MoveComponent가 앞서 갱신된다.

Component 클래스는 mOwner 멤버 변수를 통해 자신의 소유가에 접근할 수 있다. 아 mOwner 포인터를 이용하면 소유자 액터의 위치값과 회전값, 그리고 전방 벡터 값에 접근할 수 있다. Math::NearZero 함수는 파라미터의 절댓값이 0에 가까운지 결정하기 위해 작은 값인 엡실론(0.001)과 비교한다. 이 아주 작은 값인 엡실론보다 작으면 속도는 0에 가깝다고 판단하고 액터의 회전이나 위치를 갱신하지 않는다. 이번 챕터의 게임 프로젝트는 고전 애스터로이드 게임 버전이므로 또한 화면 래핑을 위한 코드도 필요하다. 그러나 일반적으로 MoveComponent에서 필요한 내용은 아니다. 이제 MoveComponent가 부착된 Actor의 서브클래스인 Asteroid를 선언한다.

Asteroid.cpp

Asteroid의 생성자에서는 운석에 이미지를 씌우기 위해 SpriteComponent도 가져온다. 그리고 랜덤 함수를 이용해 함수의 위치와 방향을 랜덤으로 설정한다. Random.h 라이브러리는 단순히 벡터나 특정 범위에 있는 실수값을 얻기 위해 C++에 내장된 무작위 수 생성 함수를 감싼 것에 불과하다. 그리고 Asteroid 클래스를 사용해서 Game::LoadData에서 운석을 생성한다.

InputComponent 클래스 제작

기본 MoveComponent는 플레이어가 제어하지 않는 운석과 같은 물체에 관해서는 문제될 것이 없다. 그러나 플레이어가 키보드로 우주선을 제어하기를 원한다면 딜레마에 빠질 것이다. 그래서 입력을 액터나 컴포넌트로 연결해 게임 객체 모델에 입력을 통합하는 것이 좋다. 즉 상황에 따라 액터나 컴포넌트의 서브클래스가 입력을 재정의할 수 있는 함수가 필요하다. 이를 지원하기 위해 먼저 Component에 빈 가상 함수 ProcessInput을 추가한다.

virtual void ProcessInput(const uint8_t keyState) {}

그런 다음 액터에서 ProcessInput, ActorInput(가상 함수) 두 함수를 선언한다. 커스텀 입력이 필요한 액터의 서브클래스는 ProcessInput이 아닌 ActorInput을 재정의한다.

Actor::ProcessInput 함수는 먼저 액터의 상태가 활성화돼 있는지 확인하고 활성화되어 있다면 모든 컴포넌트의 ProcessInput을 호출한다. 그리고 다음 액터가 재정의된 행위를 하도록 ActorInput을 호출한다.

마지막으로 Game::ProcessInput에서는 모든 액터를 반복하면서 각 액터의 ProcessInput을 호출한다. ProcessInput 내부에서 액터가 또다른 액터를 만들려고 하거나 액터가 컴포넌트를 다루는 루프 앞에서는 mUpdatingActors bool 값이 true로 설정되어야 한다. 그리고 새로운 액터를 추가할 떄는 mActors 대신에 mPendingActors에 추가해야한다.

InputComponent.h

이제 InputComponent라는 MoveComponent의 서브클래스를 선언한다. InputComponent의 주된 임무는 소유자 액터의 이동과 회전을 제어하는 특정 키를 설정하는 것이다. 또한 재정의된 ProcessInput이 직접 MoveComponent의 전방 속도와 각 속도를 설정하므로 비정상적인 속도값이 설정되지 않도록 최대 속도에 제한을 둔다.

InputComponent::ProcessInput에서는 전방 속도를 0으로 하고 눌러진 키에 따라 올바른 전방 속도를 결장한다. 그리고 이 속도를 SetForwardSpeed로 넘긴다. 각 속도를 설장하는 코드도 전방 속도를 설정하는 코드와 비슷하다.

Ship.cpp