Day 8 충돌 감지
뉴턴 물리
일부 게임에서는 실제 세계와 유사한 이동에 관해서 물리적으로 정확한 접근이 필요하다. 게임에서는 일반적으로 뉴턴 물리(고전 물리)를 사용한다. 물체가 빛의 속도에 근접할 정도로는 이동하지 않고 양자 입자보다 크다면 뉴턴 물리가 제대로 성립하기 때문이다. 게임은 일반적으로 양자 물리가 적용되는 예외적 상황의 물체를 다루지 않기 때문에 뉴턴 물리가 잘 적용된다. Game Progamming in C++에서는 오직 회전력이 없는 운동 또는 선형 역학(linear mechanics)처럼 가장 기본적은 운동만을 고려한다. 선형 역학의 2가지 핵심은 힘과 질량이다. 힘은 물체가 움직이는데 영향을 미친다. 힘(Force)는 크기와 방향을 갖고 있으므로 힘을 벡터로 표현하는 것이 자연스럽다. 질량(Mass)는 물체에 내포된 물질의 양을 나타내는 스칼라다. 물체의 질량이 크면 클수록 물체의 운동을 변경하는 것은 어려워진다. 물체의 힘이 충분히 주어지면 물체는 움직이기 시작한다. 뉴턴의 제2운동법칙은 이러한 개념을 내포한다.
힘은 질량x가속도와 같으므로 가속도는 힘을 질량으로 나눈 값이다. 게임에서 임의의 물체는 질량을 갖고 있으며, 그 물체에 힘을 가하는 것은 게임에서의 일상적인 접근법이다. 이러한 접근법으로 개발자는 물체의 가속도를 계산한다. 물리학에서 선형 역학은 위치와 속도와 가속도를 시간에 따른 함수로 표현하며 이러한 함수는 기호로 표현된다. 그리고 미적분을 사용해서 속도함수를 위치 함수의 미분으로 표현하고, 가속도 함수를 속도 함수의 미분으로 표현한다. 그러나 이러한 공식들은 기호로된 방정식이라는 점, 미분이 사용되므로 게임에서 사용되기 어렵다. 게임에서는 물체에 힘을 가하는 동안 시간의 변화에 따른 가속도를 구하는 것이 중요하다. 물체의 가속도를 얻으면 물체의 속보 변화를 계산할 수 있다. 마지막으로 속도가 주어지면 물체의 위치 변화를 계산할 수 있다. 게임에서는 델타 시간, 즉 이산 시간 값을 사용해서 사용하므로 기호 방정식이 필요치는 않고 적분을 사용해야한다. 하지만 기호로 표현되는 적분이 아닌 수치 적분을 사용해야한다. 수치 적분은 기호 적분을 고정된 시간 간격으로 근사화한다. 수치 적분을 통해서 게임은 가속도를 기반으로 속도를 갱신한 다음, 속도를 기반으로 위치를 갱신한다. 그러나 물체의 가속도를 계산하기 위해 게임은 물체에 적용된 힘뿐만 아니라 물체의 질량도 알 필요가 있다. 또한 고려해야하는 다양한 유형의 힘이 존재한다. 중력 같은 일부 힘은 일적하며 프레임마다 적용해야한다. 대신에 다른 힘들은 단일 프레임에만 적용되는 충격(impulse)이나 힘일 수 있다. 예를 들어 캐릭터가 점프할 때는 반발력으로 인해 플레이어는 땅에서 벗어날 수 있따. 그러나 캐릭터는 최종적으로 땅으로 되돌아올 것이다. 왜냐하면 일정한 힘의 크기를 지닌 중력때문이다. 다양한 힘이 물체에 동시에 작용하며 모든 힘은 벡터이므로 모든 힘을 더하면 해당 프레임마다 물체에 적용될 전체 힘을 구할 수 있다. 힘들의 총합을 질량으로 나누면 가속도를 얻는다.
acceleration = sumOfForces / mass;속도와 위치를 계산하기 위해 수치 적분인 오일러 적분을 사용한다.
// 오일러 적분
// 속도 갱신
velocity += acceleration * deltaTime;
// 위치 갱신
position += velocity * deltaTime;이 계산에서는 힘, 가속도, 속도, 위치가 모두 벡터로 표시된다. 이 계산은 델타 시간에 의존하므로 물리를 시뮬레이션 하는 컴포넌트의 Update 함수에 넣는다. 물리 시뮬레이션에 의존하는 게임의 경우 가변 프레임 시간(또는 시간 단계(time step)은 문제의 소지가 된다. 수치 적분의 정확도가 시간 단계의 크기에 의존하기 때문이다. 시간 단계가 작을수록 근사값은 더욱더 정확하다. 또한, 프레임 레이트가 프레임마다 다를 경우 수치 적분의 정확도가 달라진다. 정확도의 변화는 게임 동작에 매우 큰 영향을 미친다. 예를 들어 게임에서 캐릭터가 점프를 한다고 했을때 점프할 수 있는 거리는 프레임 레이트에 따라 달라져서 프레임 레이트가 낮을수록 더 멀리 점프하게 된다. 이는 프레임 레이트가 낮을수록 수치 적분의 오차가 커지기 때문이며, 왜곡된 점프 곡선을 초래한다.
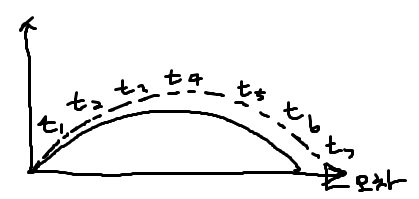
이런 이유로 물체의 위치를 계산하는 물리를 사용하는 게임에서는 가변 프레임 레이트를 사용하지 말아야한다. 대신에 프레임을 제한하면 프레임 레이트가 목표 프레임 레이트를 초과하지 않으면 잘 동작한다. 더 복잡하게는 큰 시간 단계를 고정된 크기의 물리 시간 단계로 나누는 것을 고려해볼 수 있다.
기본 충돌 감지
충돌 감지(collosion detection)는 게임 세계에서 두 물체가 서로 접촉하는지 결정하는 방법이다. 충돌 감지에서 핵심 개념은 문제의 단순화다. 예를 들어 운석 이미지는 원이긴 하지만 정확하게 원은 아니다. 운석의 실제 윤곽에 대해 충돌을 테스트하는 것이 보다 정확하겠지만, 충돌 감지란 목적에서는 운석을 원으로 생각하는 것이 보다 효율적이다. 비슷하게 레이저를 원으로 단순화하면 이 두 원이 충돌하는지만 결정하면 된다.
두 원의 교차
두 원은 두 원 중심점 사이의 거리가 두 원 반지름 합보다 같거나 작은 경우에만 서로 교차한다.

위 그림에서 첫 번째는 두 원이 교차하지 않을 정도로 멀리 떨어져 있다. 이 경우에 원들 중심점 사이의 거리는 두 반지름의 합보다 크다. 그러나 두 번째는 원이 교차하는데 이 경우 두 중심 사이의 거리는 두 원의 반지름의 합보다 작다. 이 교차 테스트를 수행하려면 두 원 중심점 사이의 벡터를 만들고, 이 벡터의 크기를 계산해야 한다. 그런 후 각 반지름의 합과 이 벡터의 크기를 비교한다.
원이 교차할 경우 필요한 것은 거리와 반지름의 합 간의 비교이다. 거리와 두 원의 반지름의 합이 음수일 수는 없기에 방정식의 양쪽 항을 제곱해도 항등성은 유지된다.
이러한 접근법은 구에서도 같은 원리가 적용된다.
CircleComponent 서브클래스 제작
액터의 충돌 감지를 지원하기 위해 CircleComponent를 만들고, 두 원 컴포넌트 사이의 교차를 테스트할 방법을 만들자. 그런 다음 CircleComponent를 충돌이 필요한 액터에 추가한다.
CircleComponent.h

먼저 Component의 서브클래스로서 CircleComponent를 선언한다. CircleComponent의 유일한 멤버 변수는 반지름이다. 원의 중심은 소유자 액터의 위치이다. 그리고 두 개의 원 컴포넌트를 파라미터로 받고 두 원이 서로 교차하면 true를 반환하는 전역 함수 InterSect 함수를 선언한다.

Intersect 함수에서는 두 원의 중심 사이의 거리의 제곱값을 계산하고 두 원의 반지름의 합의 제곱값을 비교해서 두 원의 반지름의 합의 제곱값이 더 작다면 교차하는 것으로 판단하고 true를 반환한다. 이제 Asteroid에 CircleComponent를 추가한다.
mCircle = new CircleComponent(this);
mCircle->SetRadius(40.0f);그리고 우주선이 발사할 Laser 서브클래스를 하나 더 만든다.

Laser::UpdateActor에서는 운석과 교차 여부를 테스트한다. 운석과 레이저가 교차한다면 충돌했다고 판단하고 레이저와 운석의 상태를 EDead로 바꿔서 사라지게 만든다. 이번 게임의 경우에는 운석과 원이 비슷하기 때문에 원으로 충돌하는 것이 잘 작동하지만 원이 모든 유형의 물체에 대해서는 잘 작동하지 않으며, 특히 3D에서는 잘 동작하지 않는다.
그리고 우주선을 담당하는 Ship 클래스에 스페이스를 누르면 레이저가 발사되도록 하기 위해 새롭게 입력 감지를 추가해 주는데 레이저 발사는 우주선만의 것이므로 ActorInput에 추가해준다.

레이저가 계속 발사되는 것을 방지하고자 쿨타임 0.5초를 정해주고 Laser::UpdateActor에서 쿨타임을 델타 시간으로 감소시켜준다.
void Ship::UpdateActor(float deltaTime) {
mLaserCooldown -= deltaTime;
}그래서 유저가 스페이스를 누르고 mLaserCooldown이 0보다 작다면 레이저가 발사되도록 한다.

