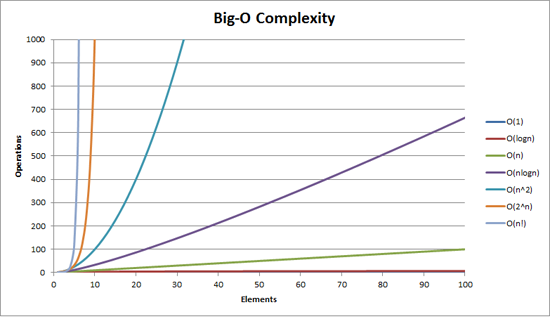
시간 복잡도
시간 복잡도는 주어진 문제를 해결하기 위해 수행한 연산 횟수를 의미하며, 일반적으로 1억 번의 연산을 1초의 시간으로 간주하여 예측한다.
시간 복잡도 유형
int findNumber = (int)(Math.random() * 100);
for (int i = 0; i < 100; i++) {
if (i == findNumber) {
System.out.println(i);
break;
}
}위 코드 예제를 통해 시간 복잡도를 살펴보면 다음과 같이 표기할 수 있다.
- 빅-오메가(Ω(n) = 1번) : 최선일 때(best case)의 연산 횟수
- 빅-세타(Θ(n) = 2/N번 = 50번) : 보통일 때(average case)의 연산 횟수
- 빅-오(O(n) = N번 = 100번) : 최악일 때(worst case)의 연산 횟수
항상 최악의 경우를 염두해야하기 때문에 빅-오 표기법을 사용해야 한다.
시간 복잡도 도출 기준
- 상수는 시간 복잡도 계산에서 제외한다.
- 가장 많이 중첩된 반복문의 수행 횟수가 시간 복잡도의 기준이 된다.
int N = 100_000;
int cnt = 0;
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수 : " + cnt++);
}int N = 100_000;
int cnt = 0;
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수 : " + cnt++);
}
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수 : " + cnt++);
}
for (int i = 0; i < N; i++) {
System.out.println("연산 횟수 : " + cnt++);
}위의 두 예제의 연산 횟수는 N번과 3N번으로 3배의 차이가 난다. 그러나 상수는 일반적으로 시간 복잡도 계산에서 제외되므로 두 코드 모두 O(N)의 시간 복잡도를 갖는다.
int N = 100_000;
int cnt = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
System.out.println("연산 횟수 : " + cnt++);
}
}그러나 위의 코드에서는 중첩된 반복문을 기준으로 시간 복잡도가 도출되므로 N²이 된다.
그렇기에 효율적인 알고리즘을 짜기 위해서는 시간 복잡도를 고려하여 알맞은 알고리즘을 선택하고, 비효율 적인 로직을 찾아 효율적으로 최적화하는 작업이 필요하다.
