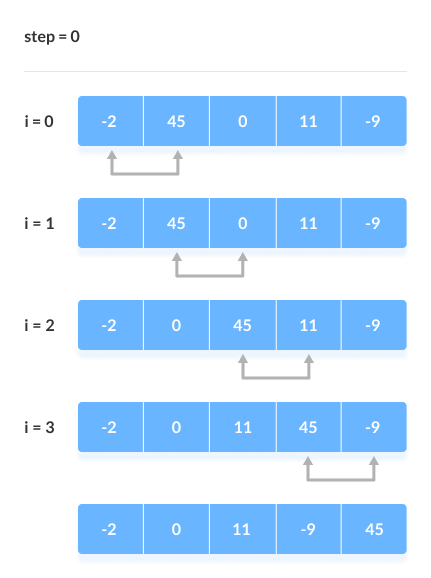
버블 정렬
버블 정렬은 loop를 돌며 데이터의 인접 요소끼리 비교하고, swap 연산을 수행하면 정렬하는 방식이다. 간단하게 구현할 수 있지만, 시간 복잡도가 O(n²)으로 다른 정렬 알고리즘보다 속도가 느린 편이다.
버블 정렬 과정
- 비교 연산이 필요한 루프 범위 설정
- 인접한 데이터 값 비교
- swap 조건에 부합하면 swap 연산 수행
- 루프 범위가 끝날 때까지 2~3번 반복
- 정렬된 정렬 영역을 설정하여 다음 루프 실행시 이 영역 제외
- 비교 대상이 존재하지 않을 때 까지 위의 과정 반복
만약 특정한 루프의 전체 영역에서 swap이 한 번도 발생하지 않았다면 그 영역 뒤에 있는 데이터가 모두 정렬되었다는 뜻이 되며, 프로세스를 종료해도 된다.
버블 정렬 구현
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - 1 - i; j++) {
if (a[j] > a[j + 1]) {
int num = a[j];
a[j] = a[j + 1];
a[j + 1] = num;
}
}
}
for (int i = 0; i < n; i++) {
System.out.println(a[i]);
}
}
}선택 정렬
선택 정렬은 대상 데이터에서 최대나 최소 데이터를 데이터가 나열된 순으로 찾아가며 선택하는 방법이다. 구현 방법이 복잡하고, 시간 복잡도도 O(n²)으로 비효율적이다.
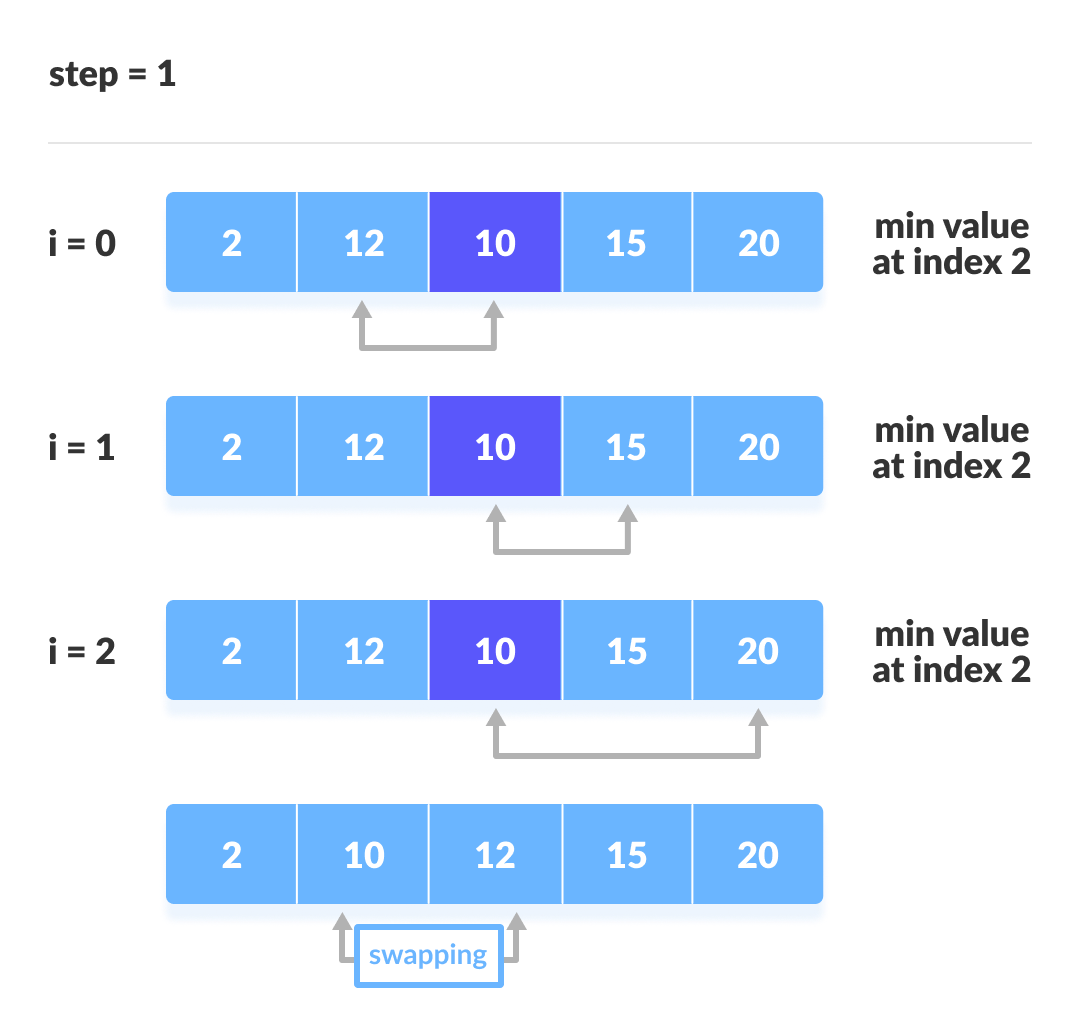
선택 정렬 구현
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String str = sc.next();
int[] a = new int[str.length()];
for (int i = 0; i < str.length(); i++) {
a[i] = Integer.parseInt(str.substring(i, i+1));
}
for (int i = 0; i < a.length; i++) {
int max = i;
for (int j = i + 1; j < a.length; j++) {
if (a[max] < a[j]) {
max = j;
}
}
if (a[i] < a[max]) {
int num = a[i];
a[i] = a[max];
a[max] = num;
}
}
for (int i = 0; i < a.length; i++) {
System.out.print(a[i]);
}
}
}삽입 정렬
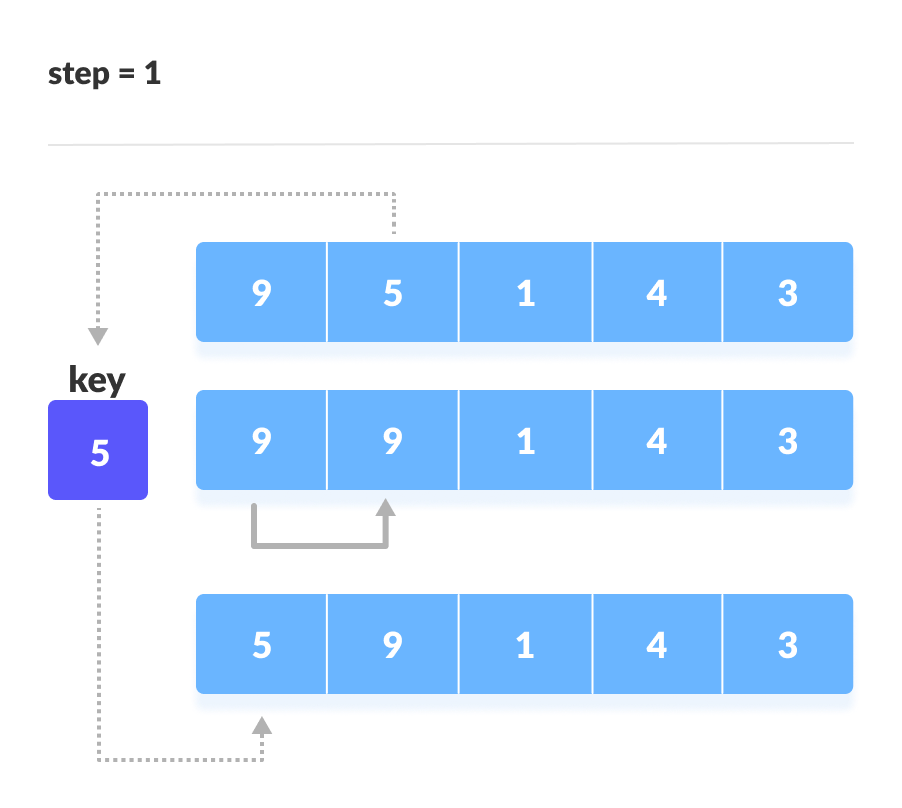
이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식으로 O(n²)의 시간 복잡도로 느린 편이지만 구현이 쉽다. 선택 데이터를 현재 정렬된 데이터 범위 내 적절한 위치에 삽입하는 것이 핵심이다.
삽입 정렬 과정
- 현재 index에 있는 데이터 값 선택
- 선택한 데이터가 정렬된 데이터 범위에 삽입될 위치 탐색
- 삽입 위치부터 index까지 shif연산 수행
- 삽입 위치에 현재 선택한 데이터를 삽입한 후 index++
- 선택할 데이터가 없을 때 까지 반복(전체 데이터의 크기만큼 index가 커질 때 까지)
적절한 삽입 위치를 탐색할 때 이진 탐색과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다.
퀵 정렬
기준값을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복하여 정렬한다. 기준값(pivot) 선정 기준이 시간 복잡도에 많은 영향을 미치며, 평균 시간 복잡도는 O(nlogn)이며, 최악의 경우 O(n²)이 된다.
퀵 정렬 과정
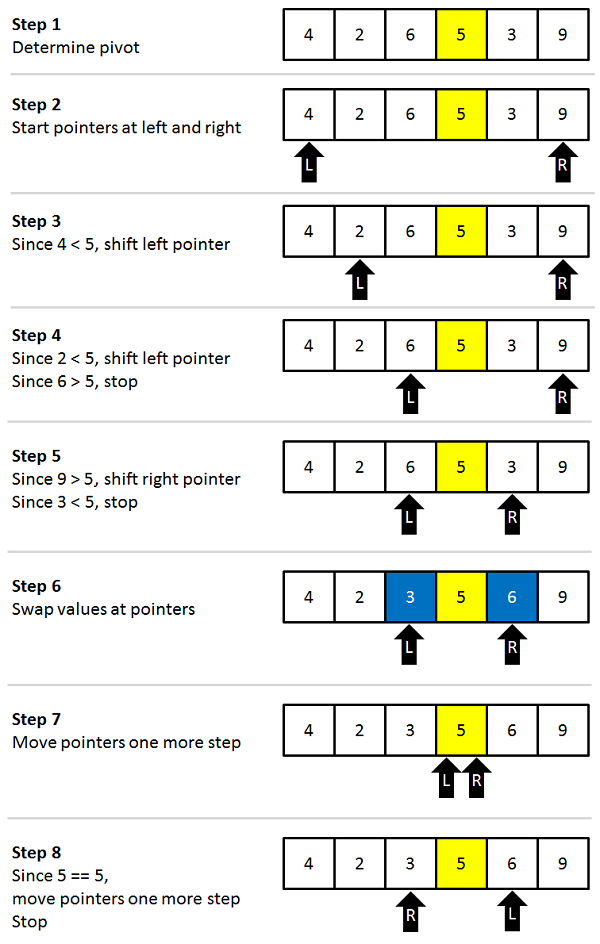
- 데이터를 분할하는 pivot 설정
- pivot을 기준으로 다음 과정을 거쳐 데이터를 2개의 집합으로 분리
- L이 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 L을 오른쪽으로 한칸 이동
- R이 가리키는 데이터가 pivot이 가리키는 데이터보다 크면 R을 왼쪽으로 한칸 이동
- L이 가리키는 데이터가 pivot이 가리키는 데이터보다 크고, R이 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 L, R이 가리키는 데이터를 swap하고, L은 오른쪽, R은 왼쪽으로 한칸씩 이동
- L과 R이 만날 때 까지 위의 과정을 반복
- L과 R이 만나면 만난 지점에서 가리키는 데이터와 pivot이 가리키는 데이터를 비교하여 pivot이 가리키는 데이터가 크면 만난 지점의 오른쪽에, 작으면 만난 지점의 왼쪽에 pivot이 가리키는 데이터를 삽입
- 분리 집합에서 각각 다시 pivot을 선정
- 분리 집합이 한개 이하가 될 때까지 위의 모든 과정을 반복
병합 정렬
분할 정복 방식을 사용해 데이터를 분할하고, 분할한 집합을 정렬하며 합치는 정렬방법이며, 시간 복잡도는 O(nlogn)이다.
두 그룹을 병합하는 과정
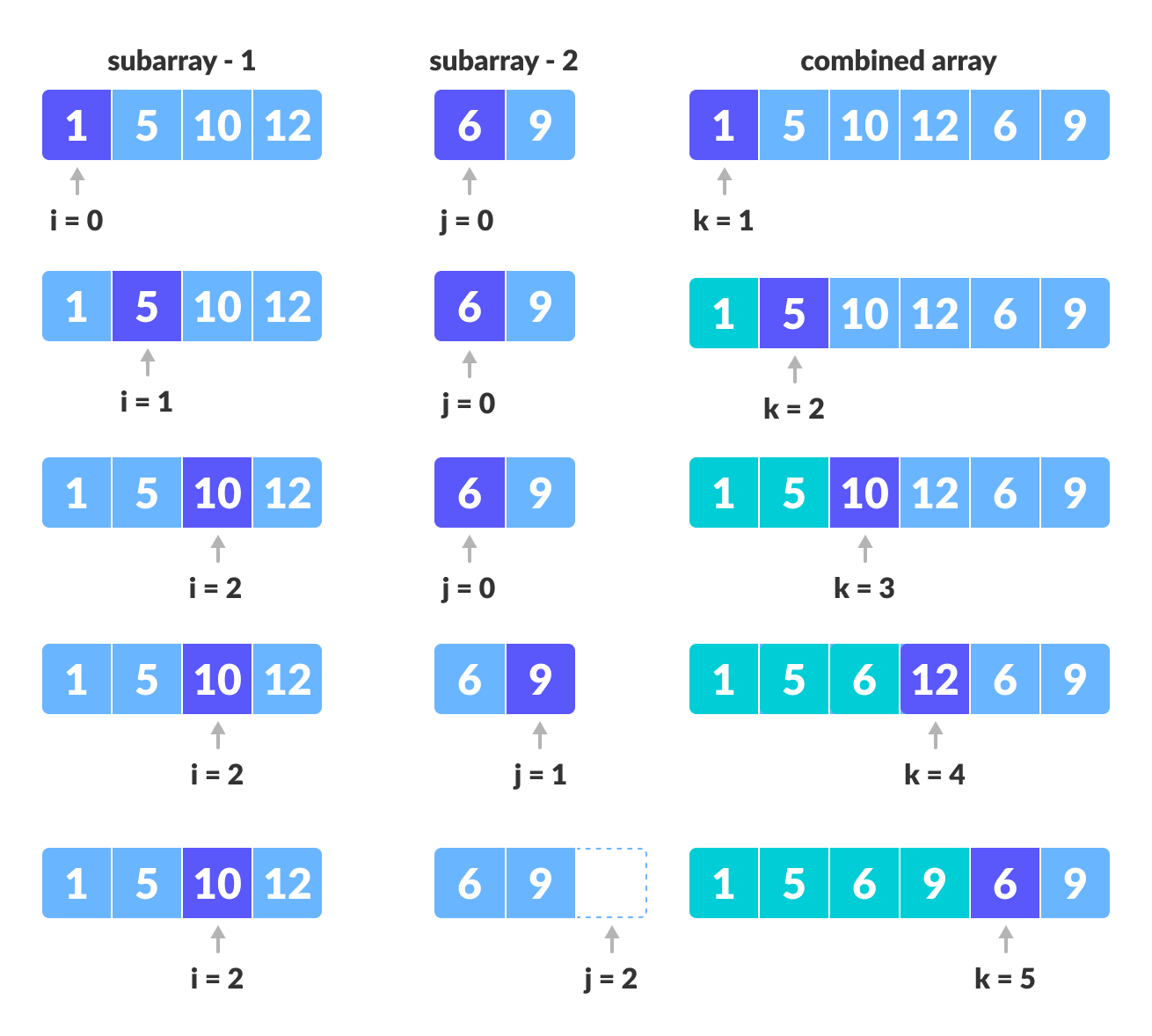
투 포인터 개념을 사용하여 두 그룹을 병합한다. 왼쪽 포인터(i)와 오른쪽 포인터(j)의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 이동시킨다.
병합 정렬 구현
public class MergeSort {
public static void main(String[] args) {
int[] arr = { 9, 7, 3, 1, 6, 2, 8, 4, 5 };
mergeSort(arr, 0, arr.length - 1);
for (int i : arr) {
System.out.print(i + " ");
}
}
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2; // 중간 지점 계산
mergeSort(arr, left, mid); // 왼쪽 반 정렬
mergeSort(arr, mid + 1, right);// 오른쪽 반 정렬
merge(arr, left, mid, right); // 정렬된 반들을 병합
}
}
public static void merge(int[] arr, int left, int mid, int right) {
int[] tempArr = new int[right - left + 1]; // 병합을 위한 임시 배열 생성
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) { // 병합
if (arr[i] <= arr[j]) {
tempArr[k++] = arr[i++];
} else {
tempArr[k++] = arr[j++];
}
}
// 왼쪽 반 나머지 항목들 복사
while (i <= mid) {
tempArr[k++] = arr[i++];
}
// 오른쪽 반 나머지 항목들 복사
while (j <= right) {
tempArr[k++] = arr[j++];
}
// 임시 배열을 복사하여 정렬된 배열로 업데이트
for (i = left, k = 0; i <= right; i++, k++) {
arr[i] = tempArr[k];
}
}
}
기수 정렬
값을 비교하지 않고 비교할 자릿수를 정한 후 해당 자릿수만 비교하는 정렬 방식으로 시간 복잡도는 O(kn)이다. k는 데이터의 자릿수를 의미한다.
기수 정렬은 10개의 큐를 이용(0 ~ 9의 수를 담기 위해)하며, 각 큐는 값의 자릴수를 대표한다.

