DFS(깊이 우선 탐색)
깊이 우선 탐색은 그래프 완전 탐색 기법 중 하나로, 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘이다.
특징으로는 재귀 함수로 구현되며, 스택 자료구조를 이용한다. 노드 개수를 V, 에지 개수를 E라고 할 경우 시간 복잡도는 O(V + E)이다.
깊이 우선탐색은 재귀 함수를 이용하므로 스택 오버플로우(stack overflow)에 유의해야 한다.
핵심 이론
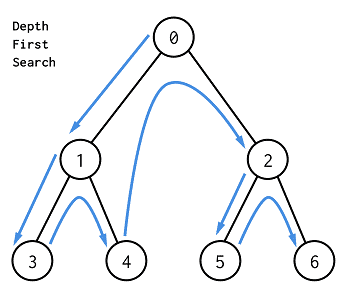
1. DFS 시작 노드를 정한 후 사용할 자료구조 초기화
DFS를 위한 초기 작업은 인접 리스트로 그래프를 표현하고, 방문했던 노드를 체크하기 위한 방문 배열을 초기화한 후 시작 노드 스택에 한다.
2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입
스택에 들어있던 노드를 꺼낸 후 탐색 순서에 기입하고, 인접 리스트의 인접 노드를 스택에 삽입하며 방문 배열을 체크한다.
3. 스택 자료구조에 값이 없을 때 까지 반복
위의 과정을 스택 자료구조에 값이 없을 때까지 반복한다. 이 때 이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심이다.
DFS 구현
import java.io.*;
import java.util.*;
class Main {
static boolean[] VISITED;
static ArrayList<Integer>[] A;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
VISITED = new boolean[n + 1];
A = new ArrayList[n + 1];
for (int i = 1; i < n + 1; i++) {
A[i] = new ArrayList<>();
}
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken());
int e = Integer.parseInt(st.nextToken());
A[s].add(e);
A[e].add(s);
}
int count = 0;
for (int i = 1; i < n + 1; i++) {
if (!VISITED[i]) {
count++;
DFS(i);
}
}
System.out.println(count);
}
public static void DFS(int v) {
if (VISITED[v]) {
return;
}
VISITED[v] = true;
for (int i : A[v]) {
if (!VISITED[i]) {
DFS(i);
}
}
}
}BFS(너비 우선 탐색)
그래프 완전 탐색 기법 중 하나로, 시작 노드에서 출발해 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다. 노드 개수를 V, 에지 개수를 E라고 할 경우 시간 복잡도는 O(V + E)이다.
선입선출 방식으로 탐색하므로 큐를 이용해 구현하며, 탐색 시작 노드와 가까운 노드를 우선 탐색하므로 목표 노드에 도착하는 경로가 여러 개일 때 최단 경로를 보장한다.
핵심 이론
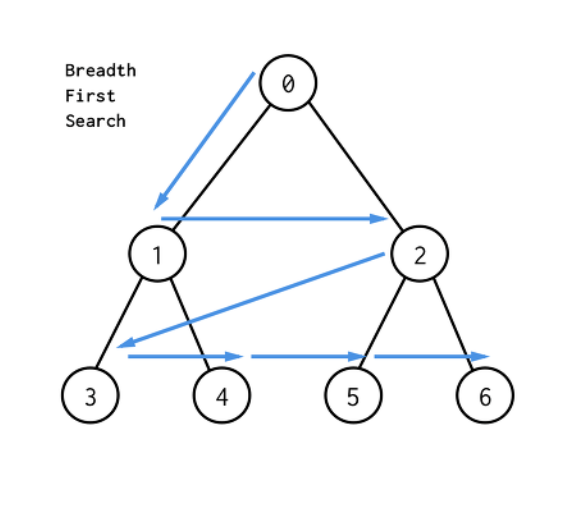
1. BFS 시작 노드를 정한 후 사용할 자료구조 초기화
인접 리스트로 그래프를 표현하고, 방문했던 노드를 체크하기 위한 방문 배열을 초기화한 후 시작 노드 큐에 한다.
2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입
큐에 들어있던 노드를 꺼낸 후 탐색 순서에 기입하고, 인접 리스트의 인접 노드를 큐에 삽입하며 방문 배열을 체크한다.
큐 자료구조에 값이 없을 때 까지 반복
위의 과정을 큐 자료구조에 값이 없을 때까지 반복한다. 이 때 이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심이다.
BFS 구현
import java.util.*;
import java.io.*;
class Main {
static int[] DX = {0, 1, 0, -1};
static int[] DY = {1, 0, -1, 0};
static boolean[][] VISITED;
static int[][] A;
static int N, M;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
A = new int[N][M];
VISITED = new boolean[N][M];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
String line = st.nextToken();
for (int j = 0; j < M; j++) {
A[i][j] = Integer.parseInt(line.substring(j, j + 1));
}
}
BFS(0, 0);
System.out.println(A[N - 1][M - 1]);
}
private static void BFS(int i, int j) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[] {i, j});
VISITED[i][j] = true;
while (!queue.isEmpty()) {
int now[] = queue.poll();
for (int k = 0; k < 4; k++) {
int x = now[0] + DX[k];
int y = now[1] + DY[k];
if (x >= 0 && y >= 0 && x < N && y < M) {
if (A[x][y] != 0 && !VISITED[x][y]) {
VISITED[x][y] = true;
A[x][y] = A[now[0]][now[1]] + 1;
queue.add(new int[] {x, y});
}
}
}
}
}
}이진 탐색
이진 탐색(binary search)은 데이터가 정렬되어 있는 상태에서 원하는 값을 찾아내는 알고리즘으로, 대상 데이터의 중앙값과 찾고자 하는 값을 비교해 데이터의 크기를 절반씩 줄이면서 대상을 찾는 알고리즘이다.
핵심 이론

- 현재 데이터셋의 중앙값을 선택
- 중앙값 > 타깃 데이터일 경우 중앙값 기준으로 왼쪽 데이터셋 선택
- 중앙값 < 타깃 데이터일 경우 중앙값 기준으로 오른쪽 데이터셋 선택
- 1 ~ 3을 반복하며 중앙값 == 타깃 데이터일 때 탐색 종료
이진 탐색 구현
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt();
int[] A = new int[N];
for (int i = 0; i < N; i++) {
A[i] = sc.nextInt();
}
Arrays.sort(A);
int M = sc.nextInt();
for (int i = 0; i < M; i++) {
boolean find = false;
int target = sc.nextInt();
int start = 0;
int end = A.length - 1;
while (start <= end) {
int mid = (start + end) / 2;
int midValue = A[mid];
if (midValue > target) {
end = mid - 1;
} else if (midValue < target) {
start = mid + 1;
} else {
find = true;
break;
}
}
if (find) System.out.println(1);
else System.out.println(0);
}
}
}