3.4. Softmax Regression

강의 링크 : https://d2l.ai/chapter_linear-networks/softmax-regression.html#equation-eq-l-cross-entropy

3.4. Softmax Regression

섹션 3.1에서는 선형 회귀를 도입하여 섹션 3.2의 처음부터 구현 작업을 수행하고 섹션 3.3의 딥 러닝 프레임워크의 고급 API를 사용하여 무거운 리프팅을 수행했다.

회귀는 how much? or how many?를 대답하고 싶을 때 우리가 도달하는 망치이다. 만약 여러분이 집이 팔릴 달러(가격) 수, 야구팀이 가질 수 있는 우승 횟수, 혹은 퇴원하기 전에 환자가 입원해 있는 일 수를 예측하고 싶다면, 여러분은 아마도 회귀 모델을 찾고 있을 것이다.

실제로, 우리는 classification을 더 살펴볼 것이다: "how much"가 아니라 "which one"을 묻는 것이다.

• Does this email belong in the spam folder or the inbox?
• Is this customer more likely to sign up or not to sign up for a subscription service?
• Does this image depict a donkey, a dog, a cat, or a rooster?
• Which movie is Aston most likely to watch next?

구어적으로, 기계 학습 실무자들은 두 가지 미묘하게 다른 문제를 설명하기 위해 단어 분류를 과부하한다. (i) categories (classes)에 대한 예제의 어려운 할당에만 관심이 있는 문제와 (ii) 각 범주가 적용될 확률을 평가하기 위해 soft한 할당을 원하는 문제이다. 구별이 모호해지는 경향이 있는데, 부분적으로는 우리가 어려운 과제에 신경을 쓸 때에도 여전히 soft한 과제를 만드는 모델을 사용하기 때문입니다.

3.4.1. Classification Problem

발을 젖게 하기 위해 간단한 이미지 분류 문제부터 시작해 보자. 여기서 각 입력은 $2\times2$ 회색조 이미지로 구성된다. 각 픽셀 값을 단일 스칼라로 표현할 수 있으며, $x_1, x_2, x_3, x_4$의 네 가지 특징을 제공한다. 또한 각 이미지가 “고양이”, “닭”및 “개”범주 중 하나에 속한다고 가정한다.

다음으로, 우리는 어떻게 labels을 표현할지 정해야한다. 우리는 두 가지 분명한 선택이 있다. 아마도 가장 자연스러운 선택은 $y \in {1, 2, 3}$를 선택하는 것이다. 여기서 정수는 각각 ${\text{dog}, \text{cat}, \text{chicken}}$를 나타낸다. 이러한 정보를 컴퓨터에 저장하는 좋은 방법이다. 카테고리들 사이에 자연스러운 순서가 있는 경우 (예: ${\text{baby}, \text{toddler}, \text{adolescent}, \text{young adult}, \text{adult}, \text{geriatric}}$을 예측하려는 경우) 이 문제를 회귀로 캐스팅하고 레이블을 이 형식으로 유지하는 것이 합리적일 수 있다.

그러나 일반적인 분류 문제는 클래스 간의 자연적인 순서와 함께 발생하지 않는다. 다행히 통계학자들은 오래 전에 범주형 데이터를 나타내는 간단한 방법인 one-hot encoding 을 발명했다. one-hot encoding은 카테고리 수만큼의 구성 요소를 가진 벡터로 특정 인스턴스의 범주에 해당하는 구성 요소는 1로 설정되고 다른 모든 구성 요소는 0으로 설정된다. 우리의 경우 레이블 $y$은 3 차원 벡터이며 $(1, 0, 0)$은 “고양이”에 해당하고 $(0, 1, 0)$는 “닭”에 해당하고 $(0, 0, 1)$는 “개”에 해당한다.

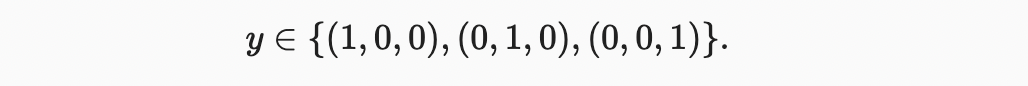
3.4.2. Network Architecture

가능한 모든 클래스에 대해 conditional probabilities(조건부 확률)을 추정하려면, 클래스 한개당 출력값이 여러 개인 모델이 필요하다. 선형 모델을 사용하여 분류를 처리하려면, 출력값만큼 많은 아핀 함수가 필요하다. 각 출력은 자체 아핀 함수에 해당한다. 이 경우 4 개의 features와 3 개의 가능한 출력 범주가 있으므로 가중치를 나타내는 12개의 스칼라 (아래 첨자가있는 $w$) 와 biases을 나타내는 3개의 스칼라 (아래 첨자가있는 $b$)가 필요하다.각 입력에 대해 다음 세 가지 logits($o_1, o_2$ 및 $o_3$)를 계산한다.

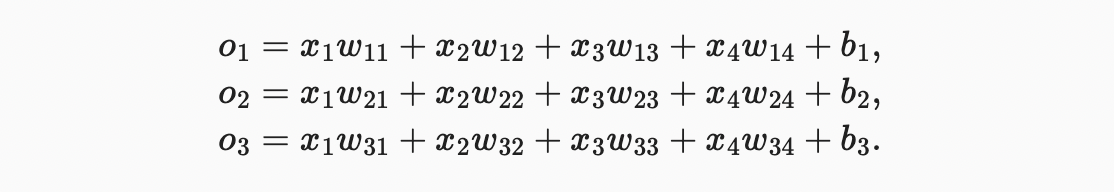
아래와 같이 신경망 다이어그램으로 이 계산을 묘사할 수 있다. 선형 회귀와 마찬가지로 소프트맥스 회귀도 단일 계층 신경망이다. 또한 각 출력값 $o_1, o_2$ 및 $o_3$의 계산은 모든 입력 ($x_1$, $x_2$, $x_3$ 및 $x_4$) 에 따라 달라지므로 소프트맥스 회귀의 출력 계층도 fully-connected layer로 설명할 수 있다.

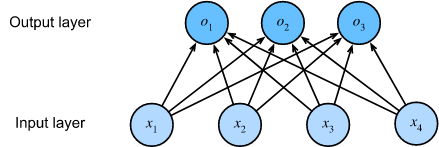
모델을 더 간결하게 표현하기 위해 선형대수 표기법을 사용할 수 있다. 벡터형식으로는 수학적 표기와 코드 작성에 더 적합한 양식 인 $\mathbf{o} = \mathbf{W} \mathbf{x} + \mathbf{b}$에 도달할 수 있다. 모든 가중치를 $3 \times 4$ 행렬로 수집했으며 주어진 데이터 예제 $\mathbf{x}$의 features에 대해 출력은 입력 특성과 편향 $\mathbf{b}$에 의해 가중치의 행렬-벡터 곱으로 제공된다.

3.4.3. Parameterization Cost of Fully-Connected Layers

다음 장에서 볼 수 있듯이 fully-connected layers는 딥 러닝에서 어디에나 있다. 그러나 이름에서 알 수 있듯이 완전 연결 계층은 잠재적으로 많은 학습 가능한 파라미터와 fully 연결된다. 특히, $d$입력 및 $q$출력이 있는 완전 연결 계층의 경우 파라미터화 비용은 $\mathcal{O}(dq)$이며, 이는 실제로 엄청나게 높을 수 있다. 다행스럽게도 $d$ 입력을 $q$ 출력으로 변환하는 이러한 비용을 $\mathcal{O}(\frac{dq}{n})$로 줄일 수 있다. 여기서 하이퍼 파라미터 $n$는 실제 응용 프로그램에서 매개변수 저장과 모델 효율성 간의 균형을 맞추기 위해 유연하게 지정할 수 있다.

3.4.4. Softmax Operation

여기서 중요한 점은 모델의 출력을 확률로 해석하는 것이다. 관측된 데이터의 가능성을 최대화하는 확률을 생성하기 위해 매개변수를 최적화할 것입니다. 그런 다음 예측을 생성하기 위해 threshold(임계 값)을 설정한다. 예를 들어 예측 확률이 최대인 레이블을 선택한다.

모든 출력 $\hat{y}_j$ 를 주어진 항목이 클래스 $j$에 속할 확률로 해석되기를 바란다. 그런 다음 출력 값이 가장 큰 클래스를 예측 $\operatorname*{argmax}_j y_j$로 선택할 수 있다.예를 들어 $\hat{y}_1$, $\hat{y}_2$ 및 $\hat{y}_3$이 각각 0.1, 0.8 및 0.1인 경우 (이 예에서는) “닭”을 나타내는 카테고리 2를 예측합니다.

선형 계층의 출력값을 바로 확률로 해석하는 데는 몇 가지 문제가 있다. 한편, 어떤 것도 이 숫자들을 1로 합하도록 제한하지 않는다. 반면, 입력에 따라 음의 값을 취할 수 있다. 이는 섹션 2.6에 제시된 확률의 기본 공리를 위반한다.

출력값을 확률로 해석하기 위해 (새로운 데이터에서도) 합이 음수가 아닌 1이라는 것을 보장해야 한다. 또한 모델이 확률을 충실히 추정하도록 권장하는 훈련 목표가 필요하다. 분류기가 0.5를 출력하는 모든 사례 중, 그러한 사례의 절반이 실제로 예측된 클래스에 속하기를 바란다. 이것은 calibration 이라고 불리는 속성이다.

softmax function는 정확히 이것을 한다. logits이 음이 아닌 1이 되고 합이 1이 되도록 변환하기 위해, 먼저 각 logits을 지수화한 다음(non-negativity 보장) 합으로 나눈다(합이 1이 되도록 함).

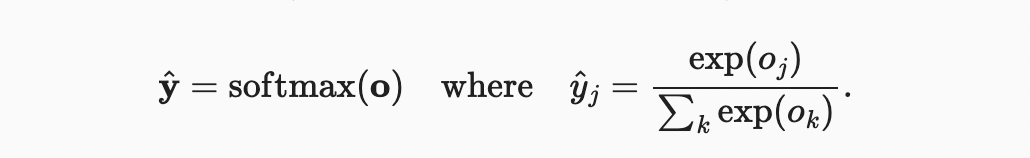
모든 $j$에 대해 $0 \leq \hat{y}_j \leq 1$에서 $\hat{y}_1 + \hat{y}_2 + \hat{y}_3 = 1$을 쉽게 볼 수 있다. 따라서 $\hat{\mathbf{y}}$는 요소 값을 적절히 해석할 수 있는 적절한 확률 분포입니다. 소프트맥스 연산은 단순히 각 클래스에 할당된 확률을 결정하는 소프트맥스 이전 값으로 logits $\mathbf{o}$ 간의 순서를 변경하지 않는다. 따라서 예측 중에 다음과 같이 가장 가능성이 높은 클래스를 선택할 수 있다.

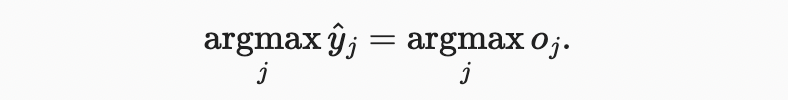
소프트맥스는 비선형 함수이지만 소프트맥스 회귀의 출력은 여전히 입력 형상의 아핀 변환에 의해 결정된다.

3.4.5. Vectorization for Minibatches

계산 효율성을 개선하고 GPU를 활용하기 위해 일반적으로 데이터의 미니 배치에 대한 벡터 계산을 수행한다. feature dimensionality (number of inputs) $d$ 및 batch size $n$가 있는 examples의 미니배치 $\mathbf{X}$이 주어진다고 가정하자. 또한 출력에 $q$개의 범주가 있다고 가정하자. 그런 다음 미니배치 feature $\mathbf{X}$가 $\mathbb{R}^{n \times d}$에 있고, 가중치는 $\mathbf{W} \in \mathbb{R}^{d \times q}$이며 bias은 $\mathbf{b} \in \mathbb{R}^{1\times q}$ 이다.

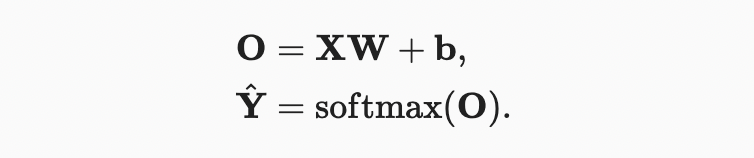
이것은 한 번에 하나의 예제를 처리하면 실행될 행렬-벡터 곱과 비교하여 행렬-행렬 곱 $\mathbf{X} \mathbf{W}$로의 지배적 연산을 가속화합니다. $\mathbf{X}$의 각 행은 데이터 예제를 나타내므로 소프트맥스 연산 자체를 rowwise 로 계산할 수 있다. $\mathbf{O}$의 각 행에 대해 모든 항목을 지수화한 다음 합계로 정규화한다. 위에서 합계 $\mathbf{X} \mathbf{W} + \mathbf{b}$ 동안 브로드캐스트를 트리거하는 경우, 미니배치 로짓 $\mathbf{O}$과 출력 확률 $\hat{\mathbf{Y}}$는 모두 $n \times q$ 행렬이다.

3.4.6. Loss Function

다음으로 예측된 확률의 품질을 측정하기 위해 손실 함수가 필요하다. 선형 회귀에서 평균 제곱 오차 목적에 대한 확률적 정당성을 제공할 때 접했던 것과 동일한 개념인 maximum likelihood estimation에 의존할 것이다.

3.4.6.1. Log-Likelihood

소프트맥스 함수는 벡터 $\hat{\mathbf{y}}$을 제공하며, 입력 $\mathbf{x}$ (예: $\hat{y}_1$ = $P(y=\text{cat} \mid \mathbf{x})$) 이 주어지면 각 클래스의 estimated conditional probabilities로 해석할 수 있다. 전체 데이터셋 ${\mathbf{X}, \mathbf{Y}}$에 $n$의 예제가 있다고 가정하자. 여기서 $i$로 인덱싱된 예제는 특징 벡터 $\mathbf{x}^{(i)}$과 원핫 레이블 벡터 $\mathbf{y}^{(i)}$로 구성된다. 다음과 같은 특징이 주어지면 실제 클래스가 모델에 따라 얼마나 가능한지 확인하여 추정치를 현실과 비교할 수 있다.

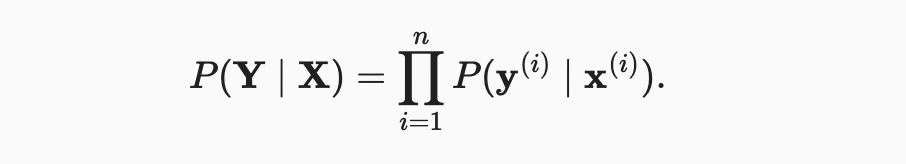
최대 likelihood 추정에 따르면 $P(\mathbf{Y} \mid \mathbf{X})$를 최대화하는데 이는 음의 로그 우도를 최소화하는 것과 같다.

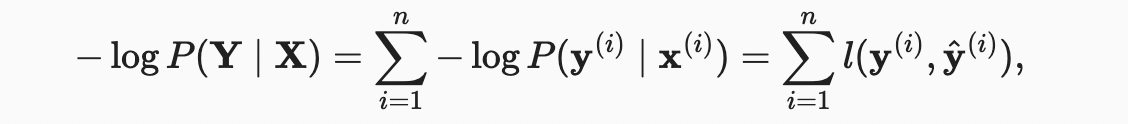
여기서 $q$ 클래스에 대한 레이블 $\mathbf{y}$ 및 모델 예측 $\hat{\mathbf{y}}$의 모든 쌍에 대해 손실 함수 $l$은 다음과 같다.

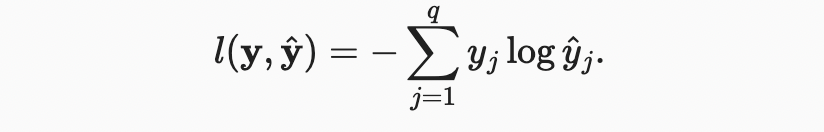
나중에 말하겠지만 위와 같은 식은 cross-entropy loss 라고 부른다. $\mathbf{y}$가 길이 $q$의 원핫 벡터이기 때문에, 모든 좌표 $j$에 대한 합은 한 항을 제외한 모든 항에서 사라진다. 모든 $\hat{y}_j$는 예측 확률이므로 로그는 $0$보다 크지 않다. 결과적으로 certainty로 실제 레이블을 올바르게 예측하면 손실 함수를 더 이상 최소화 할 수 없다. 즉, 실제 레이블 $\mathbf{y}$에 대한 예측 확률 $P(\mathbf{y} \mid \mathbf{x}) = 1$이면 손실 함수를 더 이상 최소화 할 수 없다.이는 종종 불가능하다. 예를 들어 데이터셋에 레이블 노이즈가 있을 수 있다(일부 예에서는 레이블이 잘못 지정될 수 있음). 입력 기능이 모든 예제를 완벽하게 분류하기에 충분한 정보가 없는 경우에도 가능하지 않을 수 있다.

3.4.6.2. Softmax and Derivatives

소프트맥스와 그에 상응하는 손실은 매우 흔하기 때문에 계산 방법을 조금 더 잘 이해할 가치가 있다.

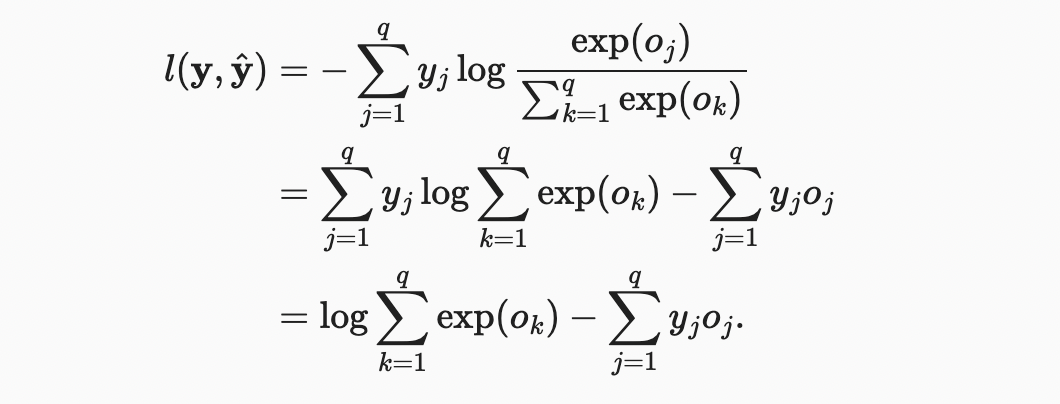
무슨 일이 일어나고 있는지 좀 더 잘 이해하려면 로짓 $o_j$에 대한 도함수를 고려하자.

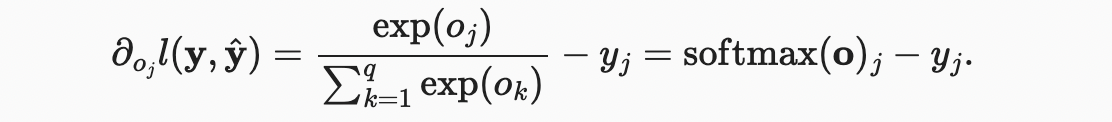
즉, 미분은 소프트맥스 연산으로 표현되는 모델에 의해 할당된 확률과 원핫 레이블 벡터의 요소로 표현된 실제 발생한 확률 간의 차이이다.이런 의미에서 기울기는 관측치 $y$와 추정치 $\hat{y}$의 차이인 회귀 분석에서 본 것과 매우 유사하다. 이것은 우연이 아니다. 지수 집합 모형에서 log-likelihood의 기울기는 정확하게 이렇게 지정된다.따라서 실제로 그래디언트를 쉽게 계산할 수 있다.

3.4.6.3. Cross-Entropy Loss

이제 단일 결과뿐만 아니라 결과에 대한 전체 분포를 관찰하는 경우를 생각해 보자. $\mathbf{y}$ 레이블에 이전과 동일한 표현을 사용할 수 있다. 유일한 차이점은 $(0, 0, 1)$과 같은 이진 항목만 포함하는 벡터가 아니라 이제 일반 확률 벡터 (예: $(0.1, 0.2, 0.7)$) 가 있다는 것이다. 이전에 손실 $l$을 정의하기 위해 사용했던 수학은 해석이 약간 더 일반적이라는 점에서 여전히 잘 작동한다. 레이블에 대한 분포에 대한 손실의 예상 값이다.이 손실을 cross-entropy loss 이라고하며 분류 문제에서 가장 일반적으로 사용되는 손실 중 하나이다.

3.4.7. Information Theory Basics

Information theory는 인코딩, 디코딩, 전송, 가능한 한 간결한 형태로 정보 (데이터라고도 함) 를 조작하는 것이다.

3.4.7.1. Entropy

정보 이론의 핵심 아이디어는 데이터의 정보 내용을 정량화하는 것이다. 이 수량은 데이터 압축 능력에 큰 제한을 둔다. 정보 이론에서 이 양을 분포 $P$의 entropy 라고 하며 다음 방정식으로 나타난다

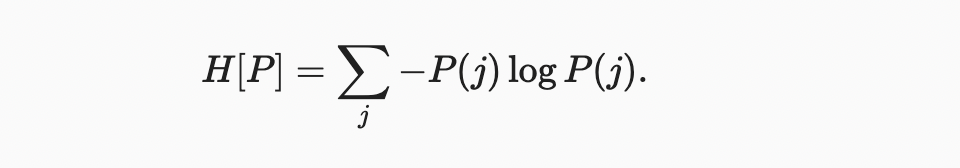
정보 이론의 기본 정리 중 하나는 분포 $P$에서 무작위로 추출한 데이터를 인코딩하기 위해 최소 $H[P]$ “nats”가 필요하다는 것이다. “nat”은 비트와 동일하지만 base 2가 아닌 base $e$의 코드를 사용하는 것이다. 따라서 하나의 nat는 $\frac{1}{\log(2)} \approx 1.44$비트이다.

3.4.7.2. Surprisal

3.4.7.3. Cross-Entropy Revisited

따라서 엔트로피가 실제 확률을 아는 사람이 경험하는 놀라움의 수준이라면, 교차 엔트로피가 무엇인지 궁금할 것이다. $H(P, Q)$로 표시되는 $P$에서 $Q$까지의 교차 엔트로피는 확률 $P$에 따라 실제로 생성된 데이터를 볼 때 주관적 확률 $Q$을 가진 관찰자의 예상되는 것이다. 가능한 가장 낮은 교차 엔트로피는 $P=Q$일 때이다. 이 경우 $P$에서 $Q$까지의 교차 엔트로피는 $H(P, P)= H(P)$이다.

요컨대, 교차 엔트로피 분류 목표는 두 가지 방식으로 생각할 수 있다. (i) 관찰 된 데이터의 가능성을 극대화하는 것; (ii) 레이블을 전달하는 데 필요한 놀라움 (따라서 비트 수) 을 최소화하는 것

3.4.8. Model Prediction and Evaluation

소프트맥스 회귀 모델을 훈련시킨 후, 어느 예제 기능이 주어져도 각 출력 클래스의 확률을 예측할 수 있다. 일반적으로 예측 확률이 가장 높은 클래스를 출력 클래스로 사용한다. 실제 클래스 (레이블) 와 일치하면 예측이 정확하다.

3.4.9. Summary

• The softmax operation takes a vector and maps it into probabilities.
• Softmax regression applies to classification problems. It uses the probability distribution of the output class in the softmax operation.
• Cross-entropy is a good measure of the difference between two probability distributions. It measures the number of bits needed to encode the data given our model.

3.4.10. Exercises