Image Classification은 입력 이미지를 받고 미리 정해놓은 label 카테고리가 존재해 컴퓨터는 이미지를 보고 어떤 카테고리에 속할지 분류해야하는 것이다. 하지만 우리가 이미지에 붙인 의미상의 레이블과 컴퓨터가 보는 픽셀값(숫자 집합) 사이에는 Semantic Gap이 존재한다. 또한 픽셀값들은 카메라의 위치를 바꾸거나 이미지상의 lllumination, Deformation, Occlusion 등과 같은 변형이 있어도 컴퓨터는 이를 구분할 수 있어야 한다.
시도된 방법 중 하나는 먼저 이미지에서 edges를 계산한 후 다양한 corners와 edges를 각 카테고리로 분류해 “explicit set of rule”을 써내려 가는 방법이다. 하지만 이런 알고리즘은 강인하지 않고, 또 다른 객체를 인식하려면 처음부터 다시 시작해야 해서 확장성이 없다는 문제가 있다. 그래서 다양한 객체들에게 유연하게 적용가능한 확장성 있는 알고리즘을 만들어야 한다.
이것들을 가능하게 하나의 통찰은 Data-Driven Approach이다. 손으로 직접 어떤 규칙을 써내려가는 것이 아닌, 인터넷에서 많은 데이터를 수집해 머신러닝 분류기를 통해 데이터를 잘 요약해서 다양한 객체들을 인식할 수 있는 모델을 만들어 내 새로운 이미지를 테스트 해보는 방식이다.
First Classifier: Nearest Neighbor
Train step에 모든 데이터를 기억하고 Predict step에서 가장 비슷한 이미지의 라벨을 예측하는 알고리즘이다. training은 O(1), prediction은 O(N)시간이 걸린다. 하지만 이와는 반대로 우리는 train 시간은 좀 느려도 되지만 test time에서는 빠르게 동작하는 알고리즘은 원한다.
Second Classifier: K-Nearest Neighbor
Distance Metric를 이용해 가까운 이웃을 k개만큼 찾고 이웃끼리 투표를 하는 방법으로 가장 많은 득표수를 획득한 레이블로 예측값을 낸다.
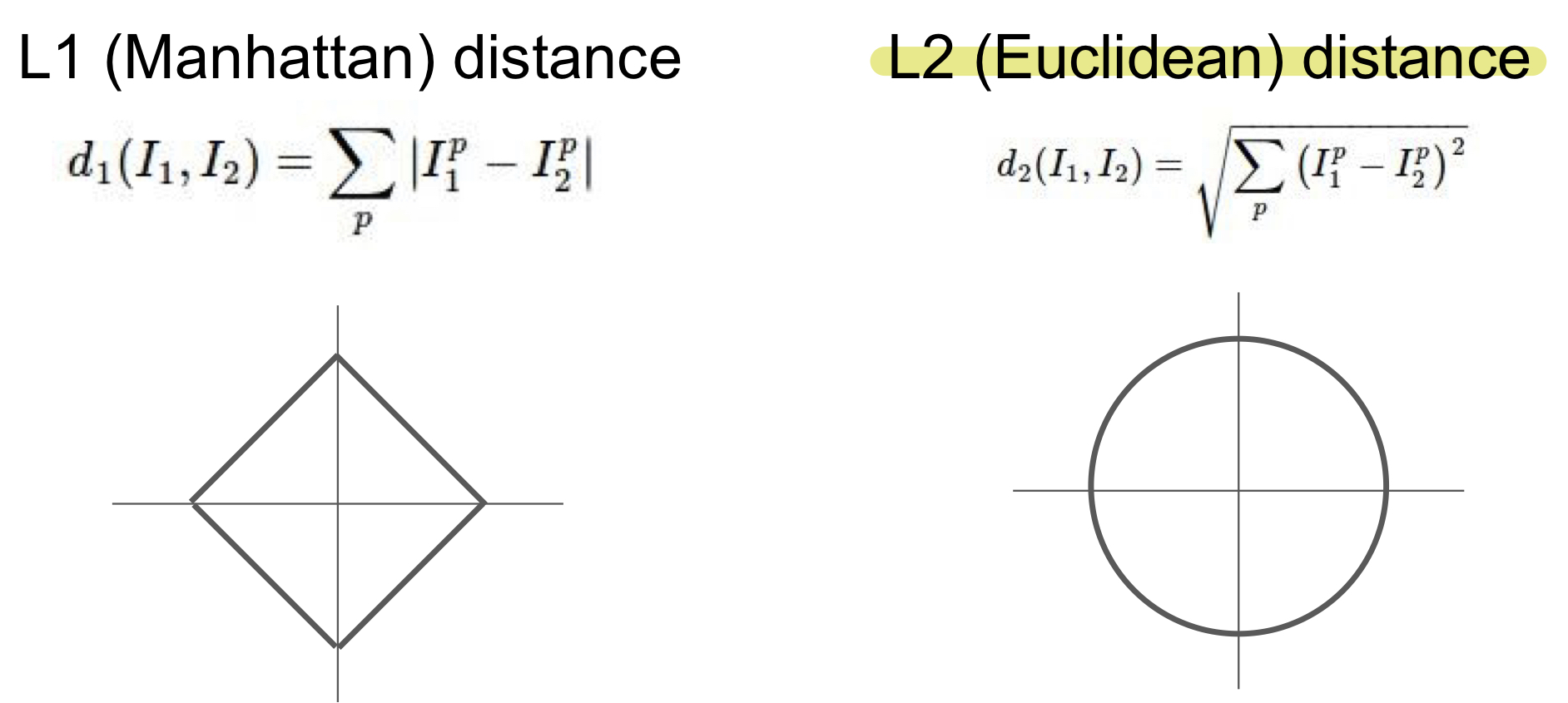
테스트 이미지 하나를 모든 학습 이미지들과 비교할 때 여러가지 비교 함수들이 있다. 두개의 차이점은 L1은 기존의 좌표계를 회전시키면 L1 distance가 변하지만 L2의 경우에는 좌표계와 연관이 없다. 그래서 만약 특징벡터의 각각 요소들이 개별적인 의미를 가지고 있다면(ex. 키, 몸무게) L1이 더 맞을 수 있고, 특징벡터가 일반적이고 요소들간 실질적인 의미를 잘 모르는 경우라면 L2가 더 어울릴 수 있다.
가장 좋은 k의 값을 무엇일까? 가장 좋은 distance는 무엇일까?
이런 k, distance들은 hyperparameters 들이다. 하이퍼 파라미터는 training시에 학습되는 것이 아니기 때문에 학습 전에 반드시 정해야 한다. 이 값들을 정하는 가장 간단한 방법은 데이터에 맞게 다양한 하이퍼파라미터 값들을 시도해보고 가장 좋은 값을 찾는 것이다.
하지만 “학습데이터”의 정확도와 성능을 최대화하는 하이퍼파라미터를 선택하는 것은 정말 끔찍한 방법이다. 왜냐하면 머신러닝에서는 학습데이터를 얼마나 잘 맞추는지는 중요하지 않고 우리가 학습시킨 분류기가 한번도 보지 못한 데이터를 얼마나 잘 예측하는지가 중요하기 때문이다.
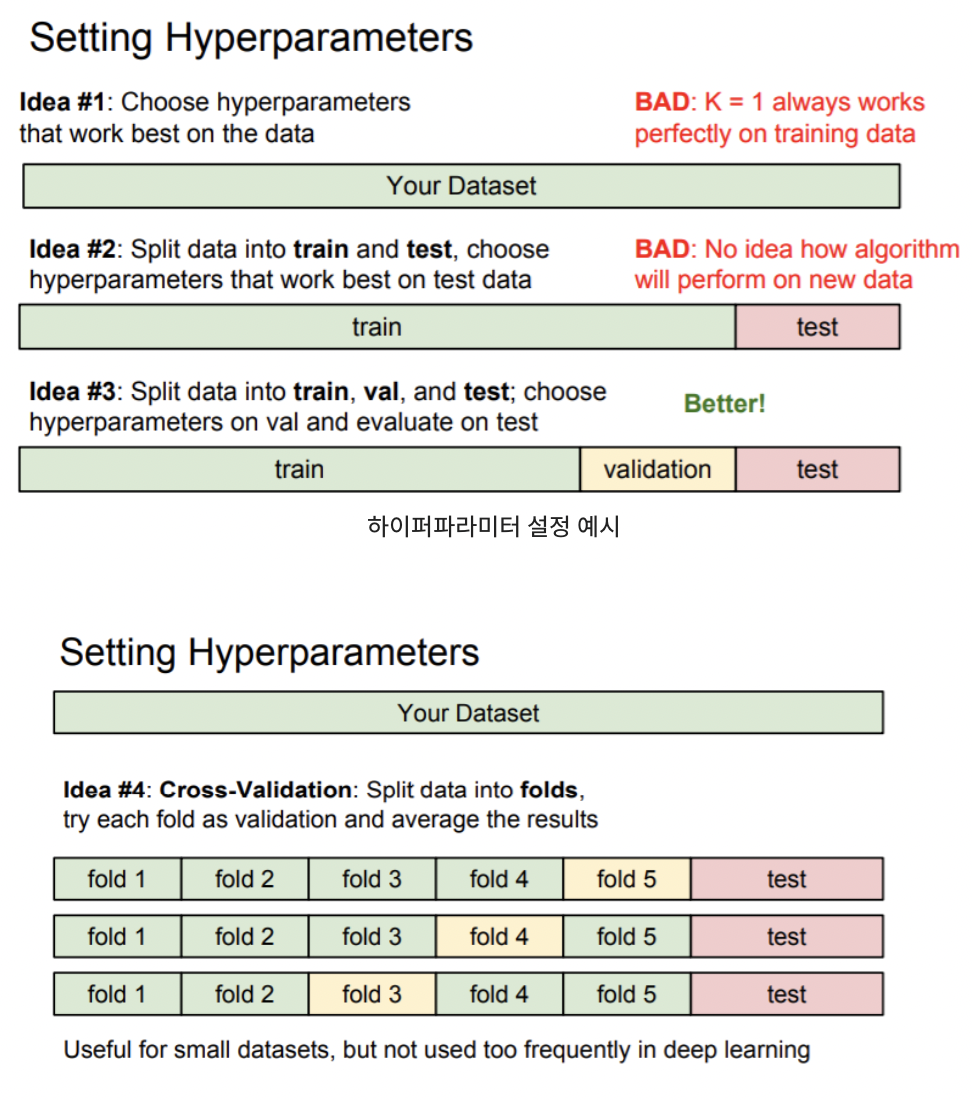
가장 일반적인 방법은 train & validation & test 로 나누는 것이다. 그리고 다양한 하이퍼파라미터로 train set을 학습시킨 후 validation set으로 검증을 한다. 여기서 가장 좋았던 하이퍼파라미터를 선택해 모든 사전작업을 마친 후에 test set에 한번만 수행을 한다.
다른 하이퍼 파라미터 선택으로는 Cross-Validation(교차 검증)이 있다. 이 방법은 작은 데이터셋일 경우 많이 사용된다. Test set을 만들어두고 나머지 데이터는 training set을 여러부분으로 나누고 번갈아가면서 validation set을 지정해 주는 방법이다.
사실 입력이 이미지인 경우에는 k-NN 분류기를 잘 사용하지 않는다. 첫번째 문제는 너무 느리다는 것이고 또 다른 문제는 L1/L2 Distance가 이미지간의 거리를 측정하는데 적절하지 않다는 점이다. 또 다른 문제로는 Curse of dimensionality가 있다. k-NN가 하는 일은 학습데이터를 이용해서 공간을 분할하는 것인데 이것이 잘 동작하기 위해서는 전체 공간을 덮을 정도의 충분한 데이터가 필요하다는 것을 의미한다. 만약 그렇지 않으면 neighbor이 아주 멀리 있어서 테스트 이미지를 제대로 분류할 수 없을 것이기 때문이다. 하지만 충분한 데이터양은 차원이 증가할수록 기하급수적으로 증가하기 때문에 이것은 매우 좋지 않다고 할 수 있다.
Linear classifier
Linear classifier는 Parametric model의 가장 단순한 형태로 뉴럴 네트워크의 기본요소이다. Parametric model에는 두개의 요소가 있는데 입력이미지 X와 가중치(or parameters) W(or theta) 이다. 그리고 함수 f(x, W)는 각 카테고리의 스코어인 n개의 숫자를 출력한다. 앞선 k-NN은 파라미터가 없고 전체 training set을 가지고 test time에 사용했다. 하지만
Parametric approach에서는 training 데이터의 정보를 요약해 요약된 정보를 파라미터 W에 모아준다. 이런 방식을 사용하면 test time에서 더이상 트레이닝 데이터가 필요하지 않고 파라미터 W만 필요하다. 이런 방식은 핸드폰같은 작은 장치에서 모델 동작시 효율적이다. 그래서 딥러닝은 바로 이 함수 f의 구조를 적절하게 잘 설계하는 일이라고 할 수 있다.
가중치 W와 데이터 X를 조합하는 가장 쉬운 방법은 둘을 곱하는 것이고 이 방법이 Linear Classifier이다. f(x, W = Wx) 입력이미지 32 x 32 x 3을 펴서 열벡터로 만들면 3072-dim 벡터가 된다. 이 벡터가 10개의 클래스로 되야하기 때문에 W는 10 x 3072행렬이 된다. 여기서 Bias term은 입력과 직접 연결되지 않으며 대신에 데이터와 무관하게 어떤 특정한 클래스에 우선권을 부여한다. 가령 데이터셋이 불균형한 상황에서 예를 들어 고양이 데이터가 개 데이터보다 훨씬 많은 상황이면 고양이 클래스에 상응하는 bias가 더 커지게 된다.
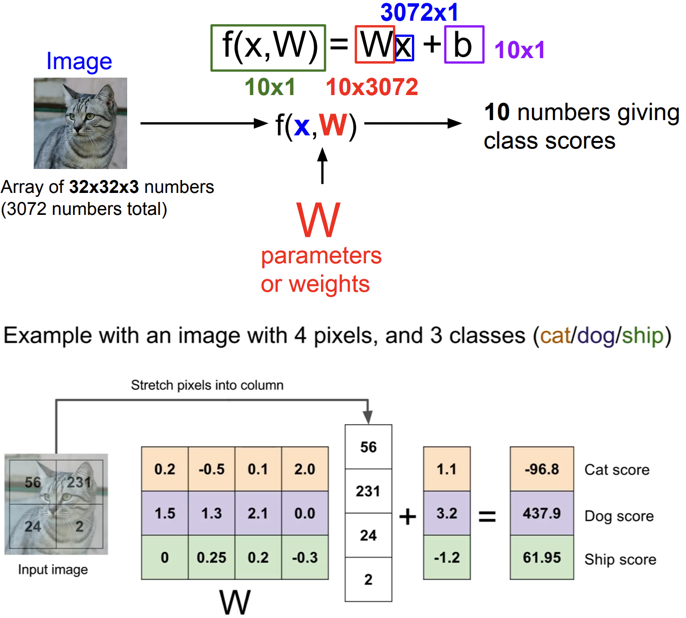
위를 보면 “고양이 스코어”는 입력이미지의 픽셀 값과 가중치(W) 행렬을 내적한 값에 bias를 더한 것이다. 이런 관점에서 Linear Classification은 template matching과 유사하다. W 행렬의 각 행은 각 이미지에 대한 template으로 볼 수 있고 벡터들간의 내적은 클래스 간 템플릿의 유사도를 측정하는 것과 유사하다. 여기서 bias는 데이터와 독립적으로 각 클래스에 scailing offsets을 더해주는 것이다.
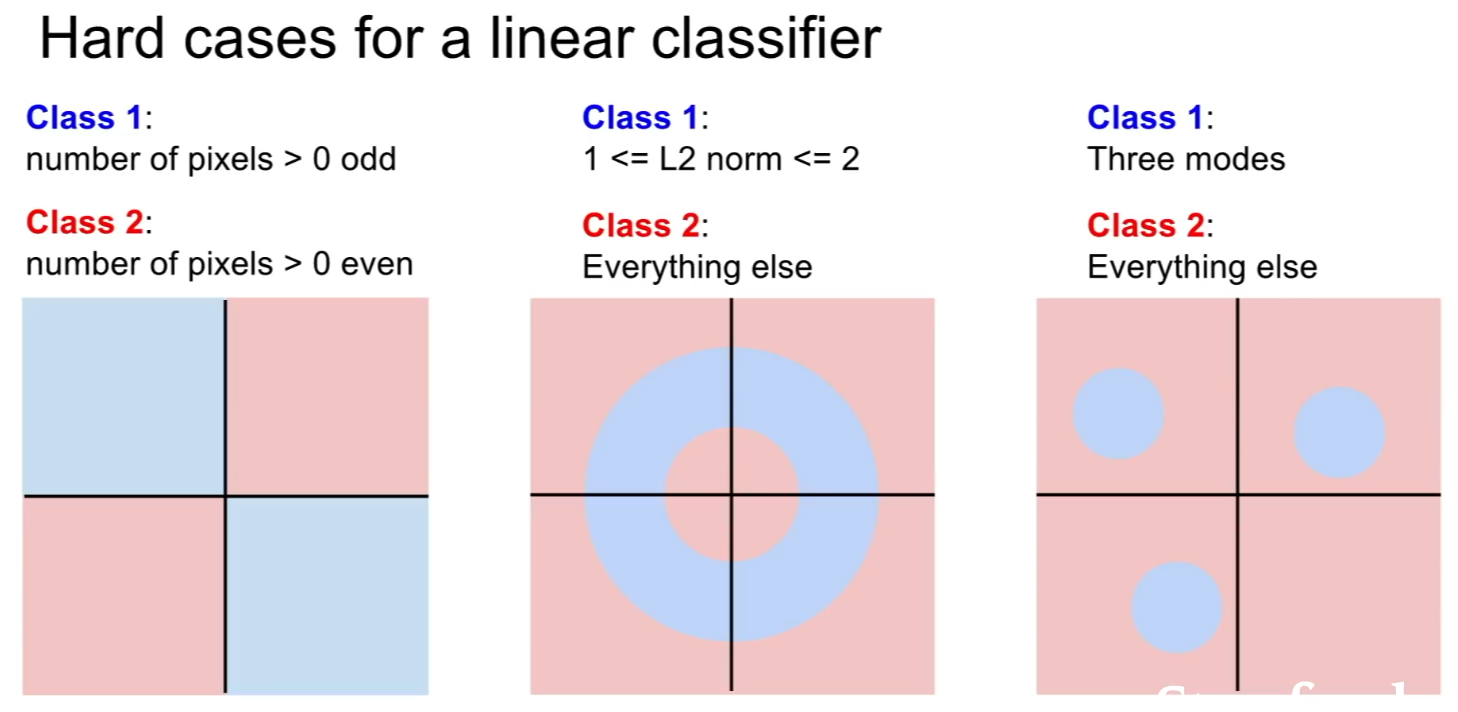
하지만 Linear classifier의 문제 중 하나는 각 클래스에 대해 하나의 템플릿만 학습한다는 것이다. 한 클래스 내에 다양한 특징들이 존재할 수 있지만, 모든 것을 평균화 시키기 때문에 각 카테고리를 인식하기 위한 템플릿은 하나밖에 없다.
또한 linear classifier가 다루기 어려운 문제들도 있다. 아래 그림들은 두 부분을 구별하는 선형 직선을 그릴 수 없는 걸 알 수 있다.