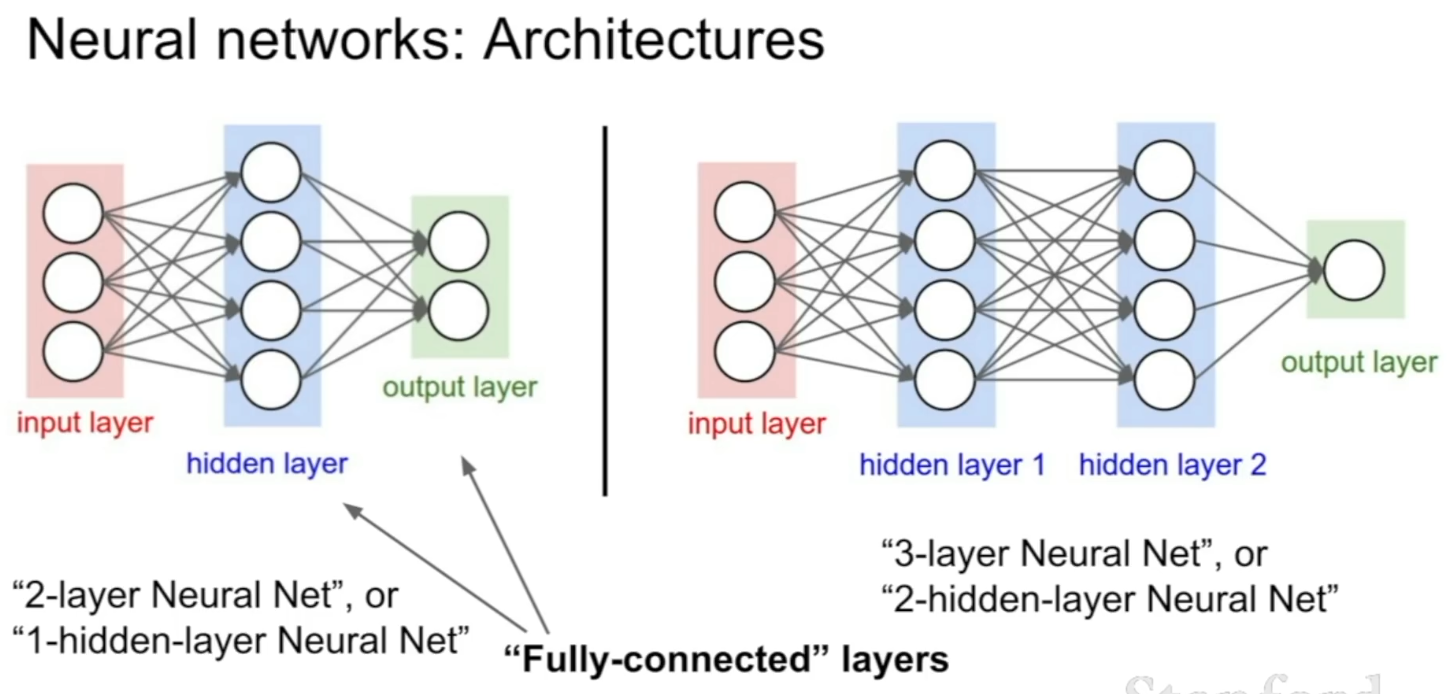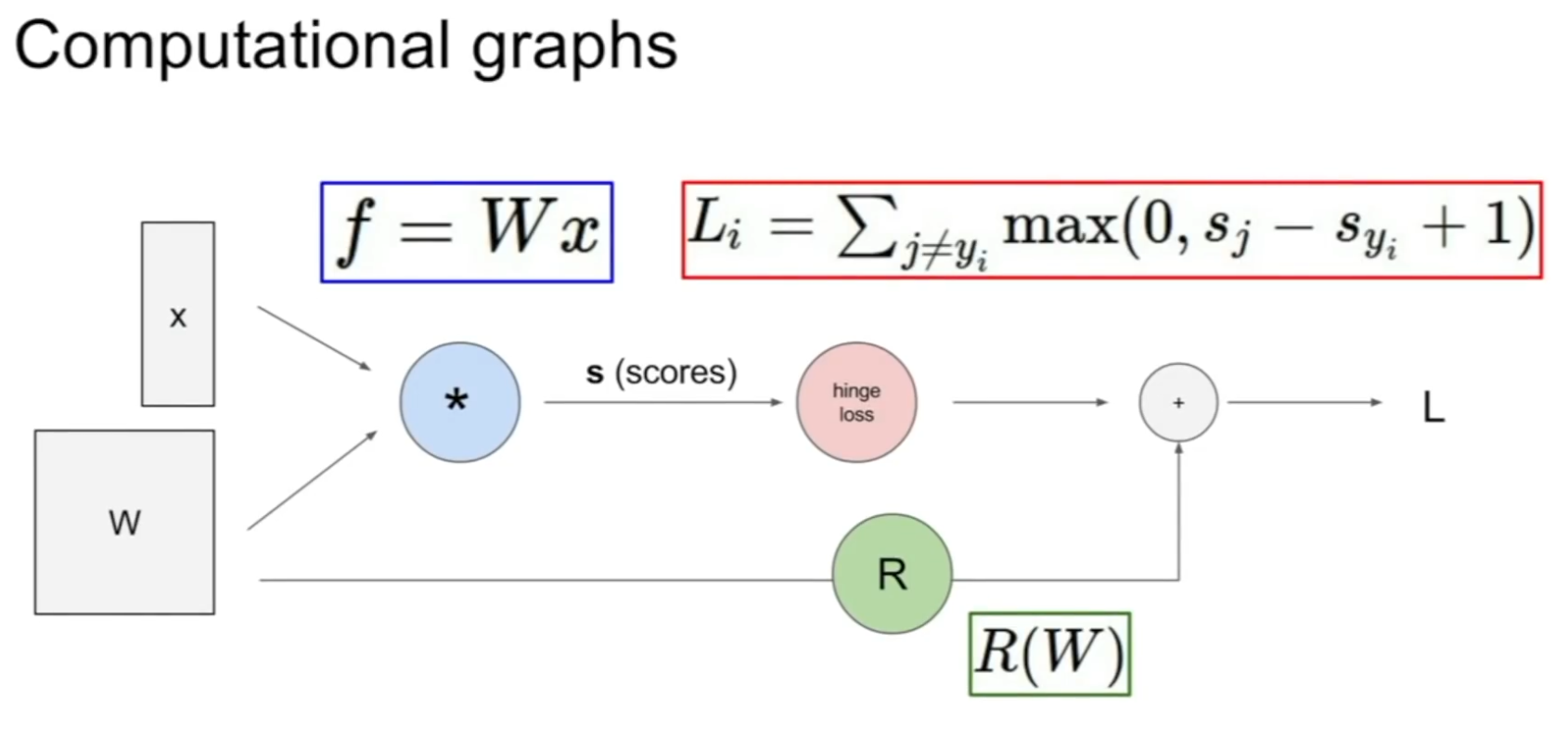
Computational graphs
Computational graphs를 이용해서 어느 함수든 표현할 수 있다.
예를 들어 아래는 지금까지 봤던 input이 인 linear classifier이다.
Backpropagation
이 computational graph를 이용해 함수를 표현하면 backpropagation을 사용할 수 있다.
역전파는 gradient를 얻기 위해 computational graph내부의 모든 변수에 대해 chain rule을 재귀적으로 사용한다.
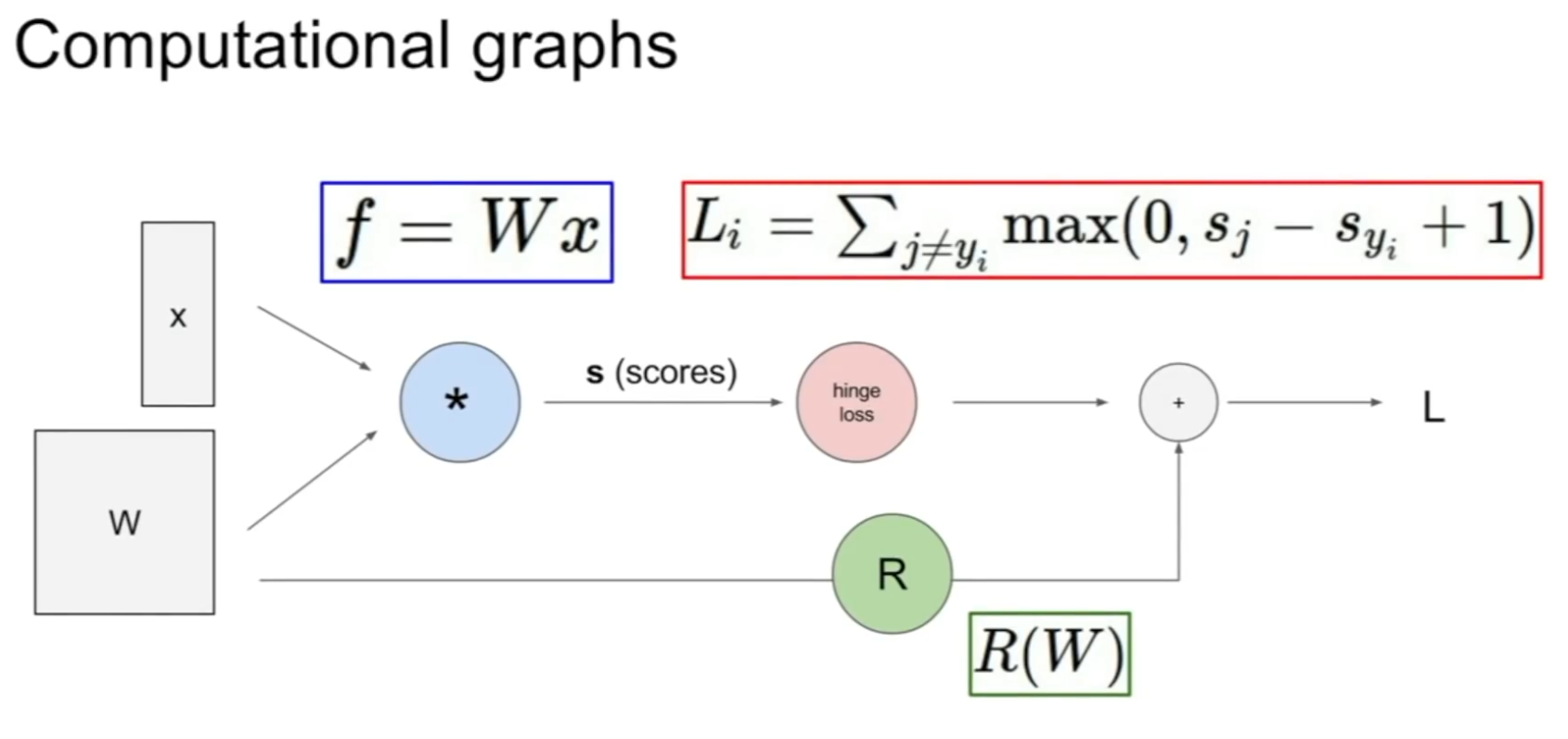
간단한 Backpropagation 예제를 살펴보자.
함수가 있고 라고 해보자.
각각의 수식에 이름을 붙여 로 설정하면 각각에 대한 미분값을 구할 수 있다.
우리가 찾기 원하는 것은 각각에 대한 의 gradient 값이다. 뒤에서부터 gradient를 계산해보자.
- 출력 f에 대한 gradient는 1
- 에 대한 의 gradient는 값이기 때문에 3
- 에 대한 의 gradient는 값이기 때문에 -4
- Chain rule을 이용해서 에 대한 의 gradient을 찾을 수 있다 → -4
- Chain rule을 이용해서 에 대한 의 gradient을 찾을 수 있다 → -4
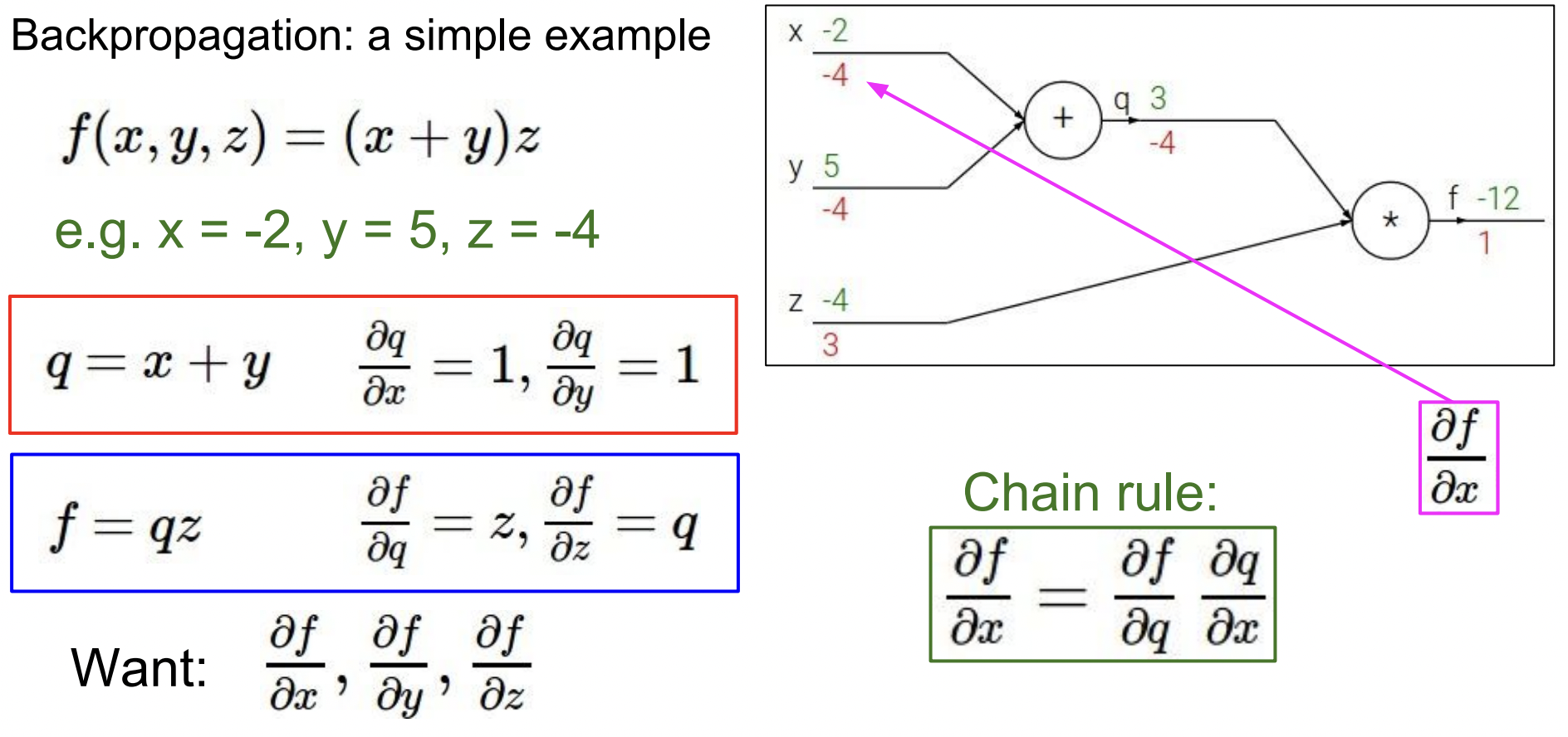
아래 그림을 보면 입력은 와 이고 출력은 이다. 여기서 우리는 local gradient인 와 각각에 대한 의 미분값을 계산할 수 있다. 이 값은 각 입력에 대한 출력의 기울기이다.
이제 backpropagation이 어떻게 동작하는지 봐보면 먼저 그래프 뒤에서부터 시작 부분까지 진행된다.
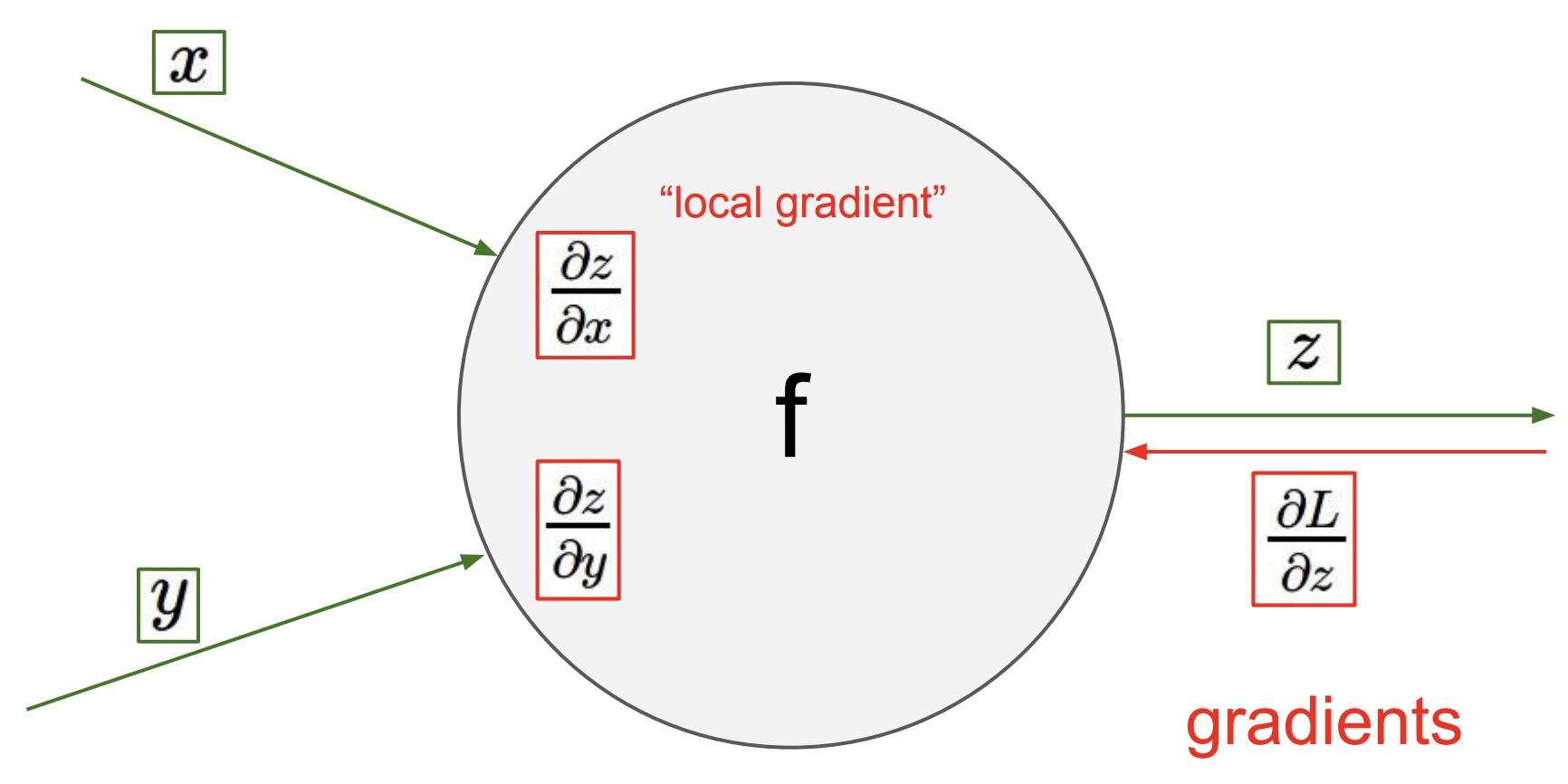
각 노드에 도착하면 출력과 관련된 노드의 gradient가 윗부분 노드로 ‘전차’된다. (backpropagation에서 해당 노드에 도달할 때까지 에 대한 최종 loss L은 이미 계산되어 있다.)
이제 우리는 와 값에 대한 바로 직전 노드의 gradient를 찾기 위해 chain rule을 사용한다.
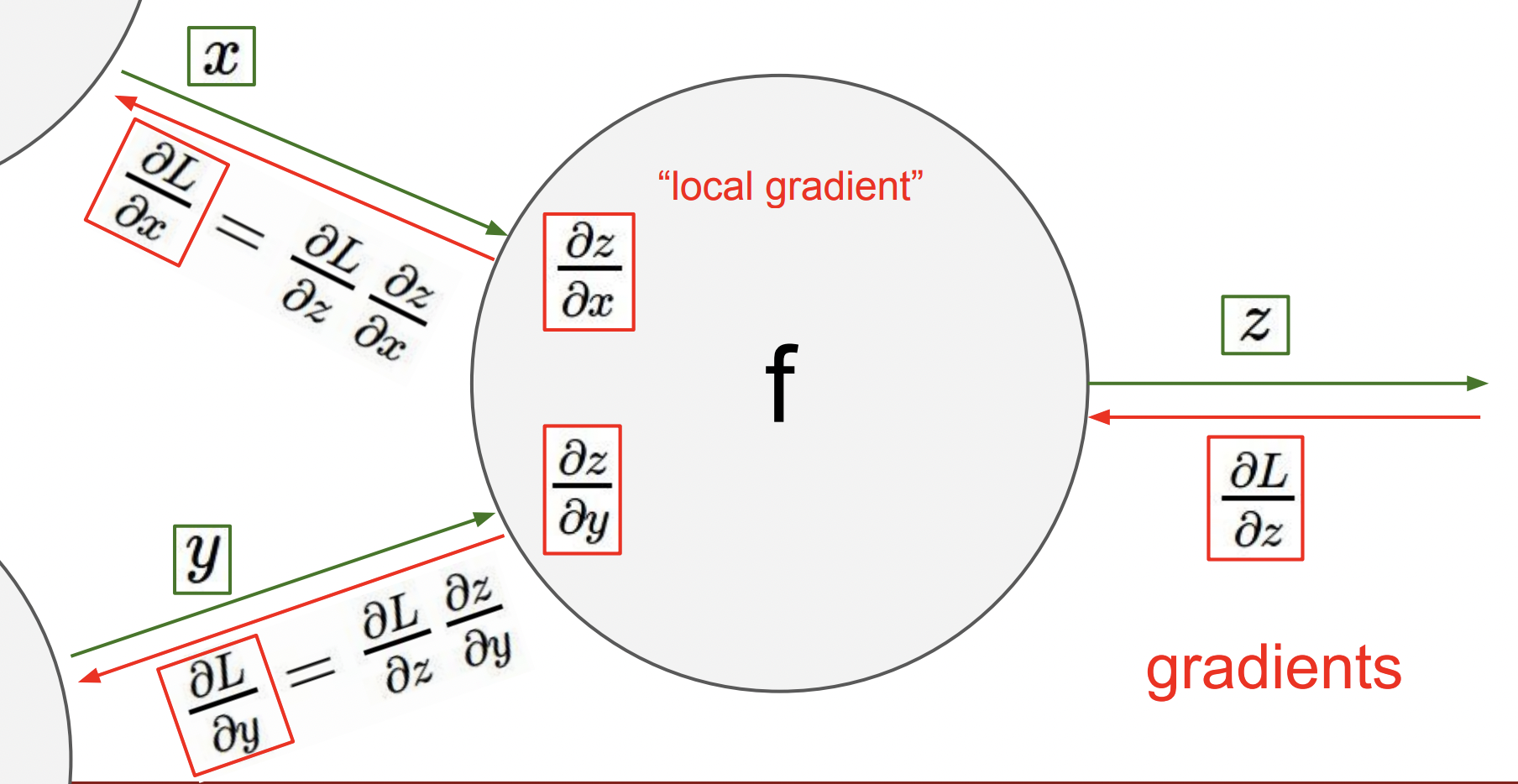
여기서 중요한 점은 각 노드가 우리가 계산한 local gradient를 가지고 있고 backpropagation을 통해 local gradient를 넘겨주면 그 값들은 상위 노드 방향으로 계속 전달되고 이제 이 값을 local gradient와 곱하기만 하면 된다는 것이다. 여기서 우리는 노드와 연결된 것 이외의 다른 값들은 신경쓰지 않아도 된다.
이제 좀더 복잡한 예제를 살펴보고 backpropagation의 유용성을 봐보자.
먼저 아래와 같이 함수 를 computational graph로 나타내고 임의의 값을 할당했다.
이제 backpropagation을 진행하기 위해 그래프의 맨 뒤에서부터 시작한다. 최종 변수에 대한 출력의 gradient는 1이다. 이제 local gradient를 찾아야 하는데 에 대한 local gradient는 아래와 같이 계산될 수 있고 이 변수에 대한 최종 gradient는 -0.53 값을 얻는다.
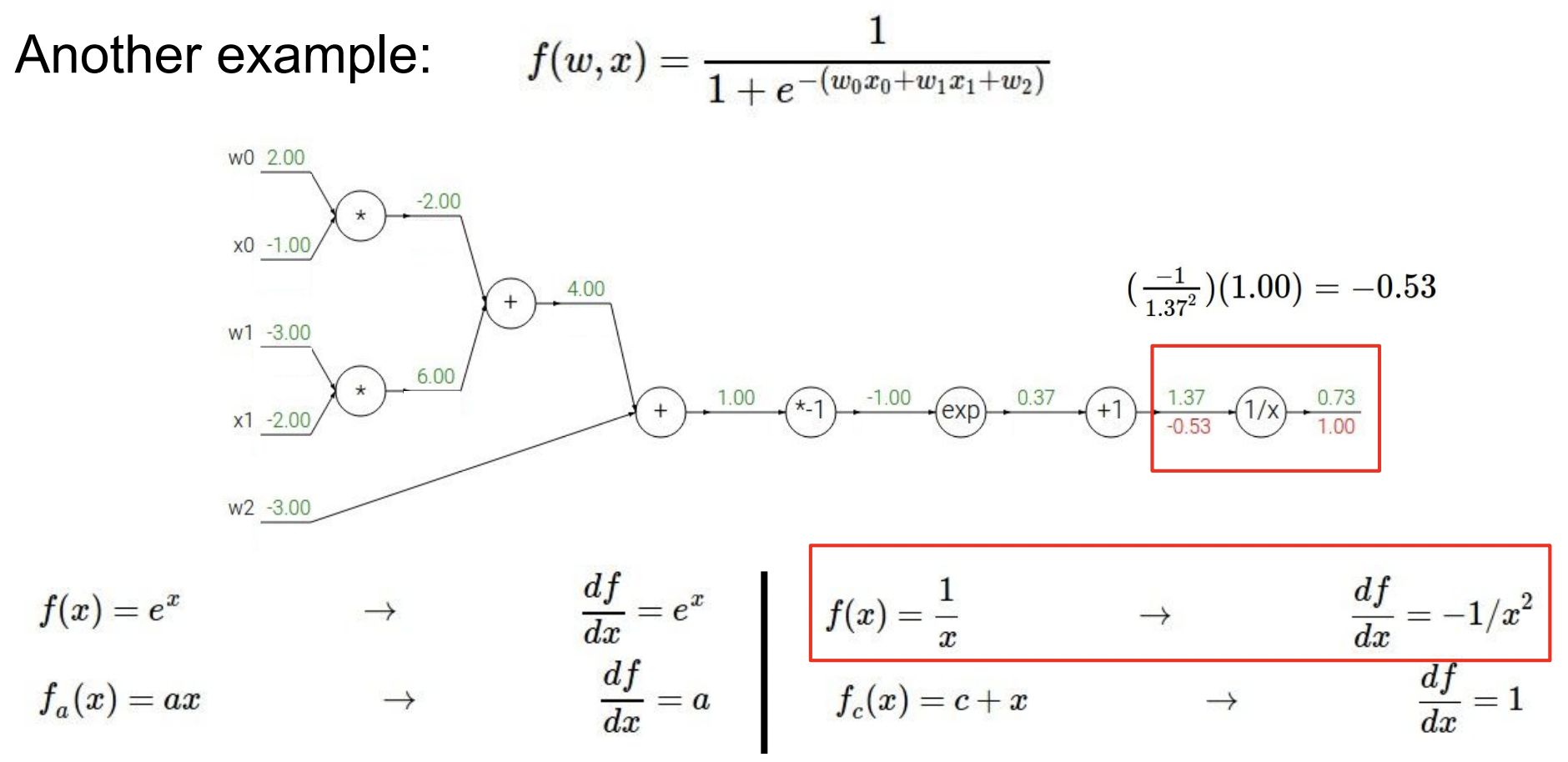
다음 노드로 넘어가 계산하면 동일한 동작을 진행하고 이것을 계속 반복한다.
이제 우리는 아래와 같이 노드 두개와 연결되어 있는 덧셈() 노드에 도달했다. Upstream gradient는 0.2이고 각 브랜치에 대한 gradient를 추가하면 둘다 0.2값을 얻는다. (덧셈 노드에서 입력에 대한 local gradient는 1)
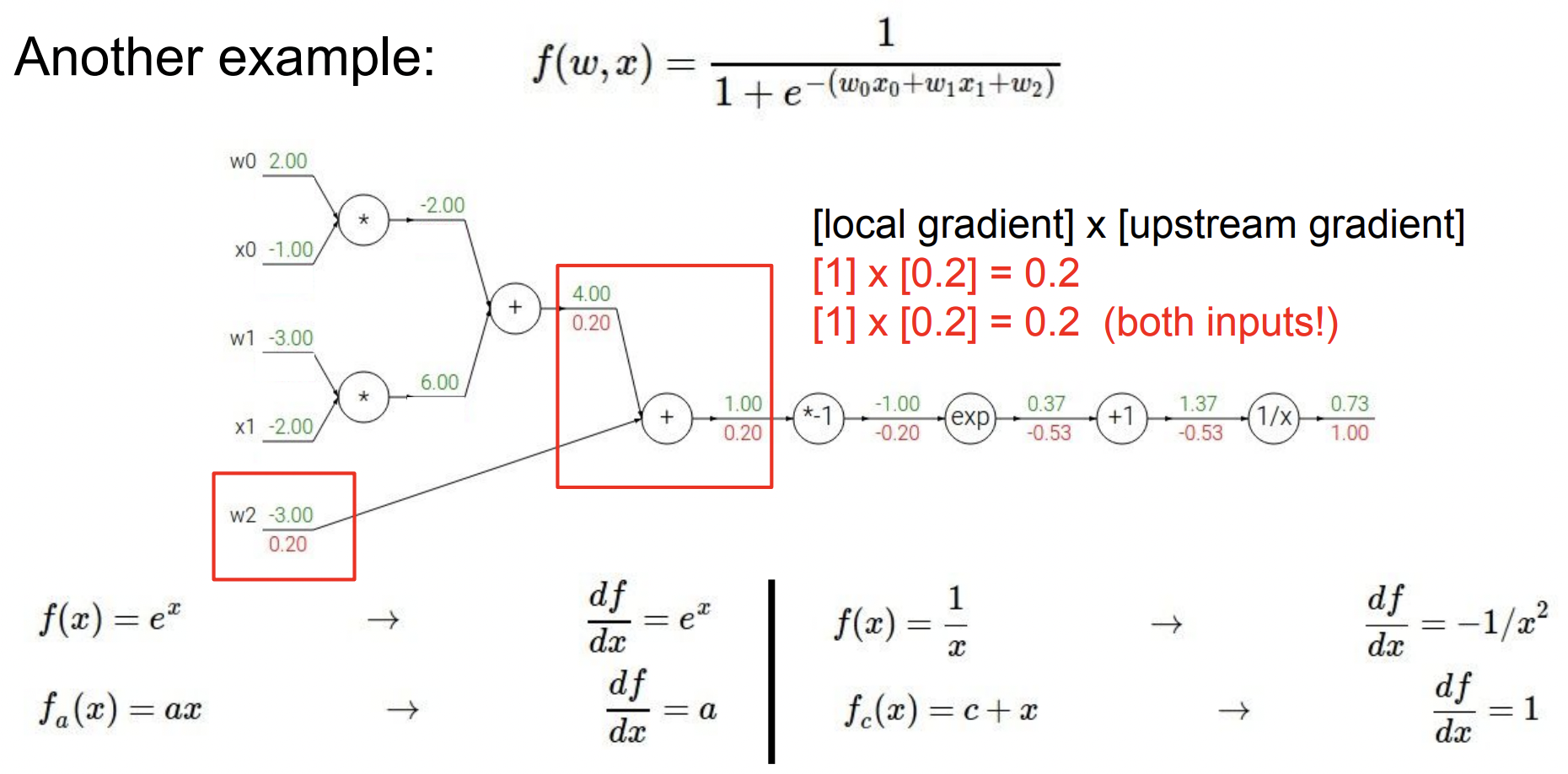
과 은 곱셈 노드를 가지고 있다. Upstream gradientsms 0.2로 아래와 같은 gradient 값을 얻게 된다. (곱셈 노드에서 각 입력에 대한 local gradient는 서로의 값)
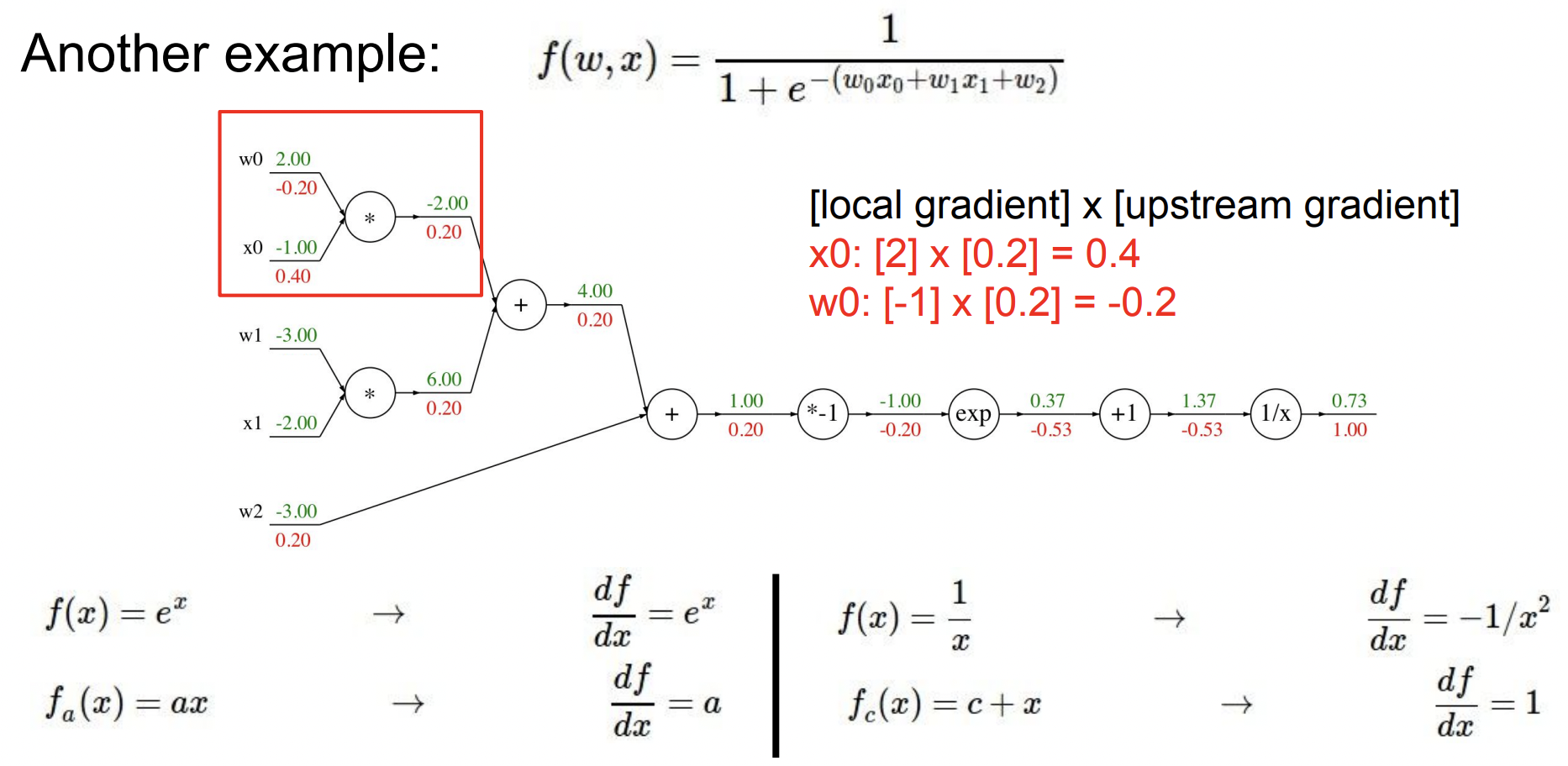
우리는 computational graph를 만들 때, computational 노드에 대해 우리가 원하는 세분화된 정의를 할 수 있다. 위 예제에서는 쉽고 단순한 것으로(, 등) 묶었지만 실제로 원한다면 더 복잡한 그룹으로 묶어 그 노드에 대한 local gradient를 적을 수 있다.
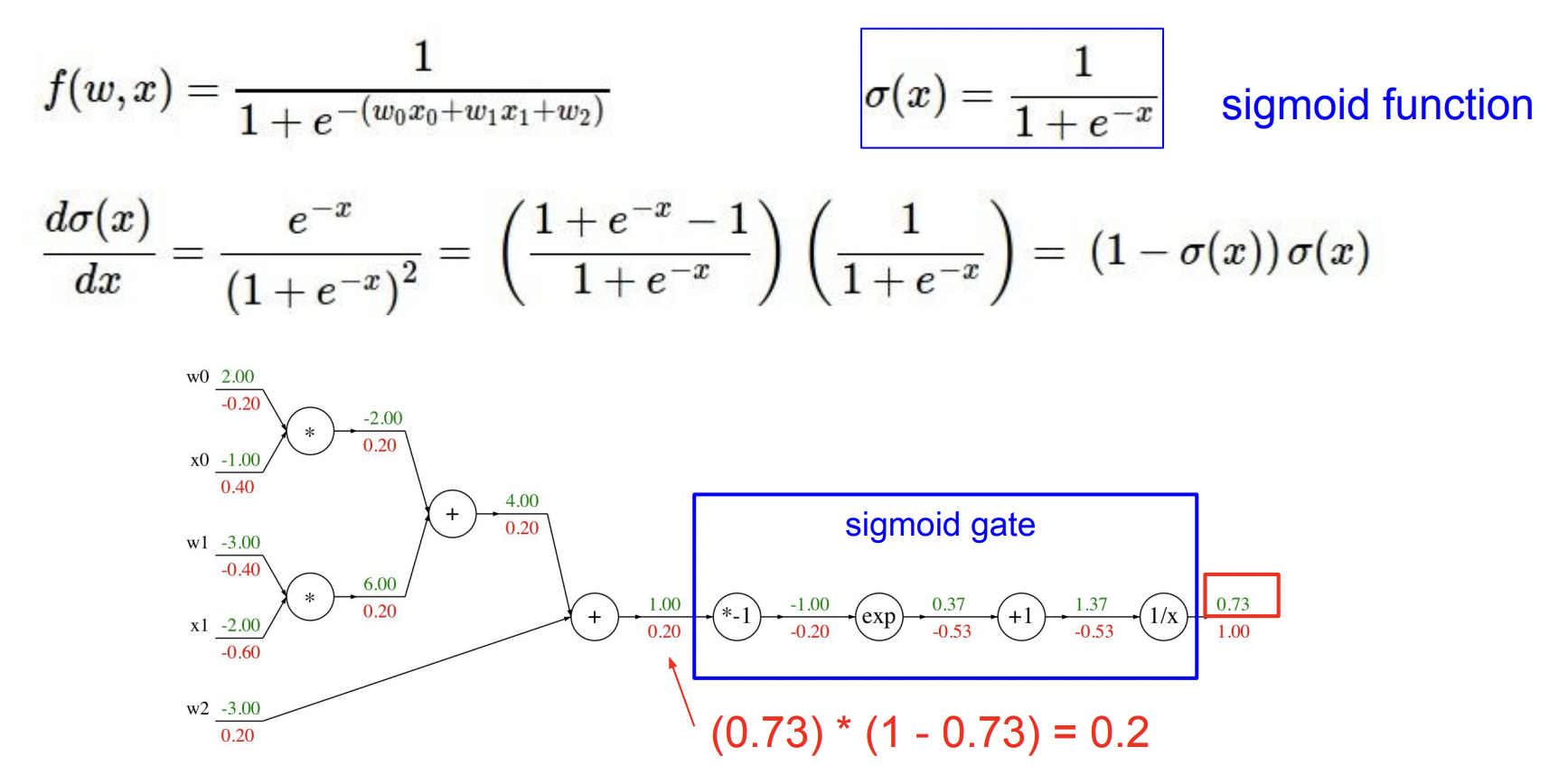
예를 들어 앞으로 자주 보게 될 sigmoid function을 아래 적어놓았다. 우리는 이 식에 대한 gradient를 계산할 수 있고 전개해보면 를 얻을 수 있다.
아래 그래프에서 sigmoid를 만들기 위한 부분을 찾을 수 있고 이 부분을 하나의 큰 노드, sigmoid로 바꿀 수 있다. (우리는 파란색 박스 sigmoid gate의 local gradient, operation, 에 대한 sigmoid 미분값을 모두 알고있다.)
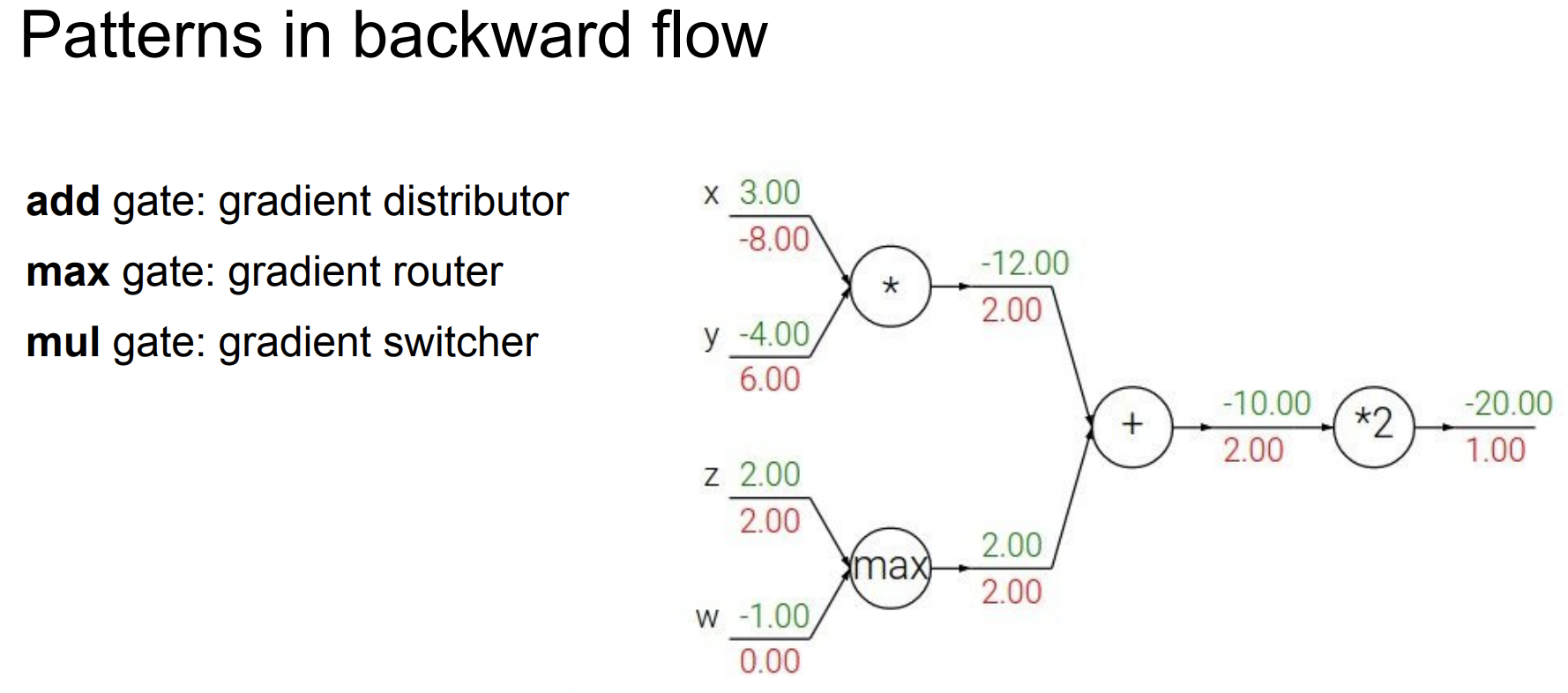
위에서 봤던 예제들을 살펴보면 아래와 같은 패턴을 찾을 수 있다. (아래 max gate에서 forward pass 를 생각해볼때 함수에 의미가 있는 값은 max(여기서는 2) 값 뿐이기 때문에 backward에서도 해당 계산에 대한 gradient만 값이 있는 것을 볼 수 있다.)
이제 스칼라 변수가 아닌 vector의 경우를 생각해보면 다른 모든 흐름은 같겠지만 이제 우리 gradient는 Jacobian matrix가 된다. Jacobian 행렬의 각 행은 입력에 대한 출력의 편미분이 될 것이다.
- Q1. What is the size of the size of the Jacobian matrix? [4096 x 4096]
- Q2. What does it look like? Diagonal Matrix 요소별(elementwise)이기 때문에 입력의 각 요소, 첫번째 차원은 오직 출력의 해당 요소에만 영향을 준다. 그렇기 때문에 우리의 Jacobian 행렬은 대각행렬(Diagonal Matrix)이 된다.

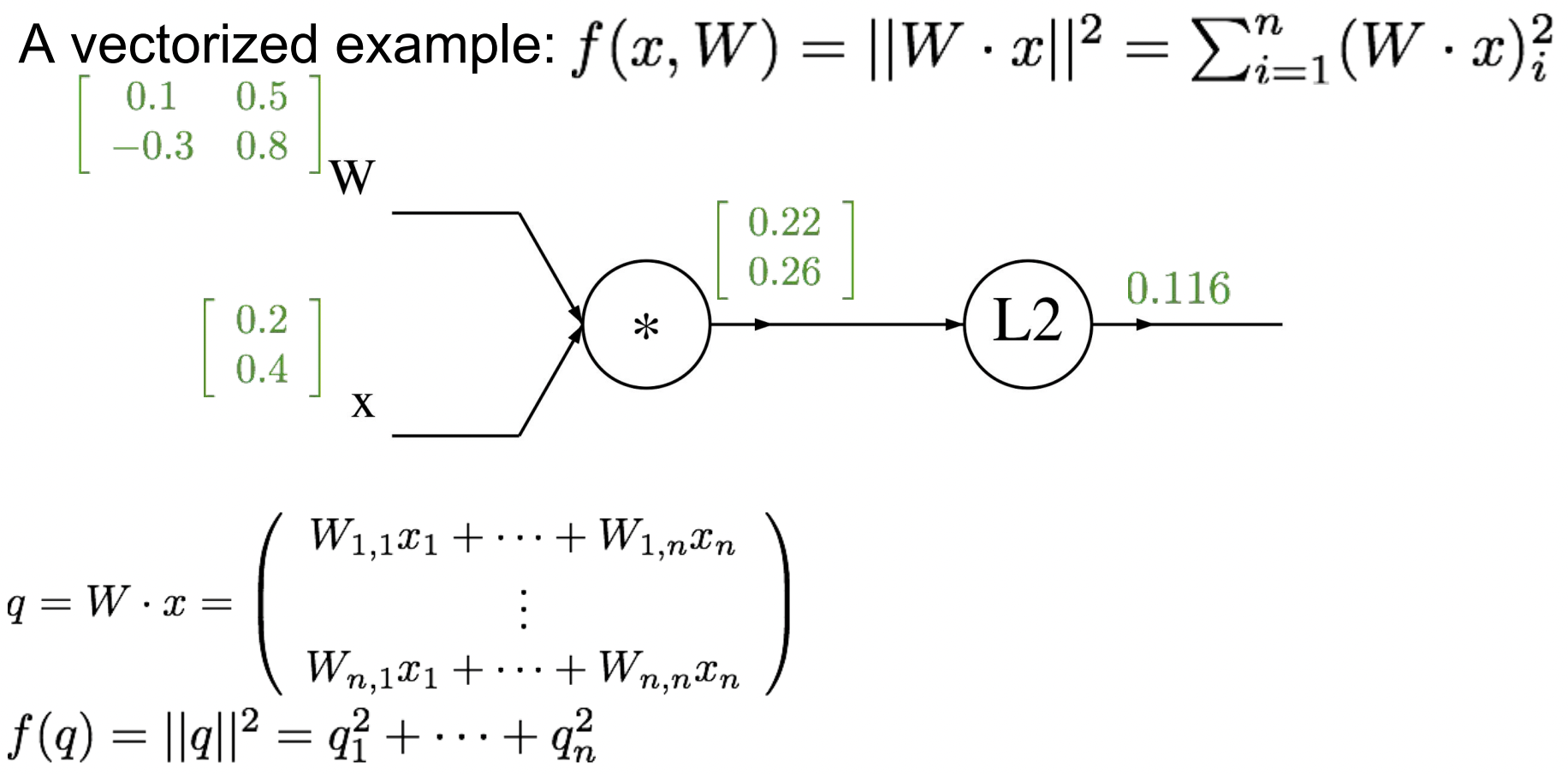
이제 좀 더 구체적으로 vectorized된 예시를 살펴보자. 함수 f(x, W)에 대해
이다. 여기서 함수 를 에 대한 표현으로 나타낼 수 있다. (의 두번째 노드를 보면 이것은 과 의 합으로 norm이다.)
아래와 같이 각각의 입력에 임의의 행렬을 대입하면 이제 와 최종 출력을 구할 수 있다.
이제 Backpropagation을 해보자❗️
-
출력에 대한 gradient 는 1
-
한 노드 뒤로 가서 이제 이전의 중간 변수인 (2차원 벡터)에 대한 gradient를 찾는다. 아래 수식에서 에 대한 의 gradient를 구할 수 있다. 이것은 벡터 에 2를 곱한 것이기 때문에 gradient 행렬을 구할 수 있다
- 벡터의 gradient는 항상 원본 벡터의 사이즈와 같고, gradient의 각 요소는 함수의 최종 출력에 얼마나 특별한 영향을 미치는지를 의미한다.
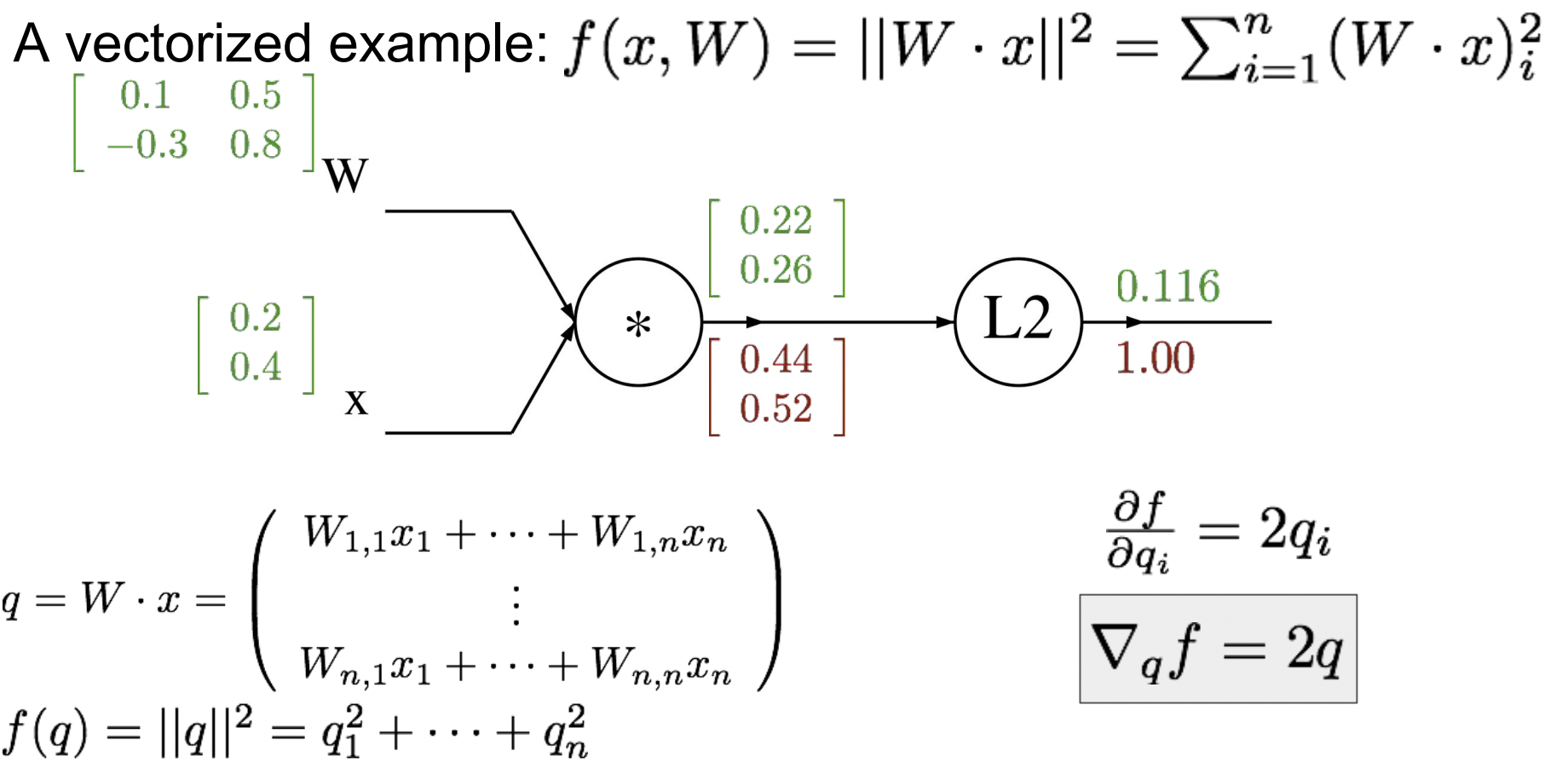
-
이제 한 노드 뒤로 가서 chain rule을 사용해 W의 gradient를 구하자. →
(오른쪽 상단에 유도된 식을 벡터화된 형식으로 표현했다.)
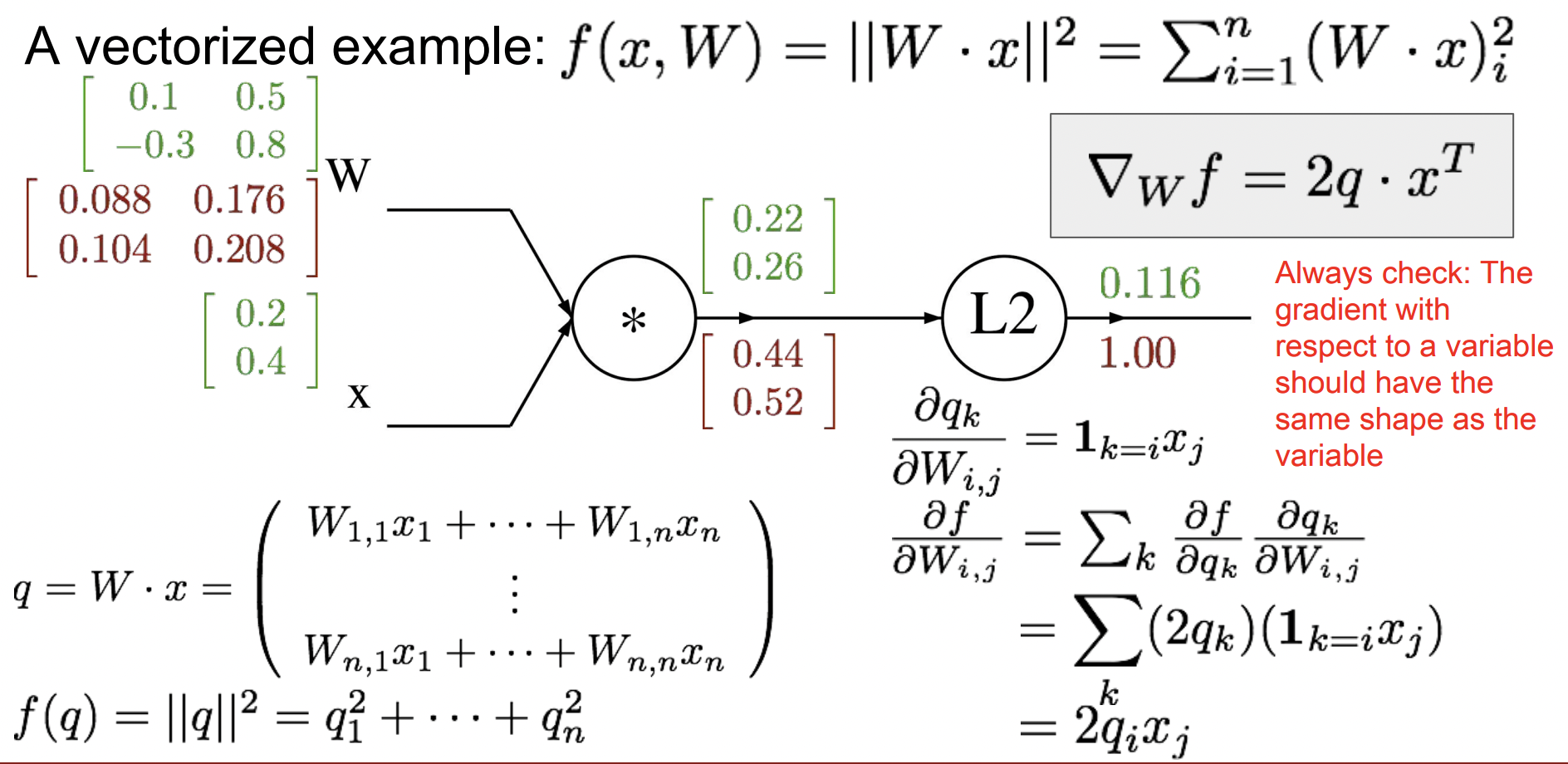
- 마지막으로 x의 gradient를 구하자. →
(이것은 와 같은 모양을 가질 것이고 오른쪽 상단에 유도된 식을 벡터화된 형식으로 표현했다. )
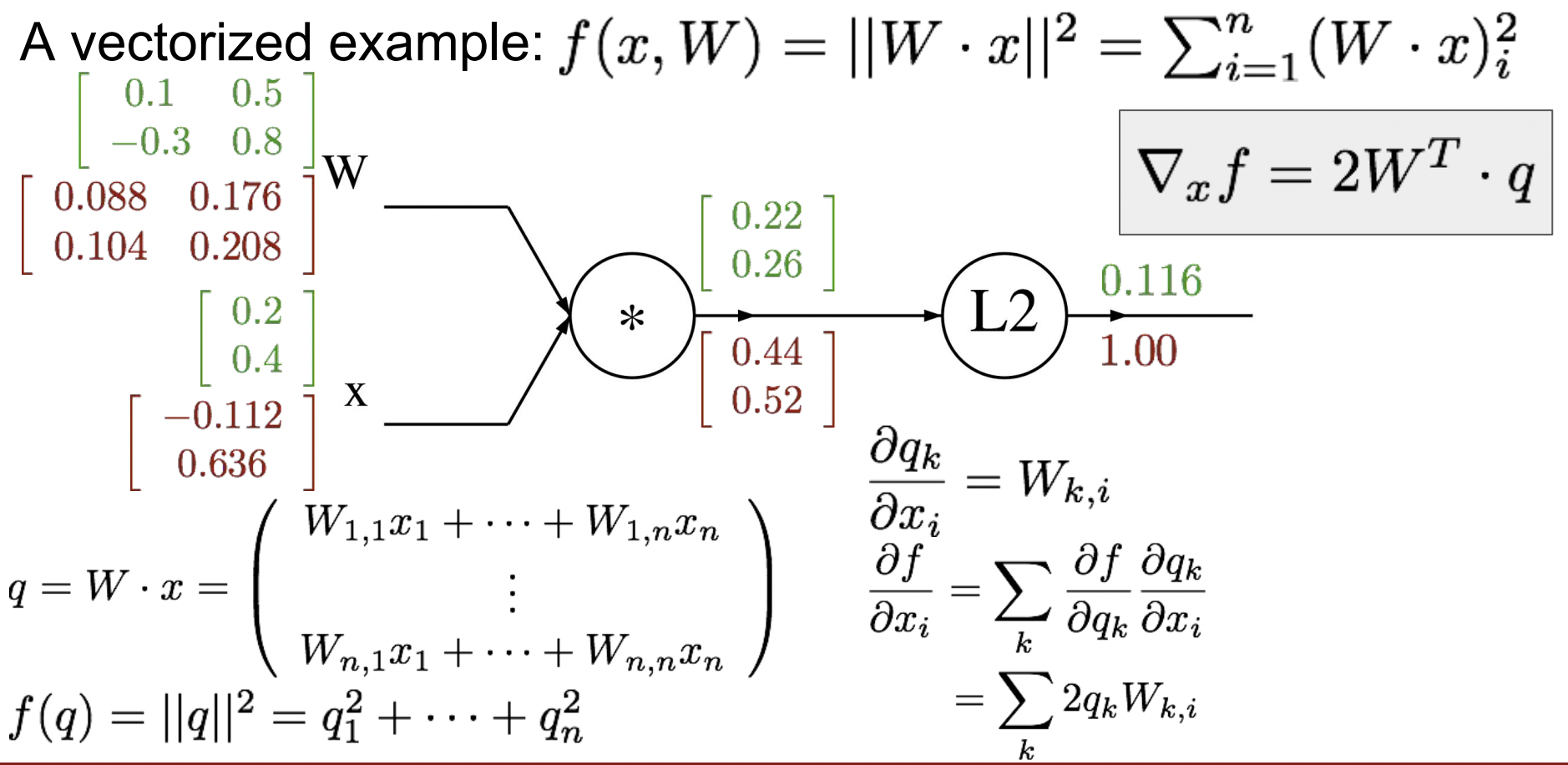
지금까지 우리가 각 노드를 local하게 보고 upstream gradient와 chain rule을 이용해 local gradient를 계산한 것을 forward / backward API로 생각볼 수 있다. Forward pass에서는 각 노드 출력을 계산하는 함수를 구현하고, Backward pass는 chain rule을 이용해 gradient를 계산한다.

Neural Networks
single transformation 대신에 이제는 간단하게 2층 짜리 신경망을 사용해보자.
기본적으로 광범위하게 말하면 신경망은 복잡한 ‘비선형 함수’를 만들기 위해서 간단한 함수들을 계층적으로 여러개 쌓아올린 함수들의 집합(class)이다. (비선형 함수로 만드는 것은 매우 중요한데 왜인지는 나중에 살펴보자) 아래 예제를 보면 첫 번째로 선형 층을 가지고 있고 두 번째로 비선형 층을 가지고 있다. 그리고 마지막으로 socre함수를 얻을 수 있다.

우리는 더 많은 layer를 쌓아 임의의 깊은 신경망을 구성할 수 있다. 즉, 복잡한 네트워크의 경우 이러한 계층을 여러개 쌓는다. -> “Deep neural network”
Where did this idea com from? Neurons!
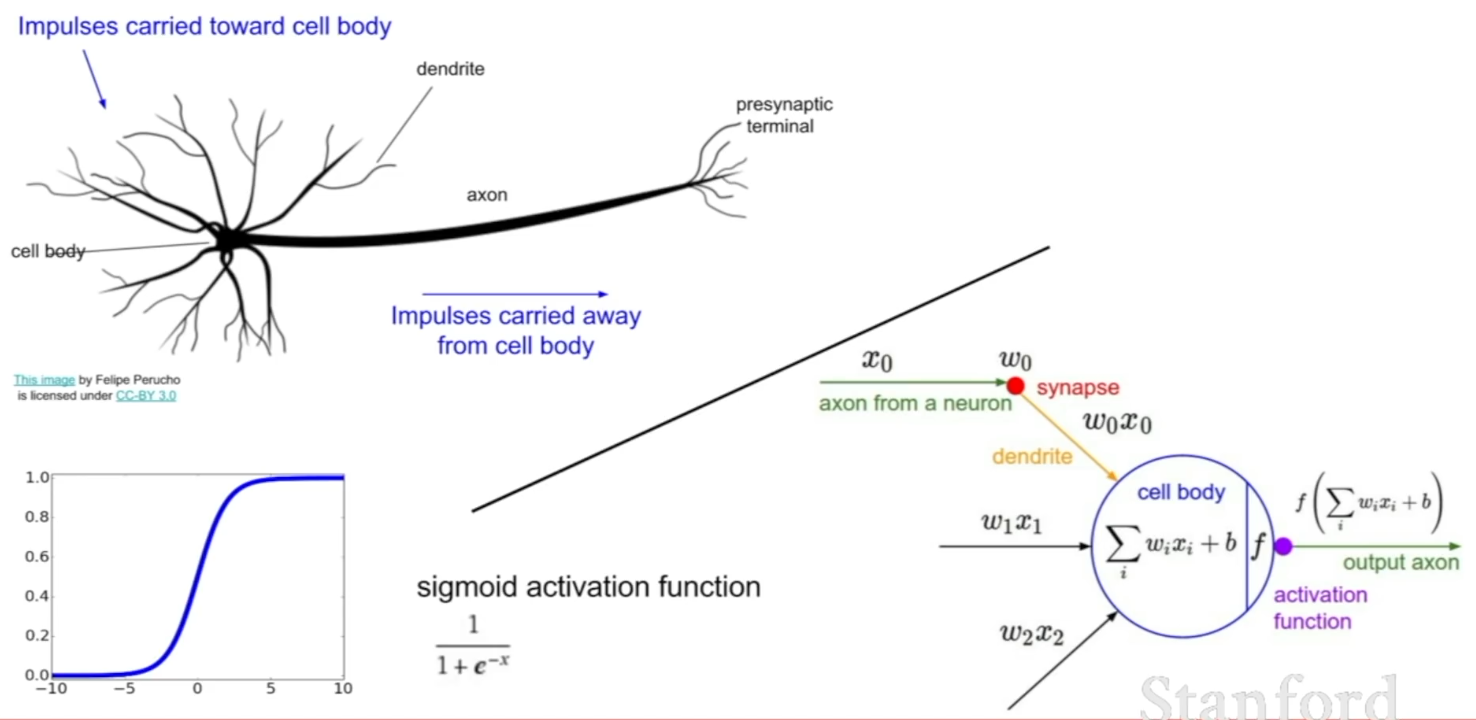
남은 강의에서 다양한 activation function들과 다른 종류의 신경망에 대해서도 계속해서 이야기 할 것이다.