Lecture 5 Convolutional Neural Networks

이번 시간에는 Convolutional Neural Network에 대해 살펴 볼 것이다. 기존 Neural Network와 같은 아이디어이긴 하지만 이번에는 ‘spatial structure(공간적 구조)’를 유지하는 Convolutional Layer에 대해 배울 것이다.

History

1957년 Frank Rosenblatt는 ‘Perceptron’ 알고리즘을 구현한 최초의 기계 Mark I Perceptron을 만들었다. Perceptron은 우리가 앞에서 배운 Wx + b 와 유사한 함수를 사용하는데 출력이 1 또는 0이고, backprop과 유사하게 가중치 W를 update 하는 update rule이 있다.

1960년에는 Widrow와 Hoff가 최초로 Multilayer Perceptron Network인 Adeline and Madaline을 개발했다. 하지만 Backprop과 같은 것들은 없었다.

최초의 Backbprop은 1986년에 Rumelhart가 제안했고 여기에서는 Update rule, Chain rule 등을 볼 수 있다. 이 떄 최초로 network를 학습시키는 것에 관한 개념이 정립되기 시작했다.

하지만 이 이후로 NN을 더 크게 만들지 못하고 새로운 이론이 나오지 못하는 등 머신러닝은 침체되는 듯 했다. 2000년대가 되어서 다시 활기를 찾았는데 2006년 Hinton 와 Salakhutdinov가 논문에서 Deep Neural Network의 학습가능성과 실제로 효과적이라는 것을 보여주었다. 하지만 이것은 현재 알려진 NN은 아니다.

실제로 NN의 광풍이 불기 시작한 것은 2012년이다. Hinton lab에서 나온 논문에서 NN이 음성인식에 좋은 성능을 내었다. 또한 2012년에 Hinton lab의 Alex Krizhevsky이 영상인식에 관한 아주 획기적인 논문이 하나 나온다. 이 논문은 ImageNet Classification에서 최초로 CNN을 사용해 error를 극적으로 감소시키며 놀라운 결과를 도출했다. 이 이후로 ConvNet은 아주 널리 쓰이고 있다.

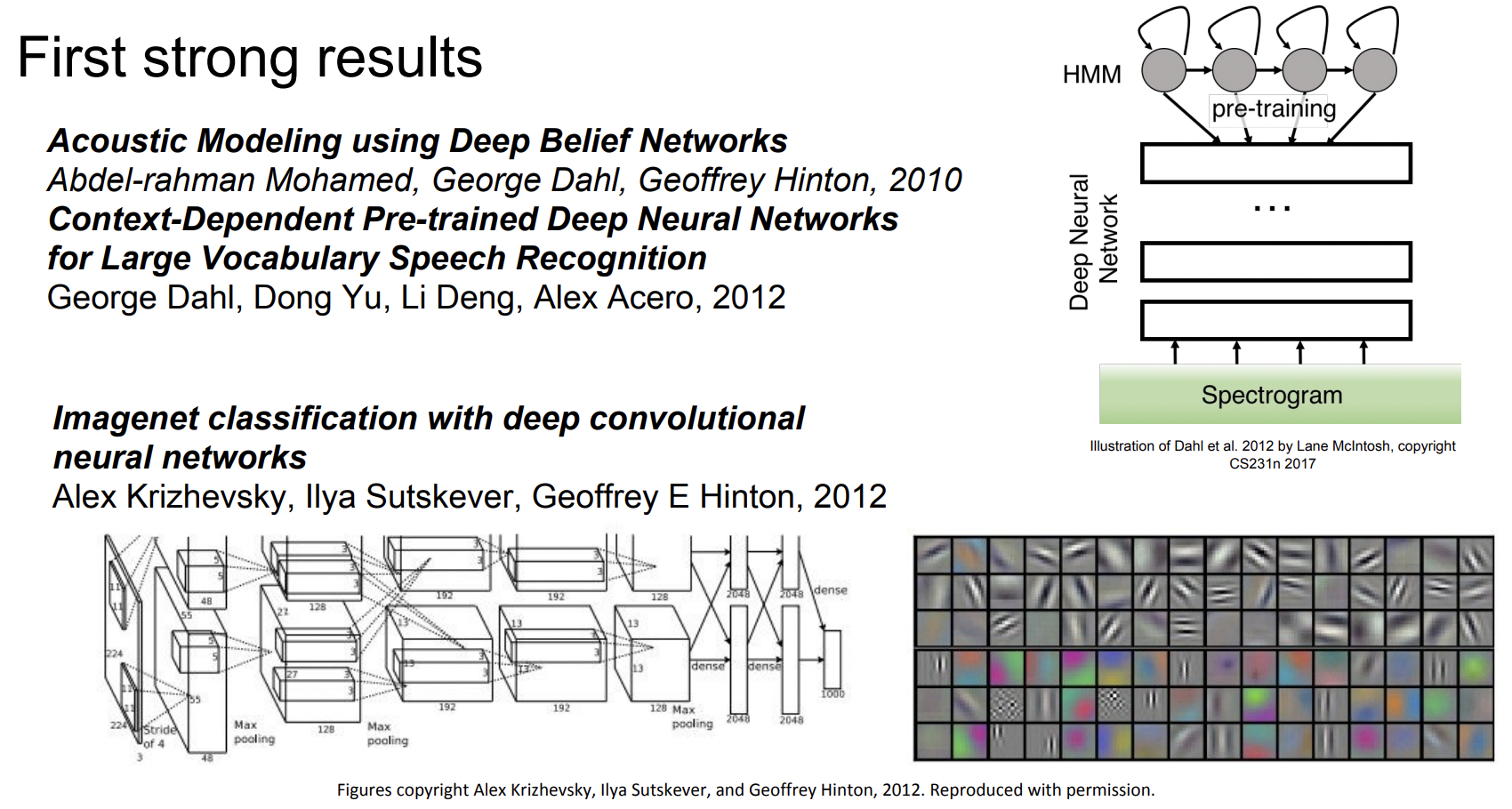
다시 돌아가서 구체적으로 “CNN이 어떻게 유명해졌는지”에 대해 한 번 알아보자.

1998년 LeCun이 최초로 NN을 학습시키기 위해 Backprob과 gradient-based learning을 적용했고 이 방법은 문서인식에 좋은 성능을 냈다. (우편번호 인식) 하지만 아직 이 Network를 더 크게 만들 수는 없었고 데이터(숫자)가 너무 단순했다.

2012년 Alex Krizhevsky가 CNN의 유행을 이르켰고 이 네트워크는 AlexNet이라고 불린다.  LeCun보다 커지고 좀 더 깊어졌다. 하지만 가장 중요한 점은 이제 ImageNet dataset과 같이 대규모의 데이터를 활용할 수 있고, GPU의 성능이 높아졌다는 것이다.

오늘날에 보면 ConvNet은 모~든 곳에 쓰인다. Classification, Retrieval, Detection, Segmentation, 자율주행 자동차 등 많은 곳에서 좋은 성능을 내고 있다.

Convolutional Neural Networks

이제 어떻게 CNN이 동작하는지 살펴보자.

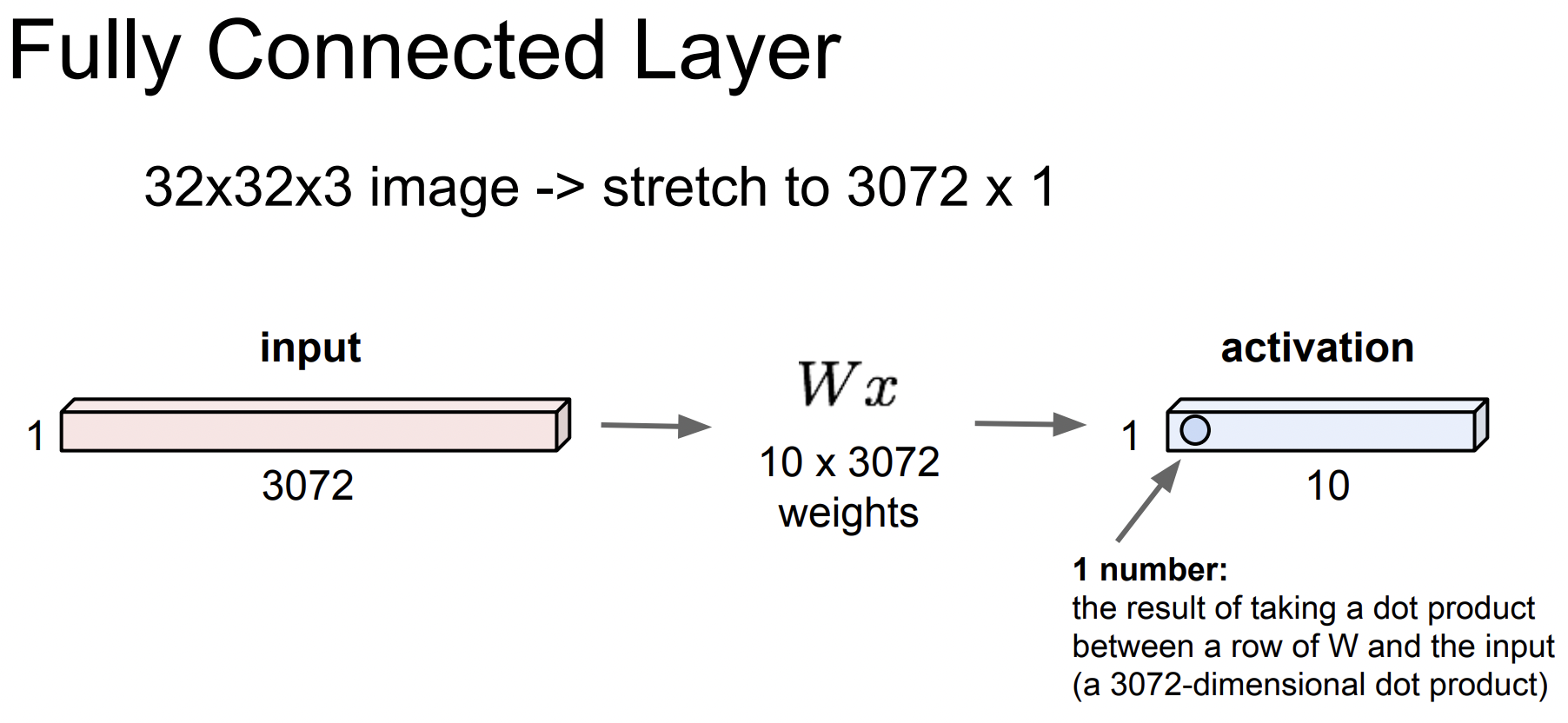
Fully Connected Layer

FC에서 하는 일은 어떤 벡터를 가지고 연산을 한다. 입력으로 32 $\times$ 32 $\times$ 3 이미지가 있으면 이걸 길게 펴서 3072차원의 벡터로 만들고 가중치 $W$ 와 곱한다.($Wx$) 그리고 이 layer의 출력인 activation을 얻는다.(내적한 결과) 아래에서는 10개의 결과값이 있다.

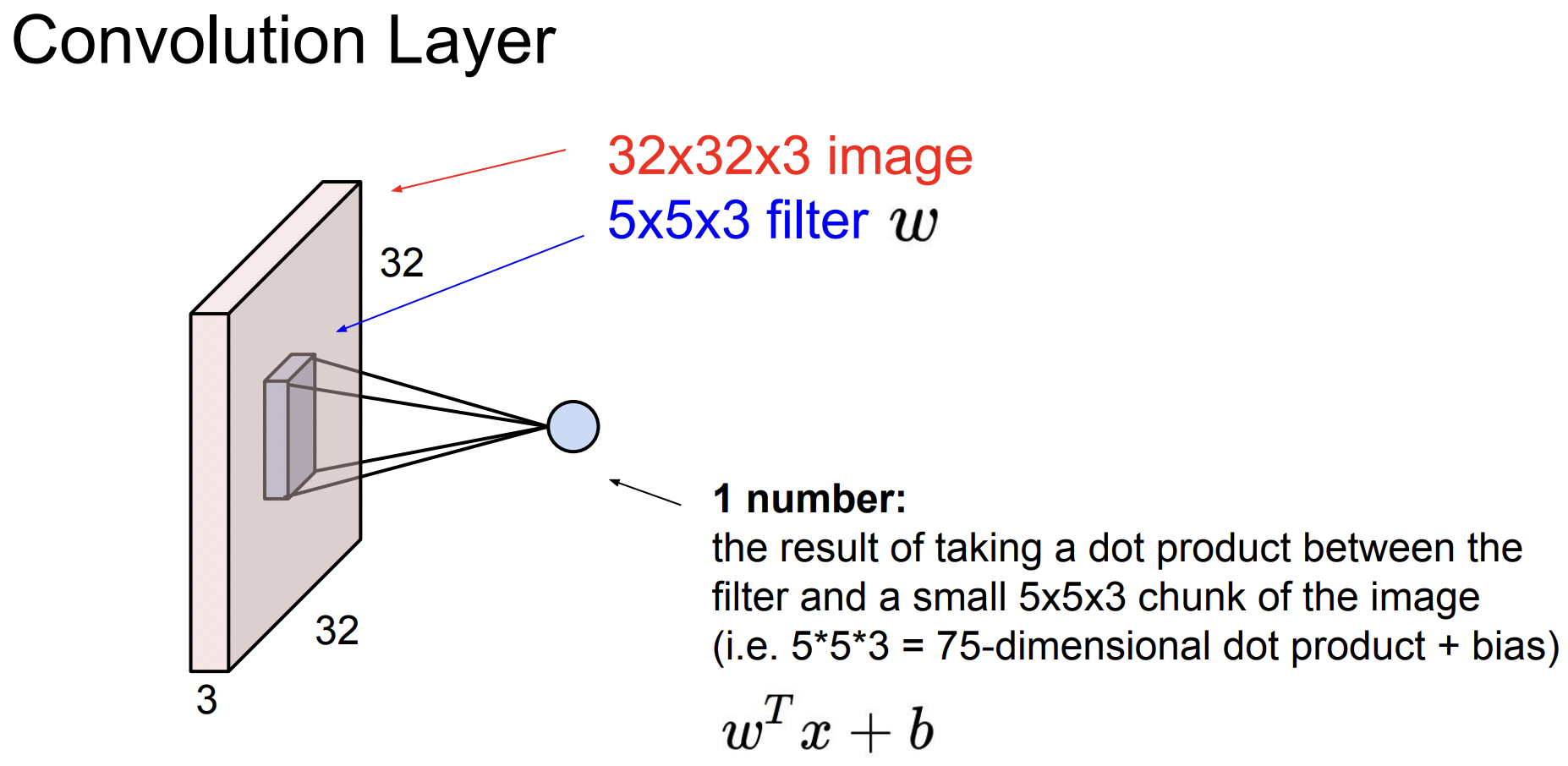
Convolutional Layer와 FC Layer의 주된 차이점은 Convolutional Layer는 기존의 구조를 보존한다는 것이다. FC Layer는 32 \times$32\times$3 이미지를 길게 폈지만 Convolutional Layer은 이미지 구조를 그대로 유지한다.

filter가 우리가 가진 가중치이고(아래에서는 5\times$5\times$3) 이것을 가지고 이미지를 슬라이딩하면서 공간적으로 내적을 수행한다. filter는 입력의 깊이(depth)만큼 확장되며 이것을 가지고 전체 이미지에 내적을 시킨다.

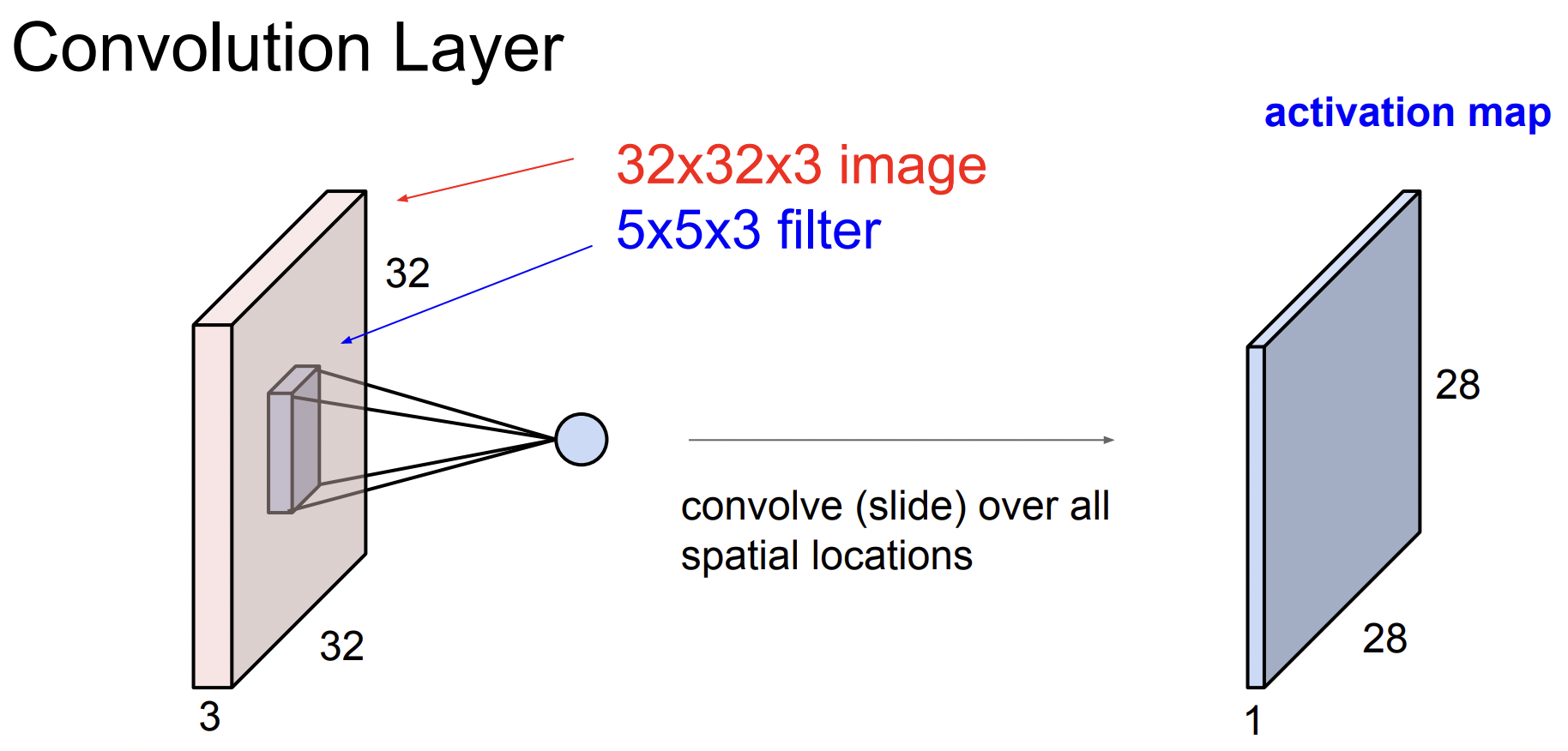
How do we slide?

Convolution은 이미지의 좌상단부터 시작하며 필터의 중앙 값들을 모은다. 필터의 모든 요소를 가지고 내적을 수행하면 하나의 값을 얻게되고 이 값을 다시 Output activation map의 해당 위치에 저장한다.

(입력과 activation map의 차원이 다를 수 있다 → 출력행렬의 크기는 슬라이드를 어떻게 하느냐에 따라 달라짐)

하나의 필터를 가지고 전체 이미지에 Convolution 연산을 수행하면 activation map 이라는 출력값을 얻게 된다. 보통 Convolution Layer 에서는 필터 마다 다른 특징을 얻고 싶어하기 때문에 여러개의 필터를 사용한다. 아래처럼 6개의 5$\times$5 필터가 있으면 총 6개의 activation map 을 얻는다.

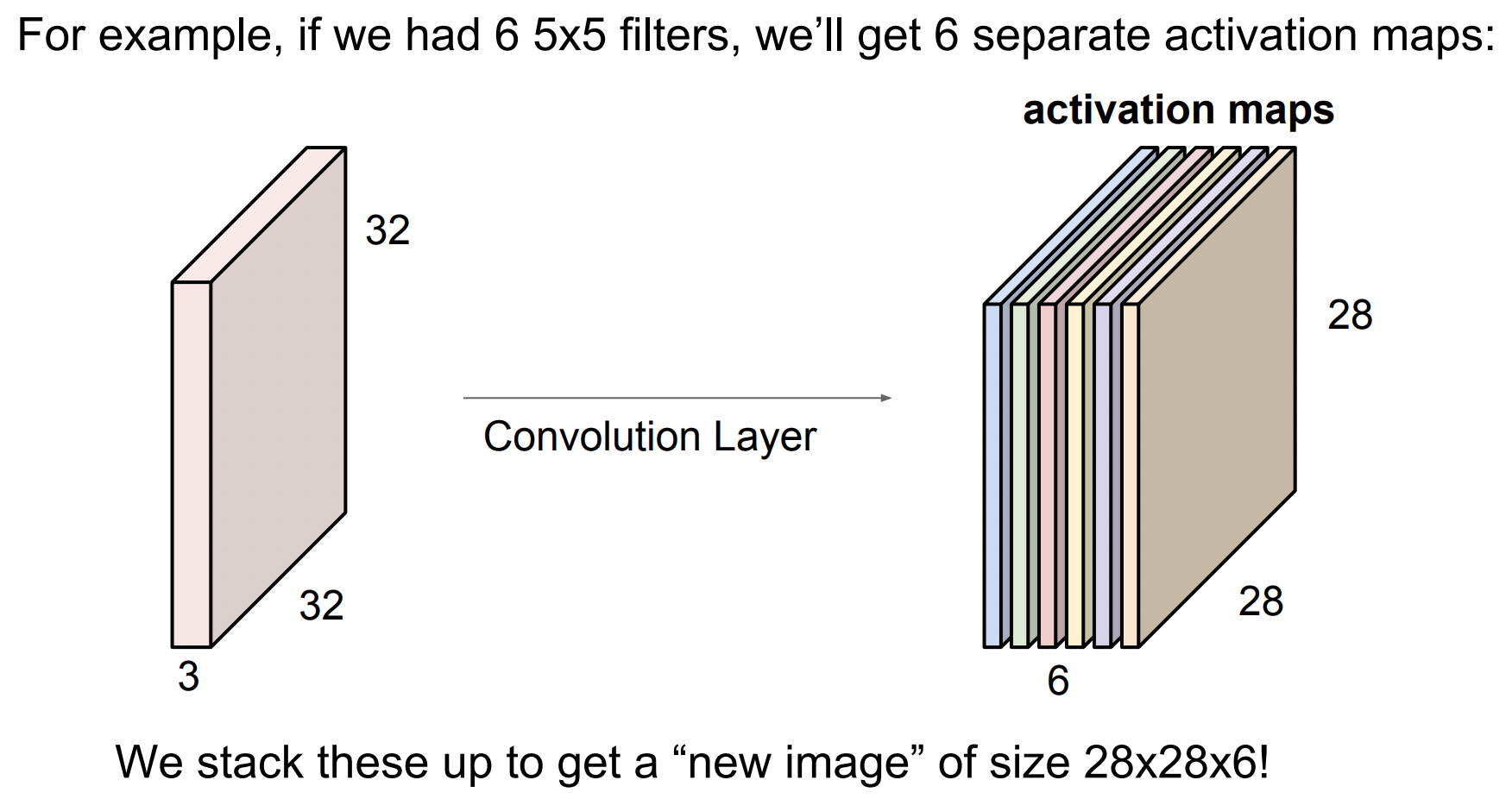
ConvNet 은 아래와 같이 Conv Layer들의 연속된 형태가 될것이다. 그리고 각각을 쌓아 올리게 되면 간단한 Linear Layer로 된 Neural Network가 된다. 이제 그 사이 사이에 activation function을 넣을 것이다. (Ex. ReLU) 그러면 이제 Conv, ReLU의 반복이 되고 각 Layer의 출력은 다음 Layer의 입력이 되는 구조가 된다.

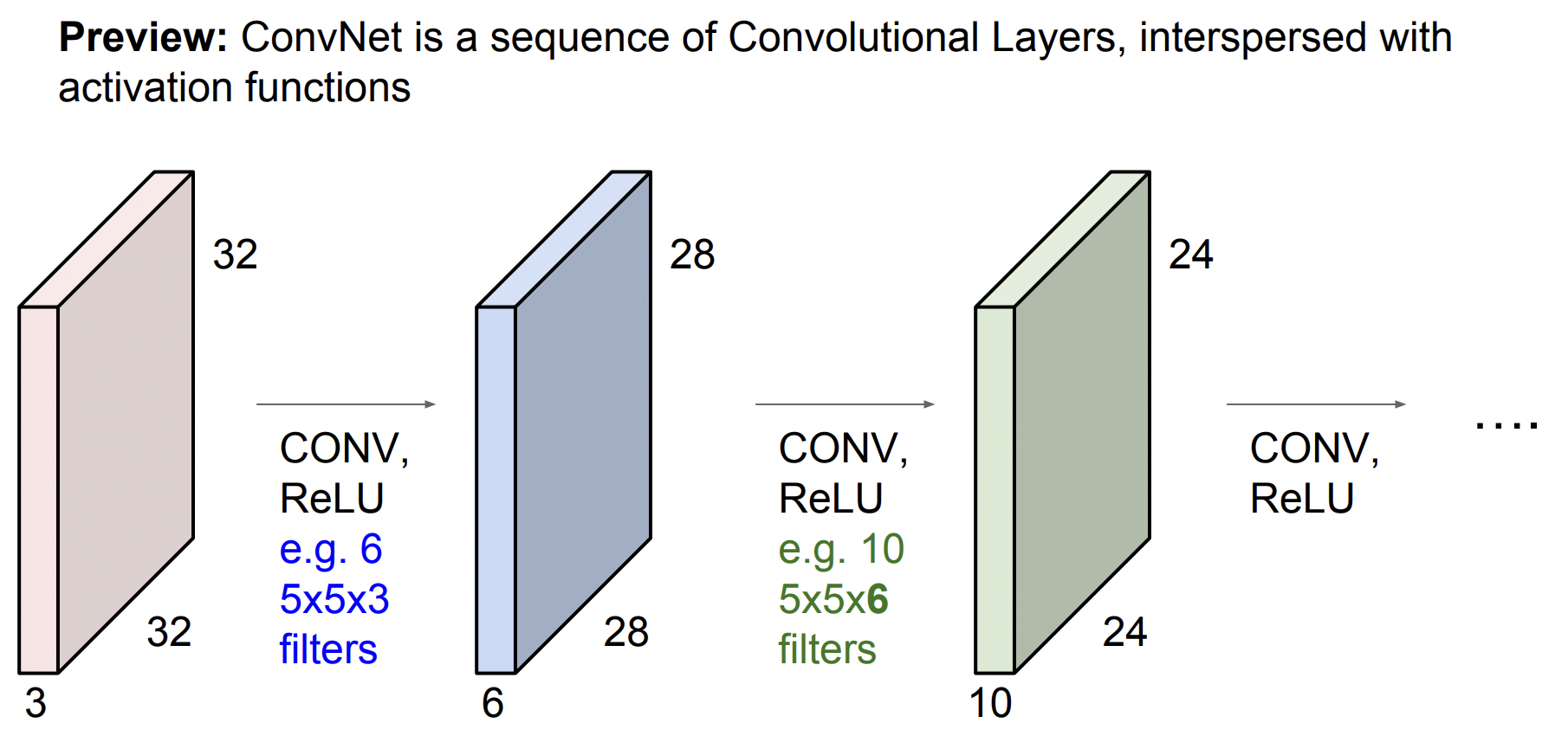
여러개의 Layer를 쌓고나면 결국 각 필터들이 계층적으로 학습하는 것을 볼 수 있다.

• 앞쪽에 있는 필터들은 edge와 같은 low-level feature를 학습한다.
• Mid- level은 corner나 blobs등과 같이 좀 더 복잡한 특징을 가진다.
• 그리고 high-level features를 보면 좀 더 객체와 닮은 것들이 출력으로 나온다.

포인트는 Layer의 계층에 따라 단순 → 복잡한 특징들이 각각에 존재하고 있다는 것이다.

Activation map

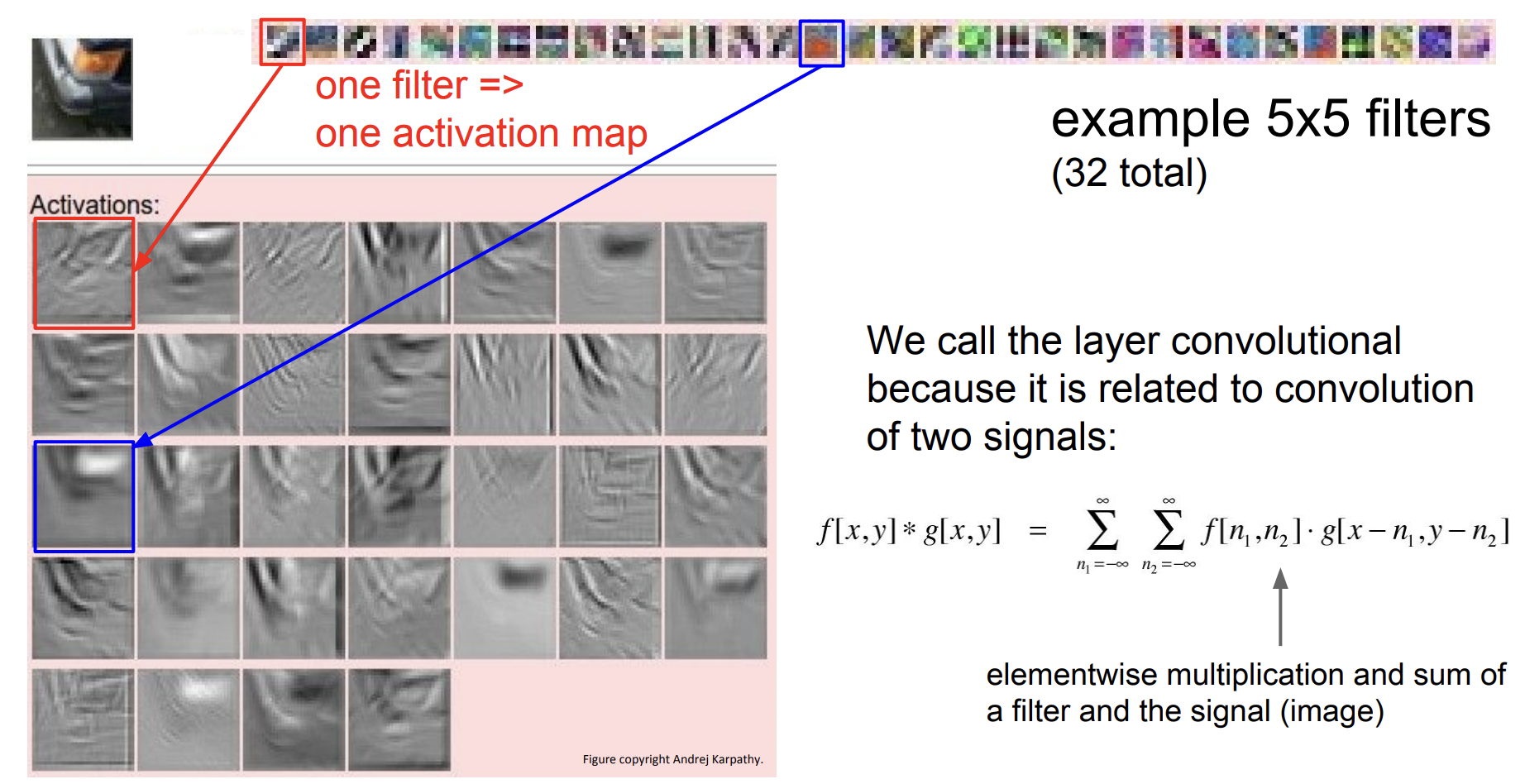
아래는 각 필터의 출력값인 Activation map이다. 입력 이미지는 자동차의 한 부분 코너로 오른쪽 상단에는 5$\times$5 필터들을 시각화한 것이고, 분홍색 부분은 이미지와 필터간 Convolution의 activation 결과이다. 빨간 박스 filter의 activation 결과를 보면 edge 를 찾고 있는 듯 하고 이 필터를 슬라이딩 시키면 이 필터와 비슷한 부분의 값들은 값이 더 커진다. 즉, 각 *activation은 이미지가 필터를 통과한 결과가 되며 이미지 중 어느 위치에서 이 필터가 크게 반응하는지를 보여준다.*

Spatial dimension

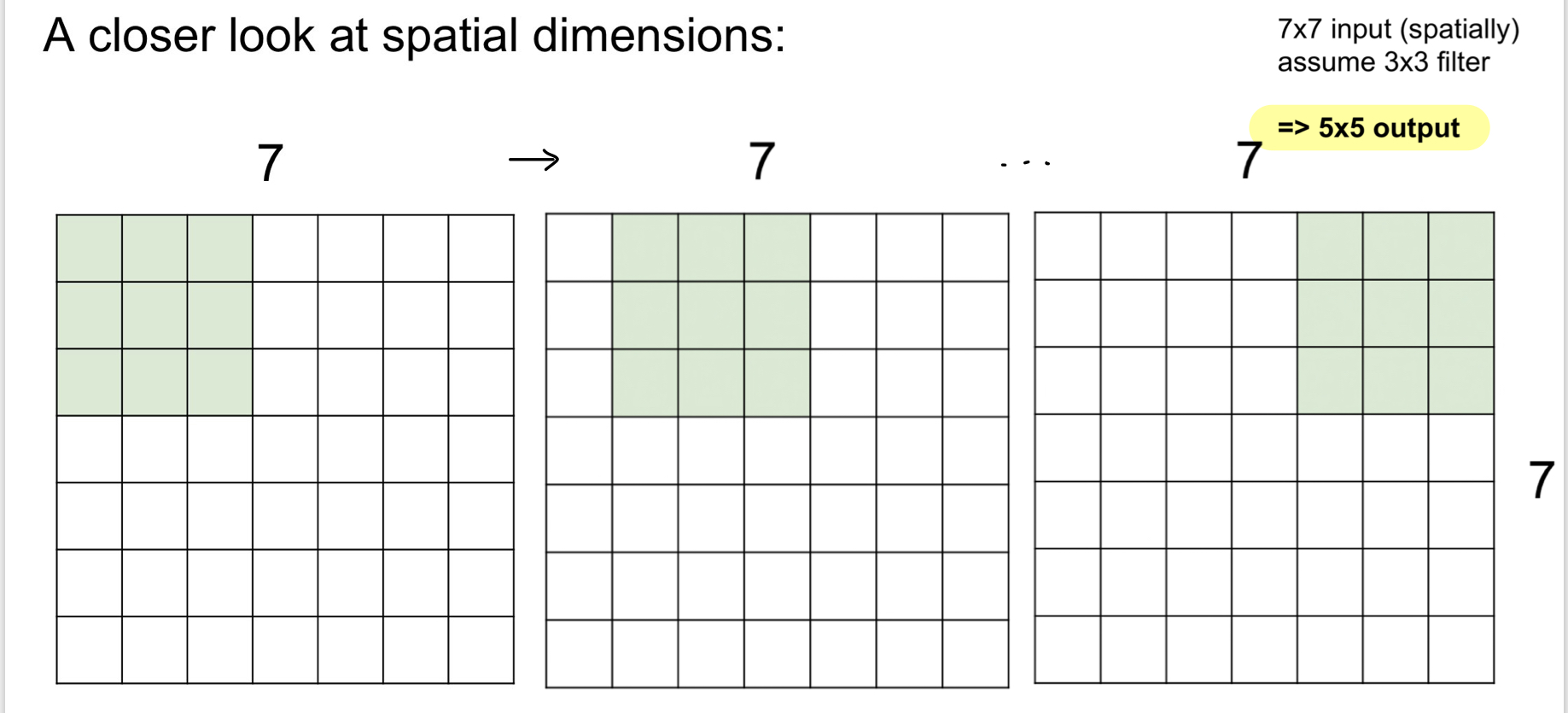
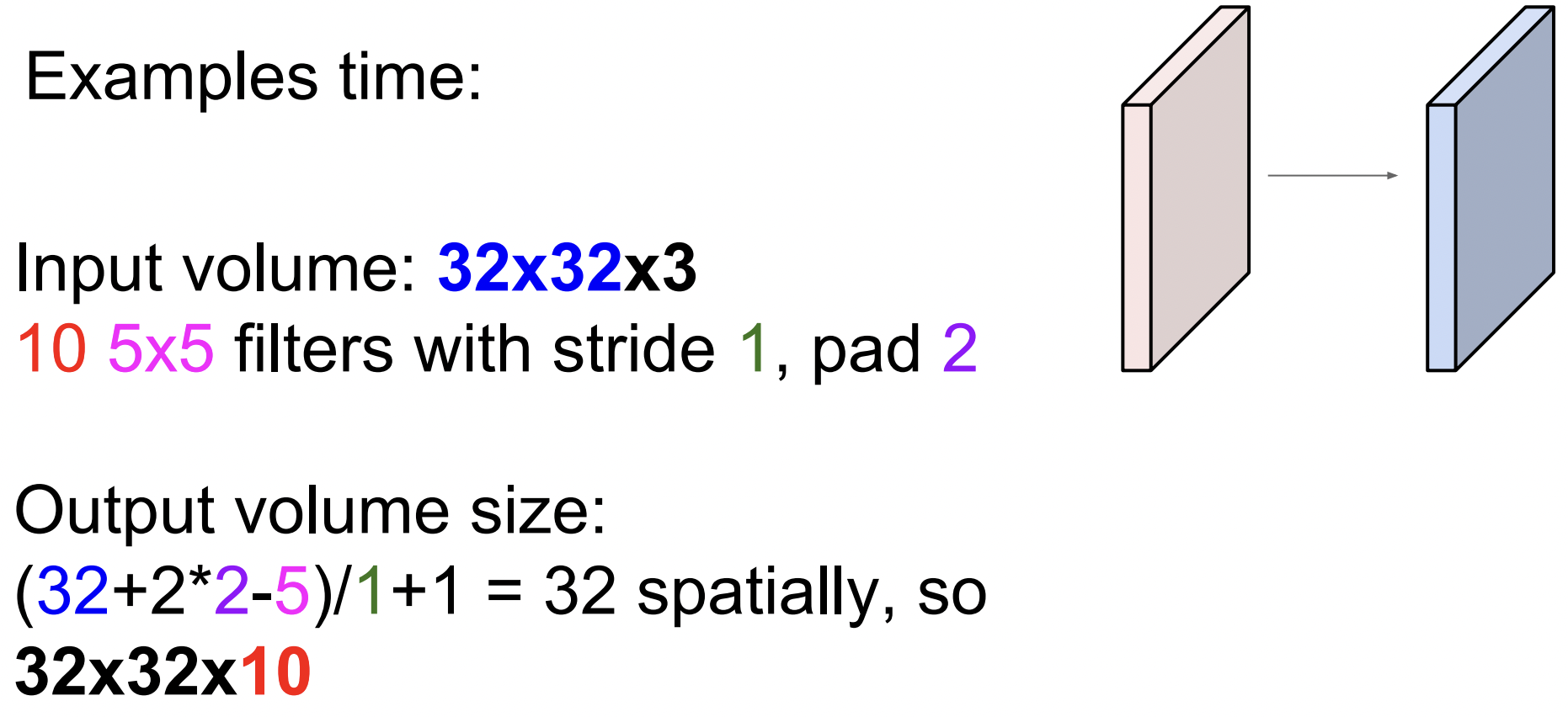
앞에서 봤던 예제에서 32\times$32\times$3 image에서 5$\times$5$\times$3 filter로 슬라이딩 해서 어떻게 28$\times$28 activation map이 생기는 지를 알아보자.

간단한 예로 7\times$7 입력에 3\times$3 필터를 생각해보자. 왼쪽 상단부터 시작해 해당 값 들의 내적을 수행하면 나온 값들을 activation map의 좌 상단에 위치하게 된다. 다음으로 필터를 오른쪽으로 1칸 움직이면 또 다른 값을 얻을 수 있다. 이렇게 계속 반복하게 되면 5$\times$5 출력을 얻을 수 있다. (좌우, 상하 5번씩만 수행 가능하기 때문)

이제 한칸 슬라이딩이 아닌 두칸으로 해보자. 이때 움직이는 칸을 바로 “stride”라고 한다. stride 가 2일때는 출력은 3$\times$3 이 된다. stride 가 3이면 어떨까? 이미지에 딱 맞아 떨어지지 않는다. 이러면 결과가 불균형해지기 때문에 사용해서는 안된다. 그래서 상황에 따라 출력 사이즈를 구할 수 있는 수식이 있다.

출력 사이즈를 의도한대로 만들어주기 위해 가장 흔히 쓰는 기법은 zero-pad이다. 이미지 가장자리에 0을 채워넣어 코너 부분에서도 필터 연산을 수행할 수 있다. zero-padding후에 7\times$7입력에 3\times$3필터연산을 수행하면 출력은 어떻게 될까? 7$\times$7출력을 얻게 된다.

이렇게 Padding을 하면 출력 사이즈를 유지시켜주고(만약 padding이 없으면 출력 사이즈는 아주 빠르게 줄어들고 깊은 네트워크에서는 activation map은 엄청 작아지게 돼서 일부 정보를 잃게 된다) 필터의 중앙이 닿지 않는 곳도 연산을 가능하게 해준다.

Example

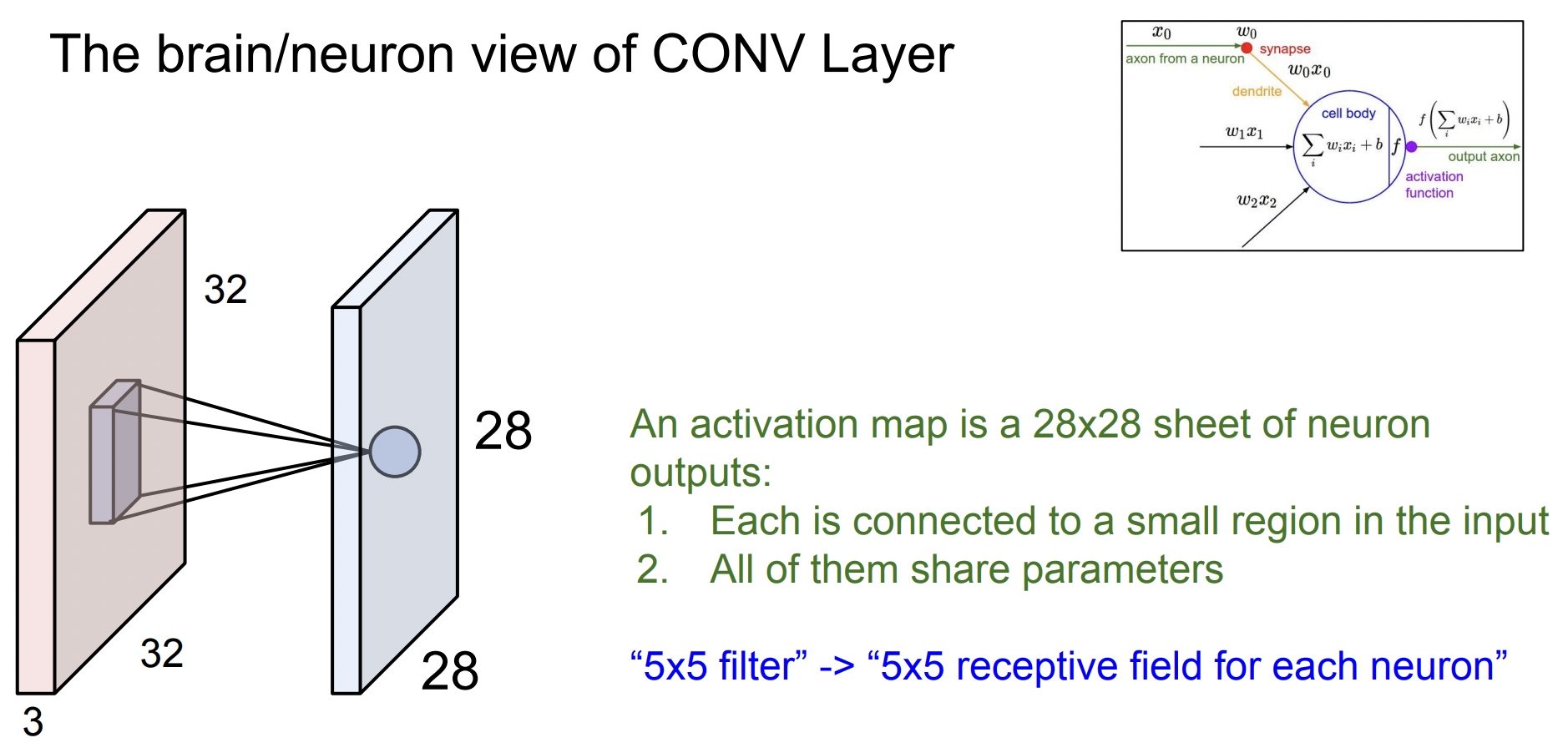
Conv Layer에서는 이미지의 특정 위치에서 필터를 가지고 내적을 수행해 하나의 값을 얻는다. 이것은 아래 그림 오른쪽의 내적과 같은 아이디어로 입력이 들어오면 $W$를 곱하고($W$는 필터 값) 하나의 값을 출력한다. 하지만 가장 큰 차이점은 뉴런 아이디어는 Conv Layer처럼 슬라이딩을 하는 것이 아닌 특정 부분에만 연결되어 Local connectivity를 가지고 있다는 것이다. 그래서 하나의 뉴런은 한 부분만 처리하고 그런 뉴런들이 모여서 전체 이미지를 처리하는 것이다. 이런 식으로 spatial structure을 유지해 activation map을 만드는 것이다.

• Receptive field : 한 뉴런이 한번에 수용할 수 있는 input field
  

Pooling Layer

Pooling Layer는 Representation들을 더 작고 관리하게 쉽게 해주기 위해 Downsampling을 해준다. (왜 Representation을 작게 만드는지? -> 파라미터의 수가 줄고 공간적인 invaiance 가능성)

예를 들어 224\times$224\times$64 인 입력이 있다면 이것을 112$\times$112$\times$64로 “spatially(공간적)”으로 줄여주고, Depth는 아무것도 하지 않는다. (Only pooling Spatially!)

일반적으로 Max Pooling이 많이 쓰인다. Pooling도 얼마만큼의 영역을 한번에 묶을지 필터 크기를 정할 수 있다. 아래 그림은 2$\times$2 필터에 stride는 2로 슬라이딩 하면서 연산을 한다. 대신 내적을 하는 것이 아닌 필터 안에서 가장 큰 값 중에 하나를 고른다. 아래를 보면 빨간 부분에서 6이 가장 크고, 초록 부분에서는 8이 가장 크다. 그리고 보통 Pooling시에는 겹치지 않는 것이 일반적이다. 요즘에는 downsample을 위해 pooling보다는 stride를 많이들 사용하는데 pooling도 stride 기법이라고 할 수 있다.

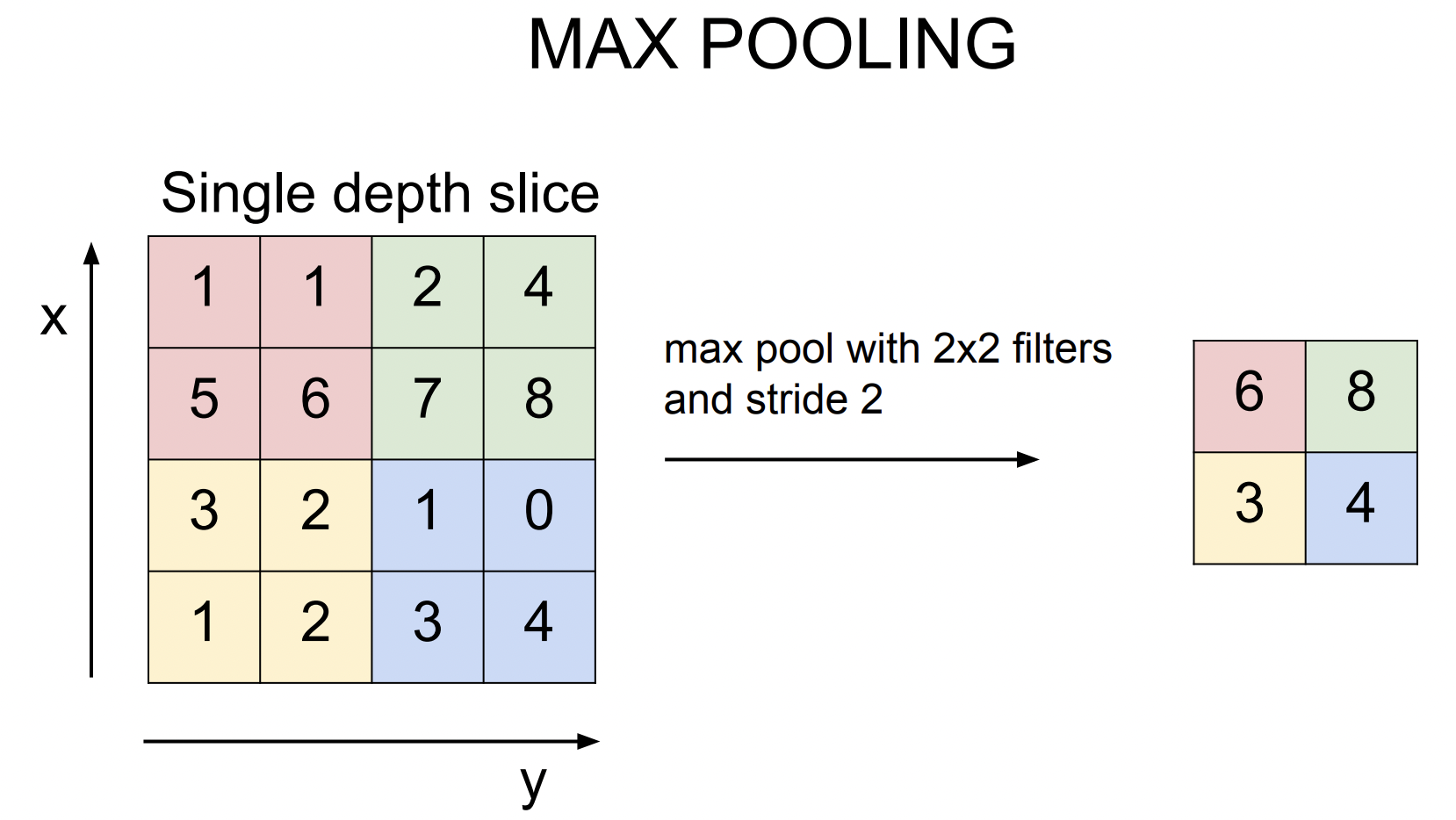
Pooling layer에서는 보통 padding을 하지 않는데 왜냐면 우리는 downsampling을 하고 싶고 Conv처럼 코너의 값을 계산하지 못하는 경우도 없기 때문이다. 그래서 Pooling할 때는 padding을 고려하지 않아도 되고 그냥 downsample만 하면 된다. 가장 널리 쓰이는 필터 사이즈는 2\times$2, 3\times$3이고, 보통 stride는 2로 한다.

CNN 마지막에는 FC Layer가 있다. 여기 마지막 Conv Layer의 출력은 3차원 volume(w$\times$h$\times$d)으로 이뤄진다. 이 값들을 모두 stretch해서 1차원 벡터로 만들고 이를 가지고 FC Layer의 입력으로 사용한다. 그럼 이제 ConvNet의 모든 출력을 서로 연결할 수 있게 되는 것이다. 여기에서는 공간적 구조(spatial structure)를 신경쓰지 않고 최종적인 추론으로 score를 출력으로 나오게 한다.(아래에서 각각의 열은 출력의 Activation Map이다.)