Lecture 6 Training Neural Networks, Part I

Eunjin Kim·2022년 7월 20일

목록 보기

6/6

Activation Functions

선형적인 층만 여러개 쌓는 것은 선형성에 의해서 하나의 층으로 합칠 수 있으므로 의미가 없다. 그래서 더 복잡한 non-linear 함수를 만들기 위해 선형층 중간에 activation function을 넣어주면서 계층적인 구조의 비선형함수 네트워크로 만들어 준다.

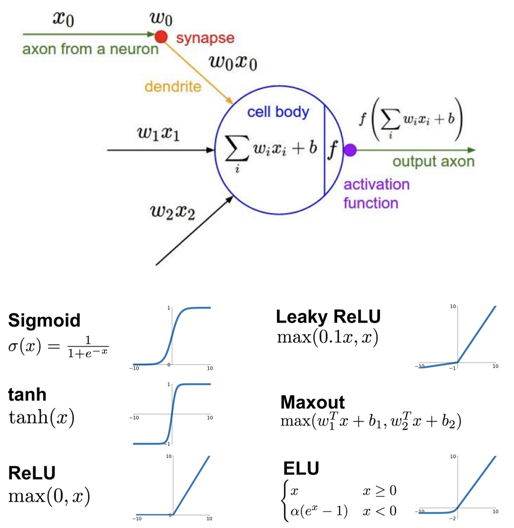
1. Sigmoid

오래전부터 쓰였으며 입력이 $[0, 1]$ 사이의 값이 되도록 해준다. (입력의 값이 크면 1에 작으면 0에 가까움)

💢 하지만 Sigmoid에는 3가지 문제점이 있다.

⓵ Saturated neurons “kill” the gradients

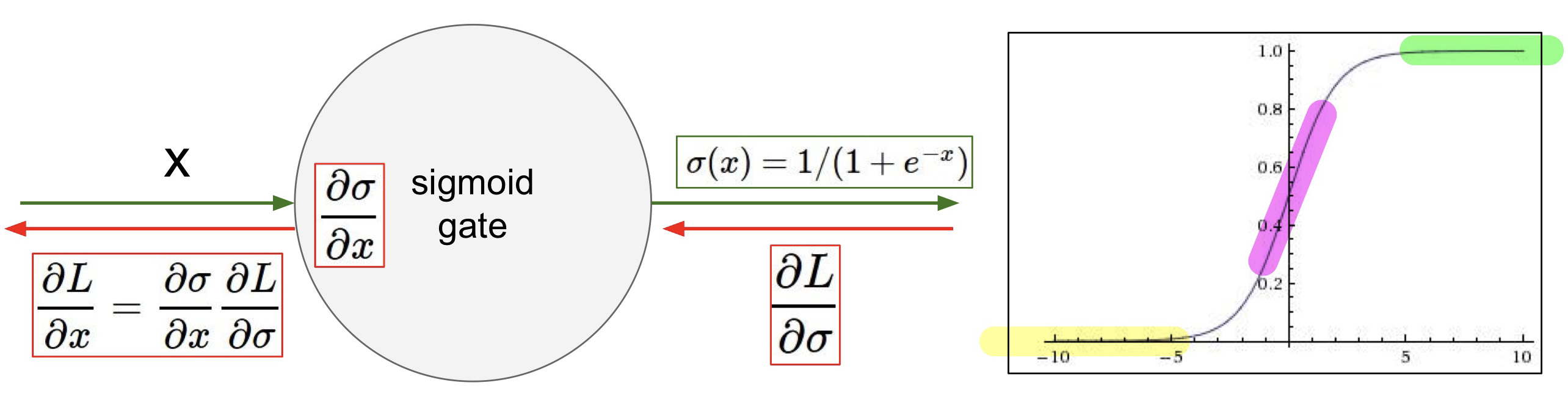
What happens when x = -10? gradient = 0 (노란색 부분)
What happens when x = 0? works well (분홍색 부분)
What happens when x = 10? gradient = 0 (연두색 부분)

sigmoid 함수에서 입력의 총합이 크거나 작으면 gradient가 0이 되어버려서 이 값이 아래로 내려가면서 거의 0에 가까운 값이 backprob된다. 그래서 gradient가 계속 죽게되는 Vanishing Gradient 문제가 생긴다.

⓶ Sigmoid outputs are not zero-centered

Sigmoid의 입력( $x$ )이 항상 양수이면 어떨까?

$x$ 가 어떤 $W$ 와 곱해져서 활성함수를 통과하면 $W$ 에 대한 local gradient는 그냥 $X$ 가 된다. 그래서 local gradient는 ‘전부 양수’ or ‘전부 음수’가 된다.

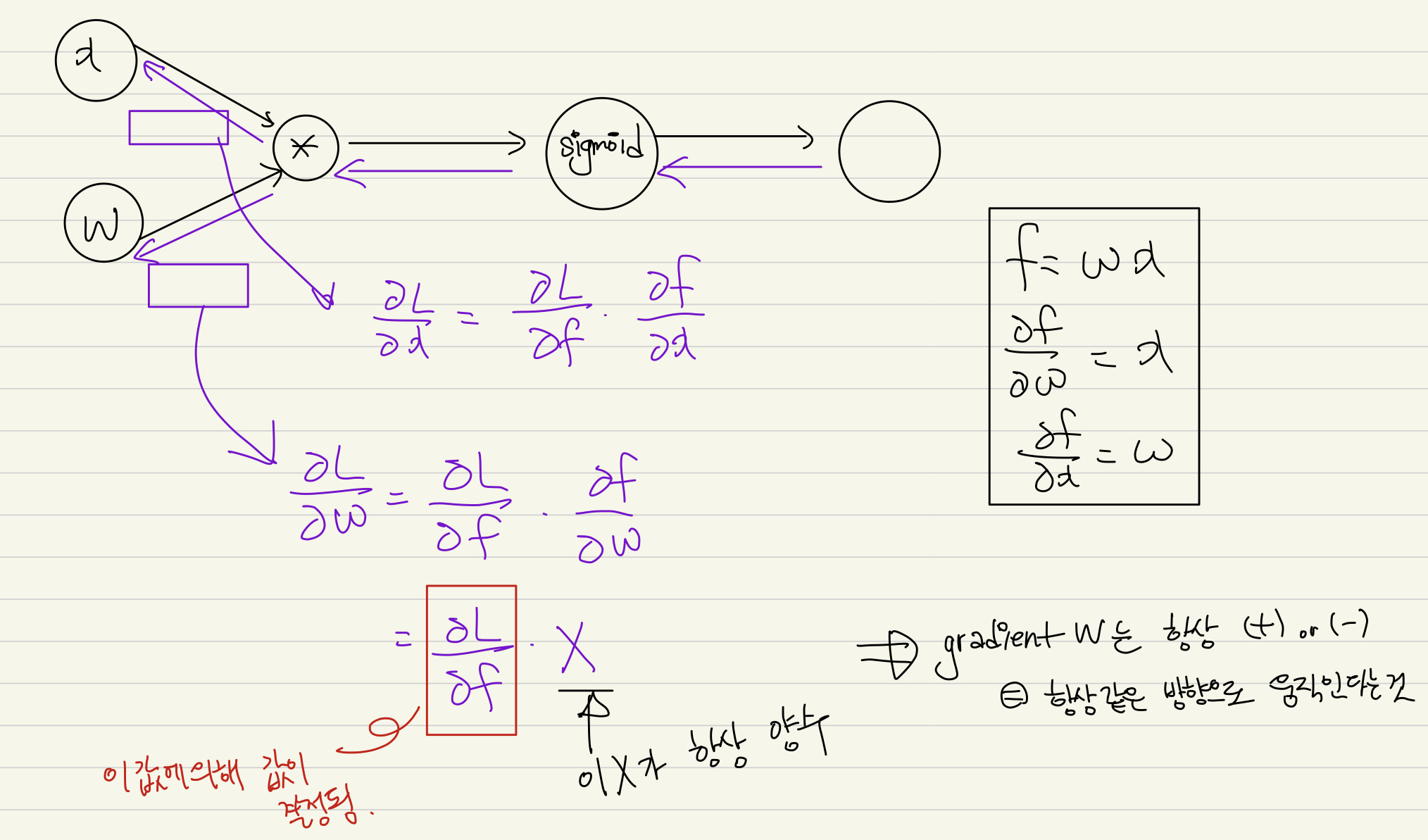
결론적으로 gradient의 부호는 그저 위에서 내려온 gradient의 부호와 같기 때문에 $W$ 가 모두 같은 방향으로 움직일 것이다. 즉, 파라미터를 업데이트할 때 다같이 증가하거나 다 같이 감소하거나 할 수 밖에 없다.

→ very inefficient 😢

아래를 보면 $W$ 가 두개의 축으로 이루어져 있는 2차원 예제가 있다. 전부 양수 또는 음수로 업데이트 된다는 것은 gradient가 이동할 수 있는 방향이 4분면 중 아래의 두 영역 뿐이라는 것이고 이 두 방향으로만 gradient가 업데이트된다.

빨간 화살표의 처음 부분이 초기 시작점이라고 해보자. 하지만 가장 최적의 $W$ 업데이트(파란색 화살표) 방향으로는 움직일 수 없기 때문에 여러번 gradient 업데이트를 수행해줘야 한다.

(빨간 화살표 방향같이, gradient가 이동 가능한 방향으로만 이동할 수 있게 된다.)

$∴$ 입력 $x$ 가 양수, 음수를 모두 가지고 있으면 전부 같은 방향으로 움직이는 일은 발생하지 않을 것이기에 우리는 일반적으로 zero-mean data를 원한다.

⓷ exp() is a bit compute expensive : minor problem

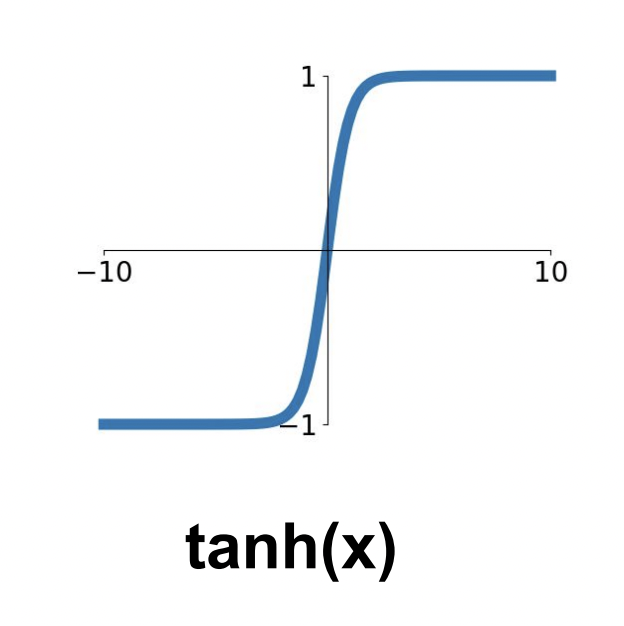
2. Tanh

sigmoid와 유사하게 생겼는데 범위가 $[-1, 1]$ 이다.

zero-centered 여서 2번째 문제는 해결되지만 1번째 문제는 여전히 남아있다. (gradient 가 flat한 부분이 있다)

3. ReLU

element-wise 연산을 수행하며 입력이 음수면 0, 양수면 입력 값 그대로 출력된다.( $f(x) = max(0, x)$ ) ReLU의 양수 부분은 saturate 되지 않고 max 연산이기 때문에 빠르게 계산할 수 있다. (생물학적으로도 sigmoid보다 타당성이 높음.)

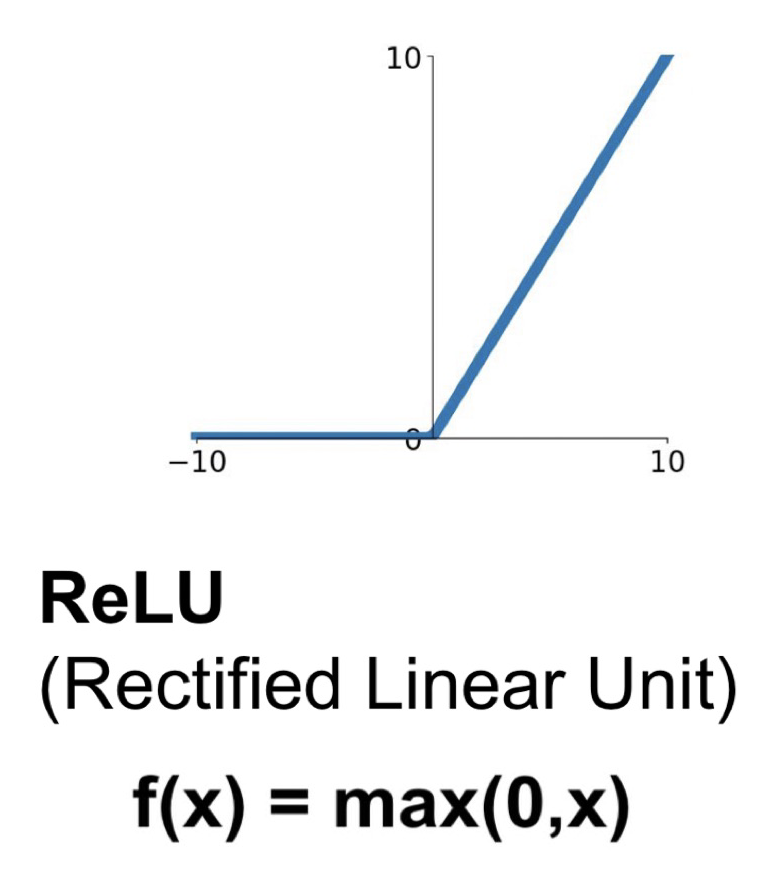
but❗️ ReLU의 문제점은 zero-centered가 아니라는 것과 음수의 경우에는 saturation 된다는 것이다.

What happens when x = -10? gradient = 0
What happens when x = 0? gradient = 0
What happens when x = 10? works well (linear region)

→ 기본적으로 ReLU는 gradient의 절반을 KILL🗡 (dead ReLU)

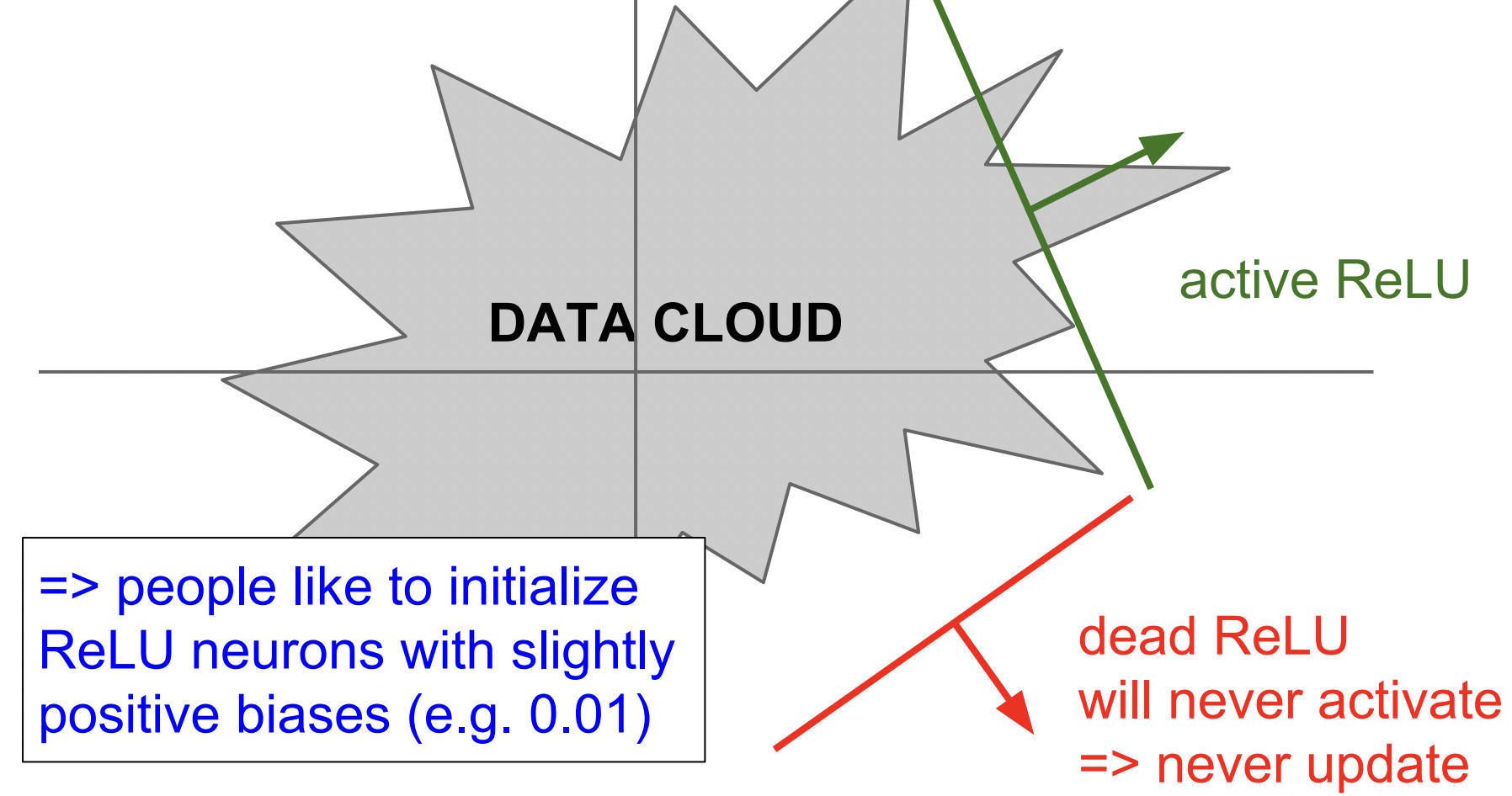
아래에서 볼 수 있듯이 ReLU가 data cloud(=training data)에서 떨어져 있으면 dead ReLU가 발생할 수 있다. dead ReLU에서는 어떤 데이터 입력도 activate 되지 않고 update되지 않는다.

반면에 active ReLU는 일부는 activate, 일부는 non-activate 이다. WHY? 👀

초기화를 잘못한 경우
- 가중치 평면이 데이터로 부터 멀리 떨어져 있어서 activate 되는 경우가 없고 backprop 이 일어나지 않는다.
learning rate가 지나치게 높은 경우
- update 를 지나치게 크게 해서 가중치가 날뛰면서 ReLU가 데이터의 manifold 를 벗어난다. → 처음에는 학습 잘 되다가 갑자기 die.

그래서 실제로는 update시에 active ReLU가 될 가능성을 조금이라도 높이기 위해 positive biases를 추가해 초기화해주기도 하는데 대부분은 zero-bias를 이용한다.

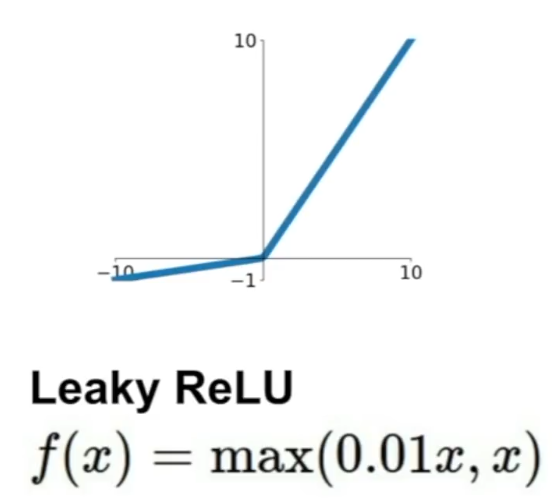
4. Leaky ReLU

ReLU에서 조금 수정되어 음의 부분에서 0이 아닌 약간의 기울기를 줘서 saturation 문제를 해결할 수 있다. 또한 계산도 효율적이고 Dead ReLU 현상도 없다.

5. PReLU(parametric rectifier)

음의 부분에서 기울기가 있다는 점에서 Leaky ReLU와 유사하지만 다만 여기에서는 기울기가 $\alpha$ 라는 파라미터로 결정된다. 활성 함수가 좀 더 유연하도록 고정 값이 아닌 backprop으로 학습시키는 파라미터로 만들었다.

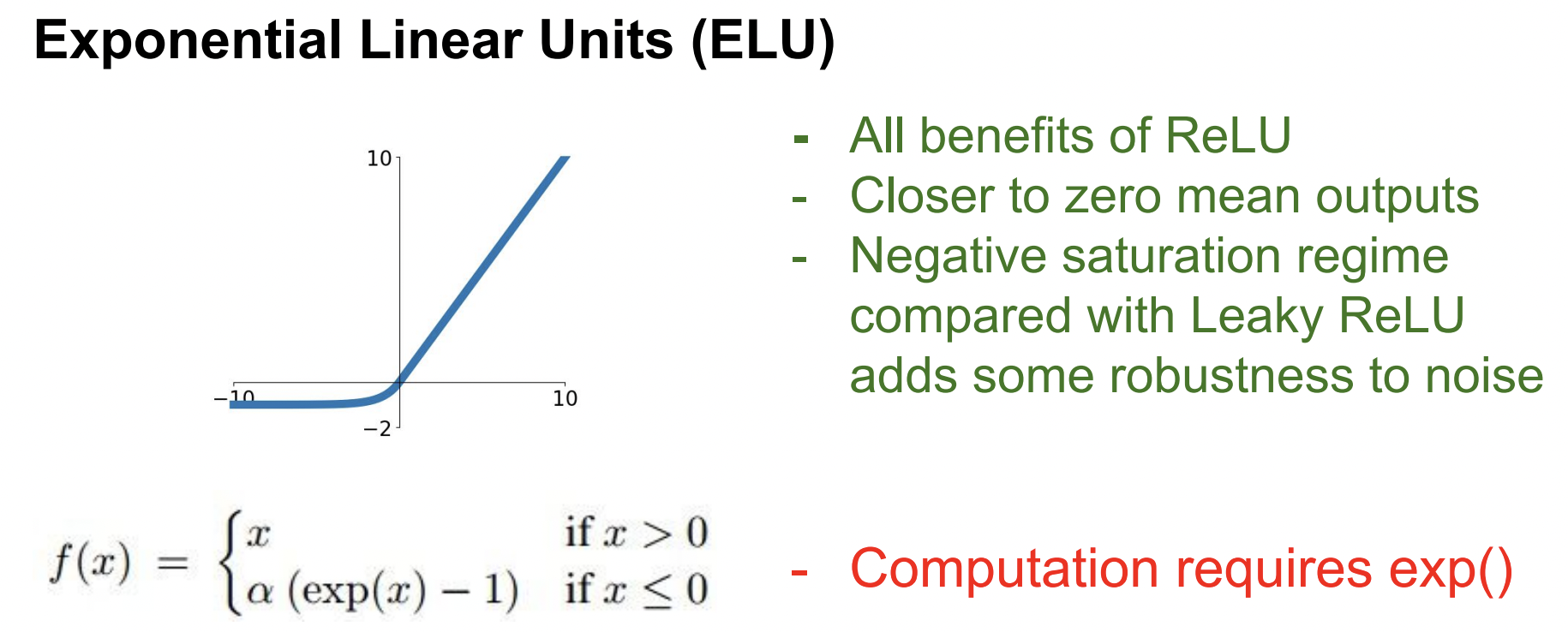
6. ELU(Exponential Linear Units)

ReLU의 이점을 가져오고 ELU에는 음의 부분에서 기울기를 갖지 않고 saturation 되게 한다. ELU는 이런 saturation이 noise에 좀 더 robustness(강하다고) 주장한다.

(ReLU와 Leaky ReLU의 중간 → zero-mean 출력을 내지만 saturation을 가지고 있음)

7. Maxout Neuron

입력을 받아들이는 특정 기본형식을 미리 정의하지 않고 $max(w_1^Tx + b_1, w_2^Tx + b_2)$ 를 사용한다.

Maxout 또한 선형이기 때문에 saturation 되지 않고 gradient가 죽지 않을 것이다. 하지만 문제점은 뉴런당 파라미터의 수가 두배가 된다는 것이다. $(w_1, w_2)$

💡 가장 많이 쓰이는 것은 ReLU이고 사용할 때는 learning rate를 신경써서 결정해줘야 한다. Sigmoid는 가장 구식이고 잘 동작하지 않아서 사용하지 않는 것이 좋다.

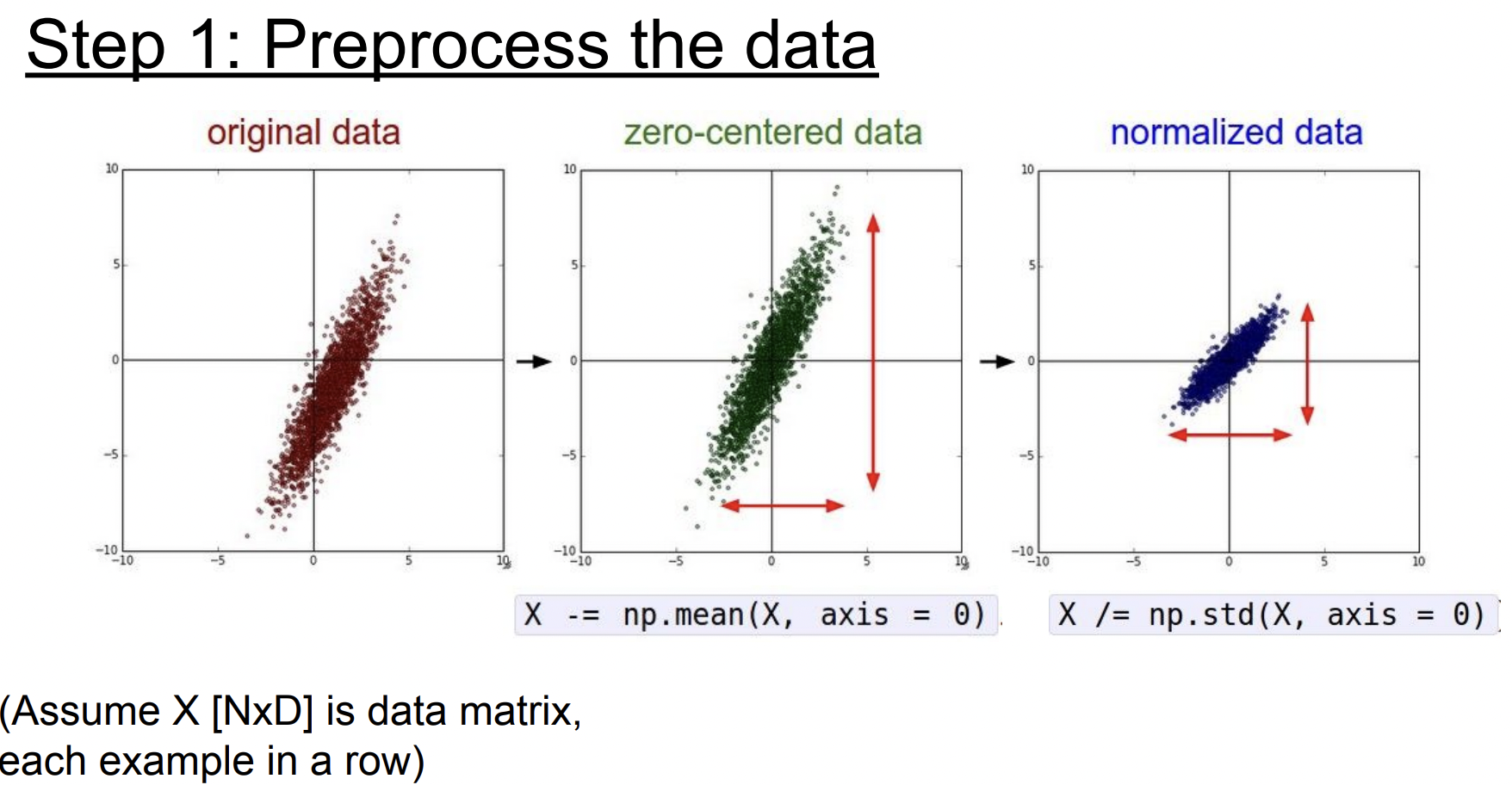
Data Preprocessing

일반적으로 입력 데이터는 전처리를 해준다. (가장 대표적인 전처리 과정은 zero-mean으로 만들고 normalize하는 것)

👀 왜 하쥬??

앞에서 본 문제에서 입력이 전부 양수인 경우에는 모든 뉴런이 양수인 gradient 를 얻게 된다. 이는 최적하지 못한(suboptimal) 최적화가 된다.

normalization을 해주는 이유는 모든 features가 동일한 범위 안에 있게 해서 전부 동등한 contribute 를 할 수 있도록 하기 위해서이다 .

(실제로 이미지의 경우 전처리로 zero-centering 정도만 해주고 정규화는 하지 않는다. 왜나면 이미지는 이미 각 차원 간에 스케일이 어느정도 맞춰져 있기 때문)

Weight Initialization (가중치 초기화)

🌝 어떻게 가중치를 초기화 할까?

2-layer NN 을 생각해보면 처음에 어떤 초기 가중치들이 있고 gradient를 계산해서 가중치를 업데이트 한다.

Q: what happens when $W=0$ init is used?

모든 뉴런이 같은일을 할것이다. 가중치가 0이라면 backprob의 입력이 0이기 때문에 출력이 같고 결국 gradient도 같다. 그래서 모든 가중치가 같은 값으로 업데이트 되어서 뉴런이 모두 똑같이 생기게 된다.

가중치 초기화 방법 ⓵ Small random numbers (임의의 작은 값으로 초기화)

초기 $W$ 를 표준정규분포에서 샘플링 후, 표준편차를 1e-2(=0.01)로 만들어 좀 더 작은 값으로 스케일링 해주는 식으로 모든 가중치를 임의의 작은 값으로 초기화한다.

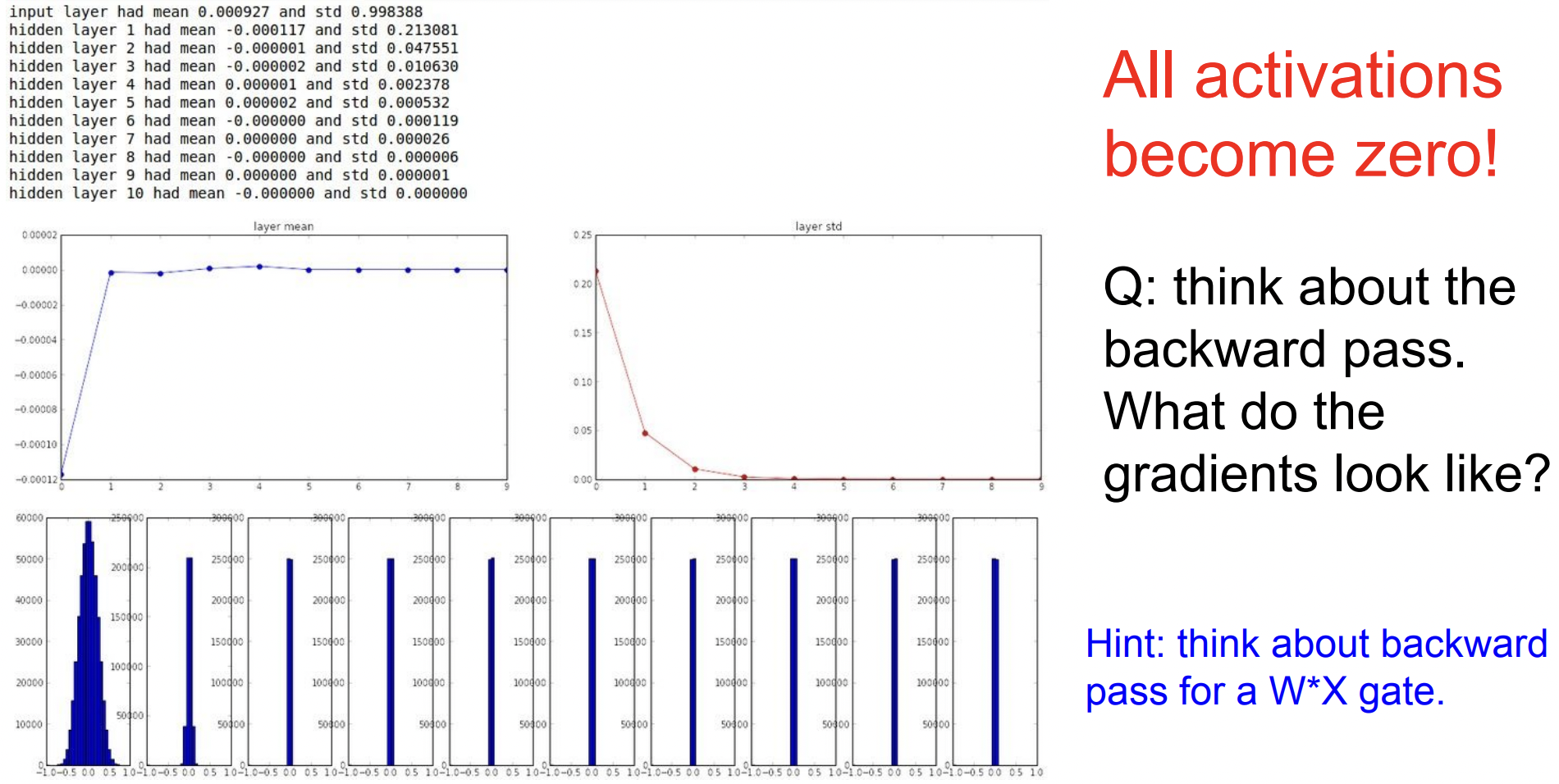
하지만 작은 네트워크에서는 잘 동작하지만 네트워크가 깊어지면 문제가 발생한다. 좀 더 깊은 네트워크를 가지고 아래에서 봐보자.

10- layer network
각 layer마다 500 neurons
활성 함수: tanh
가중치는 임의의 작은 값으로 초기화

데이터를 랜덤으로 만들어서 forward pass 시켜 각 레이어별 activations 수치를 통계화시켜 보면 아래와 같다. (각 레이어 출력의 평균(mean)과 표준편차(std)를 계산)

가운데 부분을 보면 mean은 0에 수렴하는데 활성 함수인 tanh가 zero-centered 이니까 0에 수렴하는 것은 당연히 알 수 있다.

반면 표준편차는 가파르게 줄어들어 0에 수렴한다. 맨 밑 그래프를 보면 첫번째 레이어에서는 표준정규분포 형태로 좋은 분포를 형성하고 있지만 $W$ 를 곱할수록 $W$ 가 너무 작은 값이라서 출력값도 급격히 줄어들어 0에 수렴한다. 결국 모든 활성 함수도 0이 되버린다.

Q. Think about the backward pass. What do the gradients look like?

이제 Backwards pass를 생각해보면 가중치를 업데이트 하기 위해 Upstream gradient에 $W$ 의 gradient인 $X$ 를 곱한다. 여기서 $X$ 도 엄청 작은 값 이기 때문에 결국에는 업데이트가 잘 일어나지 않는다.

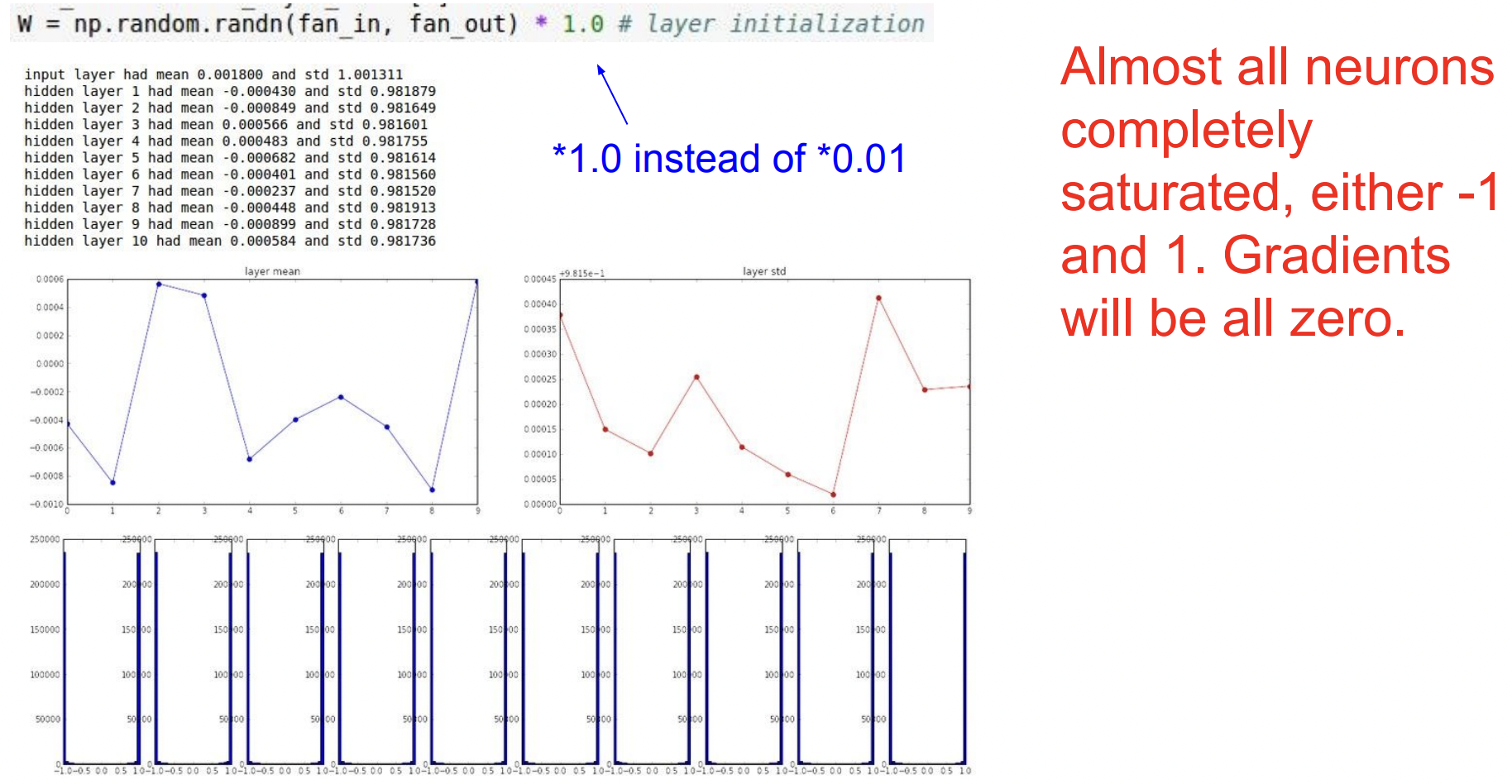
가중치 초기화 방법 ⓶ weight 0.01 -> 1.0 (큰 값으로 가중치 초기화)

tanh 그래프를 생각해보면 가중치가 큰 값이면 출력이 항상 -1 또는 1이 되면서 값들이 saturation 될 것이다. 그래서 gradient는 모두 0이 돼서 가중치 업데이트가 일어나지 않는다.

이처럼 reasonable한 가중치를 정하는 것은 정말 어렵다. → 너무 작으면 vanish 너무 크면 saturate 😢

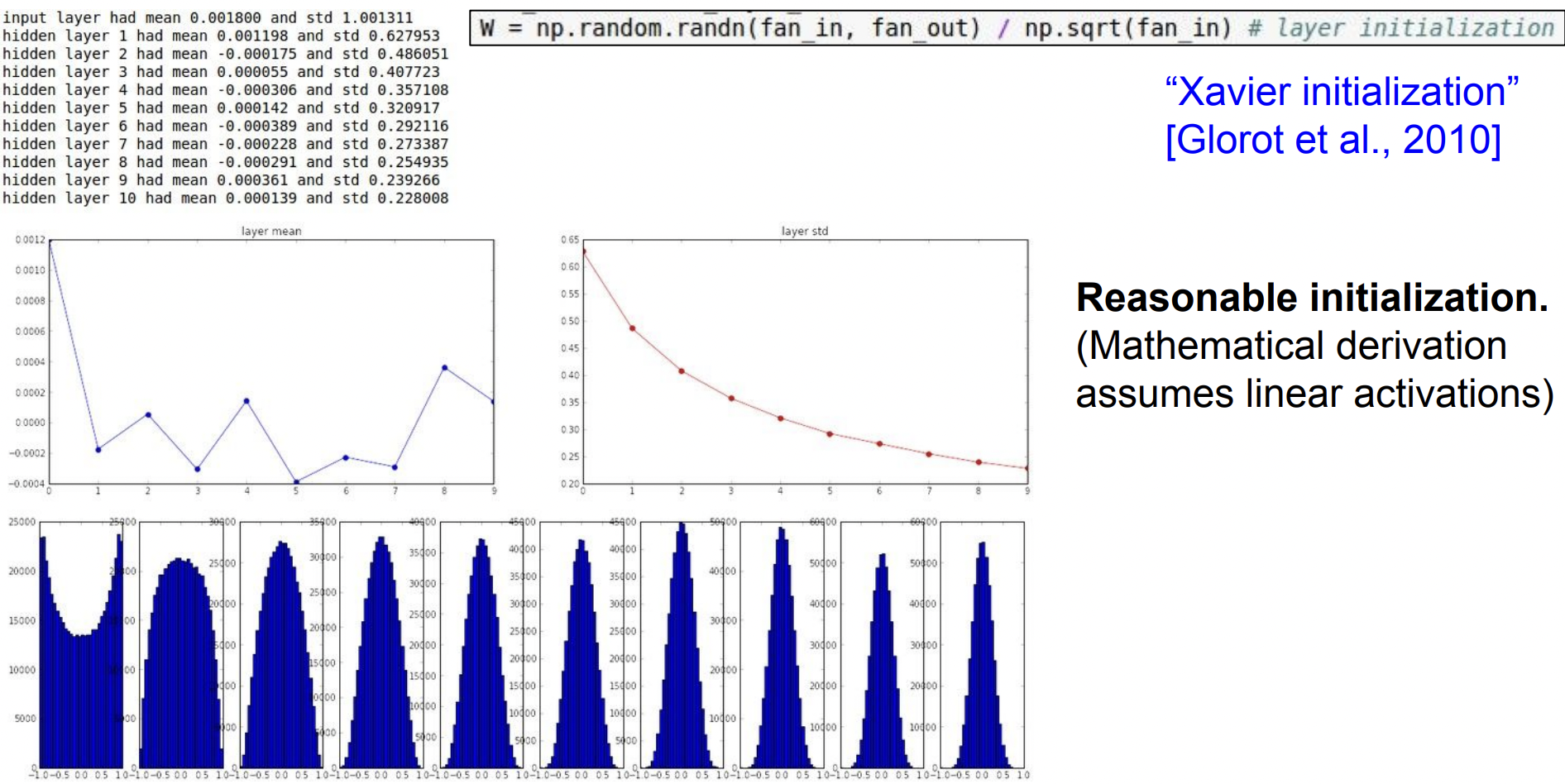
Xavier initialization

좋은 가중치 초기화를 위한 방법 중 널리 알려진 하나는 ‘Xavier initialization’ 이다.

아래 식을 보면 Standard gaussian 으로 뽑은 값을 ‘입력의 개수’로 스케일링 해준다.

W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)

기본적으로 Xavier initialization 가 하는 일은 입/출력의 분산을 맞춰주는 것이다.

입력의 수가 작으면 더 작은 값으로 나누고 좀 더 큰 값을 얻고 더 큰 가중치가 필요한데, 작은 입력의 수가 가중치와 곱해지기 때문에 가중치가 더 커야만 출력의 분산만큼 큰 값을 얻을 수 있다. 반대로 입력의 수가 많은 경우에는 더 작은 가중치가 필요하다.

현재는 Linear activation이 있다고 가정하고 있다.(tanh의 경우 active region안에 있다고 가정)

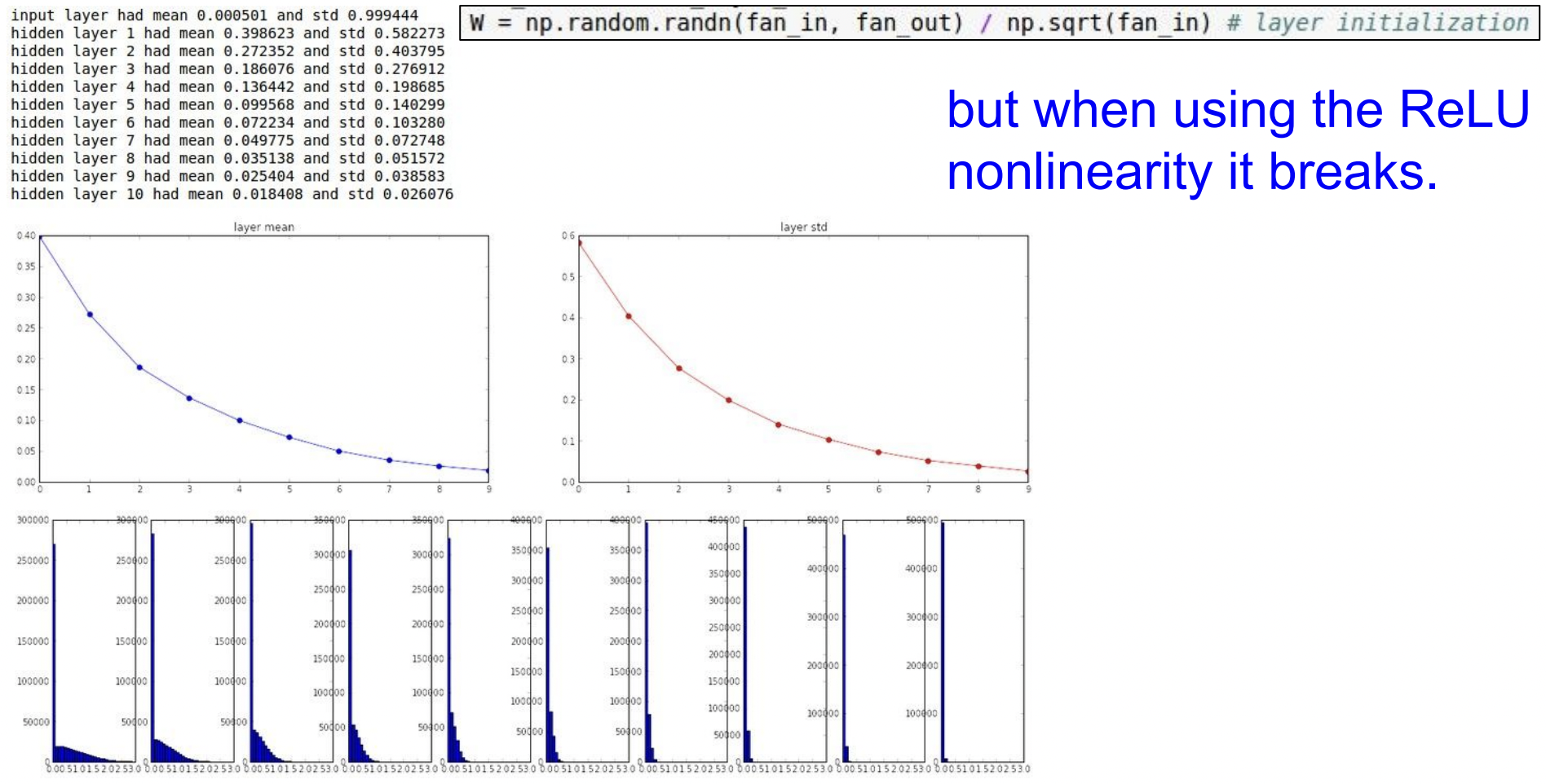
하지만 비선형인 ReLU를 쓰면 잘 동작하지 않는다는 문제가 있다. ReLU는 출력의 절반이 죽기 때문에 그 절반은 매번 0이 되어버려서 학습할수록 점점 더 많은 값들이 0이 되고 결국은 deactivated 된다. (맨 아래 쪽을 보면 분산도 반토막 나는걸 볼 수 있다.)

그래서 이 문제를 해결하기 위해 추가적으로 2를 더 나눠주는 방법을 제안한 논문이 있다. 뉴런 반절이 죽는다는 것을 고려해 2로 나눠주고 실제로 잘 동작한다.

W = np.random.randn(fan_in, fan_out) / np.sqrt(fan_in / 2)

Batch Normalization

“What we want? 각 층의 출력값이 unit gaussian → just make them so 🔥”

현재 batch 단위로 한 레이어에 입력으로 들어오는 모든 값들을 이용해서 mean과 variance를 구할 수 있다. 이것을 이용해서 normalizaiton이 가능하다. 이렇게 만들어진 함수를 보면 미분 가능하고 backprop이 가능하다(평균과 분산이 constant(상수)) .

⓵ 각 feature element 별로 평균과 분산을 각각 구한다

⓶ 한 batch내에서 이걸 전부 계산해 normalize한다.

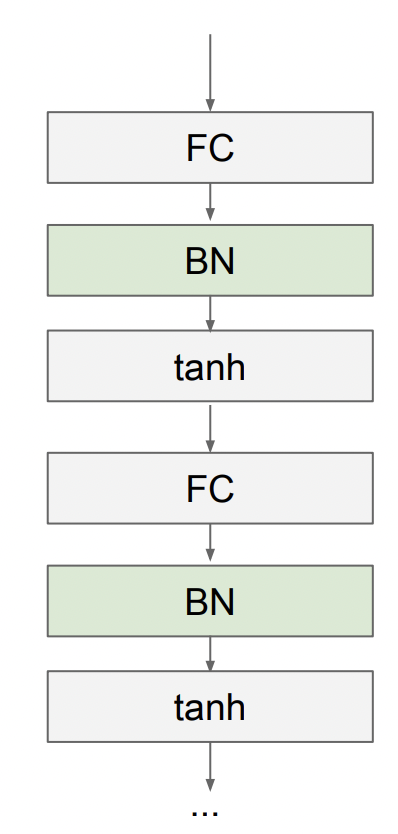
보통 Batch Normalization 연산은 FC or Conv Layer 직후에 들어간다.

앞선 깊은 네트워크에서는 각 층의 $W$ 를 연속적으로 곱해서 ‘bad scaling effect’ 가 발생 했었는데 normalization은 그 bad effect를 상쇄시킨다.

Batch Normalization 은 입력의 스케일만 살짝 조정해주는 역할이기 때문에 FC와 Conv 어디에든 적용할 수 있다.

차이점이 있다면 Conv Layer 에서는 normalization 을 차원(feature dimension)마다 독립적으로 수행하는 것이 아니라 같은 activation map의 같은 채널에 있는 요소들은 같이 normalize 해준다는 것이다. 왜냐면 Conv 특성상 같은 방식으로 normalize 시켜야 하기 때문이다.

그래서 Conv Layer의 경우 activation map(채널, Depth)마다 평균과 분산을 하나만 구한다. 그리고 현재 batch에 있는 모든 데이터로 normalize 해준다.

💢 Problem : do we necessarily want a unit gaussian input to a tanh layer?

Batch Normalization은 입력이 tanh의 linear 한 영역에 존재하도록 강제하기 때문에 이러면 saturation이 전혀 일어나지 않게 된다. 이것보다는 우리가 얼마나 saturation이 일어날지를 조절하는 것이 더 좋다.

Batch Normalization 에서는 Normalization 연산에 scaling 연산을 추가한다. 이를 통해 unit gaussian으로 normalize 된 값들을 $\gamma$ 로는 스케일링의 효과를, $\beta$ 로는 이동의 효과를 준다.

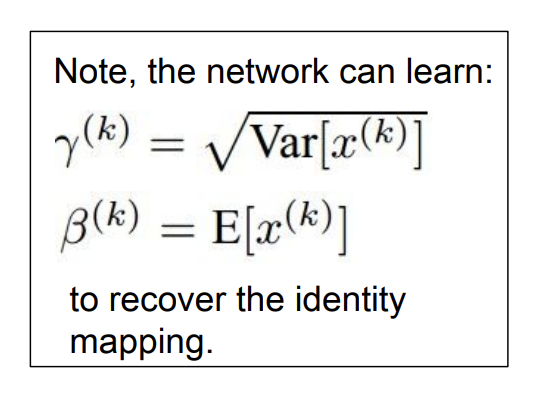
Normalized 된 값들을 원상복구 할 수 있는데 $\gamma$ = 분산, $\beta$ = 평균 값을 넣어주면 된다. 그러면 네트워크가 데이터를 tanh에 얼마나 saturation 시킬지를 학습하기 때문에 우리는 ‘flexibility’ 을 얻을 수 있다.

Summarize BN

입력이 있고 모든 mini-batch 마다 각각 에서의 평균과 분산을 계산한다. 그리고 평균과 분산으로 normalize한 후에 다시 추가적인 scaling, shifting factor를 사용한다.
BN은 gradient의 흐름을 보다 원활하게 해주며 결국 학습이 더 잘되게(robust) 해준다.
BN을 쓰면 learning rate를 더 키울 수 있고 다양한 초기화 기법들을 사용해 볼 수 있다.

→ Reason we need to use Batch Normalization 👍

💡Batch Normalization은 regularization 역할도 한다

각 층의 출력은 해당 데이터 하나 뿐만 아니라 batch 안에 존재하는 모든 데이터들의 영향을 받는다.(평균, 분산) 왜냐면 각 층의 입력은 해당 batch 의 (표본)평균으로 normalize 되기 때문이다. 그렇기 때문에 이 층의 출력은 이제 오직 하나의 샘플에 대한 deterministic 한 값이 아니게 되고 batch 내의 모든 데이터가 입력으로 한대 묶인다고 볼 수 있다.

그래서 레이어의 출력은 deterministic하지 않고 조금씩 바뀌게 되고 이는 regularization effect를 준다.

Babysitting the Learning Process

이제는 학습과정을 어떻게 모니터링하고 하이퍼파라미터를 조절한 것인지 살펴보자.

Step 1 : Preprocess the data

Step 2: Choose the architecture

예시로 하나의 Hidden layer와 50개의 뉴런을 가진 모델로 해보자. (다른 모델도 상관없음)

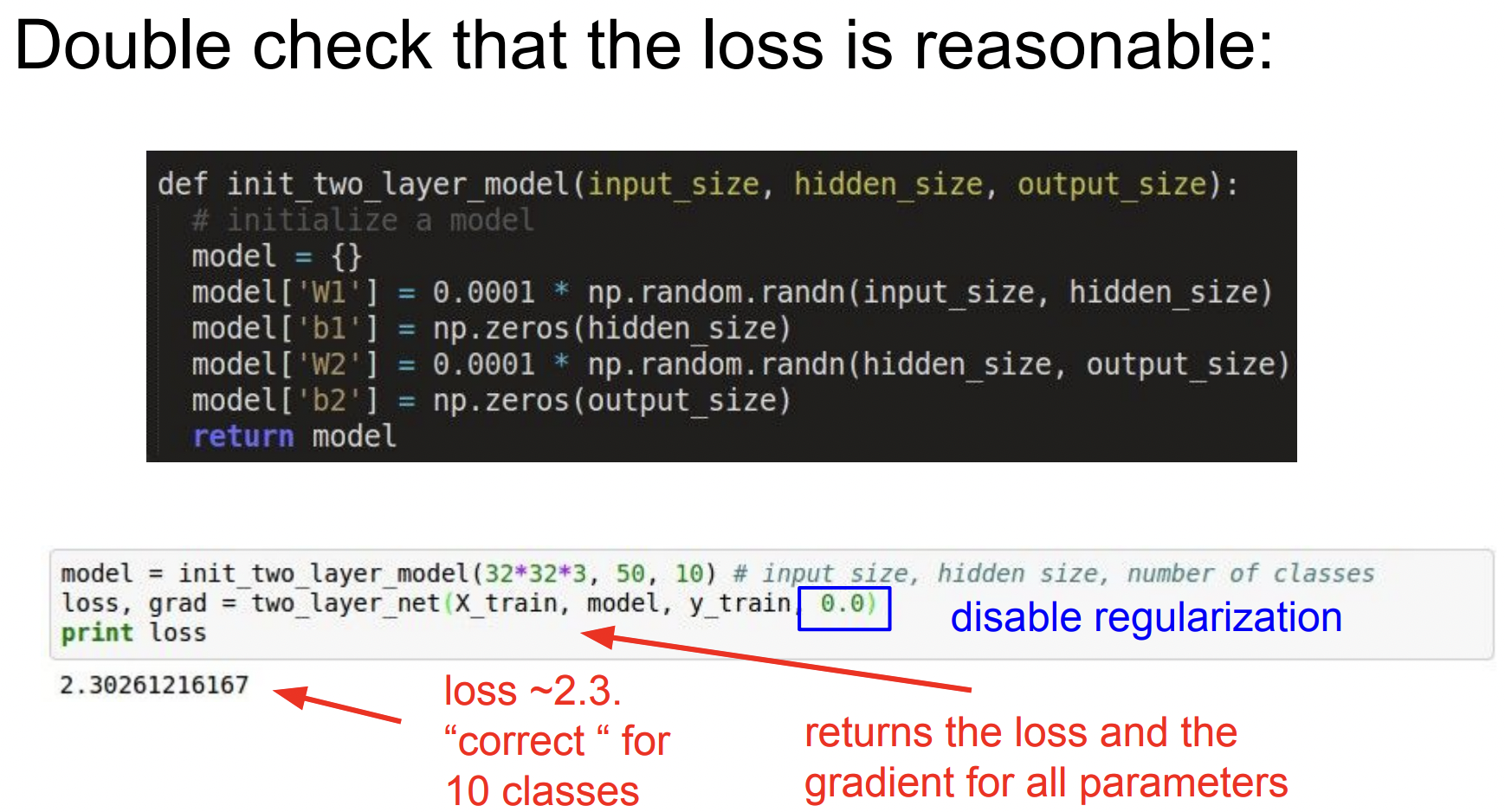
이제 해야할 일은 네트워크를 initialization 시키는 것❗️(Forward pass 후에 loss는 reasonable 해야함.)

softmax classifier의 loss는 negative log likelihood가 되어야 한다.

(가령 10개의 클래스라면 Loss는 $-log(1/10)$ 이 될 것임) (아래에서는 대략 2.3정도) → Good sanity check

앞 계산에서는 regularization을 사용하지 않은 상태이다. 여기에 regularization을 추가하면 손실함수에 regularization term이 추가되기 때문에 Loss가 증가한다. → Good sanity check

이제 준비가 끝났으니까 학습을 시작해보자.

먼저 처음 시작할 때는 데이터의 일부만 우선 학습시켜 보면 좋다. 그러면 데이터가 적기 때문에 overfit이 생길 것이고 loss가 많이 줄어들 것이기 때문이다. 아래는 regularization을 사용하지 않았고 결과를 보면 loss는 줄어들고 accuracy는 1.0으로 점점 증가한다. (데이터가 작은 경우라면 모델이 완벽하게 데이터를 overfit 할 수 있어야 한다.)

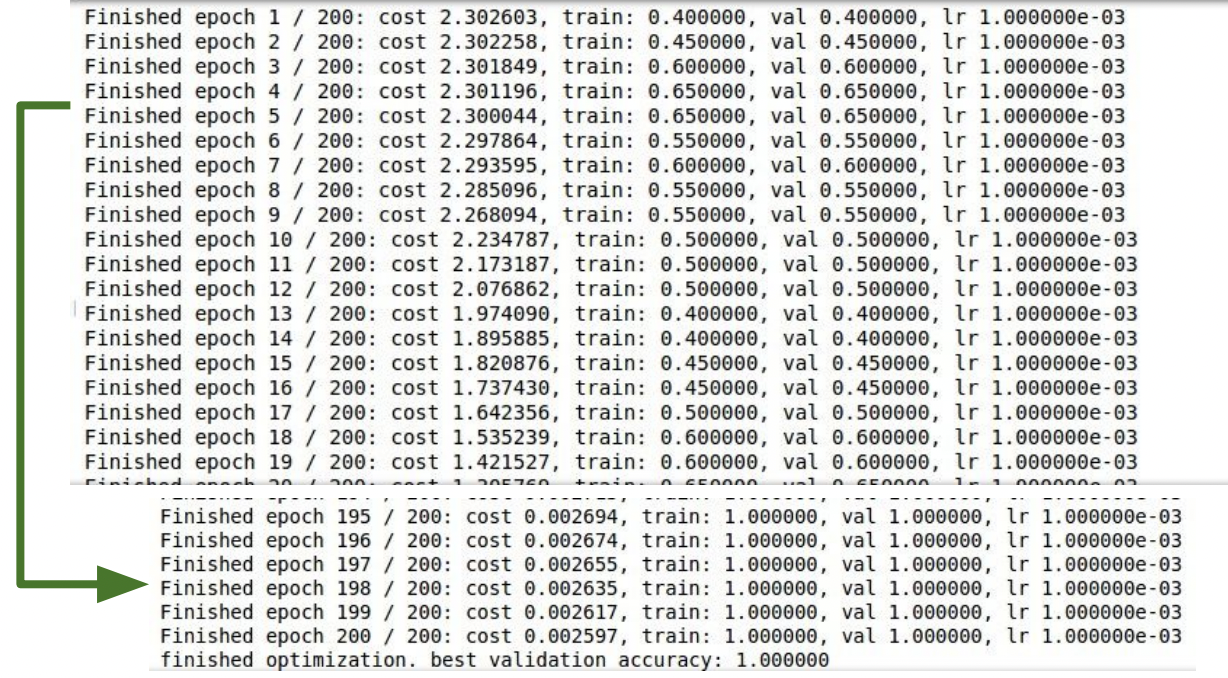
👊 이제 정말 학습을 시작할 차례이다.

전체 데이터셋을 사용하고 regularization을 약간 주면서 적절한 learning rate를 찾아야 한다.

우선 learning rate 몇가지를 정하고 실험해 보자.

먼저 아래에서는 1e-6으로 정했다. 결과를 보면 Loss가 잘 줄어들지 않는데 가장 큰 이유는 learning rate가 지나치게 작아서 gradient 업데이트가 충분히 일어나지 않게 돼서 cost가 변하지 않기 때문 이다.

BUT loss가 잘 변하지 않음에도 training/validation accuracy가 20%까지 급상승한다.

👀 WHY?

확률 값들은 diffuse하기 때문에 loss는 잘 변하지 않는다. 하지만 이 확률은 우리가 지금 ‘학습’하고 있기 때문에 조금씩 ‘옳은’ 방향으로 바뀌고 있다. 

그래서 가중치는 서서히 변하지만 accuracy는 그저 가장 큰 값만 취하기 때문에 급격히 증가할 수 있다.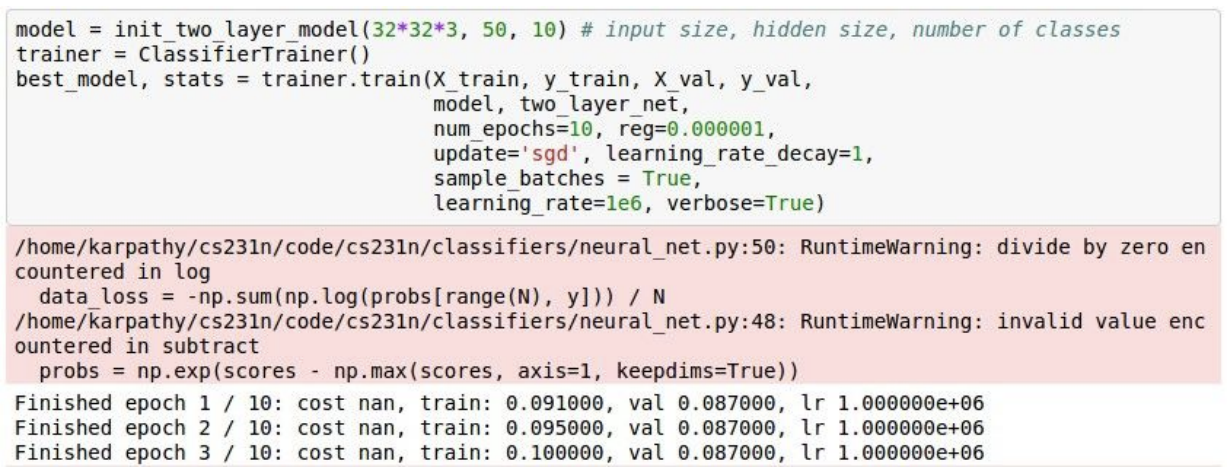

이제 learning rate을 더 큰 값인 1e6으로 바꿔보자.
결과를 보면 cost가 NaN이다. 즉, learning rate가 지나치게 높아서 cost가 발산(exploded)한 것이다. 이런 경우에는 learning rate을 낮춰야 하는데 3e-3으로 해도 여전히 발산한다.

보통 learning rate은 $[1e-3 , 1e-5]$ 사이의 값을 사용해서 cross-validation을 수행해 준다.

Hyperparameter Optimization

전략 1. Cross-validation

단계적으로 hyperparameter를 찾는다.

⓵ coarse stage에서는 넓은 범위에서 값을 고른다. Epoch 몇번 만으로도 현재 값이 잘 동작하는지 알 수 있다. (NaN 출력 or Loss가 줄지 않는 등을 보면서 이에 따라 적절히 잘 조절) Coarse stage가 끝나면 어느 범위에서 잘 동작하는지를 대충 알게 될 것이다.

⓶ fine stage에서는 좀 더 좁은 범위를 설정하고 학습을 좀 더 길게 시켜보면서 최적의 값을 찾는다.

tip으로 train 동안에 cost가 어떻게 변하는지를 살펴보면 NaN으로 발산하는 징조를 감지할 수 있다. 이전의 cost보다 더 커지거나 한다면(가령 cost가 이전보다 3배 높아졌다거나,,) 잘못하고 있는 것이다. cost가 엄청 크고 빠르게 오르고 있다면 loop를 멈춰버리고 다른 하이퍼파라미터를 선택하면 된다.

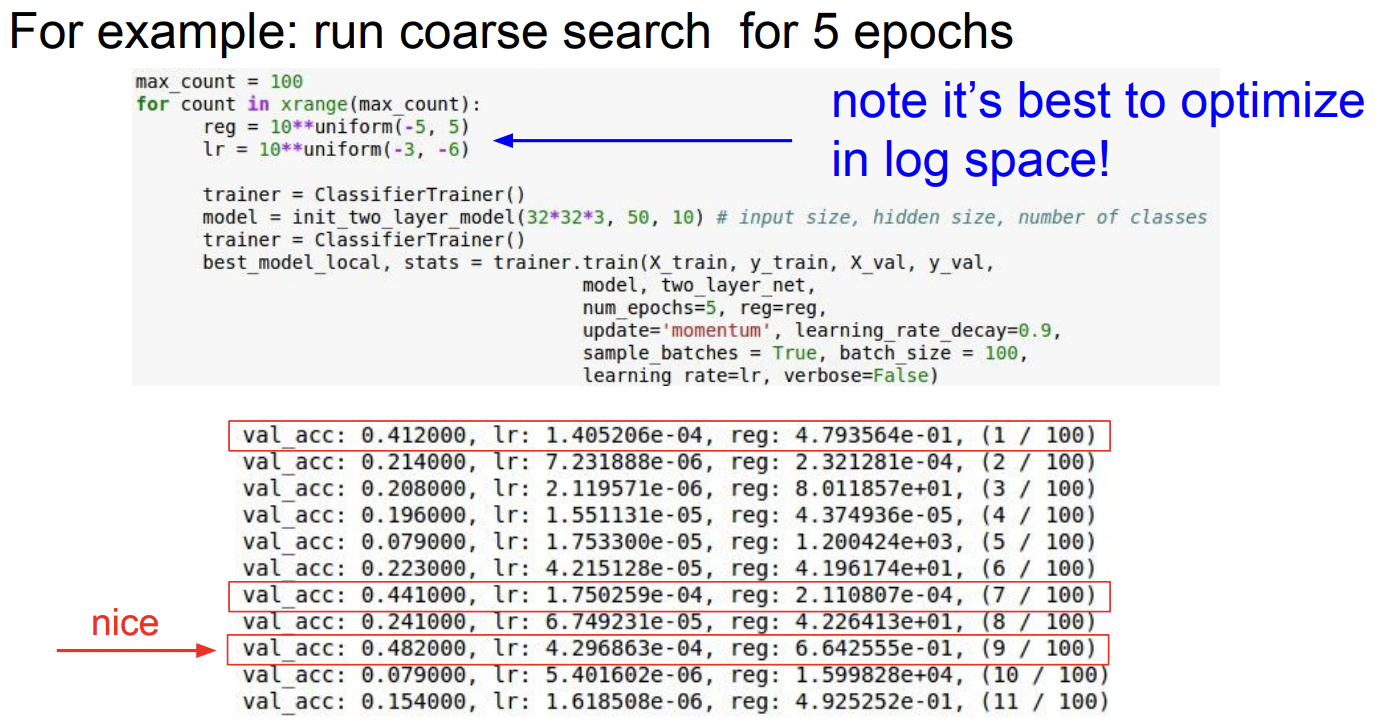
예시를 봐보면 아래는 5 epochs을 돌며 ⓵ coarse search를 하는 과정이다. 앞선 네트워크와 구조는 유사하고 validation accuracy를 잘 살펴봐야한다. 빨간 박스는 높은 val_acc이고 이 지역이 바로 fine-stage를 시작할 만한 범위가 될 것이다. (또한 하이퍼파라미터 최적화 시에는 Log scale로 값을 주는 것이 좋다. )

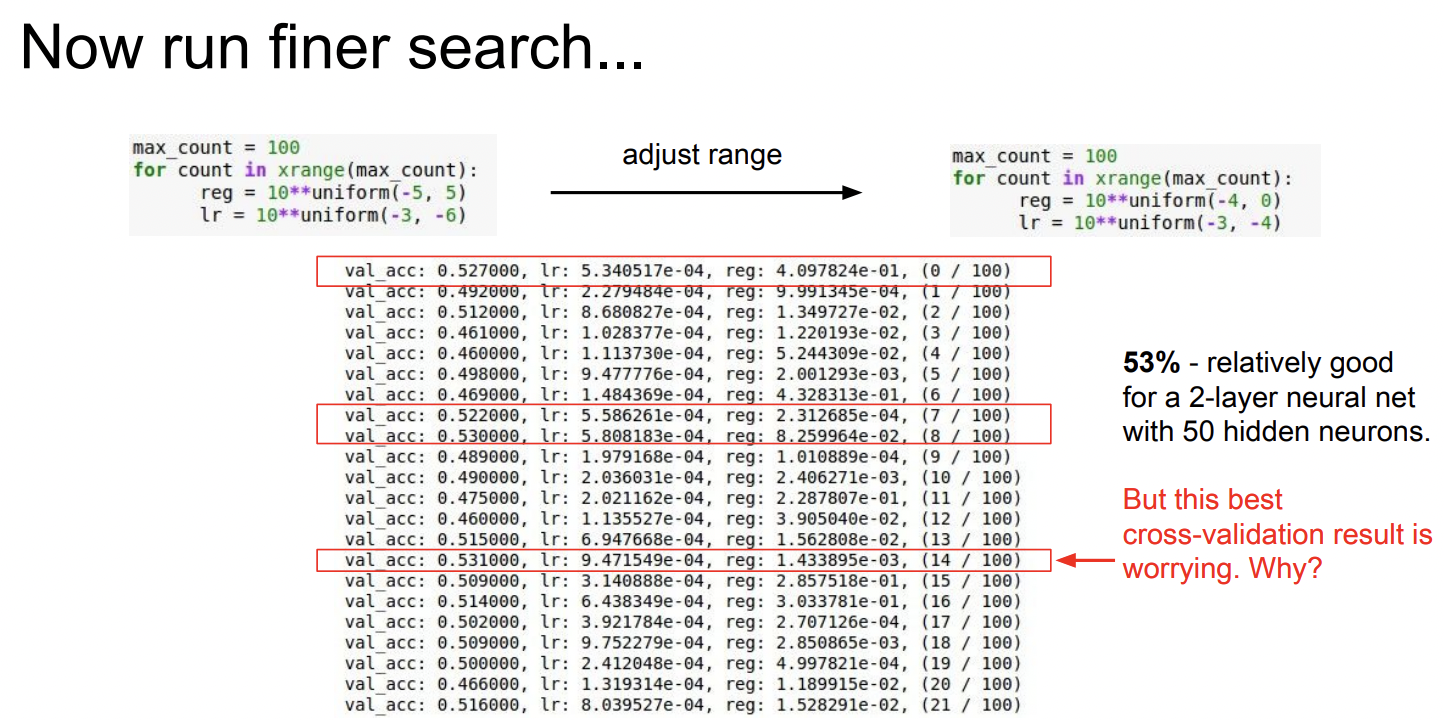
범위를 다시 조절해 reg 범위를 $[10^-4, 10^0]$ 정도로 좁혔다 ⓶ fine-tuning. 이 범위에서 53%의 val_acc를 보이는 걸 알 수 있고 이 구간이 학습이 가장 잘 되는 구간이 될 것이다.

💢 But there is problem!

우리는 best accuracy를 찾았는데 잘 보면 good learning rates는 전부 10e-4 사이에 존재하고 있다. 즉 learning rate의 최적값들이 우리가 다시 좁혀 설정한 범위의 경계부분에 집중되어 있다는 것을 알 수 있다.

💢 This is bad!!

왜냐면 이렇게 되면 최적의 learning rate를 효율적으로 탐색할 수 없을 수도 있기 때문이다. 탐색 범위를 조금 이동시킨다면 더 좋은 범위를 찾을 수 있을지도 모른다.
그래서 우리는 최적의 값이 정해진 범위의 중앙 쯤에 위치하도록 범위를 잘 설정해 주는 것이 중요하다.

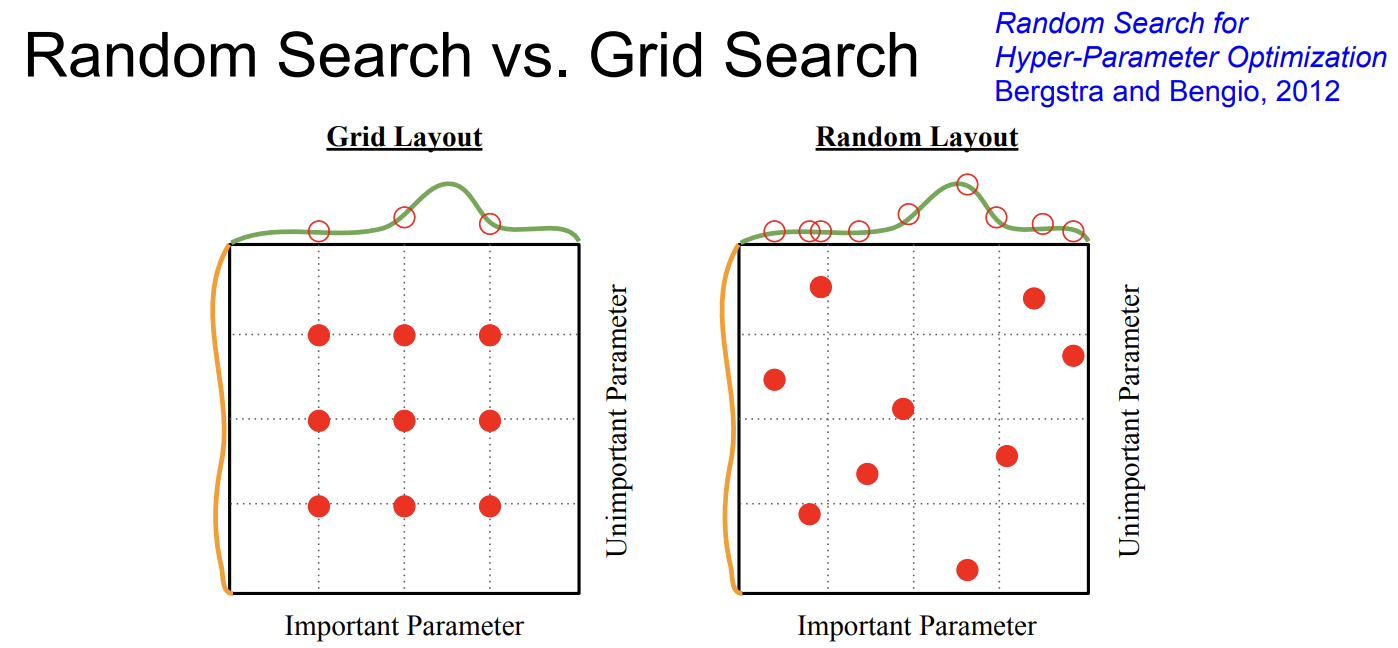
전략 2. Grid search를 이용

Grid search는 하이퍼 파라미터를 고정된 값의 간격으로 샘플링하는 것인데 실제로는 grid search보다 이전처럼 random search 하는 것이 더 좋다.

Loss curve & Accuracy

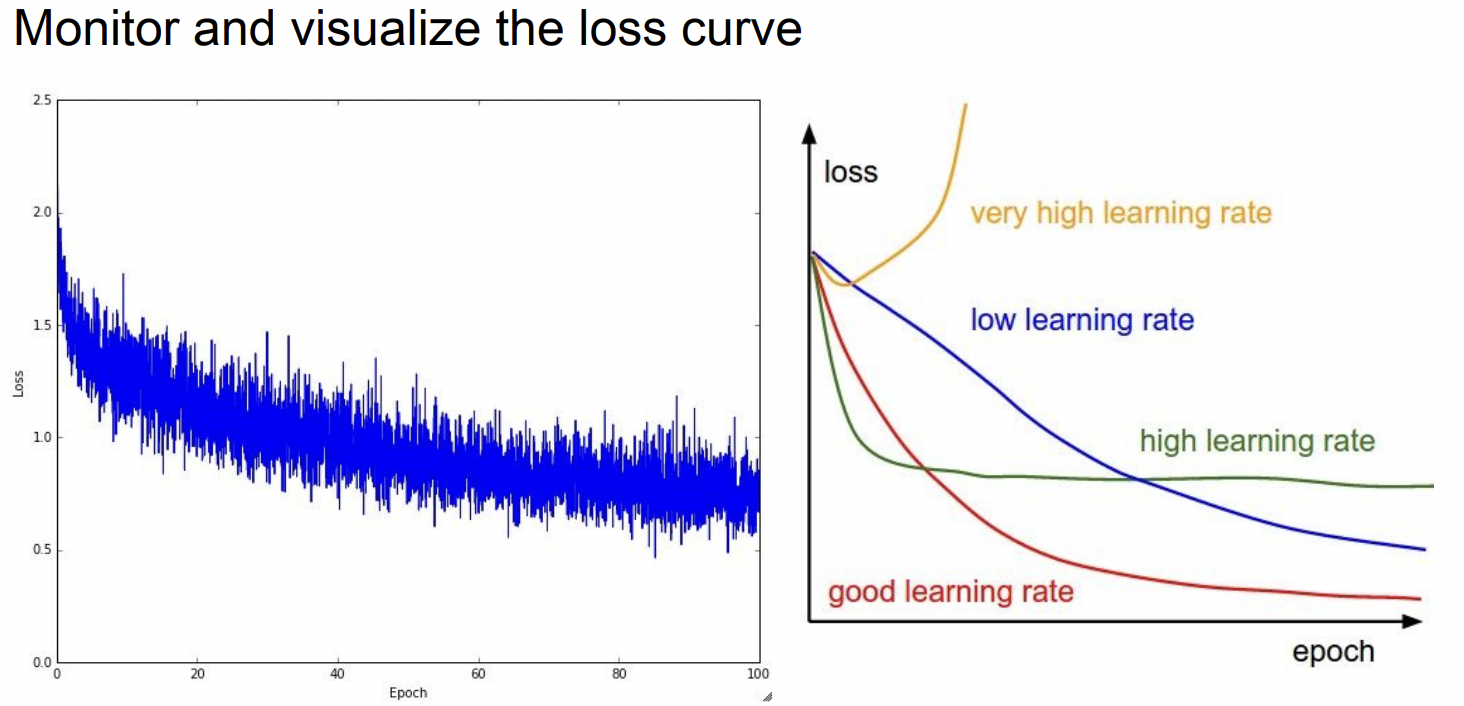
앞에서 말했듯이 loss curve를 모니터링 하는데 있어서 learning rate이 정말 중요하다.

loss가 발산하면 learning rate이 높은 것이고 너무 평평하면(linear) 너무 낮은 것이다. 그리고 가파르게 내려가다가 어느 순간 정체기가 생기면 이 또한 여전히 너무 높다는 의미이다. Learning step이 너무 크게 점프해서 적절한 local optimum에 도달하지 못하는 경우이다.

최적의 learning rate은 대게 파란색 그래프와 같이 비교적 가파르게 내려가면서도 지속적으로 잘 내려가는 것이다.

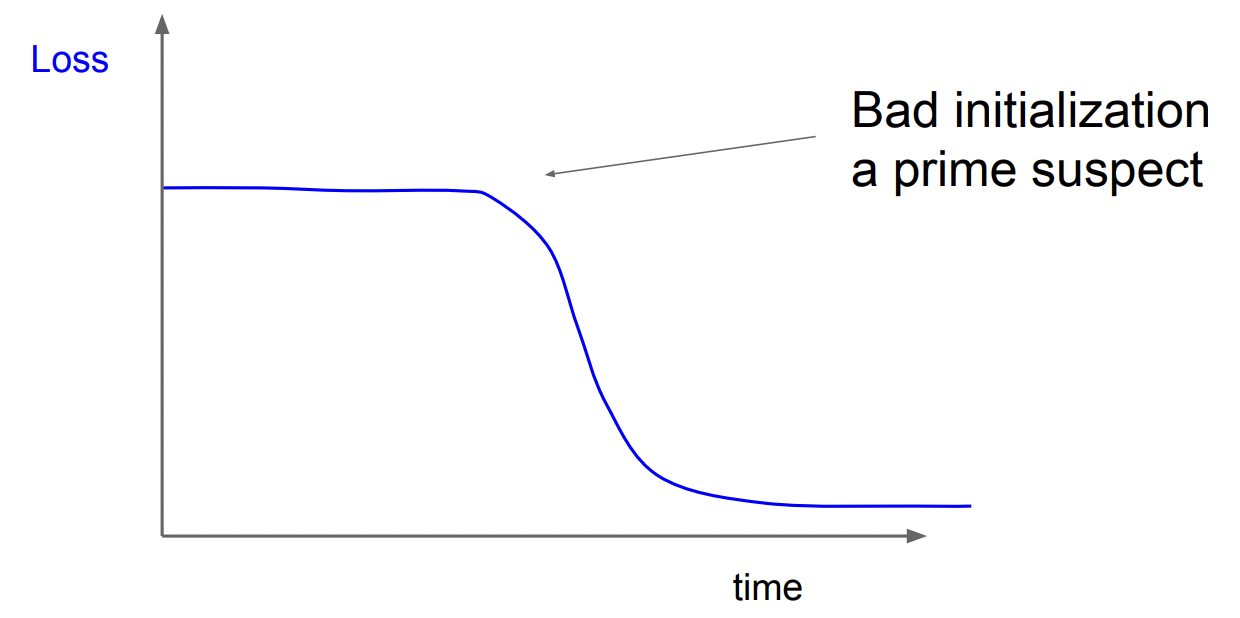
아래처럼 loss가 평평하다가 갑자기 가파르게 내려가는 것을 보게 된다면 이는 초기화의 문제일 수 있다. gradient의 backprop이 초기에는 잘 되지 않다가 학습이 진행되면서 회복이 되는 경우이다.

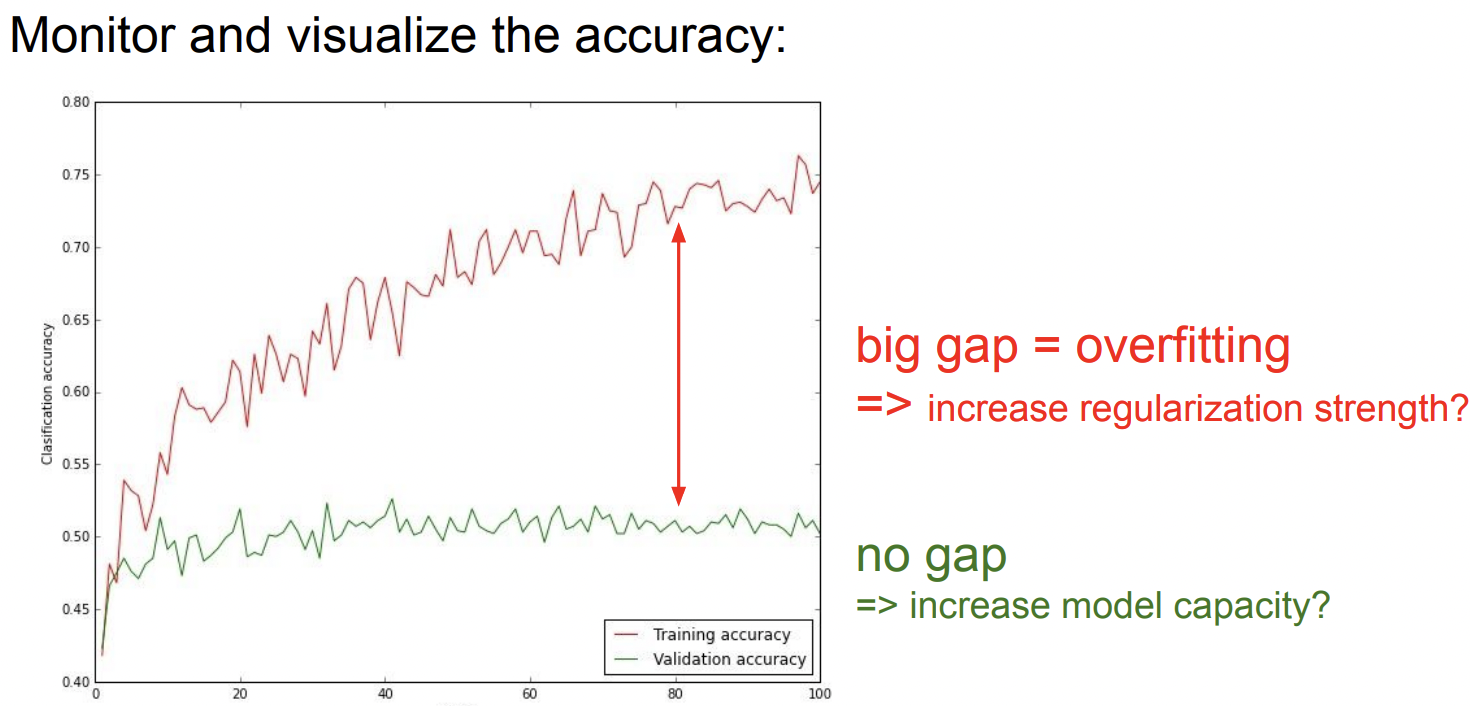
그리고 accuracy를 모니터링 할 때 train_acc과 val_acc이 big gap을 보인다면 overfitting 문제일 수 있으니 regualrization의 강도를 높혀야 할 수도 있다.

그리고 gap이 없다면 아직 overfit하지 않은 것이고 capacity를 높힐 수 있는 충분한 여유가 있다는 것을 의미한다.

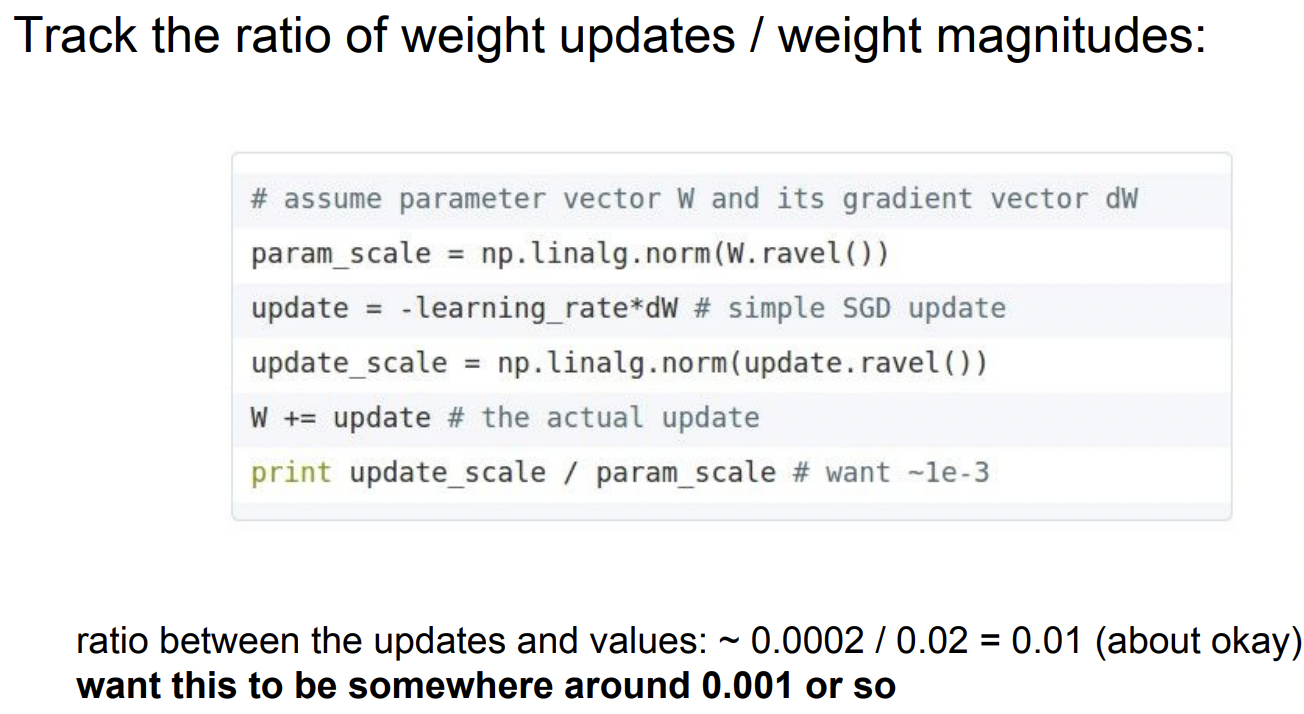
Weight updates / weight magnitudes

우선 파라미터의 norm을 구해서 가중치의 규모를 계산하고 업데이트 사이즈 또한 norm을 통해 구할 수 있고 이로 얼마나 크게 업데이트 되는지를 알 수 있다. 우리는 이 비율이 대략 0.001 정도 되길 원한다. (이 값은 변동이 심해 정확하지 않을 수 있다. 하지만 업데이트가 지나치게 크거나 작은지에 대한 감을 어느정도 가질 수 있다. )
업로드중..

Eunjin Kim

ALL IS WELL🌻

이전 포스트