진도: Chapter 06
기본 숙제(필수): k-평균 알고리즘 작동 방식 설명하기
추가 숙제(선택): Ch.06(06-3) 확인 문제 풀고, 풀이 과정 정리하기
서론
저번주는 여름 방학이라 쉬었더니 너무너무 좋았다. 다시 충전이 된 느낌이다. 마지막 주차까지 꾸준히 달려서 마무리 해보자!ㅎㅎ
6. 비지도 학습
6-1. 군집 알고리즘
드디어 비지도 학습이다!!
미리 정답을 알 수 없을때 하는 방법, 타깃을 모를때 쓰는 방법이다.
비지도 학습 (Unsupervised learning)
타깃이 없을 때 사용하는 머신러닝 알고리즘
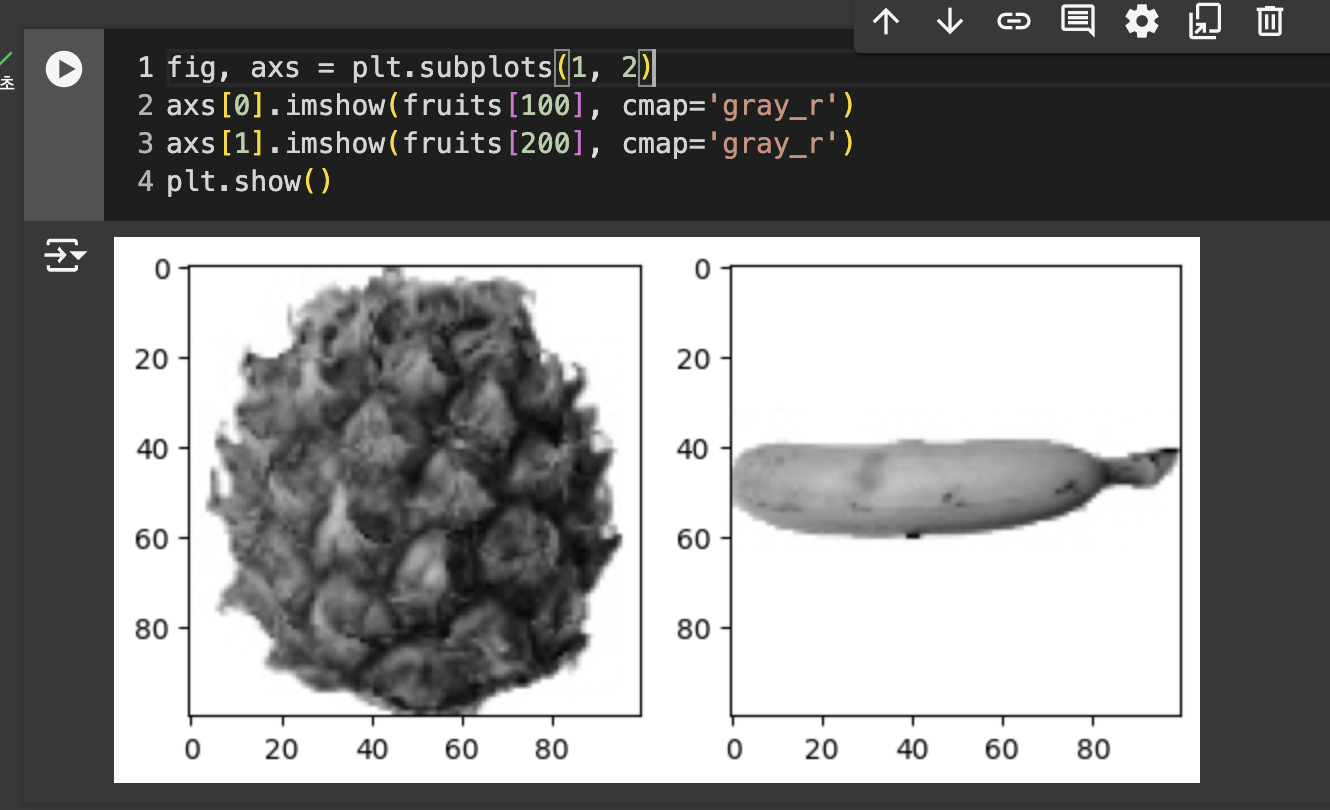
첫 번째 차원(300) : 샘플의 개수
두 번째 차원(100) : 이미지 높이
세 번째 차원(100) : 이미지 너비
즉, 크기는 100 X 100
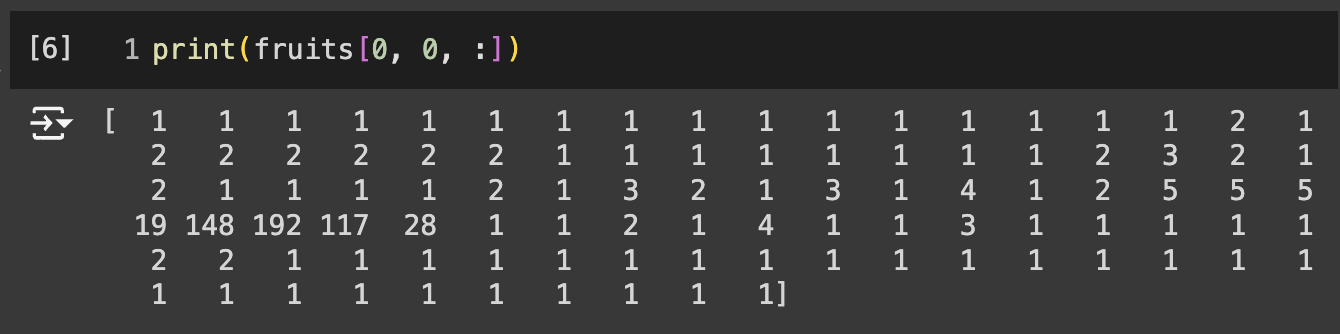
흑백 사진이므로 0~255 사이의 정수값을 가진다.
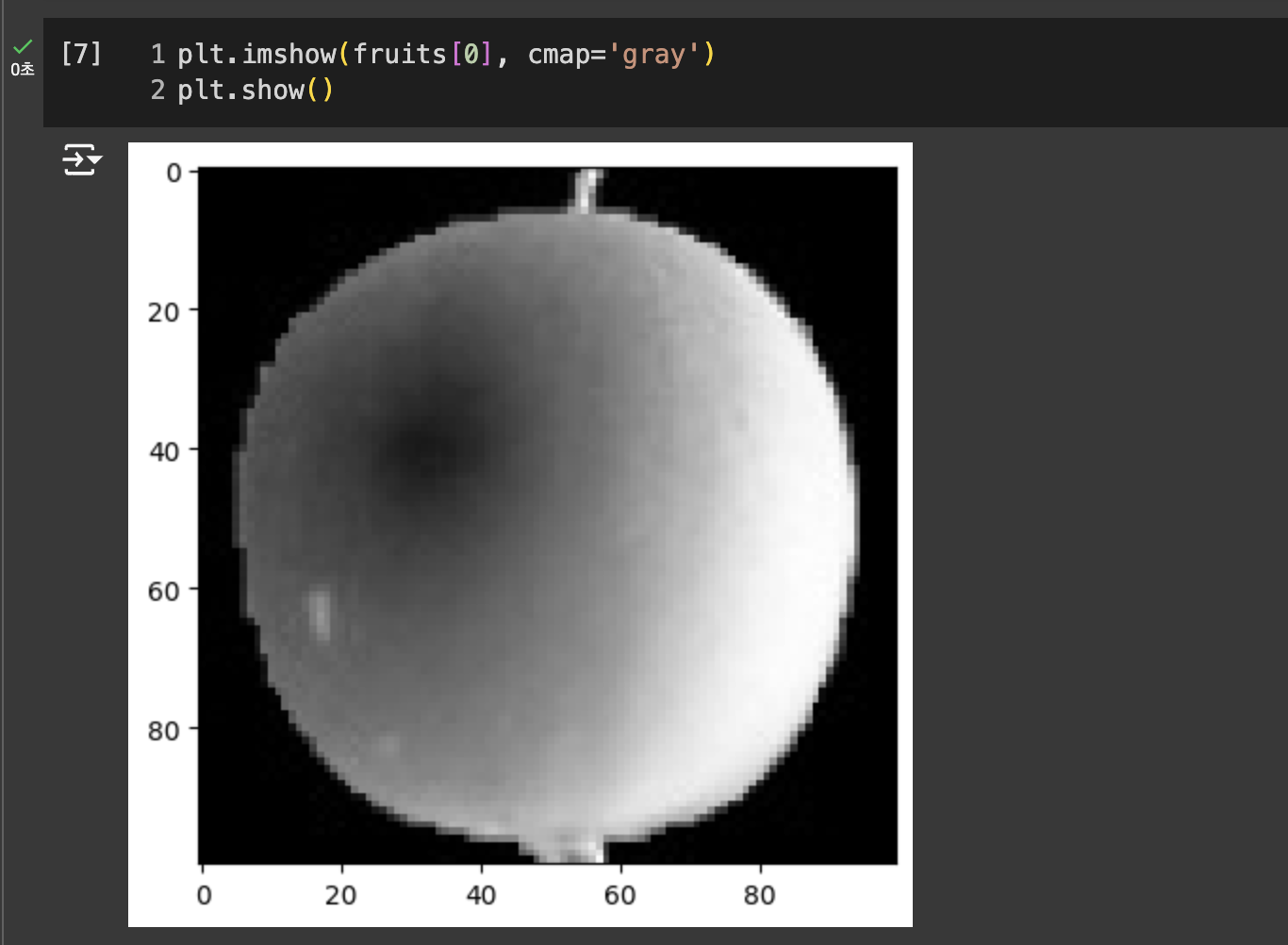
0에 가까울 수록 검게 나타나고, 높은 값은 밝게 표시된다.
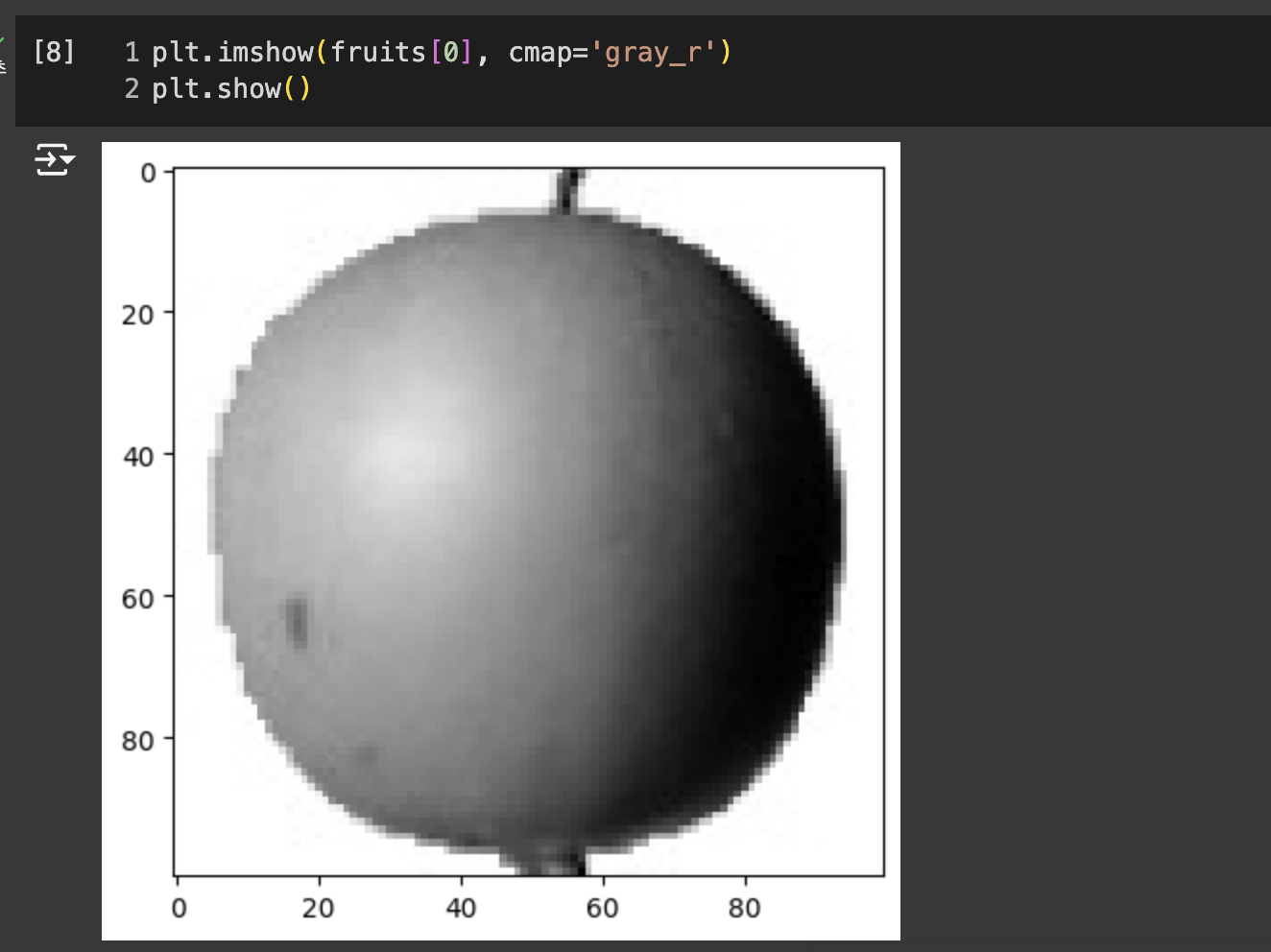
이 이미지는 넘파이 배열로 반환할 때 반전시킨것. 흰 바탕이 높은 값인데 실제 사과가 있는 부분은 짙다. 하지만 중요한 관심 부분은 바탕이 아닌 사과이므로 대상을 밝게 반전 시킨 값이 의미 부여하기 좋다.
- 각 과일에 대한 1차원 배열을 만든다.
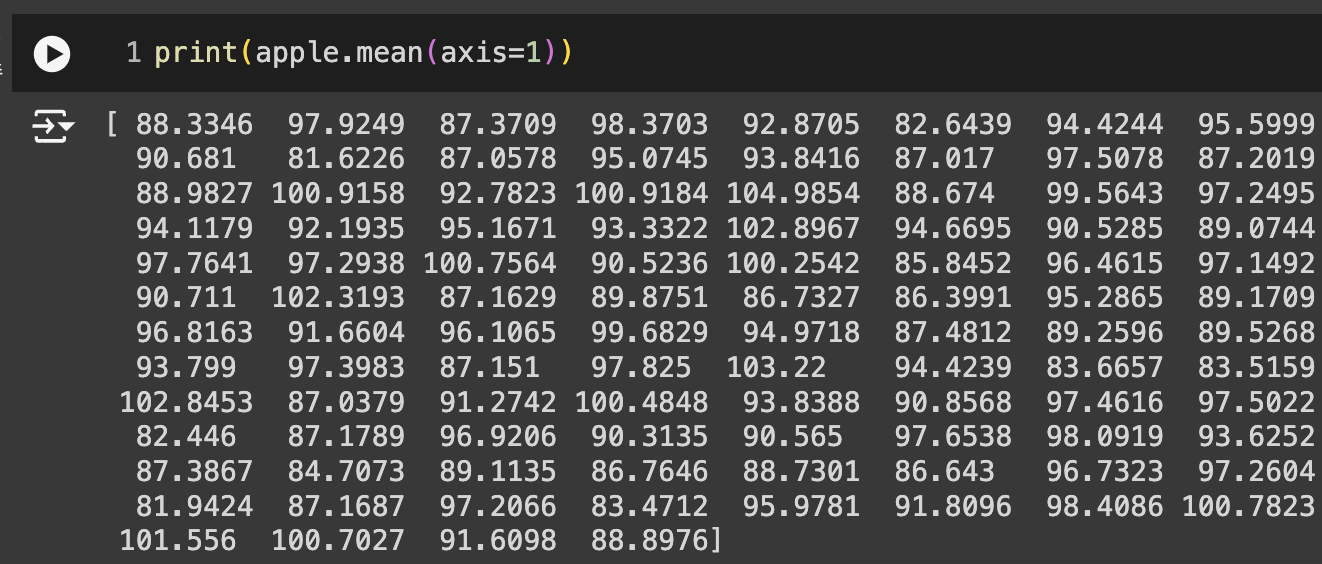
- 100개에 대한 각 샘플의 픽셀 평균값 계산

- 바나나의 평균값 40 아래
- 파인애플과 사과는 90~100 사이
픽셀값만으로는 파인애플과 사과를 구분하기 어려움
-> 샘플의 평균값이 아니라 픽셀별 평균값을 비교
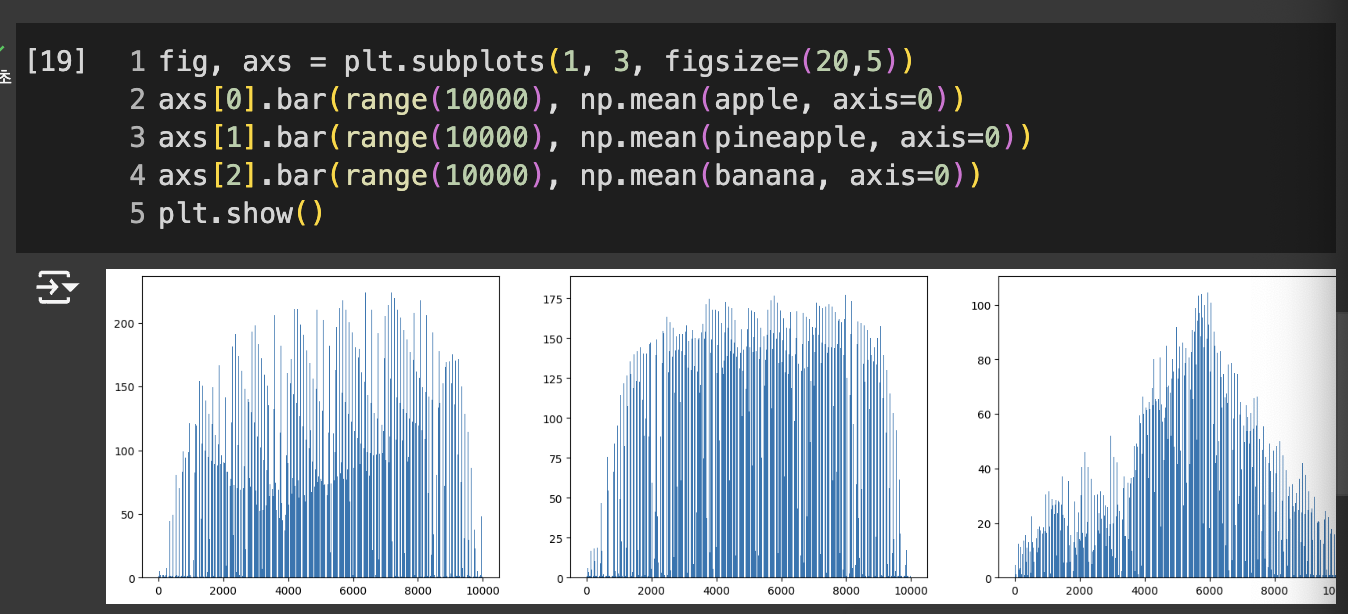
- 사과는 사진 아래쪽으로 갈수록 값이 높아진다.
- 파인애플은 비교적 고르면서 높다.
- 바나나는 중앙의 픽셀값이 높다.




- 절대값 오차 사용하여 apple_mean과 가장 가까운 사진 선택
군집 : 비슷한 샘플끼리 그룹으로 모으는 작업
클러스터 : 군집 알고리즘에서 만든 그룹

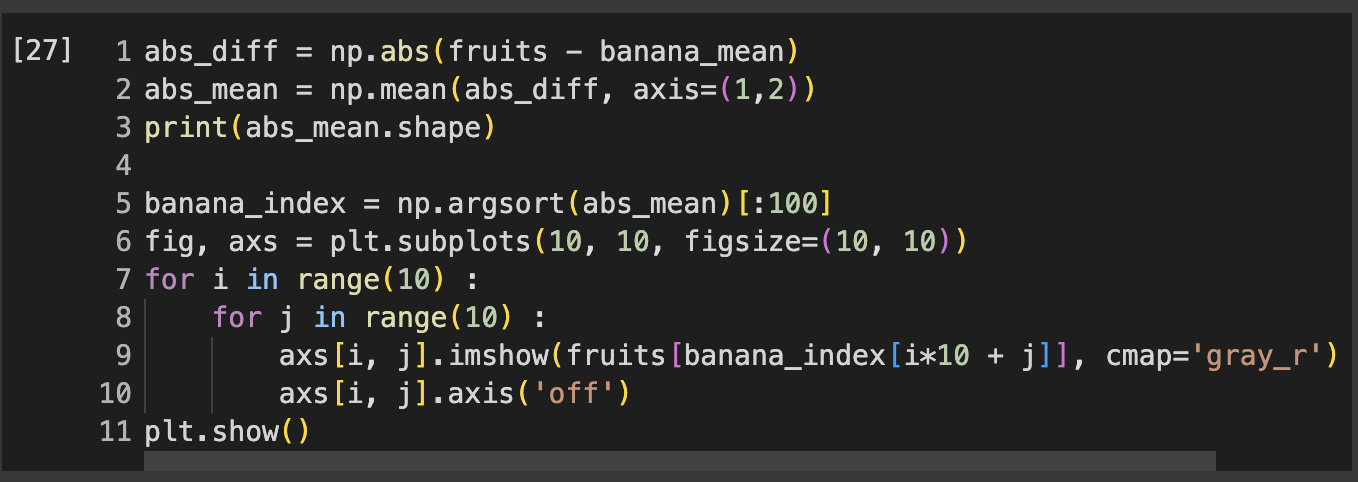

-> 마지막 2개가 바나나가 아닌 사과가 나온다. 다 찾을 수 없었다...
06-2. k-평균
위 과일들은 어떤 사진인지 알고 있어서 평균을 구할 수 있었다.
하지만 진짜 비지도 학습에서는 어떤 과일인지 모른다.
이때 K-평균 군집 알고리즘을 사용하면 평균값을 자동으로 찾아준다.
평균값이 클러스터의 중심에 위치하기 때문에 클러스터 중심 또는 센트로이드라고 부른다.
K-평균 알고리즘
- 무작위로 k개의 클러스터 중심을 정한다
- 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정
- 클러스터에 속한 샘플의 평균값으로 클러스터의 중심을 변경
- 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복
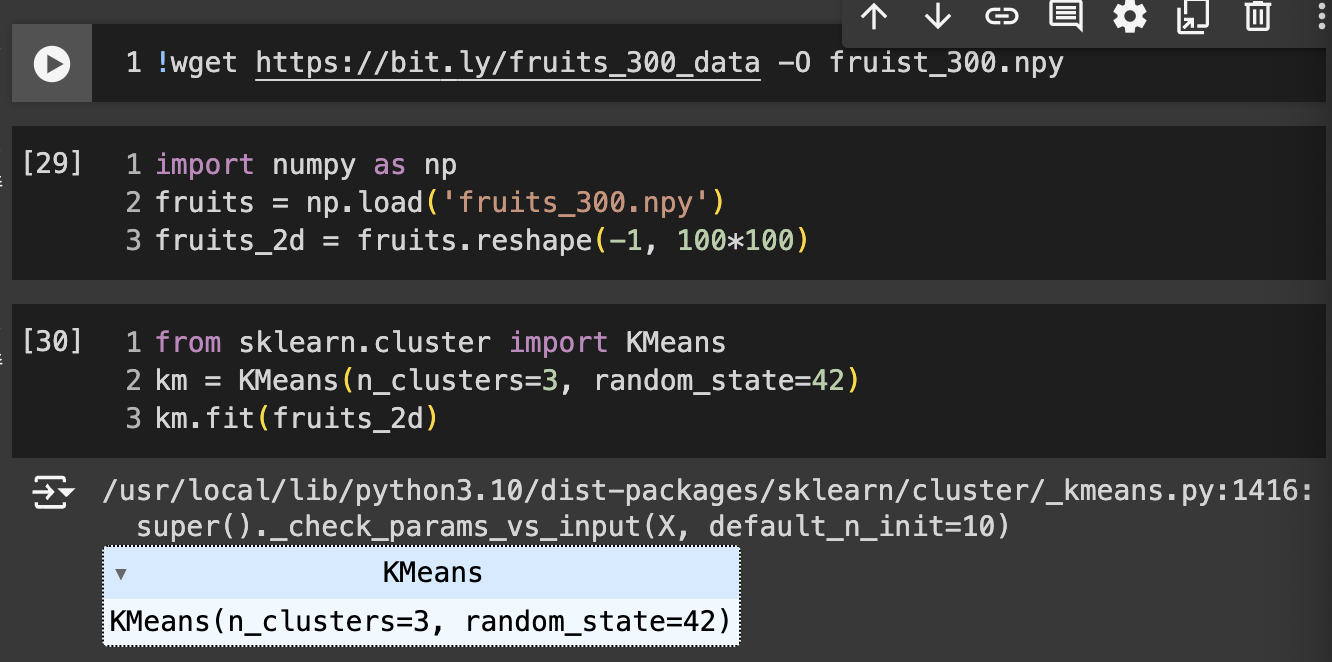
- wget : 데이터 다운로드
- np.load() : 넘파이 배열 준비
- KMeans : K-평균 알고리즘
- n_clusters : 클러스터 개수 지정

- labels_ : 군집된 결과 저장.

- draw_fruits() : 3차원 배열을 입력받아 가로로 10개씩 이미지를 출력하는 함수


- km.labels_ == 0 : 0인 값의 위치를 True, 그 외에는 False가 되어 불리언 인덱싱




클러스터 중심
clustercenters 속성에 저장

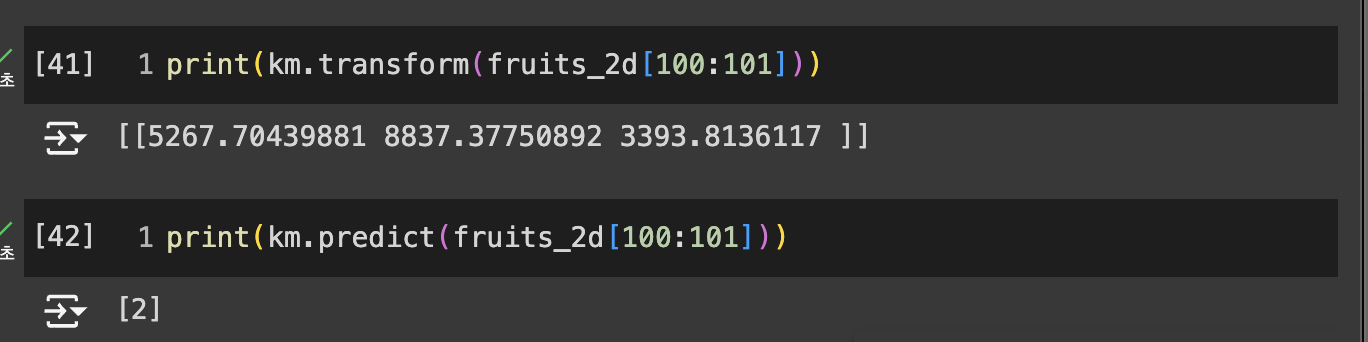
- transform() : 훈련 데이터 샘플에서 클러스터 중심까지의 거리 변환
- 1, 2, 3번째 클러스타까지의 각각의 거리. 세번째 클러스터까지의 거리가 가장 적다
- predict() : 가장 가까운 클러스터 중심을 예측 클래스로 출력
클러스터 중심을 옮기는 것을 반복하며 최적의 클러스터를 찾음
- niter : 알고리즘이 반복한 횟수
최적의 K 찾기
엘보우(elbow) : 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수를 찾는 방법
이너셔(inertia) : 클러스터의 중심과 클러스터에 속한 샘플 사이의 거리의 제곱 합
- 클러스터 개수 늘면 -> 개개의 크기는 줄어들어 이너셔도 줄어든다.
- 클러스터 개수 증가시키면 -> 이너셔 감소하는 속도가 꺾이는 지점이 있다
- 이 지점이 마치 팔꿈치 모양이어서 엘보우 방법이라 부름.
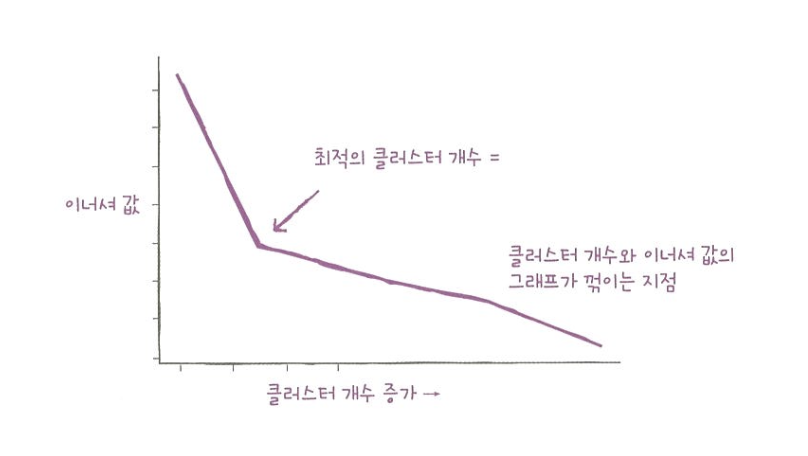
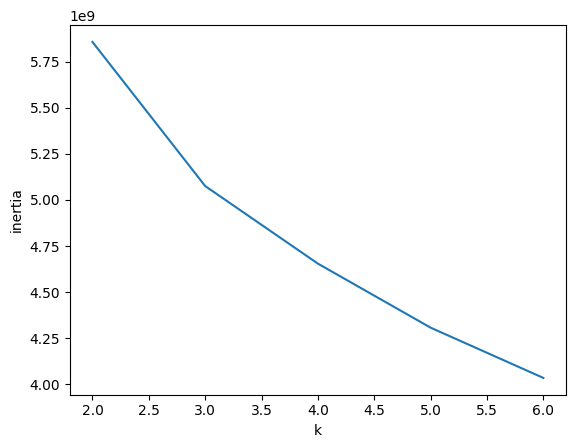
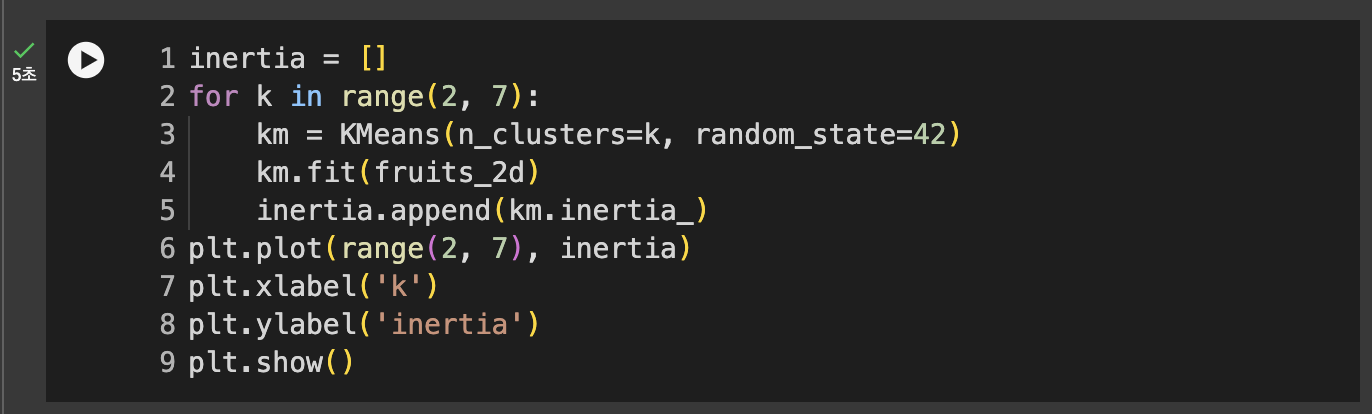
- k=3에서 기울기가 바뀐것을 볼 수 있다.

06-3. 주성분 분석
차원과 차원 축소
- 특성 = 차원(dimension)
- 특성을 줄이면 저장 공간 절약 가능
차원 축소(dimensionally reduction) 알고리즘
- 데이터를 가장 잘 나타내는 일부 특성 선택하여 데이터 크기 줄임
- 원본 차원으로 손실을 최대한 줄이면서 복원 가능
- 대표적인 차원 축소 알고리즘 = 주성분 분석(principal component analysis)
- PCA 라고도 부름
주성분 분석 소개
-
데이터에 있는 분산이 큰 방향을 찾는 것
-
분산 : 데이터가 널리 퍼져있는 정도
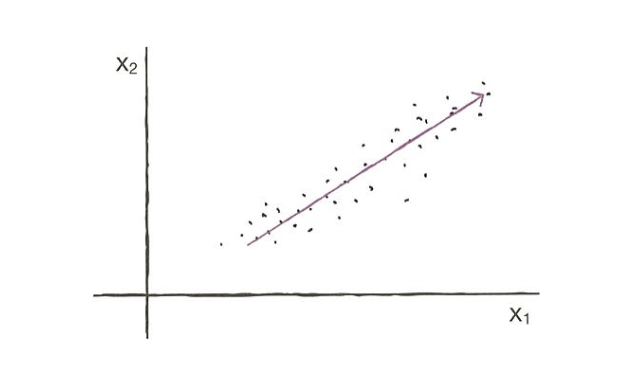
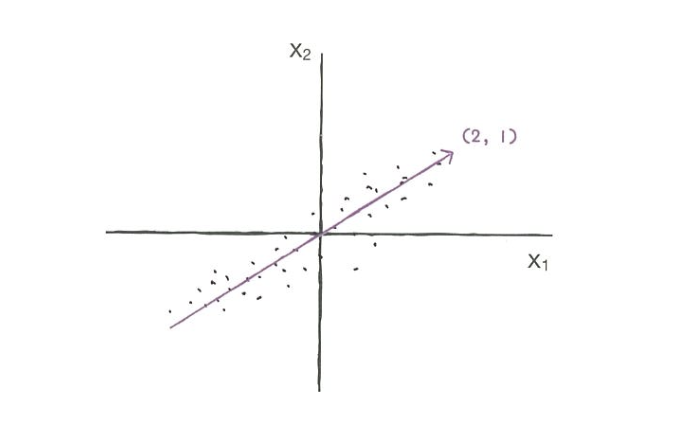
-
이 벡터를 주성분 이라고 부름
-
주성분 벡터의 원소 개수 = 원본 데이터셋에 있는 특성 개수
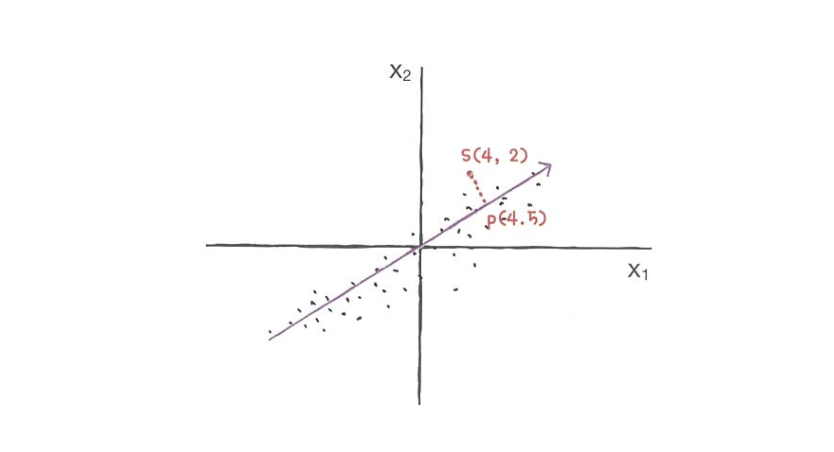
- ex) 샘플 데이터 s(4,2)를 주성분에 직각으로 투영 -> p(4.5) 만들 수 있다.
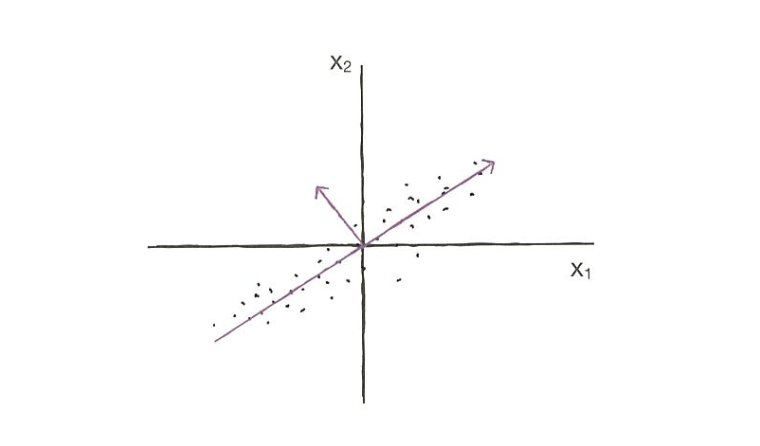
- 첫 번째 주성분 벡터에 수직이고 분산이 가장 큰 다음 방향을 찾음 -> 두 번째 주성분
PCA 클래스
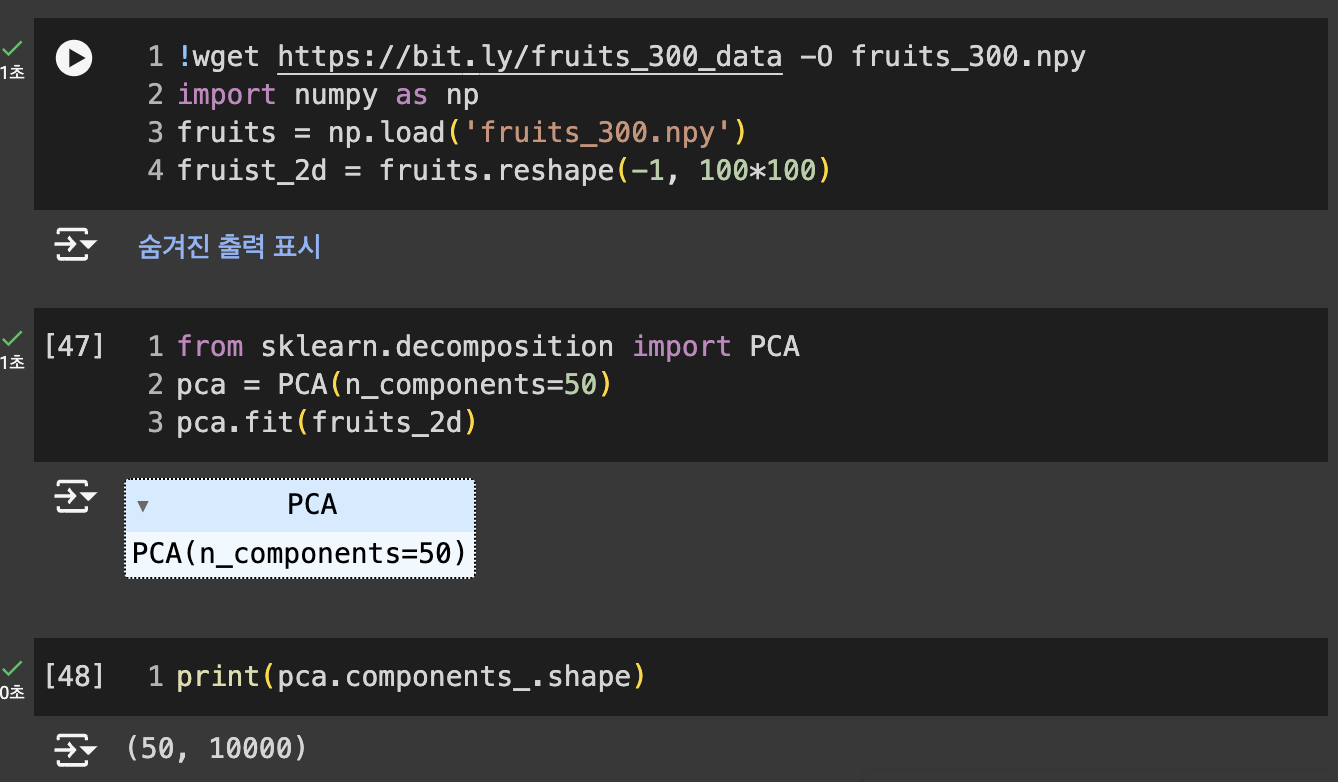
- PCA : 주성분 분석 알고리즘 제공
- n_components : 주성분 개수 지정
- components : PCA가 찾은 주성분 저장
결과
n_components=50으로 지정했기 때문에 50개의 주성분을 찾음. -> 첫 번째 차원 = 50, 두 번째 차원 = 원본 데이터의 특성 개수인 10,000

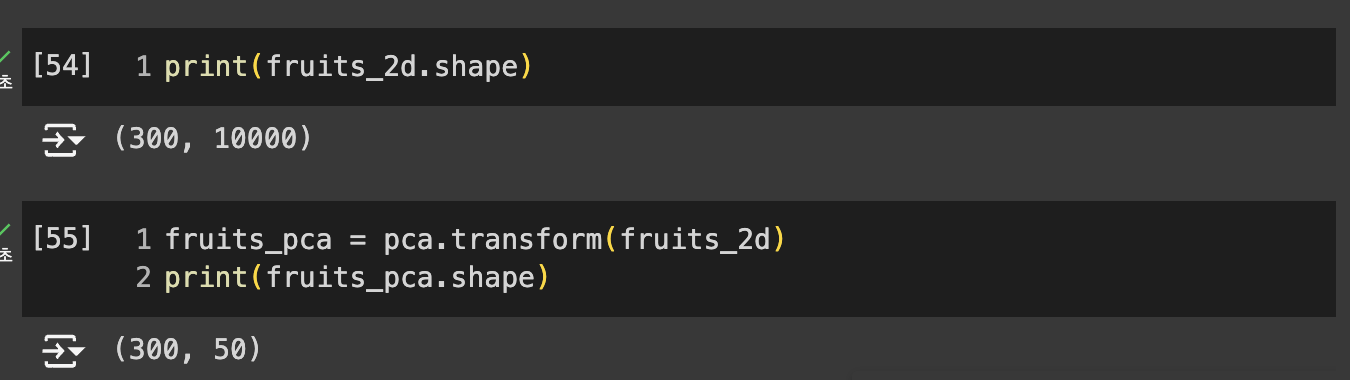
fruits_2d는 (300,10000) 크기의 배열 => (300, 50) 크기의 배열로 변환
원본 데이터 재구성

- inverse_transform() : 복원하는 메서드



설명된 분산
: 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값
- explainedvariance_ratio 에 분산 비율 기록

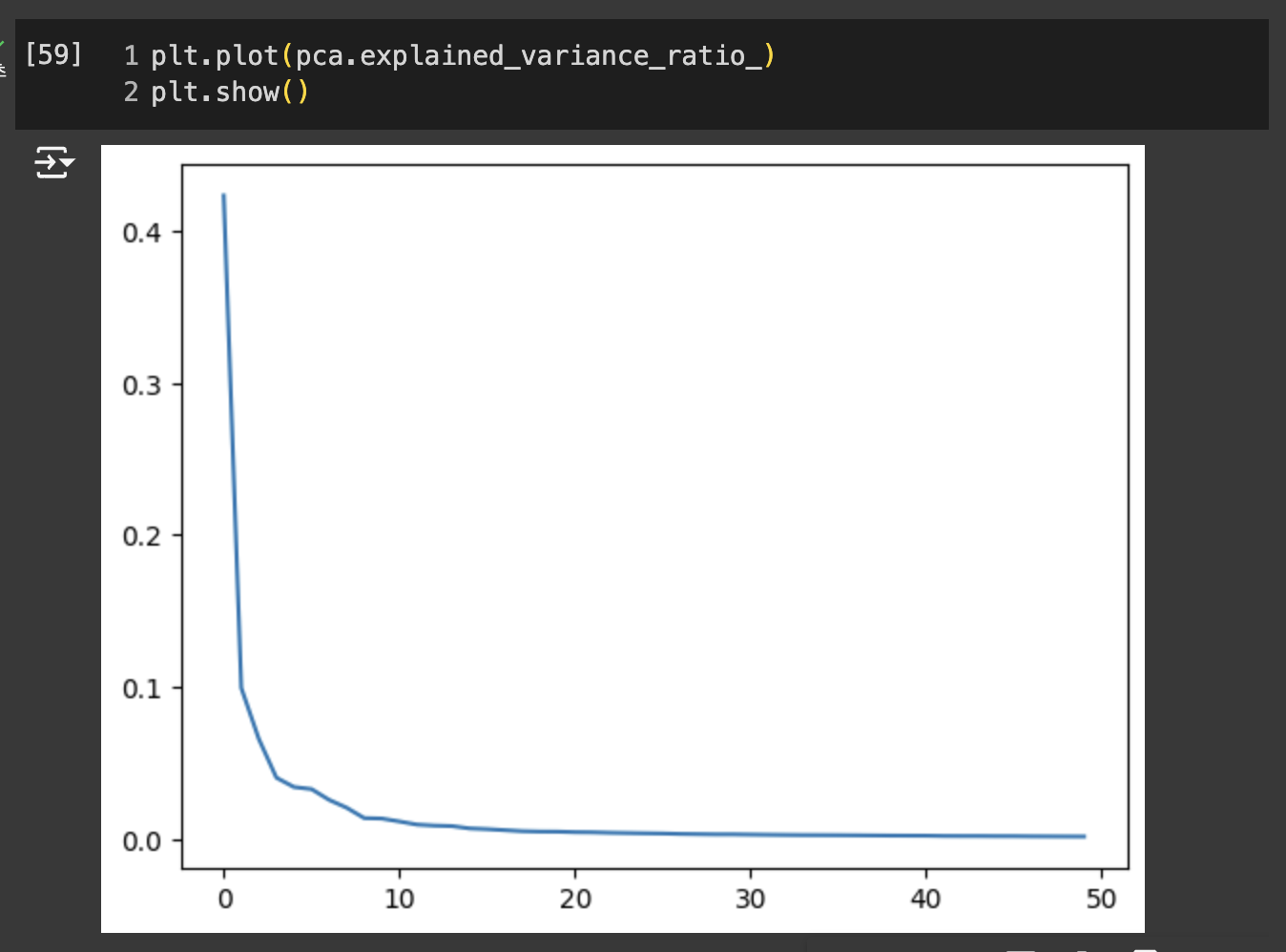
- 처음 10개의 주성분ㄴ이 대부분의 분산을 표현하고 있다.
다른 알고리즘과 함께 사용하기
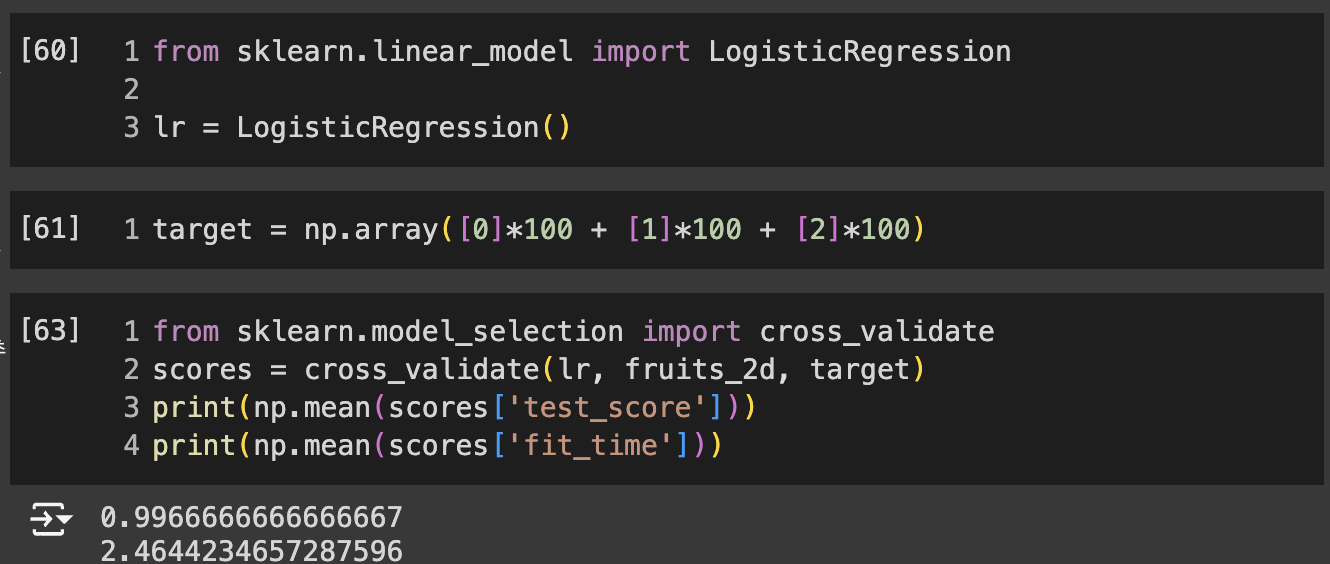

- pca 사용한 것이 정확도, 훈련 시간이 더 좋음
- 차원을 축소하면 저장공간 뿐만 아니라 머신러닝 모델의 훈련 속도도 높일 수 있다.
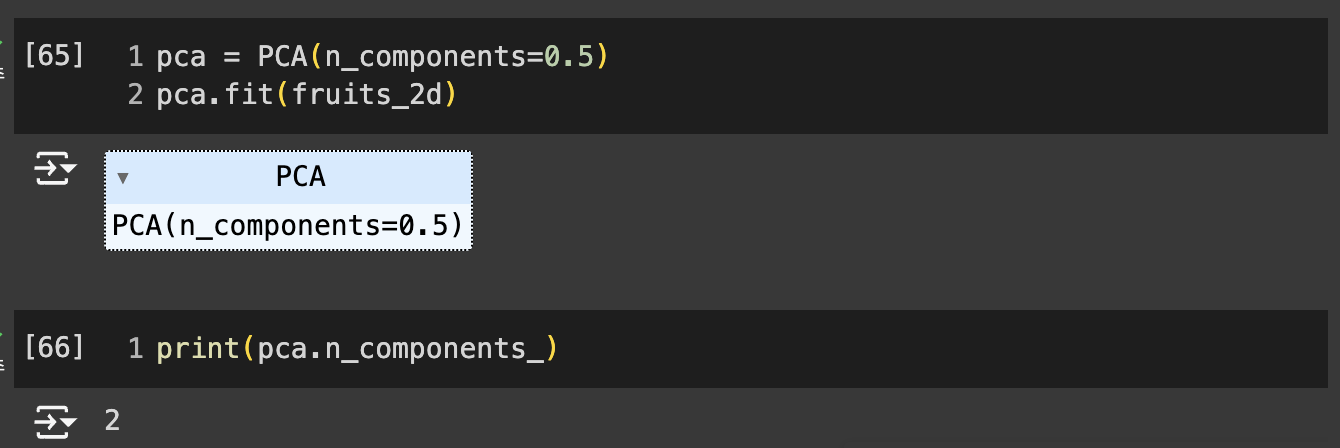
- n_components : 분산의 비율 지정 가능
- 지정된 비율에 도달할 때까지 자동으로 주성분 찾음
-> 2개의 특성만으로 원본 데이터에 있는 분산의 50% 표현 가능

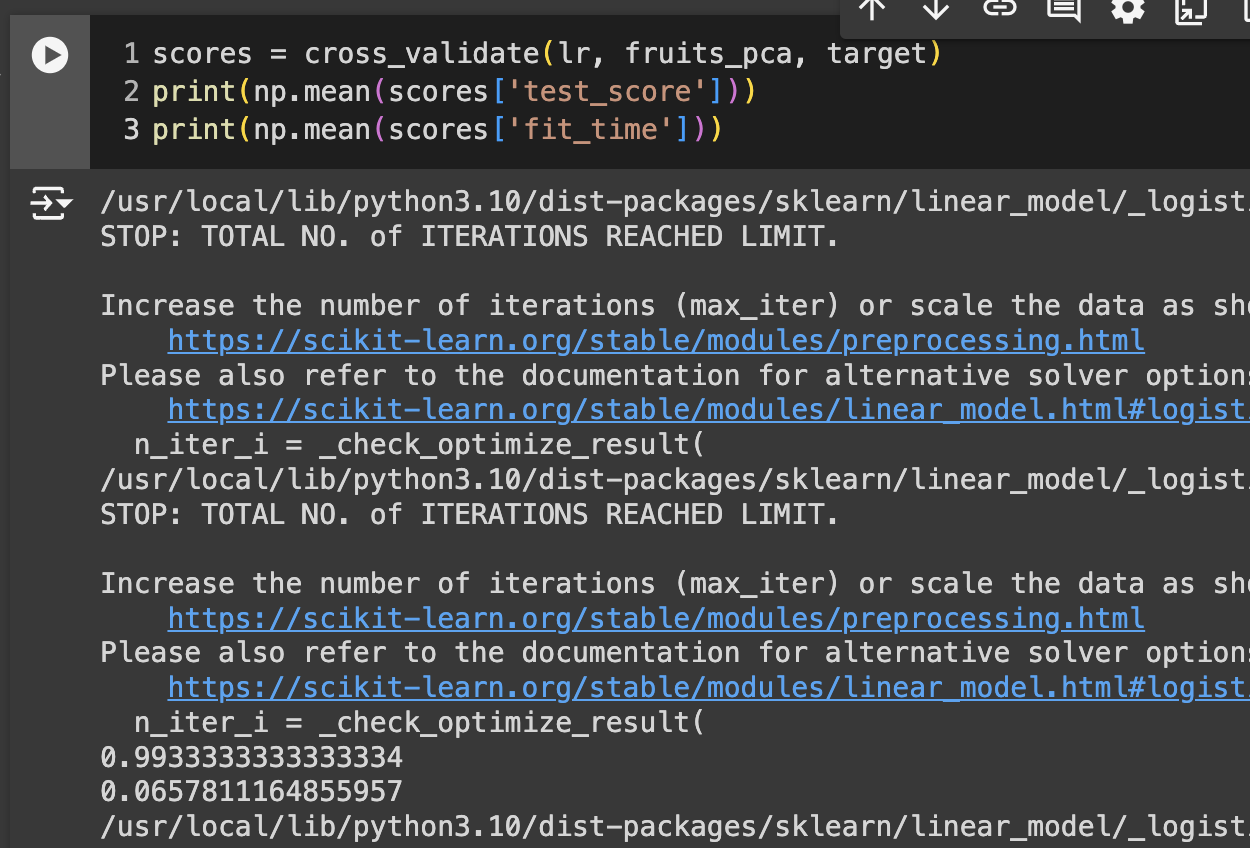
99% 정도의 정확도 달성





훈련 데이터의 차원을 줄이면 얻을 수 있는 또 하나의 장점 = 시각화
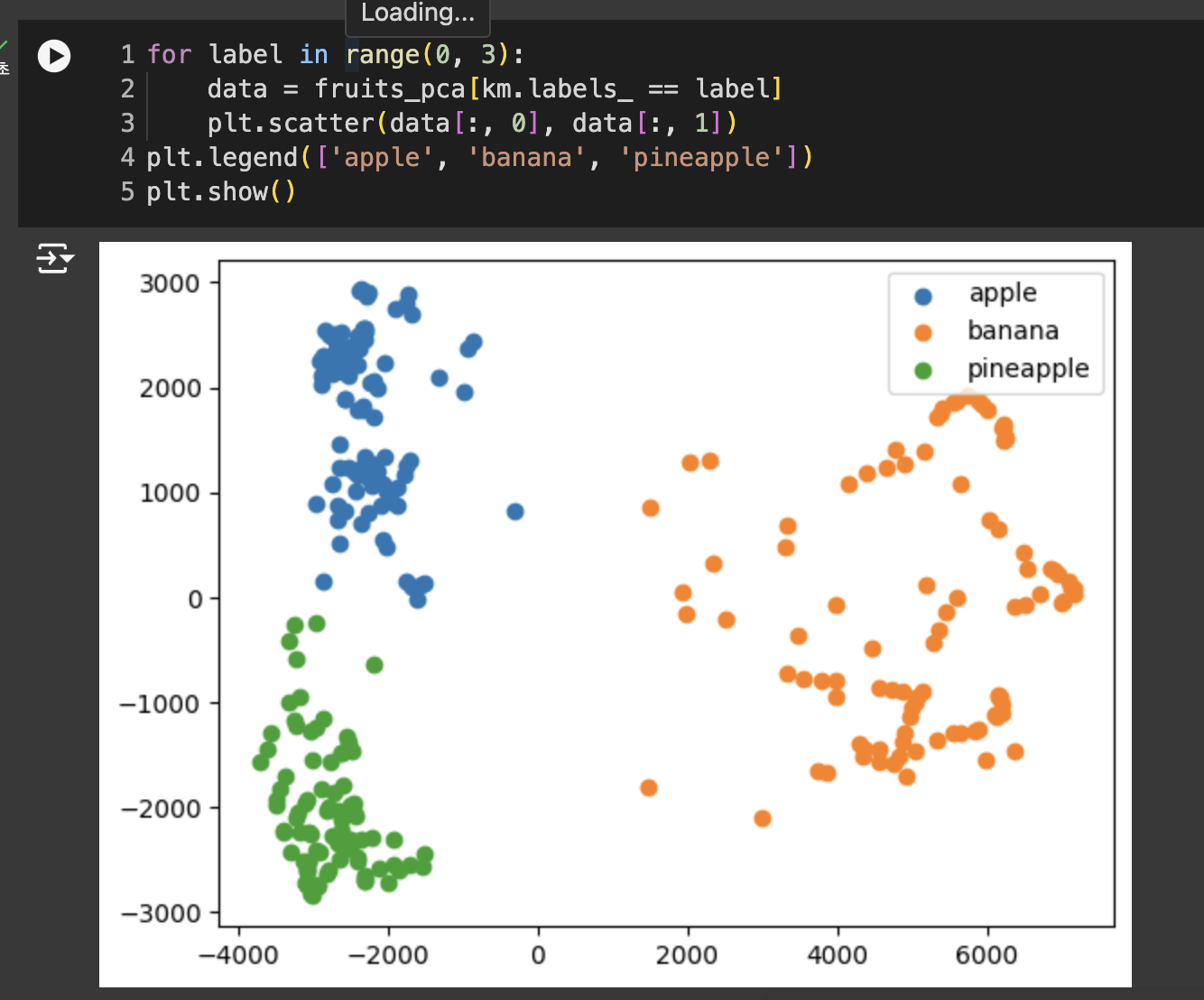

3번 풀이
주성분 분석은 가장 분산이 큰 방향부터 차례대로 수평으로 가면서 찾음. 따라서 첫 번째 주성분이 설명된 분산이 가장 크다.
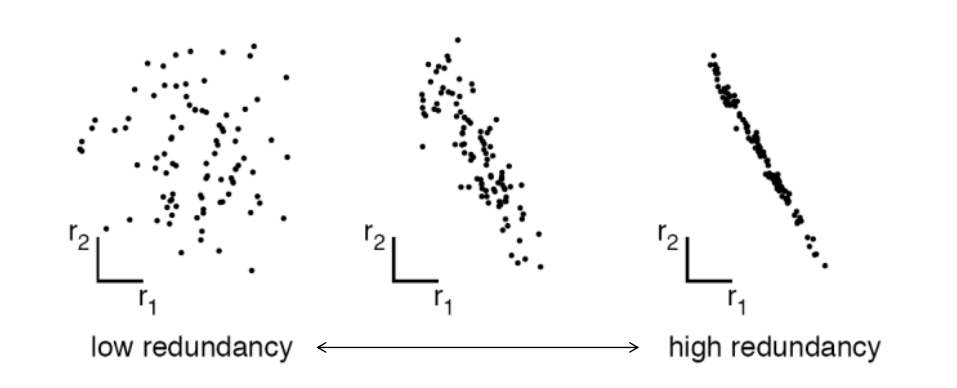
헷갈려서 다시 공부하는 주성분 분석(PCA)
주성분 분석(Principal Component Analysis, PCA)는 여러 개의 독립변수들을 가장 잘 설명해줄 수 있는 주된 성분을 추출하는 기법
핵심 특성만 선별하기 때문에 독립 변수의 수(차원)를 줄일 수 있음. 여러 개의 변수들이 소수의 특정한 변수들로 축약되도록 가공하는 것
흔히 말하는 차원의 저주를 방지하기 위한 것
차원의 저주(Curse of dimensionality)란?
데이터 차원이 증가할수록 해당 공간의 크기가 기하급수적으로 증가하며, 데이터 분석이나 모델 학습에 어려움을 초래하는 현상
차원 축소 시, 데이터의 일부 정보 손실 발생 가능. 어떤 차원을 유지하고 제거할지 결정하는 것이 복잡할 수 있음
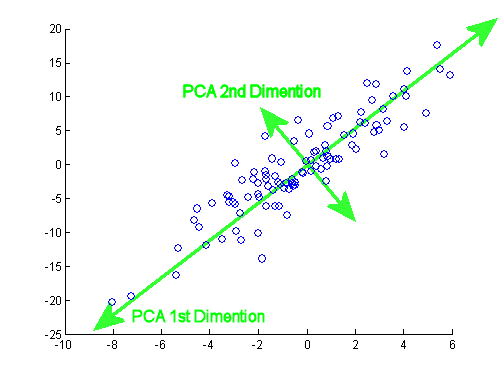
PCA 수행 시 데이터의 구조를 가장 잘 반영하는 기저를 찾는 것이 중요 -> 최적의 기저(Optimal Bases)라고 부름
PCA에서는 자동으로 분산이 최대가 되는 방향으로 최적의 기저를 찾아냄
