💡 목표 : Chapter01~02 + 코랩 실습 화면 캡쳐 + Ch.02(02-1) 확인 문제 풀고, 풀이 과정 정리하기

서론

혼공학습단 12기에 선정되어 혼공머신 책으로 스터디를 진행하게 되었다. 나는 당첨 운이 하나도 없는데, 이렇게 학습단에 선정되어 공부할 수 있는 기회가 주어졌다는 것이 너무 기뻤다. 그래서 열심히 공부해보려고 했는데, 역시 나는 미루기를 좋아하는 특성을 버릴 수 없었다… 다음 주부터는 미루지 않고 하고 싶다… 이번에 선택한 책은 머신러닝과 딥러닝에 관한 것인데 항상 배우고 싶지만 끝까지 해내지 못했던 주제라 선정하게 되었다. 애매하게 아는 지식을 버리고 처음부터 제대로 공부해보고싶다.

인공지능

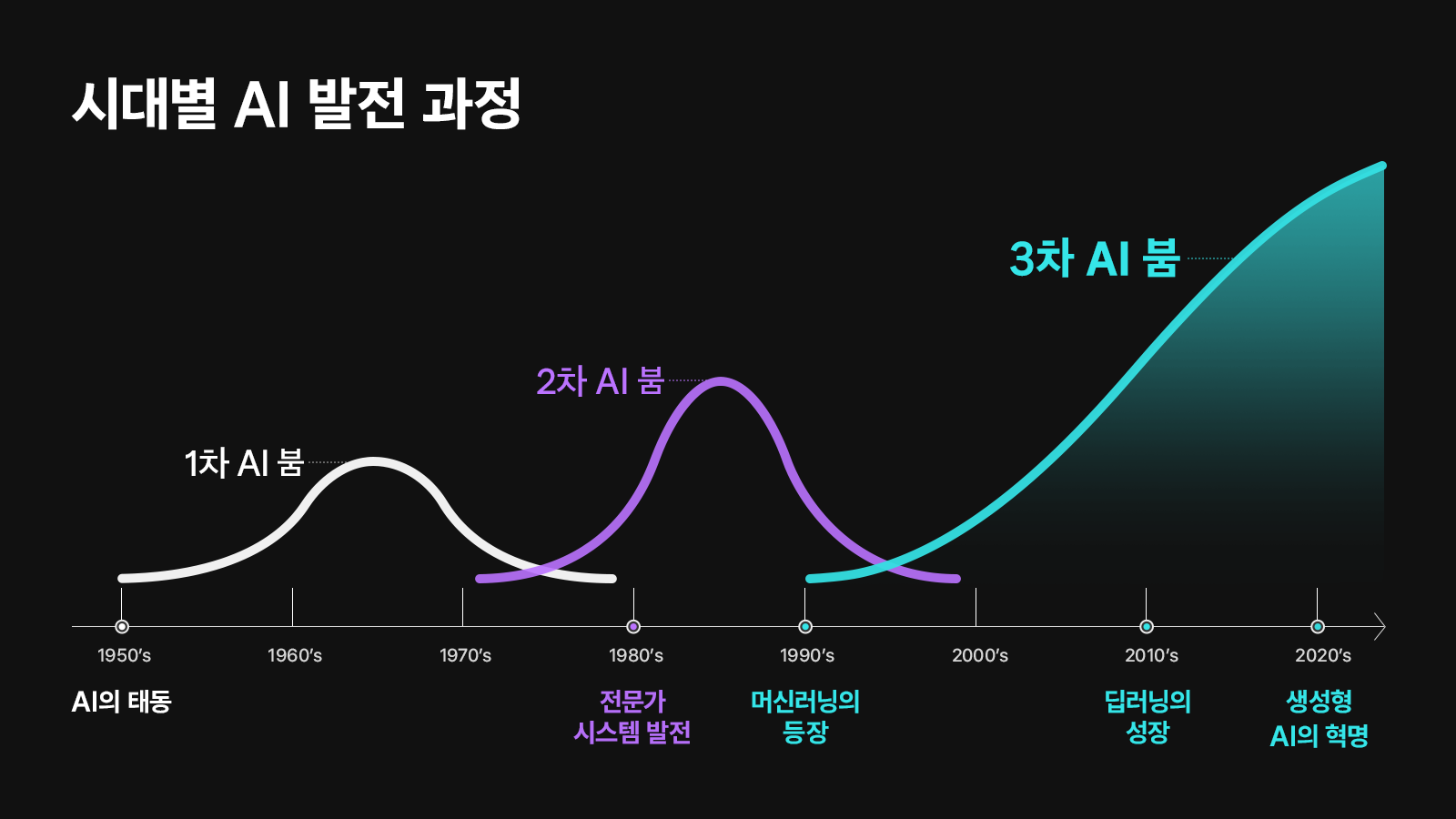
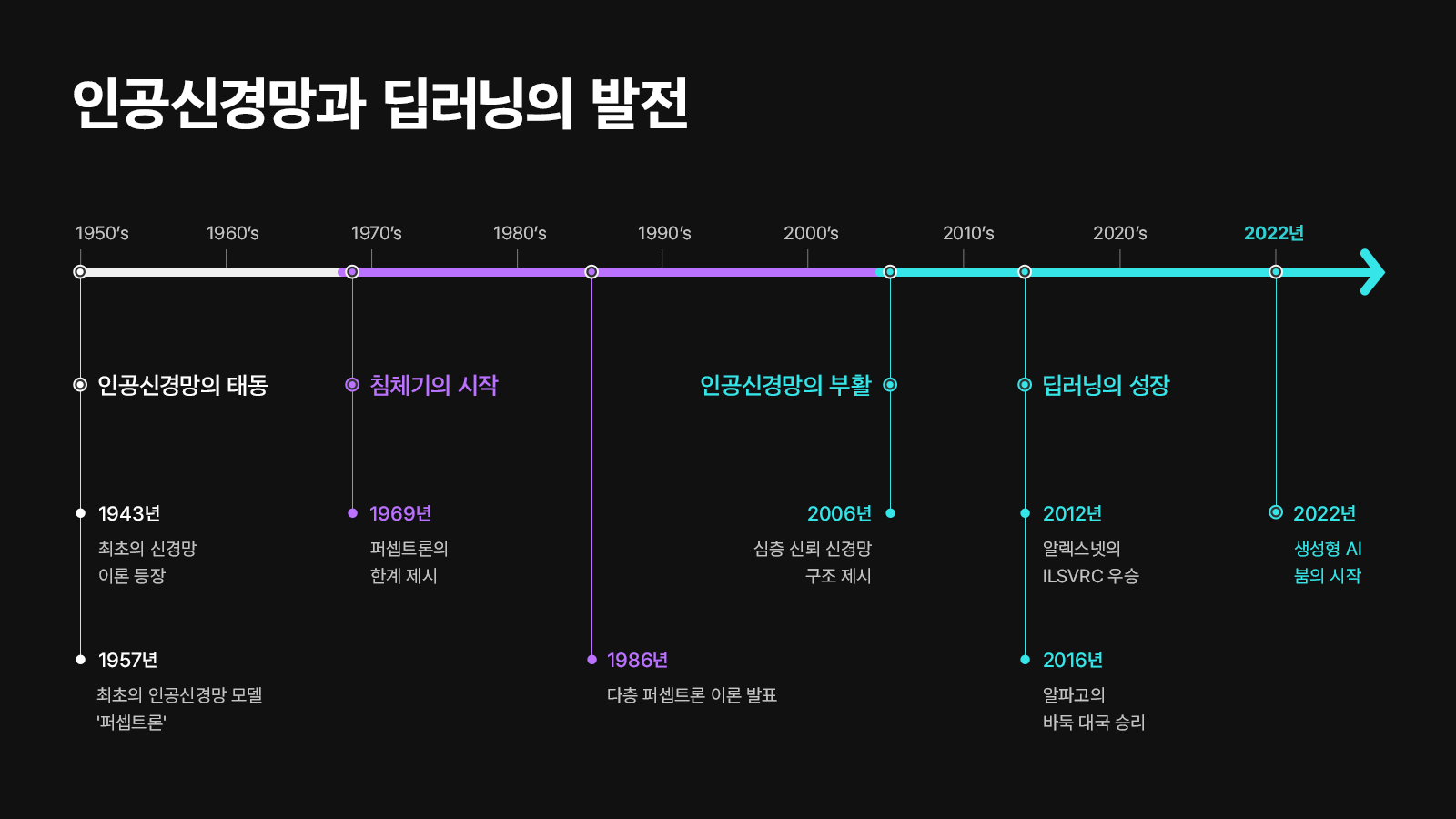출처 : SK 하이닉스 (https://news.skhynix.co.kr/post/all-around-ai-1))

인공지능(AI, Artificial Intelligence)

인공지능은 사람처럼 학습하고 추론할 수 있는 지능을 가진 컴퓨터 시스템을 만드는 기술이다.

1943년 워런 매컬러와 윌터 피츠가 최초로 뇌의 뉴런 개념을 발표했다.

1950년 앨런 튜링이 그 유명한 튜링 테스트를 발표한다. 튜링 테스트는 5분간 대화를 나눈 후 컴퓨터 프로그램과 의사소통이 가능한지, 사람과 같은 지능을 가졌는지 테스트하는 것이다.

1956년 다트머스 AI 컨퍼런스에서는 인공지능에 대한 전망이 최고조에 도달했다.

이 시기를 인공지능 태동기라고 한다.

그 이후 인공지능 황금기가 도래했다.

1957년 프랑크 로젠블라트가 로지스틱 회귀의 초기 버전으로 볼 수 있는 퍼셉트론을 발표했다.

1959년 데이비드 허블과 토르스텐 비셀이 고양이를 사용해 시각 피질에 있는 뉴런 기능을 연구했다.

하지만 컴퓨터 성능의 한계로 인해 첫 번째 AI 겨울이 도래했다.

그 다음 전문가 시스템이 등장해서 두 번째 AI 붐이 불었지만, 역시 한계를 드러내고 두 번째 AI 겨울을 맞이한다.

그 이후 머신러닝의 등장과 눈에 띄는 딥러닝의 성장에 의해 3차 AI 붐이 일어나고 있다.

머신러닝(ML, Machine Learning)

머신러닝은 규칙을 일일이 프로그래밍하지 않아도 자동으로 데이터에서 규칙을 학습하는 알고리즘을 연구하는 분야이다. 즉, 알고리즘을 이용하여 데이터를 분석하고, 분석 결과를 스스로 학습한 후, 이를 기반으로 어떠한 판단이나 예측을 하는 것을 의미한다.

출처 : 모두의 연구소(https://modulabs.co.kr/blog/machine-learning/)

대표적인 머신러닝 라이브러리에는 사이킷런(scikit-learn)이 있다.

딥러닝(Deep Learning)

머신러닝 알고리즘 중 인공 신경망(Aritificial Neural Network)을 기반으로 한 방법들을 통칭하여 딥러닝이라고 한다. 인공신경망과 딥러닝을 크게 구분하지 않고 사용하기도 한다.

1998년 얀 르쿤이 신경망 모델을 만들어 손글씨 숫자를 인식하는데 성공하고, 이 신경망의 이름을 LeNet-5라고 하였다. 이것이 최초의 합성곱 신경망이다.

2012년 제프리 힌턴이 이미지 분류 대회에서 합성곱 신경망을 사용한 AlexNet 모델을 이용하여 압도적인 성능으로 우승했다. 이때부터 이미지 분류 작업에 합성곱 신경망이 널리 사용되기 시작했다고 한다.

성능이 크게 향상될 수 있던 이유 3가지

1. 풍부한 데이터
2. 컴퓨터 성능의 향상
3. 혁신적인 알고리즘 개발

딥러닝 라이브러리로는 텐서플로(TensorFlow)와 파이토치(PyTorch)가 있다.

공통점은 인공 신경망 알고리즘을 전문으로 다루고 있다는 것과 파이썬 API를 제공한다는 점이다.

학습 환경

머신러닝을 학습하기 위해서는 실습 환경이 필요하다. 이 책에서는 코랩에서의 실습 환경을 보여준다.

코랩(Colab)

이미 많이 써봤지만, 간단하게 정리를 다시 해보자.

• 코랩 파일 = 노트북
• 셀 = 코드 또는 텍스트의 덩어리, 코랩에서 실행할 수 있는 최소 단위.
  • 노트북은 여러 개의 코드 셀과 텍스트 셀로 이루어진다.
  • 텍스트 셀에서는 HTML과 마크다운을 혼용해서 사용 가능하다.
• 코랩 노트북은 가상 서버를 사용한다.
• 구글 클라우드의 컴퓨터 엔진과 연결되어 있고, 메모리는 약 12기가, 디스크 공간은 100기가이다.

CH01-2. 확인문제

01-3. 마켓과 머신러닝

목표

K-최근접 이웃을 사용하여 2개의 종류를 분류하는 머신러닝 모델 훈련해보기

배경

한빛 마켓에서 앱 마켓 최초로 살아 있는 생선을 판매하기 시작했다. 그런데 새로운 직원이 생선 이름을 도통 외우질 못한다. 그래서 생선 이름을 자동으로 알려주는 머신러닝을 만들려고 한다. 우선은 도미와 빙어를 구분해보자.

생성 분류 문제

생선의 분류는 생선의 특징을 알면 쉽게 구분이 가능할 것이다.

• 생선 길이가 30cm 이상이면 도미이다.

하지만 무조건 도미일 수는 없다.

머신러닝의 장점은 누구도 알려주지 않은 기준을 스스로 찾아 일을 한다는 것이다.

순서대로 모델을 훈련해보자.

1. 도미 데이터 준비하기

기준을 스스로 찾기 위해서는 풍부한 데이터가 필요하다.

https://gist.github.com/rickiepark/b37d04a95a42ef6757e4a99214d61697

이진 분류
머신러닝에서 여러 개의 종류(클래스) 중 하나를 구별해 내는 문제를 분류라고 한다. 특히 2개의 클래스 중 하나를 고르는 문제를 이진 분류라고 한다.

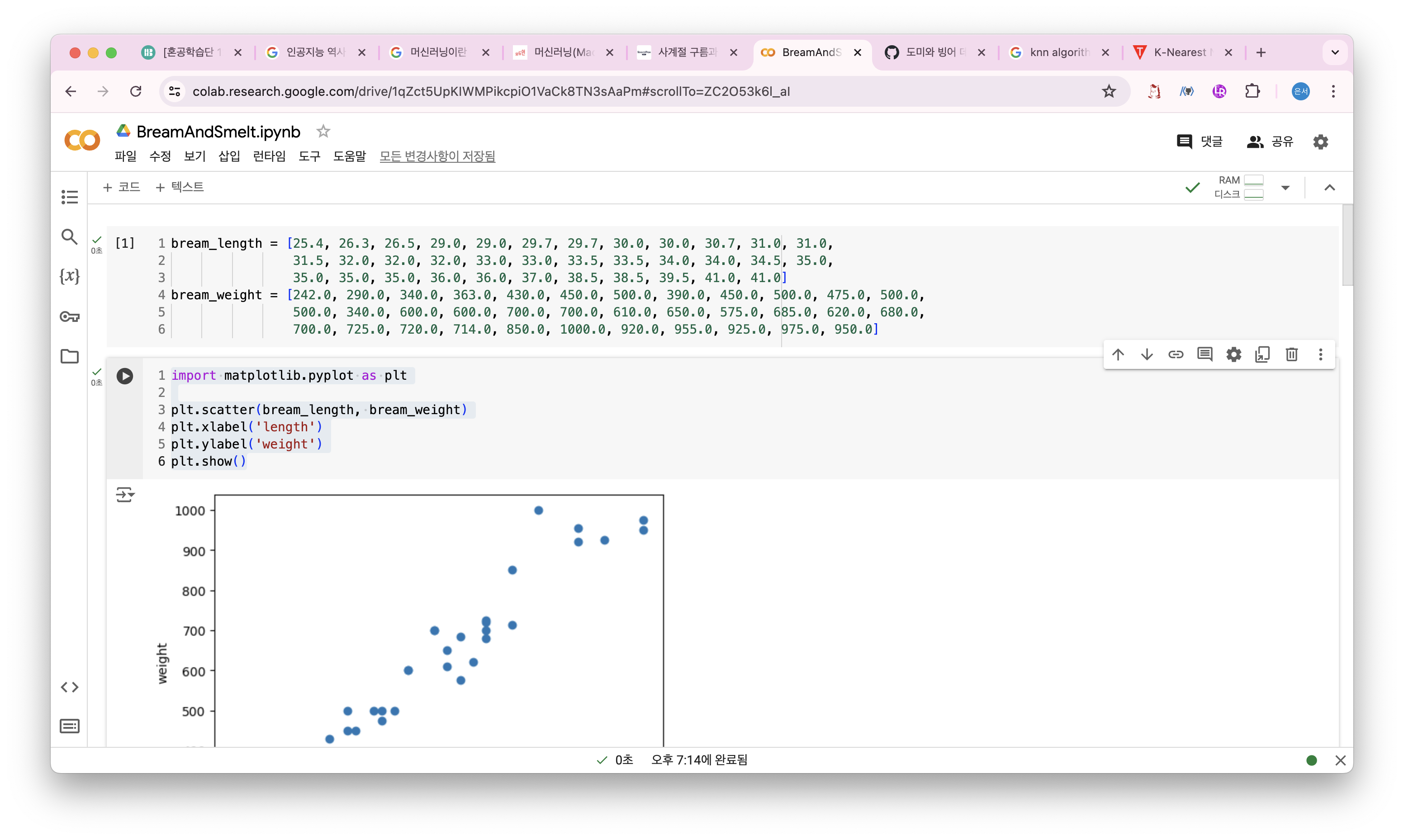
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]

리스트에서 첫 번째 도미의 길이는 25.4cm, 무게는 242.0g이다.

특징을 길이와 무게로 표현한 것이다. 이러한 특징을 특성(Feature)이라고 부른다.

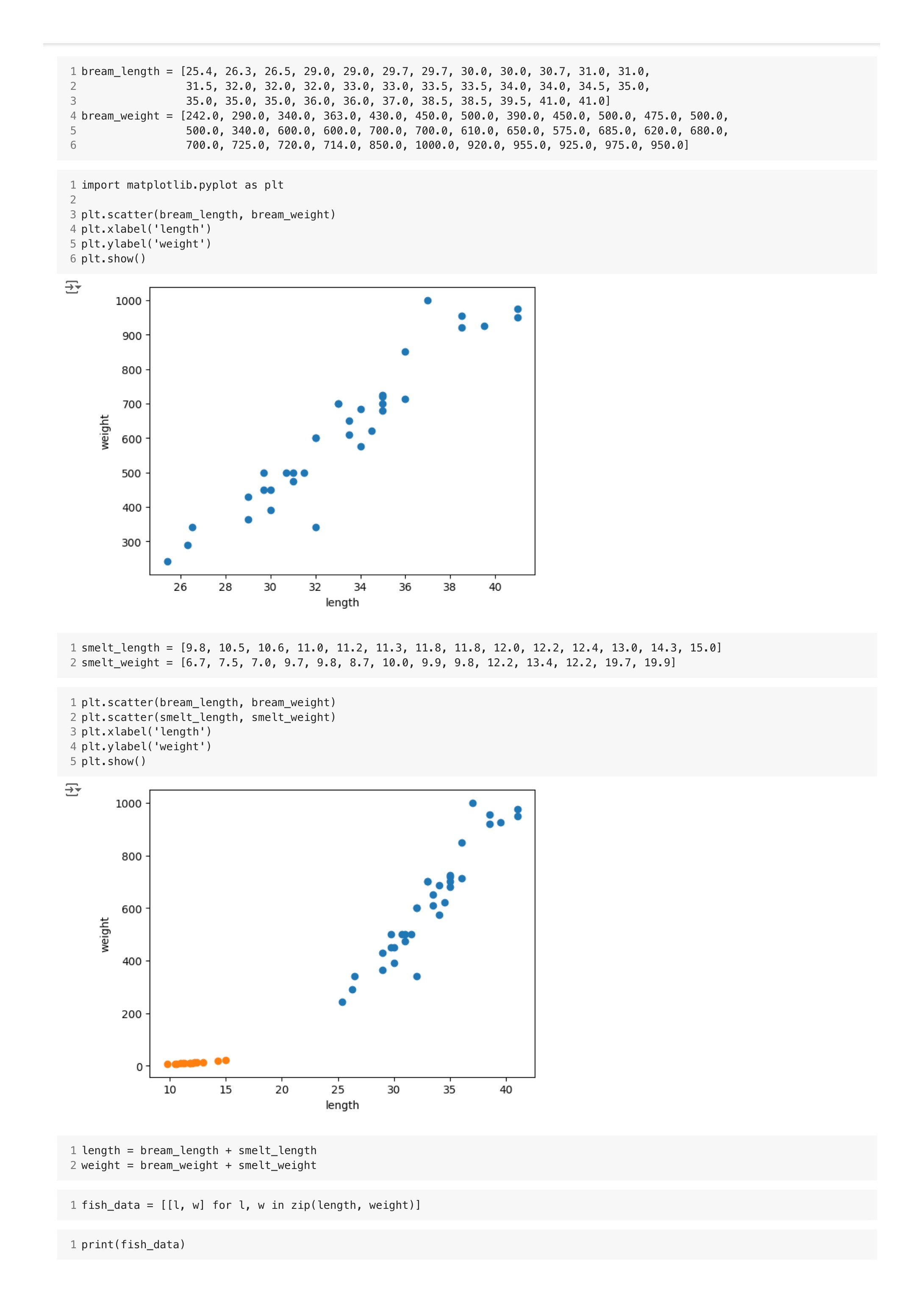
두 특성을 그래프로 표현하면 숫자로 보는 것보다 데이터를 잘 이해할 수 있다.

그래프에 점으로 표시 한 것을 산점도(Scatter plot)라고 부른다.

대표적인 패키지는 맷플롯립(matplotlib)이다.

import matplotlib.pyplot as plt

plt.scatter(bream_length, bream_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()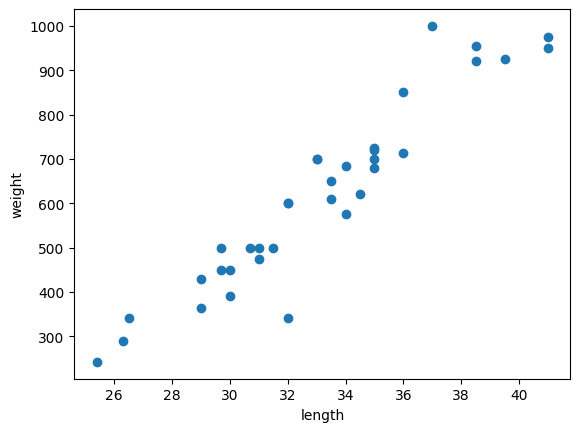

x축은 길이, y축은 무게이다. 2개의 특성을 사용했으므로 2차원 그래프이다.

그래프가 일직선에 가까운 형태로 나타나는 경우를 선형적이라고 한다.

2. 방어 데이터 준비하기

https://gist.github.com/rickiepark/1e89fe2a9d4ad92bc9f073163c9a37a7

smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

마찬가지로 산점도로 그래프를 그려보면 다음과 같다.

plt.scatter(bream_length, bream_weight)
plt.scatter(smelt_length, smelt_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()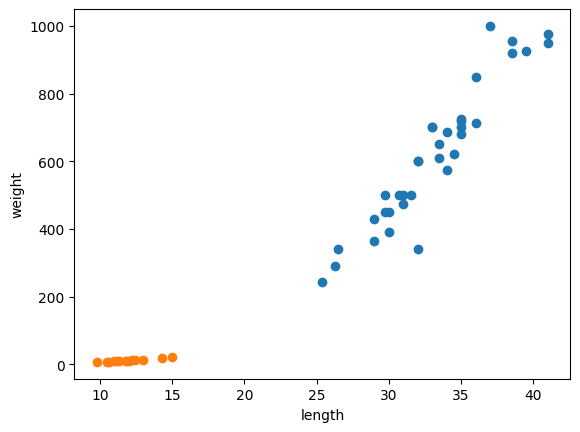

색으로 구분해서 나타낸 것이다. 주황색이 빙어이고, 파란색이 도미이다.

3. 첫 번째 머신러닝 프로그래밍

K-최근접 이웃 알고리즘을 사용해보자.

length = bream_length + smelt_length
weight = bream_weight + smelt_weight

두 리스트를 하나로 합쳤다.

머신러닝 패키지인 사이킷런을 사용하려면 세로 방향으로 늘어뜨린 2차원 리스트가 필요하다.

따라서 zip( ) 함수와 리스트 내포 구문을 사용해서 만들어 보자.

fish_data = [[l, w] for l, w in zip(length, weight)]

zip( )함수는 length, weight 리스트에서 원소를 하나씩 꺼내어 l, w에 할당하고, [l,w]가 하나의 원소로 구성된 리스트가 만들어진다.

print(fish_data)

이러한 리스트를 2차원 리스트 혹은 리스트의 리스트라고 부른다.

다음으로 준비할 데이터는 정답 데이터이다. 어떤 것이 어떤 생선인지 답을 만드는 것이다.

규칙을 찾기 위해서는 답을 알려줘야하기 때문이다.

fish_target = [1] * 35 + [0] * 14
print(fish_target)

이제 K-최근접 이웃 알고리즘을 구현한 클래스인 KNeighborsClassifier를 사용해보자.

from sklearn.neighbors import KNeighborsClassifier

kn = KNeighborsClassifier()

먼저 임포트한 클래스의 객체를 만든다.

이 객체에 fish_data, fish_target을 전달하여 도미를 찾을 수 있는 기준을 학습시킬 것이다.

이러한 과정을 훈련(Training)이라고 한다. 사이킷런에서는 fit( )메서드가 이런 역할을 한다.

fit( )으로 데이터 알고리즘을 훈련하고, score( ) 메서드로 모델이 얼마나 잘 훈련되었는지 평가한다.

0~1 사이의 값을 반환하고, 정확할 수록 1에 가까워진다.

kn.fit(fish_data, fish_target)
kn.score(fish_data, fish_target)

이 값을 정확도(accuracy)라고 한다.

K-최근접 이웃 알고리즘

이 알고리즘은 주위의 다른 데이터를 보고 다수를 차지하는 것을 정답으로 사용한다.

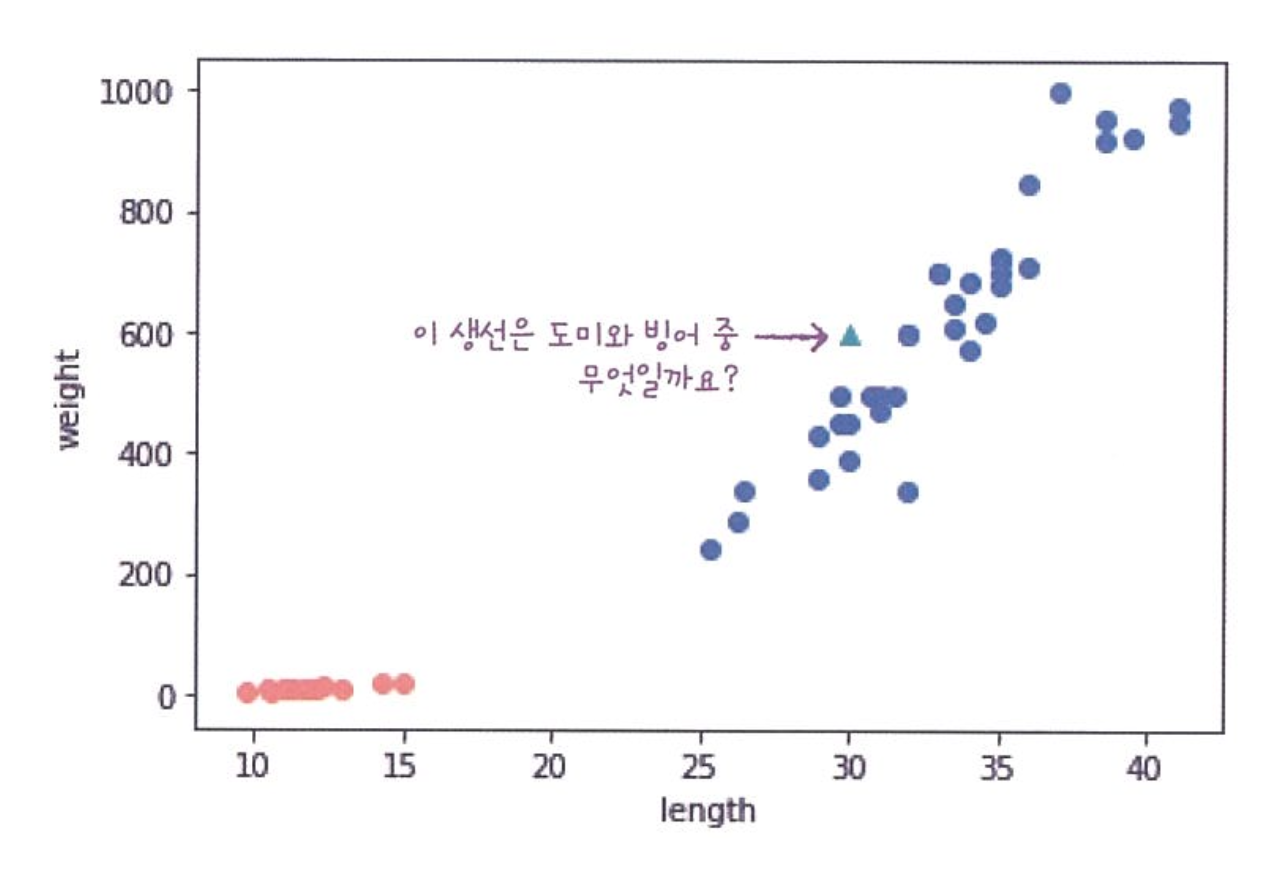
이렇게 있을 때 이 삼각형 주변에 다른 도미 데이터가 많기 때문에 도미라고 판단할 것이다. 실제로 코드로 확인해보면 1로 예측한다.

kn.predict([[30,600]])

새로운 데이터에 대해 예측할 때는 가장 가까운 직선거리에 어떤 데이터가 있는지 살피면 된다.

다만, 데이터가 아주 많은 경우 사용하기 어렵다.

KNeighborsClassifier 클래스의 _fit_X 속성에는 fish_data를 _y 속성에는 fish_target을 가지고 있다.

print(kn._fit_X)

print(kn._y)

가까운 데이터 중 몇 개를 참고할 지는 n_neighbors 매개변수로 바꿀 수 있다.

만약 이웃의 수를 49개로 한다면? 49개 중 도미가 35개이므로 어떤 값을 넣어도 도미로 예측할 것이다.

kn49 = KNeighborsClassifier(n_neighbors=49)
kn49.fit(fish_data, fish_target)
kn49.score(fish_data, fish_target)

print(35/49)

도미만 맞췄으니 35/49한 값과 동일한 값이 나온다.

01-3. 확인 문제

02-1. 훈련 세트와 테스트 세트

목표

지도 학습과 비지도 학습의 차이를 배운다.

훈련 세트와 테스트 세트로 데이터를 나누어 학습한다.

배경

당연히 정답을 다 줬는데 못맞추는게 이상하지 않을까?

지도 학습과 비지도 학습

머신러닝 알고리즘은 지도학습과 비지도학습으로 나눌 수 있다.

지도학습은 훈련을 위한 데이터와 정답이 필요하다.

이 데이터를 입력, 정답을 타깃이라 부르고, 이 둘을 합쳐 훈련 데이터라고 부른다.

그리고 입력으로 사용된 길이와 무게를 특성이라고 했다.

지도 학습은 정답(타깃)이 있으니 알고리즘이 정답을 맞히는 것을 학습한다.

비지도 학습은 타깃 없이 입력 데이터만 사용해야하므로 맞힐 수가 없다. 대신 데이터를 파악하거나 변형하는데 도움을 준다.

훈련 세트와 테스트 세트

타깃을 주고 훈련한 다음, 같은 데이터로 테스트하면 모두 맞히는 것이 당연하다.

알고리즘의 성능을 제대로 평가하려면 훈련 데이터와 평가에 사용할 데이터가 각각 달라야 한다.

이를 위한 간단한 방법은 다른 데이터를 준비하거나 일부 떼어 내어 활용하는 것이며, 후자의 경우가 많다.

평가에 사용하는 데이터를 테스트 세트, 훈련에 사용하는 데이터를 훈련 세트라고 부른다.

1. 다시 데이터를 준비해보자.

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 
                10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 
                7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

2. 2차원 리스트로 바꾸자.

fish_data = [[l,w] for l,w in zip(fish_length, fish_weight)]
fish_target = [1]*35 + [0]*14

이때 하나의 생선 데이터를 샘플이라고 부른다. 여기서는 총 49개의 샘플이 있는 것이다.

우선, 앞의 35개를 훈련 세트로, 나머지 14개를 테스트 세트로 사용해보자.

3. 객체 만들기

from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()

4. 데이터 나누기

인덱스와 슬라이싱을 사용하여 지정할 수 있다.

• 슬라이싱의 경우 마지막 인덱스의 원소는 포함되지 않는다.

train_input = fish_data[:35]
train_target = fish_target[:35]
test_input = fish_data[35:]
test_target = fish_target[35:]

5. 훈련 세트로 모델 훈련, 테스트 세트로 평가

kn = kn.fit(train_input, train_target)
kn.score(test_input, test_target)

정확도가 0이 나온다.

당연하다… 도미 데이터로 훈련시켜놓고 빙어 데이터로 테스트 하면 정확도가 나오겠냐고…

샘플링 편향

훈련 세트와 테스트 세트로 나누려면 데이터가 골고루 섞여야 한다. 이렇게 샘플이 골고루 섞여 있지 않으면 샘플링이 한 쪽으로 치우쳤다는 의미로 샘플링 편향이라고 부른다.

6. 데이터를 넘파이 배열로 변환

import numpy as np

input_arr = np.array(fish_data)
target_arr = np.array(fish_target)

print(input_arr)

print(input_arr.shape)

샘플 수와 특성 수가 각각 49, 2개인 것을 확인할 수 있다.

이제 이 배열에서 랜덤하게 샘플을 선택해 훈련 세트와 테스트 세트를 만들면 된다.

np.random.seed(42)
index = np.arange(49)
np.random.shuffle(index)

arange( ) 함수에 정수 N을 전달하면 0에서부터 N-1까지 1씩 증가하는 배열을 만든다.

shuffle( ) 함수는 주어진 배열을 무작위로 섞는다.

print(index)

train_input = input_arr[index[:35]]
train_target = target_arr[index[:35]]

print(input_arr[13], train_input[0])

나머지 14개도 테스트 세트로 만들자.

test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]

잘 섞였는지 산점도로 확인해보자.

import matplotlib.pyplot as plt
plt.scatter(train_input[:, 0], train_input[:,1])
plt.scatter(test_input[:, 0], test_input[:,1])
plt.xlabel('length')
plt.ylabel('weight')
plt.show()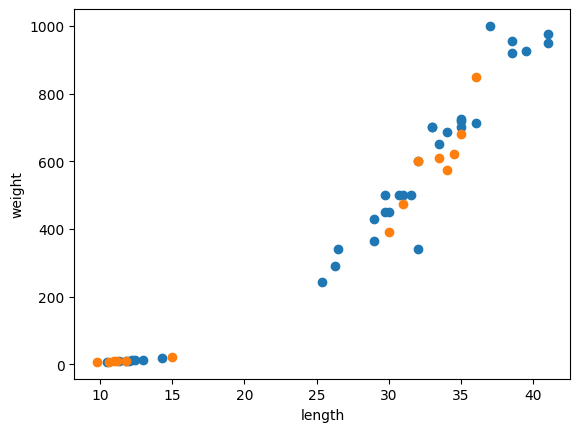

데이터가 준비되었으므로 모델을 다시 학습시켜보자.

kn = kn.fit(train_input, train_target)
kn.score(test_input, test_target)

kn.predict(test_input)

test_target

테스트 세트에 대한 예측 결과가 정답과 일치한 것을 볼 수 있다.

02-1. 확인 문제

02-2. 데이터 전처리

목표

데이터 전처리 과정을 거치고, 표준 점수로 특성의 스케일을 변환해본다.

배경

길이가 25cm, 무게가 150g인 도미인데 빙어로 예측이 된다. 무슨 문제일까?

1. 넘파이로 데이터 준비하기

fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, 
                31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0, 
                35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8, 
                10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, 
                500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0, 
                700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7, 
                7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]

import numpy as np

fish_data = np.column_stack((fish_length, fish_weight))

print(fish_data[:5])

np.concatenate() 함수를 사용하여 병렬로 합칠 수 있다.

np.ones(), np.zeros() 는 각각 원하는 개수의 1과 0을 채운 배열을 만들어 준다.

fish_target = np.concatenate((np.ones(35), np.zeros(14)))

print(fish_target)

2. 훈련 세트와 테스트 세트 나누기

train_test_split( )함수를 이용해서도 나눌 수 있다. 나누기 전에 알아서 섞어 주기도 한다.

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, random_state=42)

print(train_input.shape, test_input.shape)

이 함수는 기본적으로 25%를 테스트 세트로 떼어 낸다.

print(test_target)

잘 섞인 것 같지만 두 생선의 비율은 2.5:1인데 여기서는 3.3:1로 나온다. 샘플링 편향이 여기서도 조금 나타나고 있는 것이다.

이렇게 무작위로 나누면 샘플이 골고루 섞이지 않을 수 있다. 특히, 클래스의 개수가 적을 때 이런 일이 생길 수 있다.

이때 stratify 매개변수에 타깃 데이터를 전달하면 클래스 비율에 맞게 데이터를 나눠준다.

train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, stratify=fish_target, random_state=42)

print(test_target)

3. 모델 훈련, 평가

from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn.fit(train_input, train_target)
kn.score(test_input, test_target)

print(kn.predict([[25, 150]]))

정확도는 1이 나오지만 여전히 도미로 예측을 못하고 있다.

산점도로 확인해보자

import matplotlib.pyplot as plt
plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()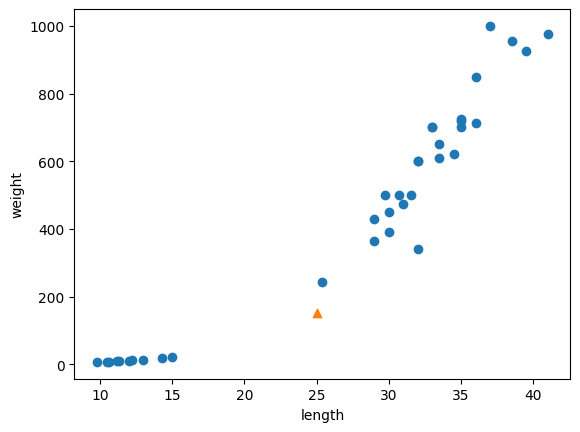

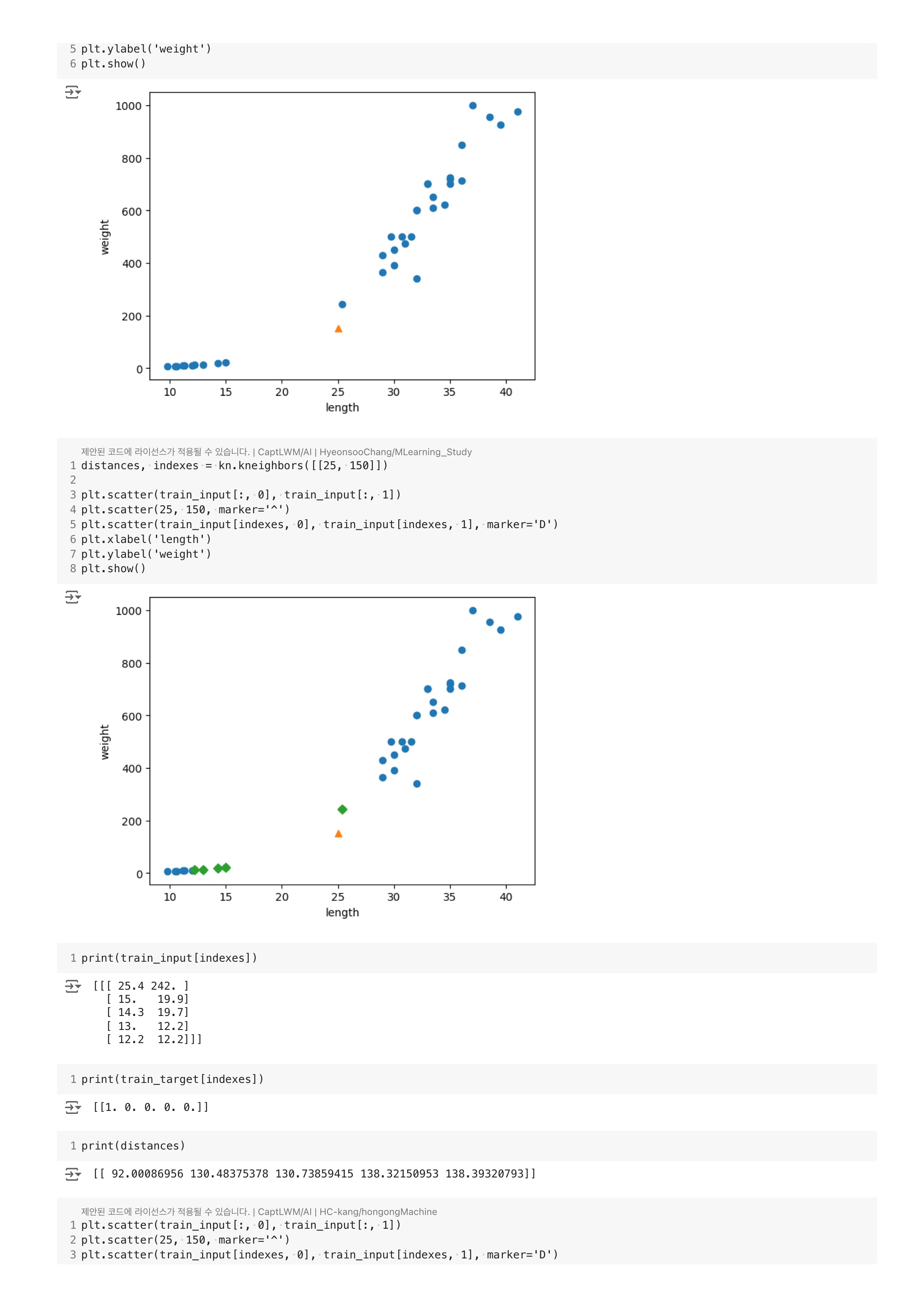
도미 데이터에 더 가까운데도 빙어 라고 판단한 이유가 뭘까?

가까운 이웃을 확인해보자.

distances, indexes = kn.kneighbors([[25, 150]])

plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes, 0], train_input[indexes, 1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()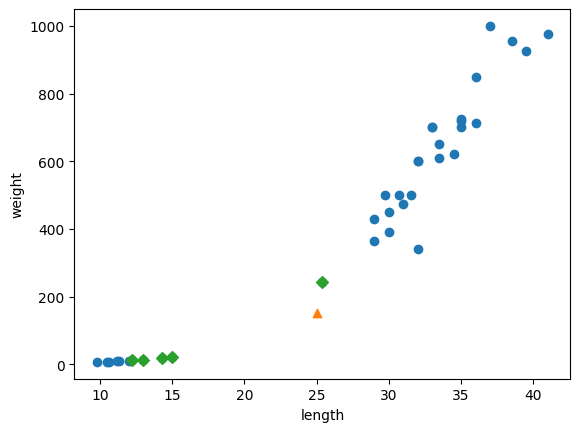

print(train_input[indexes])

print(train_target[indexes])

그래프와 실제 값을 확인해도 가까운 이웃으로 선정된 것이 빙어인 것을 확인할 수 있다.

이웃 샘플까지의 거리를 확인해보자.

print(distances)

기준

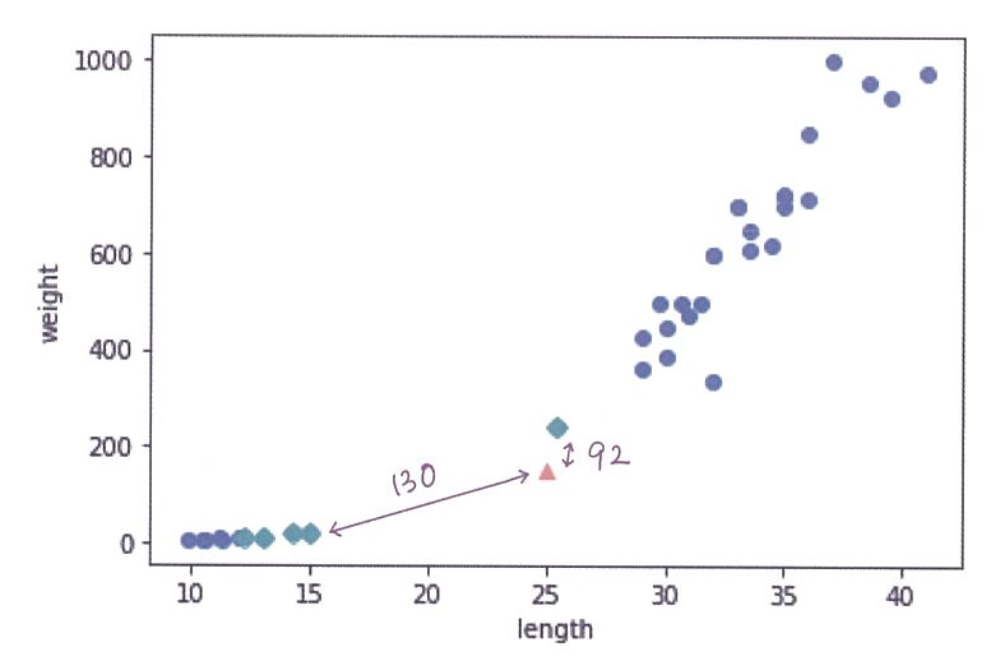
거리가 92와 130이라고 하기엔 비율이 이상하다.

그 이유는 x축이 범위가 10~40으로 좁고, y축은 0~1000으로 넓어서 그렇다.

따라서 x 축 범위를 xlim( ) 함수를 사용하여 맞춰보자.

plt.scatter(train_input[:, 0], train_input[:, 1])
plt.scatter(25, 150, marker='^')
plt.scatter(train_input[indexes, 0], train_input[indexes, 1], marker='D')
plt.xlim((0, 1000))
plt.xlabel('length')
plt.ylabel('weight')
plt.show()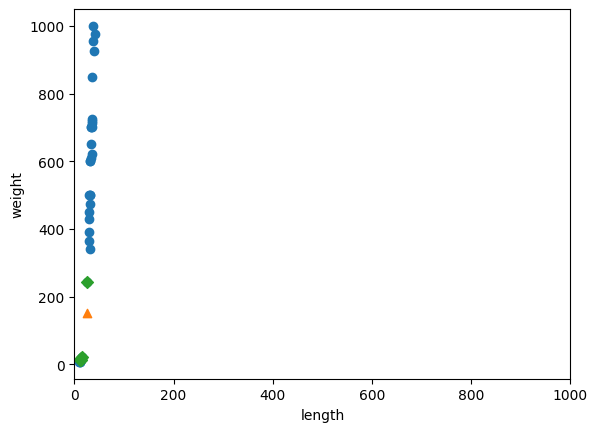

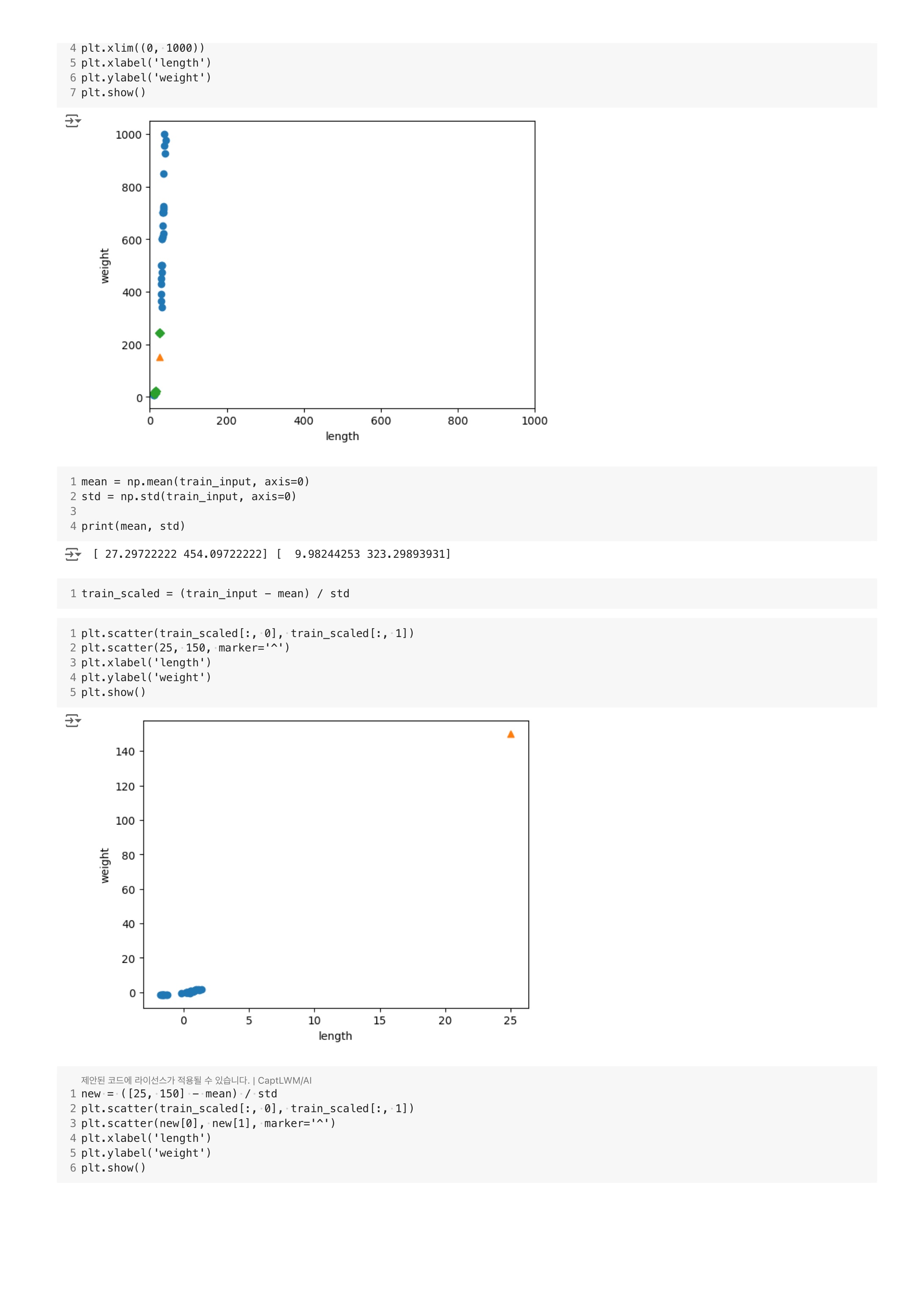
이렇게 되면 x 축은 영향을 미치지 못할 것이다.

이렇게 범위가 매우 다른 것을 스케일이 다르다고도 말한다. 따라서 특성 값을 일정한 기준을 맞춰줘야 한다.

이것을 데이터 전처리라고 부른다.

가장 널리 사용되는 전처리 방법은 표준점수이다. z 점수라고도 부르는 표준 점수는 각 특성값이 평균에서 표준편차의 몇 배 만큼 떨어져 있는지를 나타낸다.

계산은 평균을 빼고 표준편차를 나누어주면 된다.

mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)

print(mean, std)

평균과 표준 편차이다.

여기서 평균을 빼고 표준편차로 나누어 표준점수로 변환해보자.

train_scaled = (train_input - mean) / std

넘파이가 알아서 train_input의 모든 행에서 mean에 있는 두 평균 값을 빼준다. 그리고 std에 있는 두 표준편차를 다시 모든 행에 적용해준다.

이러한 기능을 브로드캐스팅 이라고 부른다.

plt.scatter(train_scaled[:, 0], train_scaled[:, 1])
plt.scatter(25, 150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()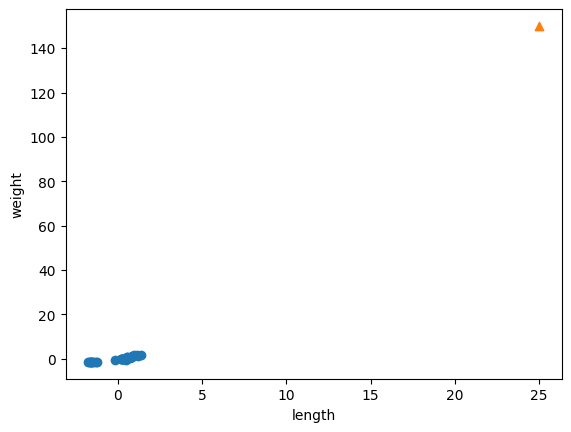

샘플도 동일한 비율로 변환해줘야 한다…

여기서 중요한 점은 훈련 센트의 mean, std를 이용해서 변환해야 한다는 점이다.

new = ([25, 150] - mean) / std
plt.scatter(train_scaled[:, 0], train_scaled[:, 1])
plt.scatter(new[0], new[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

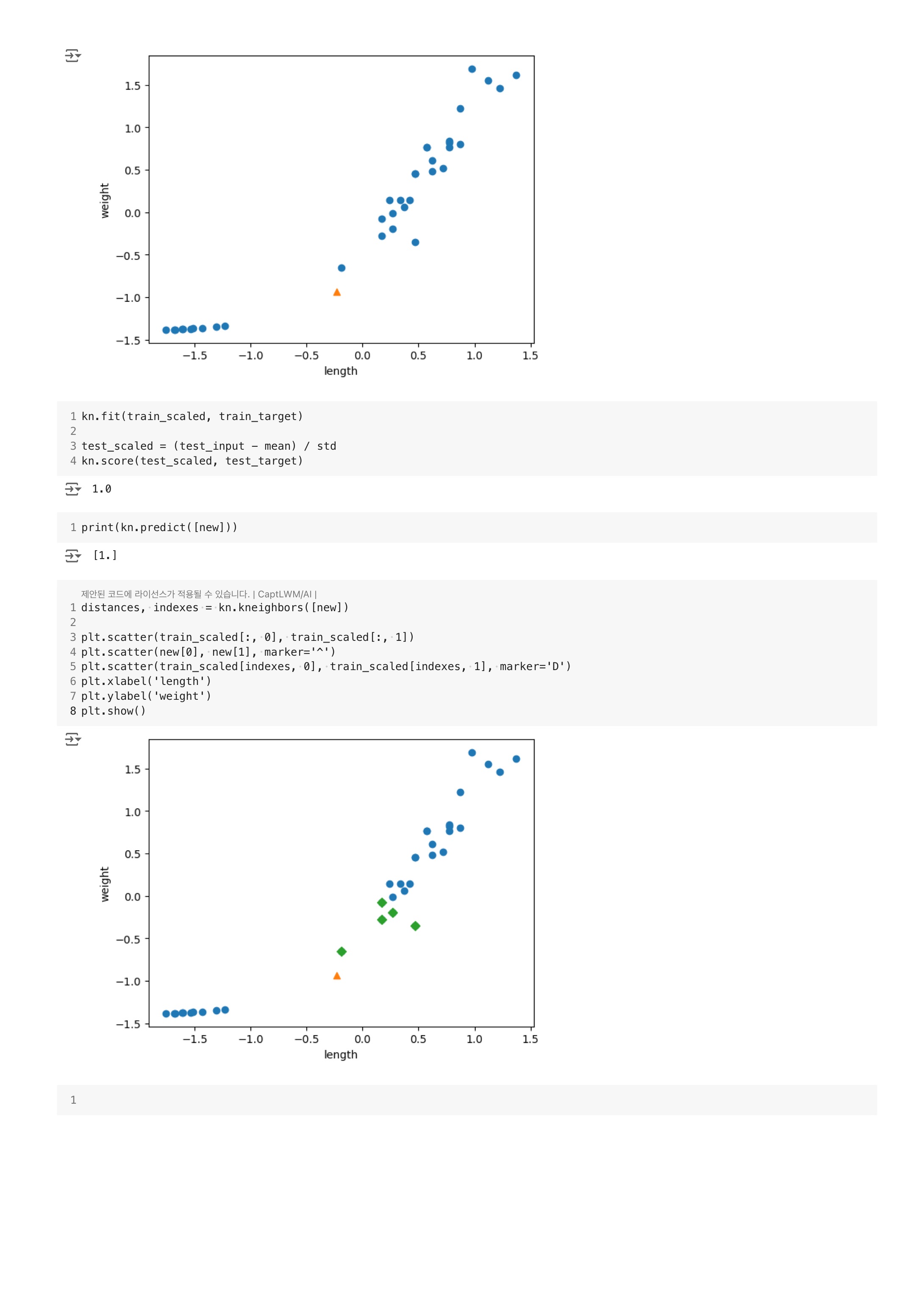
앞의 그래프와 거의 동일하지만 x, y축의 범위가 -1.5 ~ 1.5 사이로 바뀌었다는 것이다.

이제 다시 훈련해보자.

kn.fit(train_scaled, train_target)

test_scaled = (test_input - mean) / std
kn.score(test_scaled, test_target)

print(kn.predict([new]))

드디어 도미로 예측을 했다. 산점도로도 확인해보자.

distances, indexes = kn.kneighbors([new])

plt.scatter(train_scaled[:, 0], train_scaled[:, 1])
plt.scatter(new[0], new[1], marker='^')
plt.scatter(train_scaled[indexes, 0], train_scaled[indexes, 1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()

02-2. 확인 문제

미션