💡 미션 : Ch.04(04-1) 2번 문제 풀고, 풀이 과정 설명하기 + Ch.04(04-2) 과대적합/과소적합 손코딩 코랩 화면 캡처하기

04-1. 로지스틱 회귀

• 활용 : 럭키백에 포함된 물품의 확률을 구한다.
• K-최근접 이웃 : 주변 이웃의 클래스 비율을 확률이라고 출력하면 되지 않을까?
  • 사이킷런의 k-최근접 이웃 분류기 존재

확률

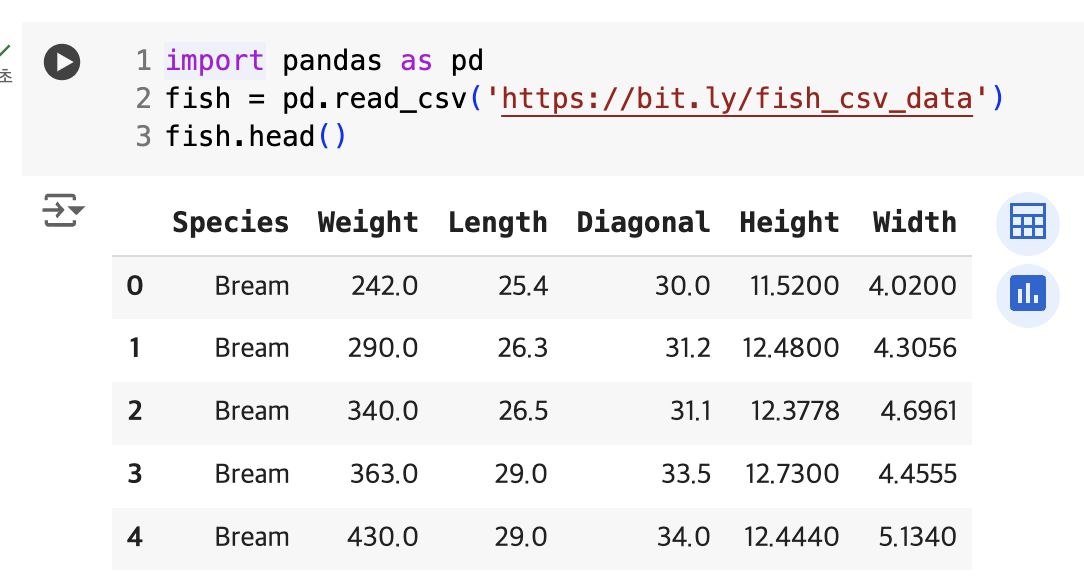
• read_csv() → csv파일을 데이터프레임을 ㅗ변환
• head() → 처음 5개 행 출력

• unique() → Species 열에서 고유한 값 추출

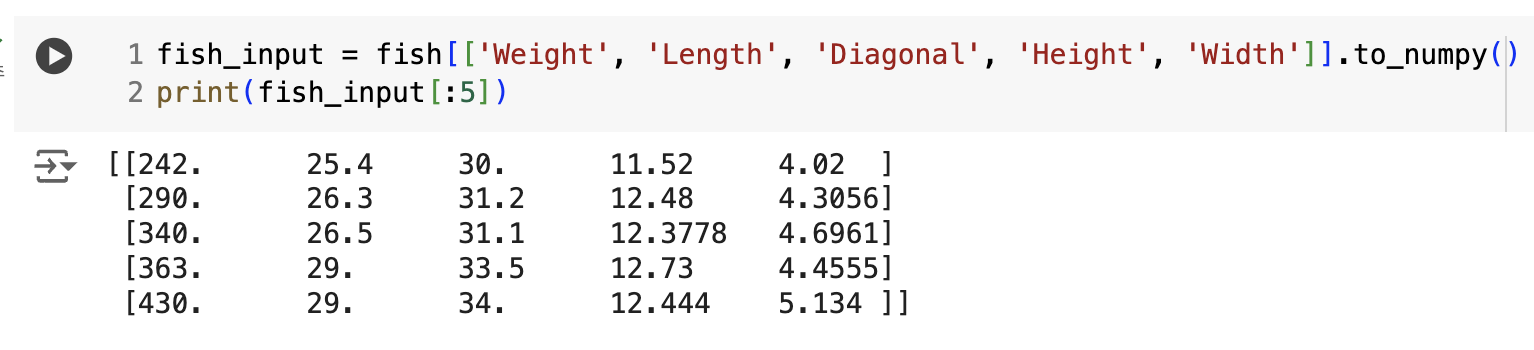
• Species 열을 제외한 나머지 열을 입력 데이터로 선택
• to_numpy() → 넘파이 배열로 바꿈

• train_test_split → 데이터 세트를 나눔
• StandardScaler → 훈련 세트의 통계 값으로 표준화 전처리.

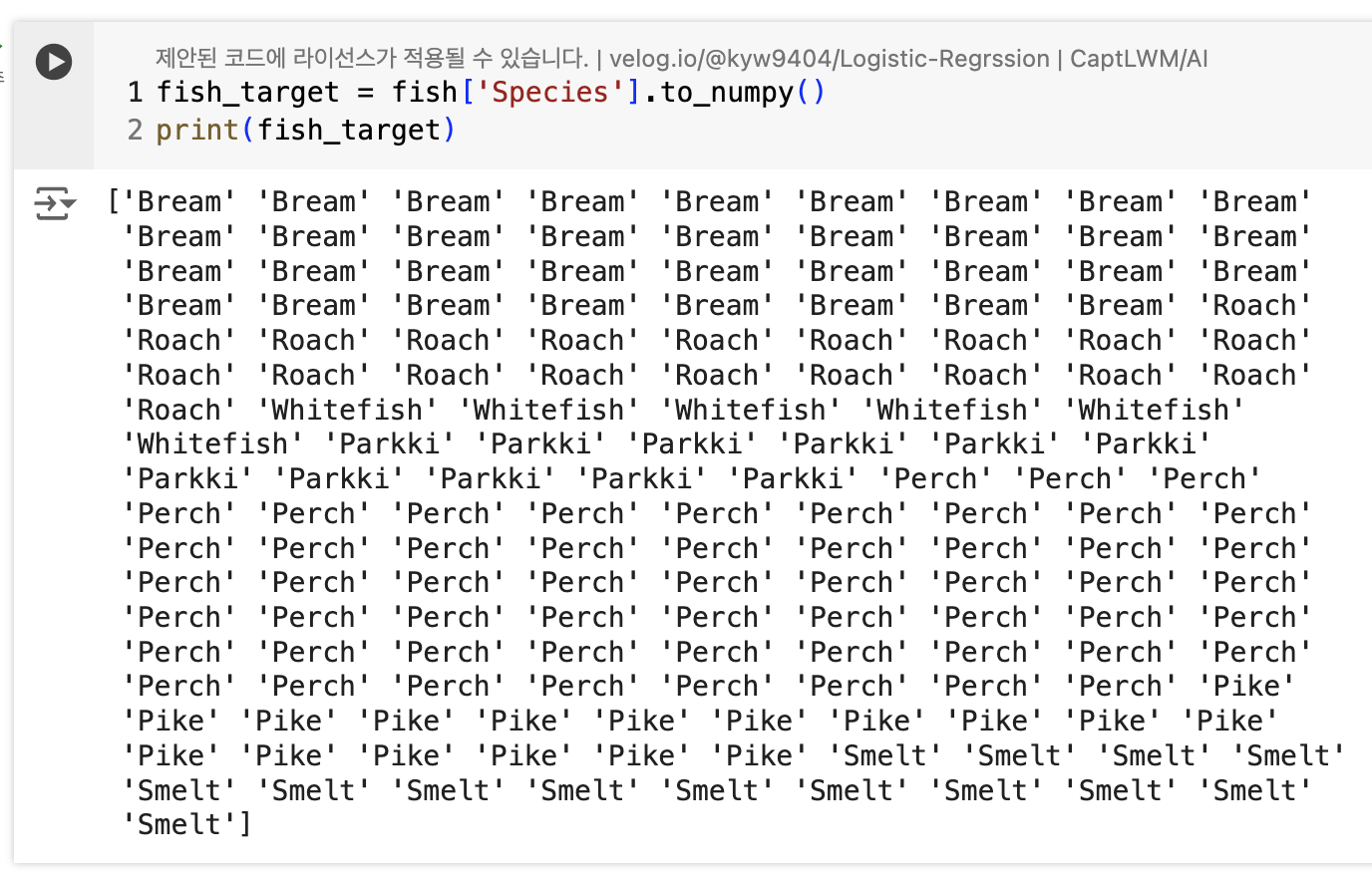
• 다중 분류(multi-class classfication) : 타깃 데이터에 2개 이상의 클래스가 포함된 문제
  • 훈련 방식은 이진 분류와 동일
  • 타깃 데이터를 1, 0이 아닌 문자열로 사용

• classes_ → 알파벳 순으로 정렬된 타깃값 저장
  

• predict() → 타깃값으로 예측 출력

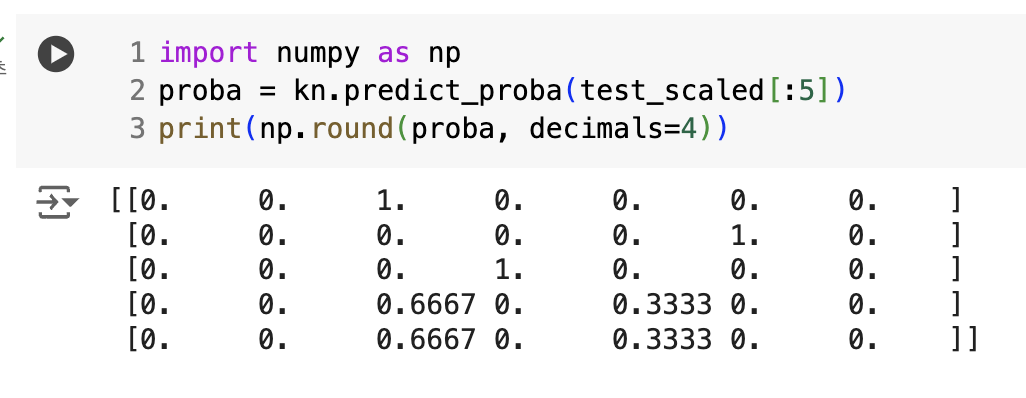
• predict_proba() → 클래스 별 확률값 반환
• round() → default=소수점 첫째 자리에서 반올림
  • decimals 매개변수로 소수점 아래 자릿수 지정
• 출력 순서는 classes_ 속성과 같다.

• Roach의 확률은 1/3인 0.33333
• Perch의 확률은 2/3인 0.66666

로지스틱 회귀

• \로지스틱 회귀(Logistic regression) : 이름은 회귀이지만 분류 모델, 선형 회귀와 동일하게 선형 방정식을 학습

• a, b, c, d, e → 가중치 혹은 계수
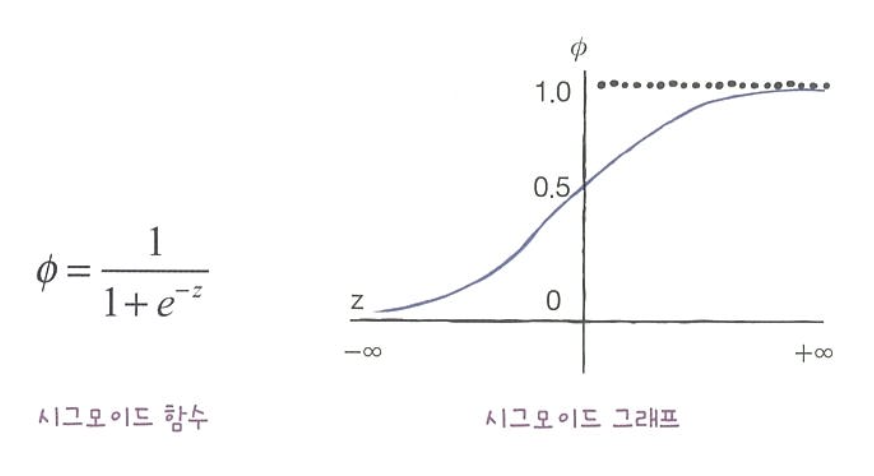
• 확률이 되려면 0~1 값 필요 → 시그모이드 함수(Sigmoid function) 또는 로지스틱 함수(Logistic Function)를 사용

• 불리언 인덱싱(Boolean Indexing) : True, False 값을 전달하여 행을 선택하는 것.

로지스틱 회귀로 이진 분류

• 불리언 인덱싱 적용

• 음성 클래스(0) = bream
• 양성 클래스(1) = smelt

• 로지스틱 회귀가 학습한 계수

• decision_function() → z값 출력 가능
• 이 z 값을 시그모이드 함수에 통과시키면 확률 획득
  

• expit() → 확률로 변환

로지스틱 회귀로 다중 분류

• max_iter 매개변수 → 반복 횟수 지정, default = 100
• 규제 → 릿지 회귀처럼 계수의 제곱을 규제 = L2규제
  • 규제 제어하는 매개변수 C
    • alpha와 반대로 작을수록 규제가 커진다.
    • default = 1

• 다중 분류는 소프트맥스 함수를 사용하여 7개의 z 값을 확률로 변환

시그모이드 함수는 하나의 선형 방정식의 출력값을 0~1 사이로 압축
소프트맥스 함수는 여러 선형 방정식의 출력값을 0~1 사이로 압축 + 전체 합 1이 되도록 만든다.
→ 정규화된 지수 함수

• deciion_function() → z값 계산

• axis : 소프트맥스 계산할 축 지정
  • axis=1 → 각 행에 대해 계산
  • 지정하지 않으면 배열 전체에 대해 계산

---

04-2. 확률적 경사 하강법

점진적인 학습

• 문제 : 훈련 데이터가 한 번에 준비되는 것이 아닌 조금씩 전달된다는 것
• 방법
  • 매일 추가되는 새로운 데이터로 모델 훈련 → 데이터가 늘어난다.
  • 새로운 데이터 추가할 때 이전 데이터를 버려 훈련 데이터 크기 일정하게 유지
  • 버리지 않고 새로운 데이터 조금씩만 더 훈련하기 = 점진적 학습(온라인 학습)
    • 대표적인 알고리즘 : 확률적 경사 하강법(Stochastic Gradient Descent)

확률적 경사 하강법

• 확률적 = 무작위하게 = 랜덤하게
• 경사 = 기울기
• 하강법 = 내려가는 방법

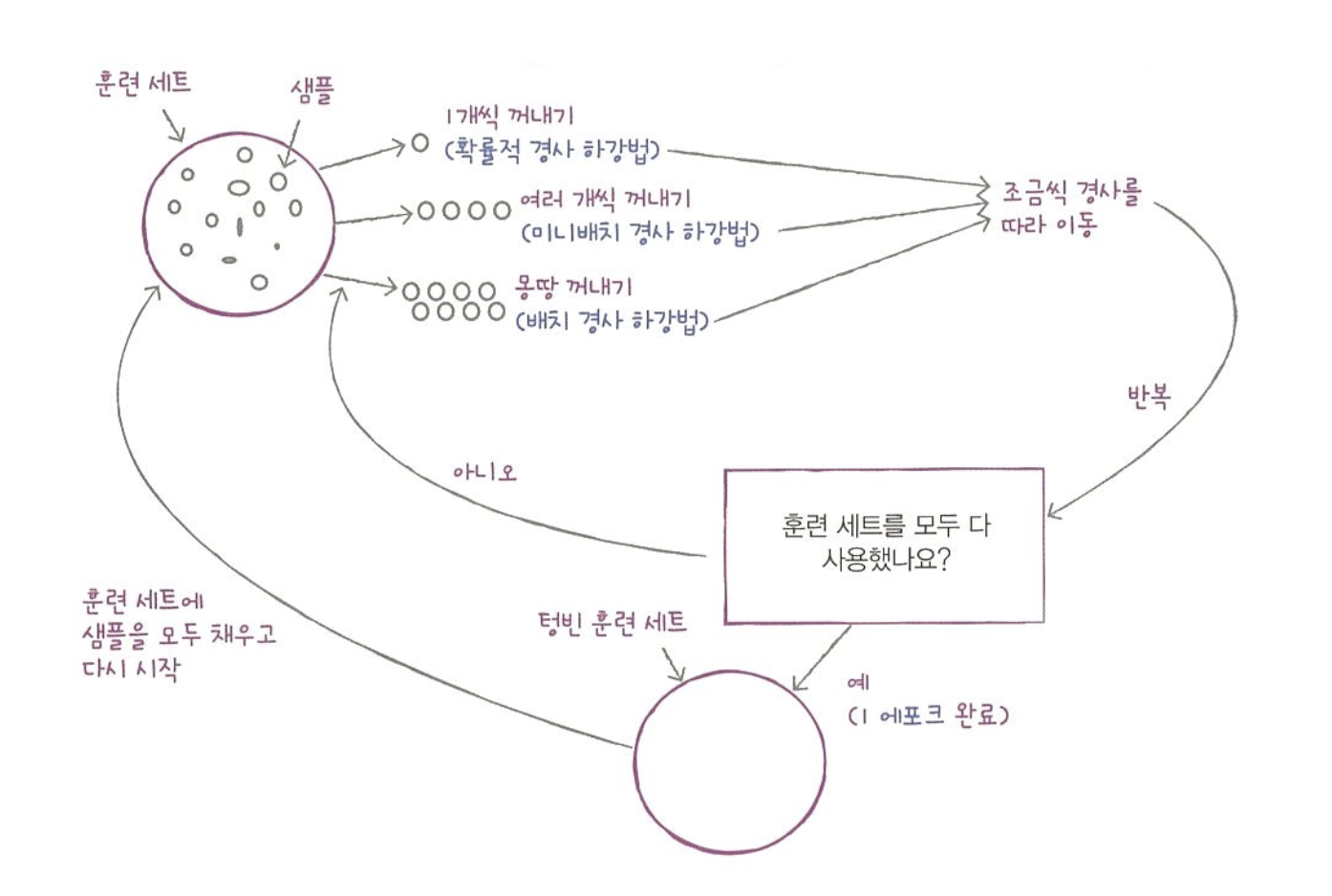
→ 훈련 세트에서 랜덤하게 하나의 샘플을 고르는 것

• 에포크(epoch) : 훈련 세트를 한 번 모두 사용하는 과정
• 미니배치 경사 하강법(minibatch gradient descent) : 하나의 샘플이 아닌 여러개의 샘플을 사용해 경사 하강법을 수행하는 방식
• 배치 경사 하강법(Batch gradient descent) : 극단적으로 한 번 경사로를 따라 이동하기 위해 전체 샘플을 사용하는 방식

손실 함수 Loss Function

손실함수는 머신러닝 알고리즘이 얼마나 엉터리인지를 측정하는 기준. 값이 작을 수록 좋다.

로지스틱 손실 함수(=이진 크로스엔트로피 손실 함수)

예측	정답(타깃)	예측 확률
1	1	0.9
0	1	0.3
0	0	0.2
1	0	0.8

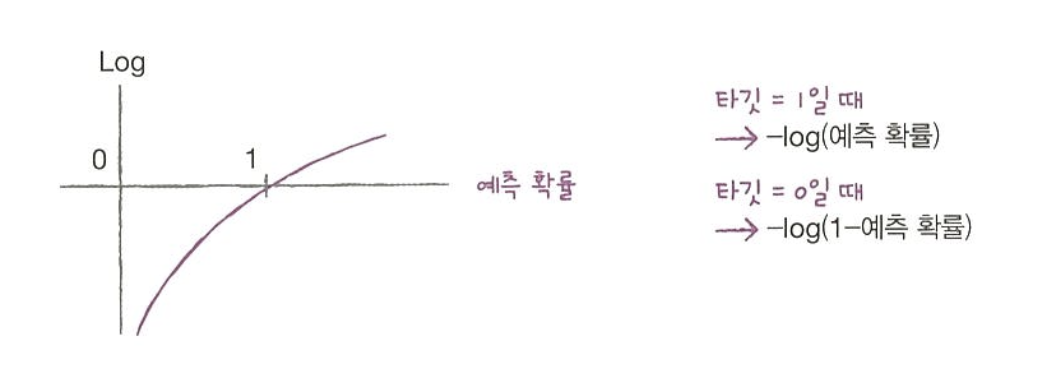
위 공식을 이용해서 손실 함수를 구해보자.

• 첫번째 샘플 : 0.9 X 1 → -0.9
• 두번째 샘플 : 0.3 X 1 → -0.3
• 세번째 샘플 : (1-0.2) X 1 → -0.8
• 네번째 샘플 : (1-0.8) X 1 → -0.2

여기에 로그함수를 적용하면 손실을 아주 크게 만들어 모델에 큰 영향을 미칠 수 있다.

• 다중 분류에 사용하는 손실 함수 ⇒ 크로스엔트로피 손실 함수(cross-entropy loss function)

SGDClassifier

• SGDClassifier : 확률적 경사 하강법 제공
  • loss 매개변수 : 손실 함수의 종류 지정
  • max_iter : 에포크 횟수

• partial_fit() : 모델 이어서 훈련할 때 사용

epoch, 과대/과소 적합

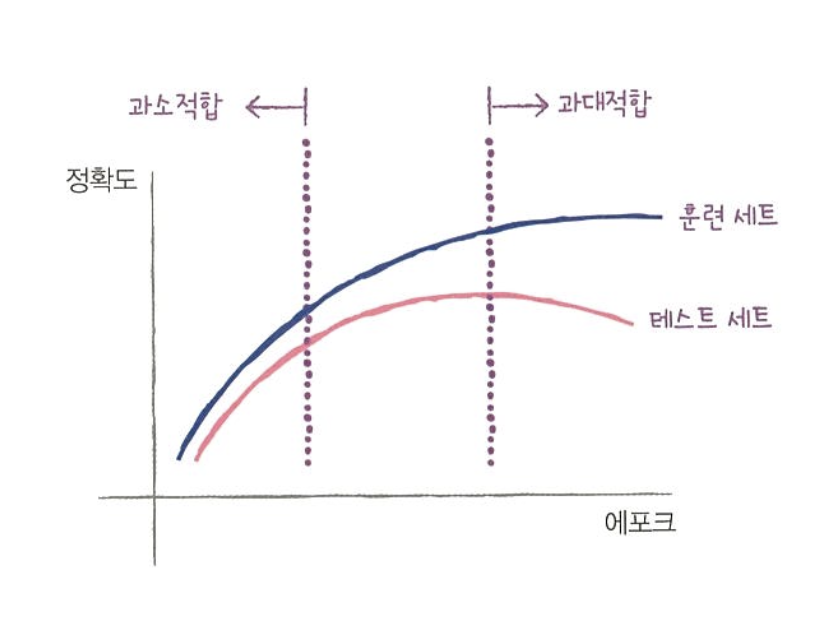
• 조기 종료(early stopping) : 과대적합이 시작되기 전에 훈련을 멈추는 것

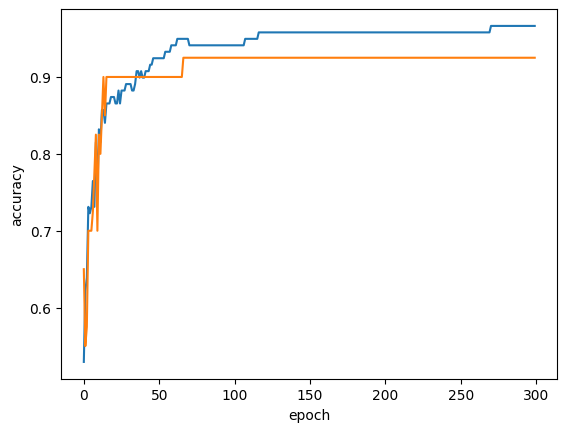
• 100번 째 에포크가 적절한 반복 횟수

• tol 매개변수 : 자동으로 멈추지 않고 무조건 max_iter만큼 반복
  • SGDClassifier는 일정 에포크 동안 성능이 향상되지 않으면 더 훈련하지 않고 멈추기 때문
• loss 매개변수
  - 기본값 = hinge
  - 힌지 손실(=서포트 벡터 머신)