🎯 leetcode - 207. Course Schedule
📌 문제
- 파이썬 알고리즘 인터뷰 39번 문제
📌 날짜
2020.02.10📌 시도 횟수
Failed💡 Code
class Solution(object):
def canFinish(self, numCourses, prerequisites):
graph = defaultdict(list)
for start, last in prerequisites:
graph[start].append(last)
print(graph)
traced = set()
def dfs(i):
# 만약 traced에 이미 저장된 경로를 재방문하면 프로그램 종료!
if i in traced:
return False
# 방문한 경로를 traced에 저장하기
traced.add(i)
# 갈 수 있는 경로가 1개 이상인 경우
for y in graph[i]:
# dfs 재귀를 지나면서 traced에 경로가 쌓임
if not dfs(y): # traced의 경로를 재방문해서 return 됨
return False
traced.remove(i) # 모든 가능한 경로를 다 탐색하면 remove하기
return True
# 여기는 외부 함수에서 dfs를 부르는 곳
# graph의 key를 기준으로 ⭐모든 key에 대한⭐ 경로를 탐색한다!
for x in list(graph): # 모든 각각의 (start, last)에 대해 dfs 탐색
if not dfs(x): # 한번이라도 탐색이 중반에 종료되면
return False # 바로 return False함
return True💡 문제 해결 방법
- 역으로 trace하는 것을 유의해서 이해하자.
[1, 0]이면 1 ← 0이고, 1부터 traced에 저장해서 역방향으로 1을 가리키는 0을 그 다음에 traced에 저장한다. - 대략적인 설명은 주석에 적어놓았다.
- 대신 코드를 이해하기 위해 그림으로 그려보면서 이해했다.
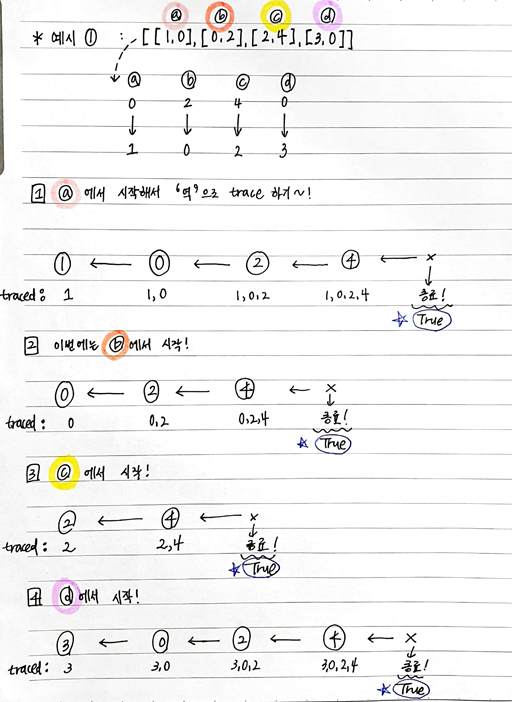
[[1, 0], [0, 2], [2, 4], [3, 0]]인 경우 →True가 나온다.
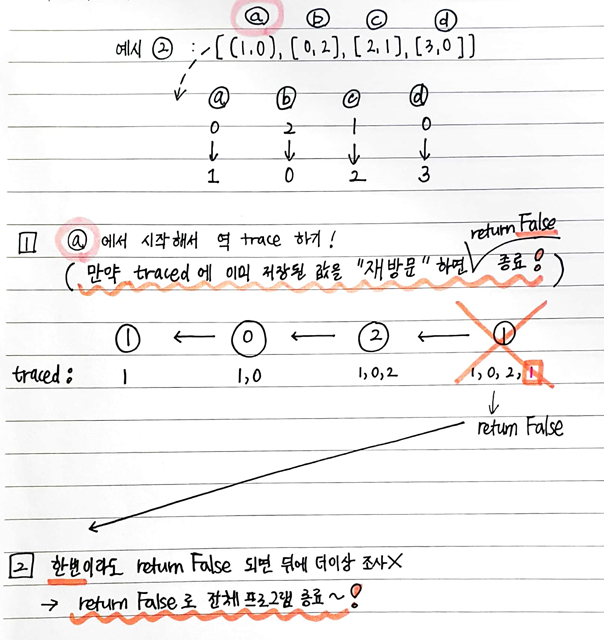
[[1, 0], [0, 2], [2, 1], [3, 0]]인 경우 →False가 나온다.
🌵 추가 설명
🤯 만약
[[1, 0], [0, 2], [1, 3]]인 경우에는?
- dfs안의 for문이 살짝 헷갈려서 과정을 하나하나 적어보았다.
하나의 key에 대해 여러 value가 있는 경우 (하나의 목적지로 가는 코스가 2개 이상인 경우)가 헷갈려서 해보았다.graph = defaultdict(<class 'list'>, {1: [0, 3], 0: [2]})이다.x: 1 # 먼저{1: [0, 3], 0: [2]}의 1부터 시작한다. .......traced : {1} # 1을 방문했으니까 traced.add(1) -> y: 0 # 1의 첫번째 value인 0부터 방문한다. .......traced : {0, 1} # 0을 방문했으니까 traced.add(0) -> y: 2 # 0의 첫번째 value인 2를 방문 .......traced : {0, 1, 2} # 2를 방문했으니까 traced.add(2) # 2의 value는 존재하지 않는다. # ※return to 0 / traced.remove(2)※ # 0의 value는 존재하지 않는다. # ※return to 1 / traced.remove(0)※ -> y: 3 # 1의 두번째 value인 3을 방문 .......traced : {1, 3} # 3를 방문했으니까 traced.add(3) # 3의 value는 존재하지 않는다. # ※return to 1 / traced.remove(3)※ # 1의 value는 존재하지 않는다. # ※return True※ x: 0 # 위에와 같은 방법으로 진행 .......traced : {0} -> y: 2 .......traced : {2, 0} True # 모든 dfs가 True를 반환했으므로 return True
😆 최적화하기
- 모든 경로가 직렬 + 하나로 이어져 있는 코스일 경우, 위의 방법으로는 이전 key에서 이미 방문한 경로임에도 시작점(key)이 다르기 때문에 다시 탐색해야 되는 비효율성이 존재한다.
예를 들어 {0: [1], 1: [2], 2: [3], 3: [4]}는 0←1←2←3←4 임에도 매번 0←1←2←3←4 / 1←2←3←4 / 2←3←4 ...를 모두 탐색해야 된다. - 따라서 visited를 추가하여 한번 방문했던 코스는 다시 방문하지 않도록 무조건 True로 리턴하는 구조를 위의 코드에 추가했다.
💡 Code
class Solution(object):
def canFinish(self, numCourses, prerequisites):
graph = defaultdict(list)
for start, last in prerequisites:
graph[start].append(last)
traced = set()
visited = set()
def dfs(i): # 1
if i in traced:
return False
if i in visited:
return True
traced.add(i)
for y in graph[i]:
if not dfs(y):
return False
traced.remove(i)
visited.add(i)
return True
for x in list(graph):
if not dfs(x):
return False
return True