40. Network Delay Time

🎯 leetcode - 743. Network Delay Time

---

📌 문제

- 파이썬 알고리즘 인터뷰 40번 문제
- 최단 경로 탐색: 다익스트라 알고리즘 활용

📌 날짜

2020.02.13

📌 시도 횟수

5 try / Failed

💡 정답 Code

from collections import defaultdict
import heapq


class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        # graph 생성
        graph = defaultdict(list)
        for n1, n2, sec in times:
            graph[n1].append((n2, sec))
            
        Q = [(0, k)]
        dist = defaultdict(int)
        
        while Q:
            time, node = heapq.heappop(Q)
            if node not in dist:
                dist[node] = time
                for n2, sec in graph[node]:
                    alt = time + sec
                    heapq.heappush(Q, (alt, n2))
                    
        if len(dist) == n:
            return max(dist.values())
        return -1

💡 문제 해결 방법

- 아래의 과정을 천천히 이해해보자.
- 파이썬의 heapq는 min heap의 결과를 저장한다는 점!
- 따라서 "최소 힙부터 pop"되므로 time이 높은 값은 결국 나중에 
"dist에 이미 값이 존재한다고 판단"되므로 버려지게 된다는 점을 유의하자.

0. graph를 생성하면 다음과 같다.
   
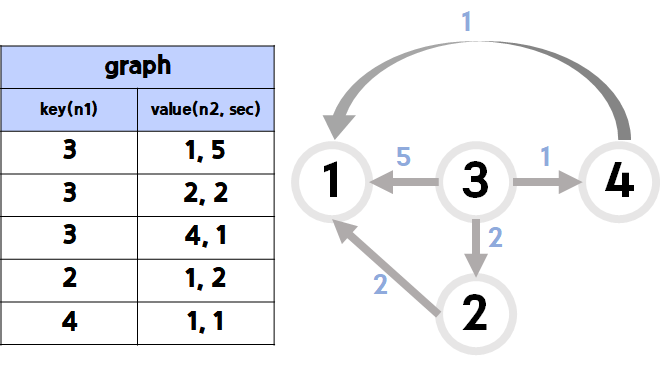
1. Q와 dist를 생성하고 초기화한다.
   heapq.heappop(Q)한 결과를 dist에 저장한다.
   
2. 방금 heappop한 Q의 node와 인접한 노드들을 Q에 넣는다.
   이때 새롭게 Q에 넣는 인접한 노드들의 time 값은,
   "이전의 연결된 노드(3)의 time 값(0)" + "graph에 저장된 sec값"이 되도록 한다.
   즉, 이전에 연결된 노드들의 time값도 더해져서 누적된 값을 Q에 넣는 time 값이 되도록 한다.
   
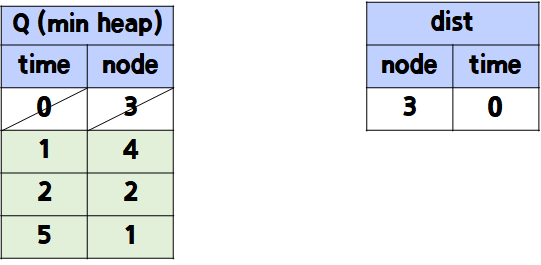
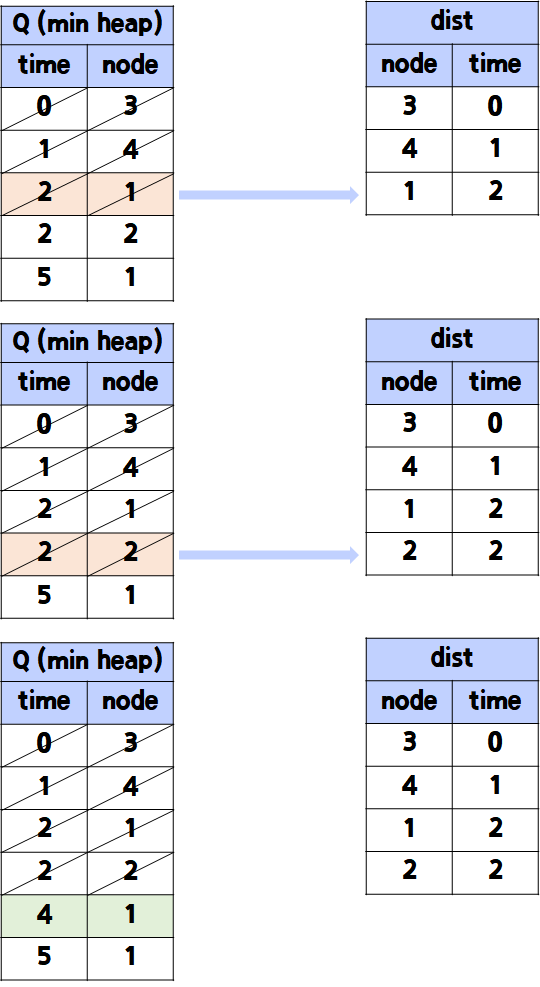
3. 다시 heappop해서 dist에 넣는다.
   
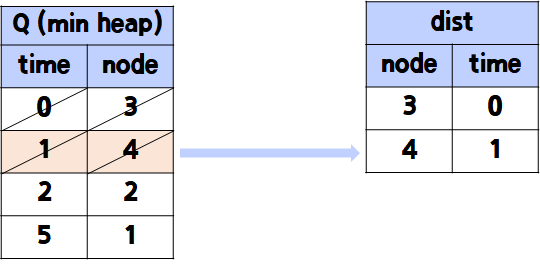
4. 다시 heappop한 노드와 인접한 노드들을 Q에 추가한다.
   마찬가지로 Q에 추가할 때에는 해당 인접한 노드의 time 값이 이전 노드의 time값을 합친 누적값이 되도록 한다.

• graph[4]의 sec는 1이지만, dist[4]의 time이 1이므로, 따라서 최종적으로 (node = 1, time = 1+1 = 2)를 Q에 추가함.
  

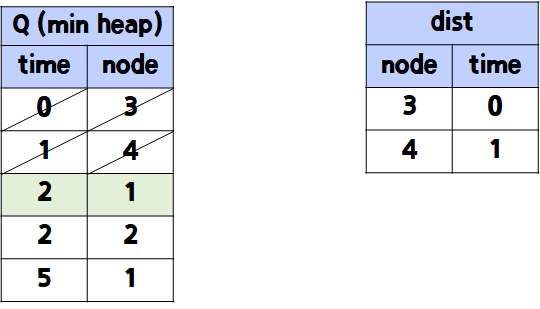
5. 계속 위의 과정을 반복
   
6. 만약 Q에서 heappop한 것의 node가 이미 dist에 존재한다면 과감히 버리고 넘어간다.
   
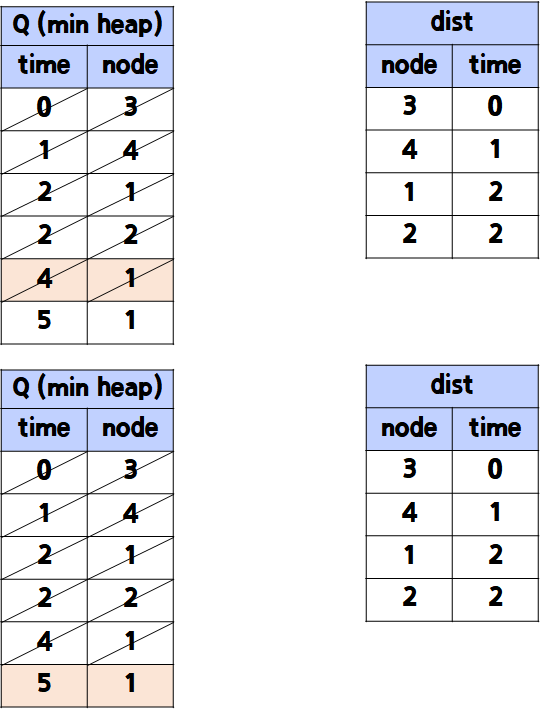
7. 따라서 최종 결과는 dist = {3: 0, 4: 1, 1: 2, 2: 2}이고 len(dist) == n이므로 dist의 value(time) 값들의 max 값인 2를 리턴한다.

---

💡 새롭게 알게 된 점

- 다익스트라 알고리즘의 형태와 활용에 대해 조금 이해하게 되었다.
- 이런 풀이의 형태에 좀 더 익숙해져야겠다.

❌ (한번에 맞추지 못한 경우) 오답의 원인

- ㅎㅎ 최단 경로 문제 처음 풀어봤다. 
bfs를 이리저리 바꿔봤지만 계속 오류가 나서 결국 책을 봤다😹