✍️ 그래프
그래프(Grpah)란? 그래프 G는 (V, E)로 표시
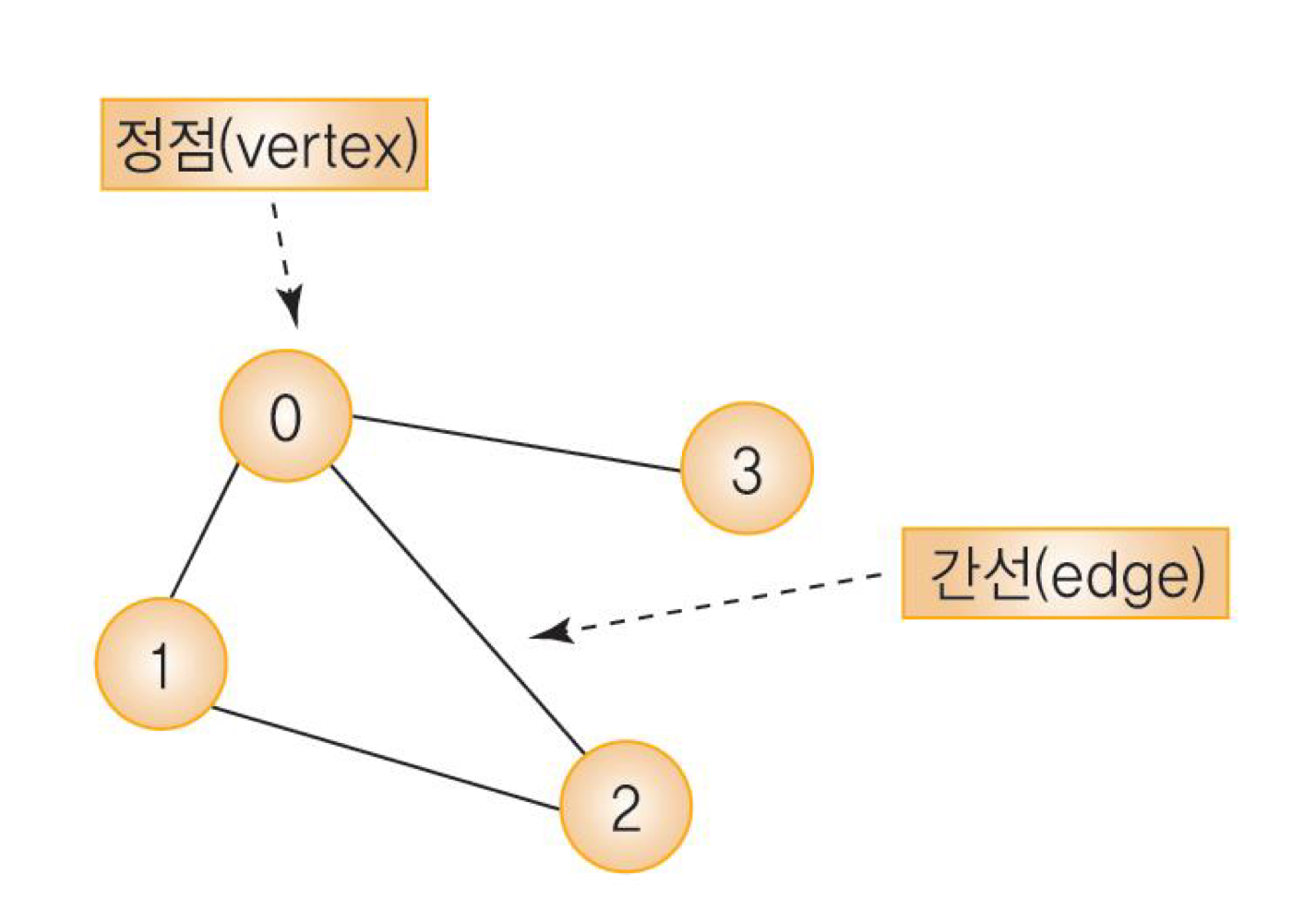
정점(vertex): 여러 가지 특성을 가질 수 있는 객체 의미. 노드(node)라고도 불린다.
간선(edge): 정점들 간의 관계 의미. 링트(link)라고도 불린다.
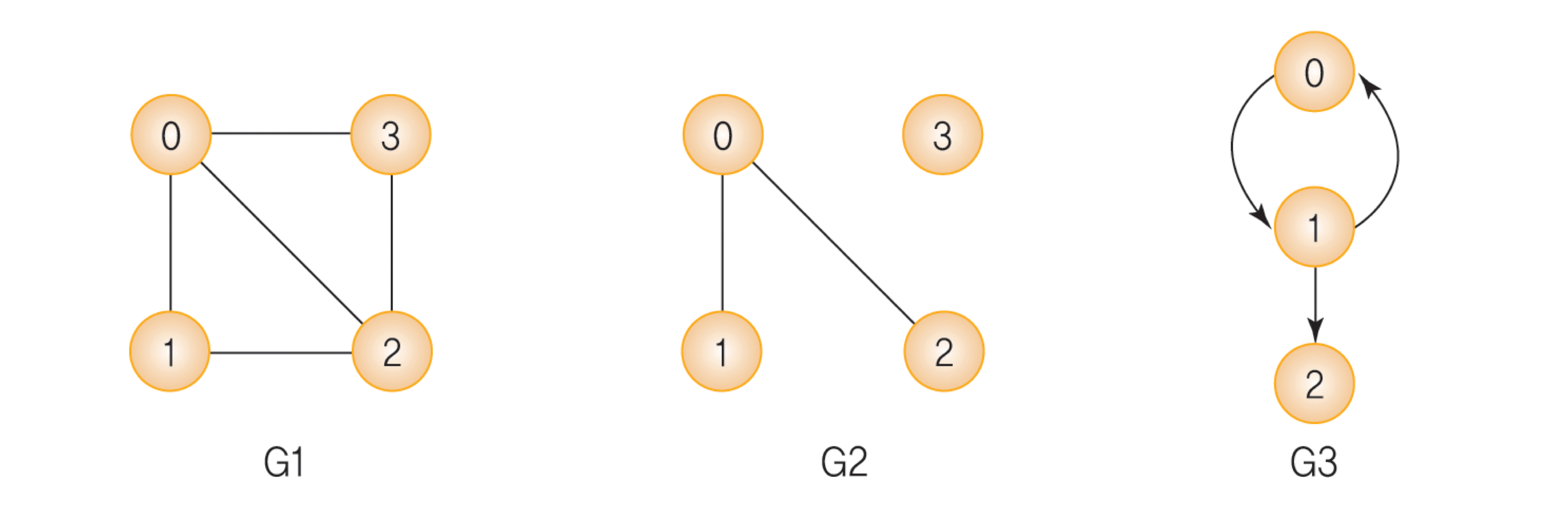무방향 그래프와 방향 그래프의 차이가 존재한다.
V(G1) = {0, 1, 2, 3}, E(G1) = {(0, 1), (0, 2), (0, 3), (1, 2), (2,3)}
V(G2) = {0, 1, 2, 3}, E(G2) = P(0, 1), (0, 2)}
V(G3) = {0, 1, 2}, E(G3) = {<0, 1>, <1, 0>, <1, 2>}
부분 그래프(subgraph)
정점 집합 V(G)와 간선 집합 E(G)의 부분 집합으로 이루어진 그래프
인접 정점(adjacent vertex)
간선에 의해 직접 연결된 정점
tree에서의 차수는 자식이 몇명 있는지를 의미하고, graph에서의 차수는 인접한 정점이 몇개 있는지를 의미한다.
그래프의 경로(path)
무방향 그래프의 정점 s로부터 정점 e까지의 경로
단순 경로(simple path): 경로 중에서 반복되는 간선이 없는 경로
사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경로
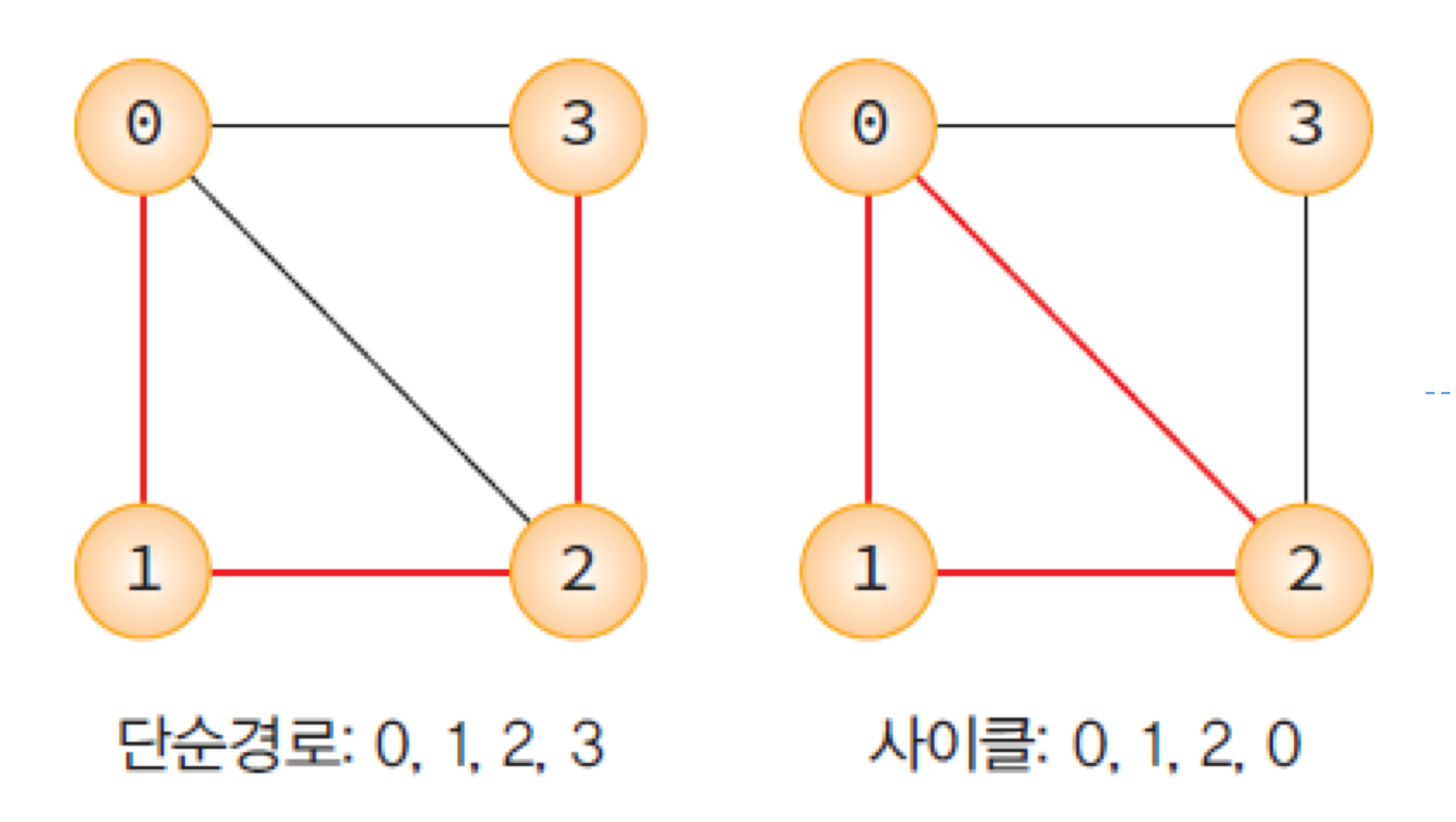
G1의 0, 1, 2, 3은 경로지만 0, 1, 3, 2는 경로가 아니다.
G1의 1, 0, 2, 3은 단순경로이지만 1, 0, 2, 0은 단순경로가 아니다.
G1의 0, 1, 2, 0과 G3의 0, 1, 0은 사이클이다.
연결 그래프(connected graph)
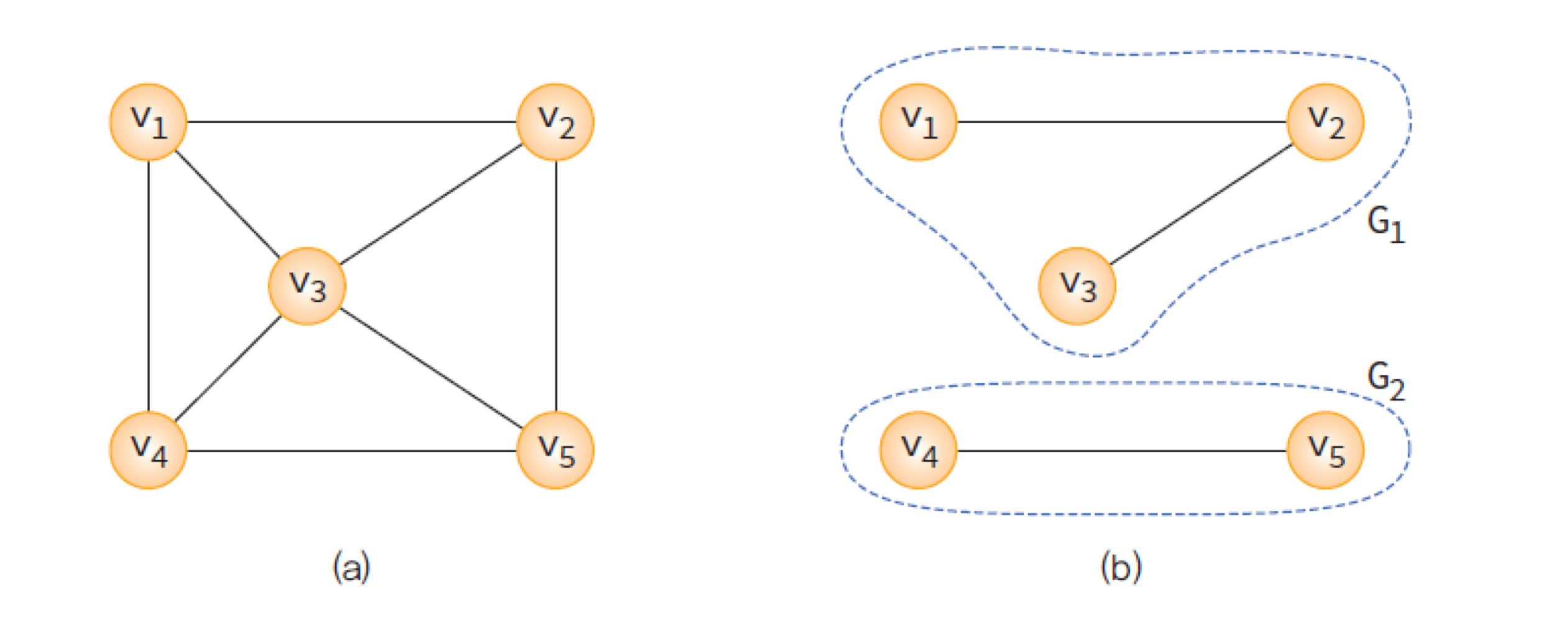
(a)는 무방향 그래프 G에 있는 모든 정점쌍에 대하여 항상 경로가 존재한다.
(b)는 비연결 그래프이다.
트리는 그래프의 특수한 형태로서 사이클을 가지지 않는 연결 그래프이다.
완전 그래프(complete graph)
모든 정점이 연결되어 있는 그래프
무방향 완전 그래프의 간선의 수는? (총 정점 * (총 정점 - 1) ) / 2
why? 무방향 그래프이기 때문에 / 2를 한다. 왔다갔다를 하나로 친다.
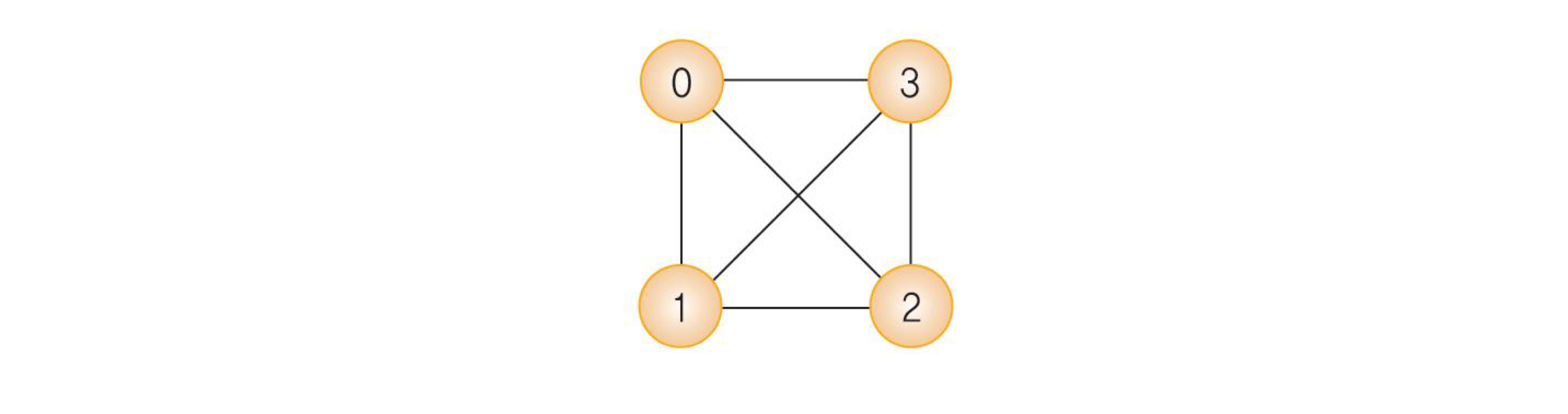
✍️ 그래프의 표현방법
간선이 많으면? 배열로 구현하는 게 좋다.
간선이 몇개 없으면? 리스트로 구현하는 게 좋다.
🔍 인접행렬(adjacent matrix) 방법
if(간선 (i, j)가 그래프에 존재) M[i][j] = 1,
그렇지 않으면 M[i][j] = 0을 한다.
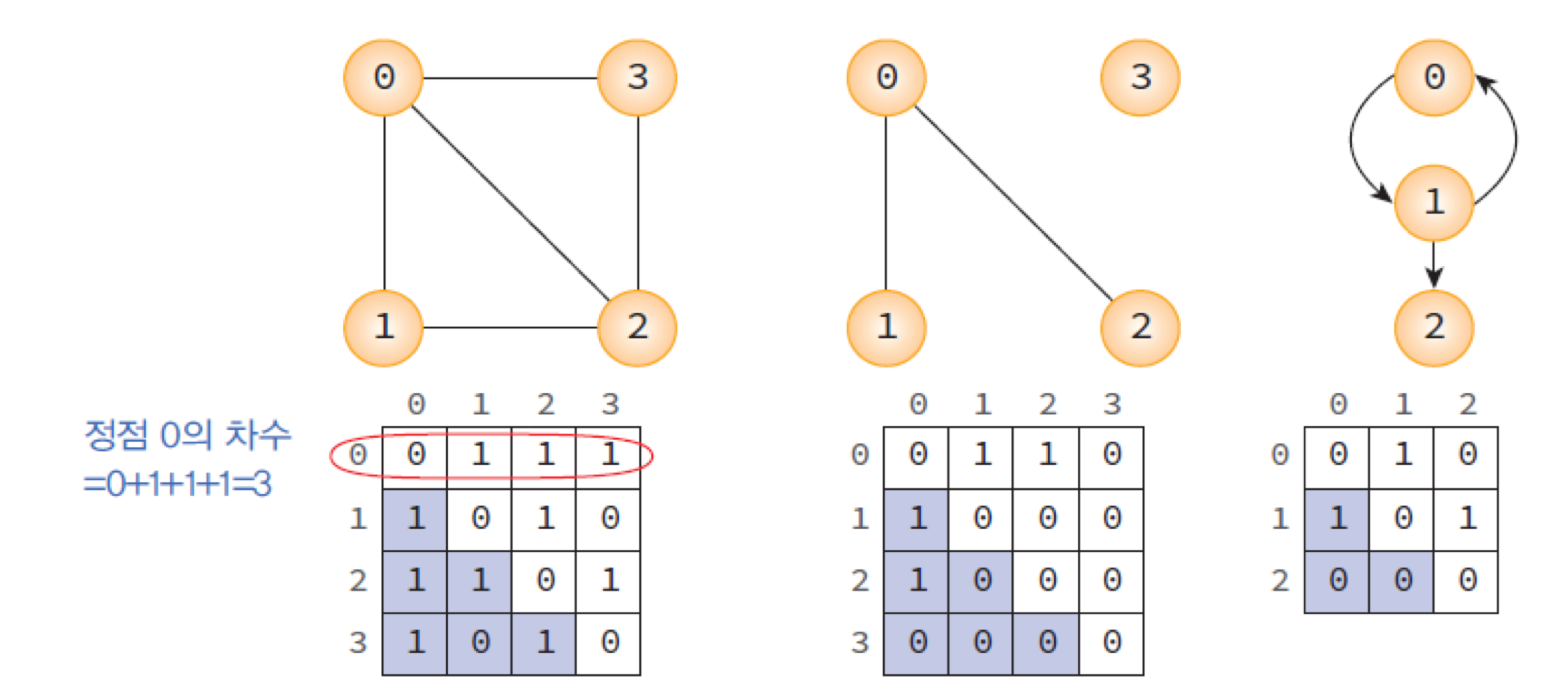무방향 그래프는 대칭적으로 만들어진다.
🔍 인접 리스트(adjacent list) 방법
각 정점에 인접한 정점들을 연결리스트로 표현한다.
간선의 개수가 적은 희소그래프(sparse graph)의 표현에 적합하다.
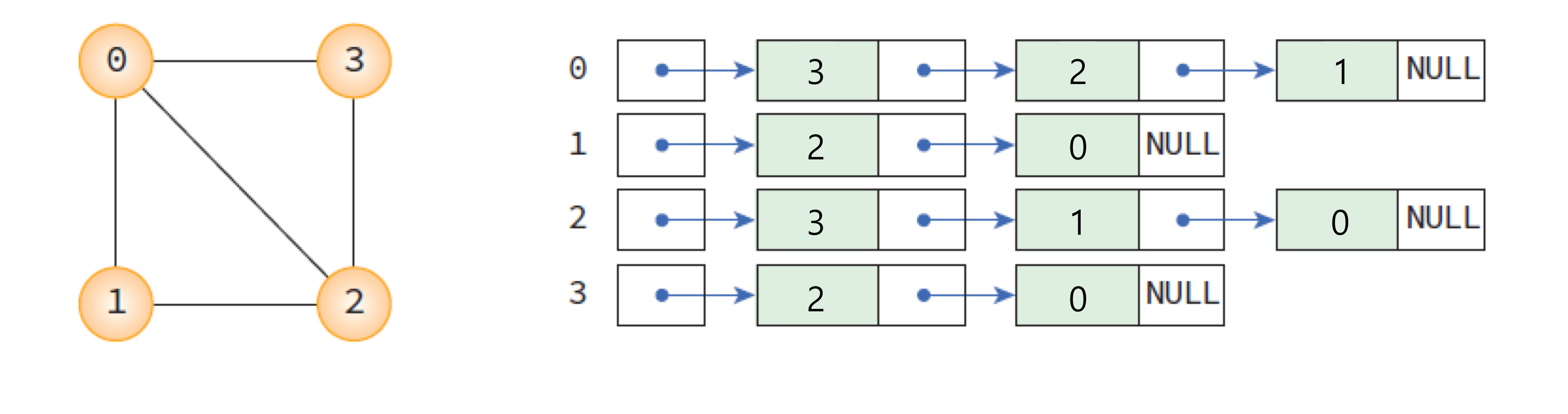무방향 그래프는 간선 하나당 두번 쓰인다.
차수를 구하고 싶으면? 간선의 수만큼 필요하다.
✍️ 그래프 탐색
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한번씩 방문하는데 queue 또는 stack을 사용하여 구현할 수 있다.
🔍 깊이 우선 탐색(DFS: depth first search)
stack을 사용한다.
한 방향으로 갈 수 있을 때까지 가다가 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행한다.
되돌아가기 위해서 순환함수 호출로 묵시적인 스택을 이용한다.
인접 행렬과 인접 리스트 각각 구현할 수 있는데 실행하면 순서가 다름을 알 수 있다.
시간복잡도는
인접 행렬: O(n^2)
인접 리스트: O(n+e)
이다.
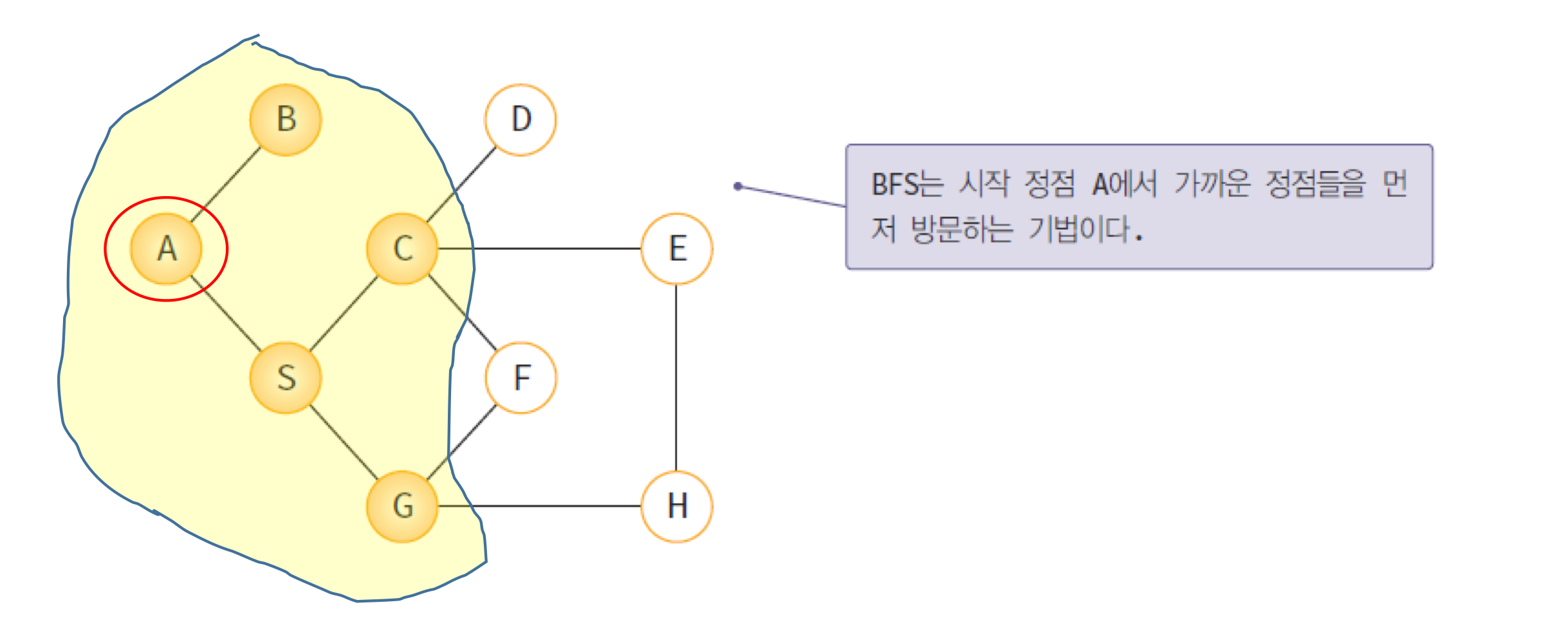
🔍 너비 우선 탐색(BFS: breadth-first search)
queue를 사용한다.
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다.
인접 행렬과 인접 리스트 각각 구현할 수 있는데 실행하면 순서가 다름을 알 수 있다.
시간복잡도는
인접 행렬: O(n^2)
인접 리스트: O(n+e)
이다.
