✍️ 최소비용 신장 트리(minimum spanning tree)
신장 트리(spanning tree)란? 그래프 내의 모든 정점을 포함하는 트리
n개의 정점을 가지는 그래프의 신장 트리는 n-1개의 간선을 가진다.
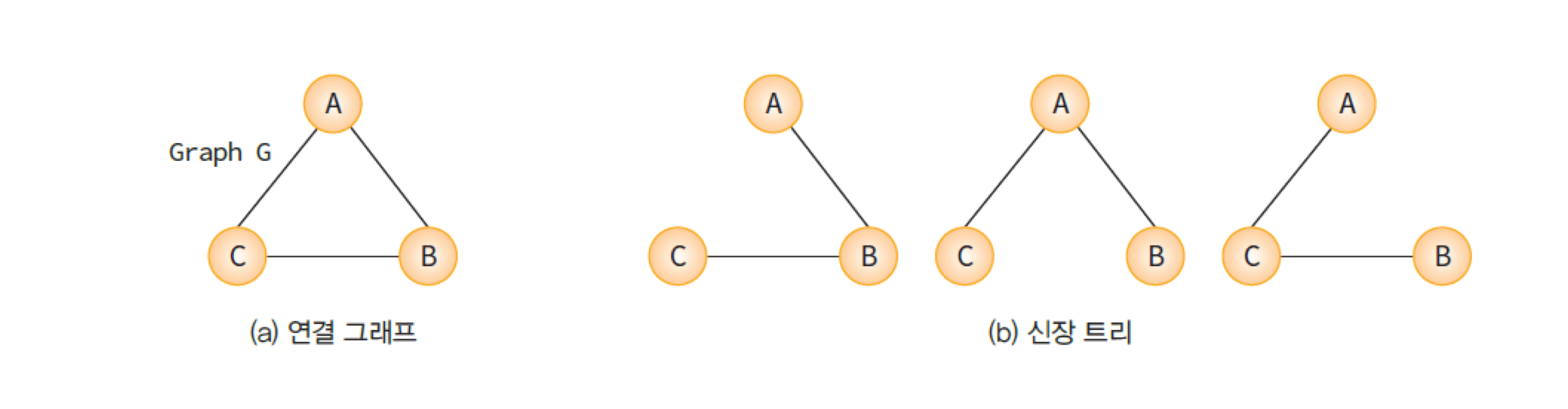
그렇다면 최소비용 신장 트리는 최소의 비용으로 모든 정점을 연결 즉, 가장 적은 수의 간선과 비용으로 모든 정점들을 연결한 것이다. 비용이 같은 게 존재한다면 최소비용 신장 트리는 여러개일 수도 있다.
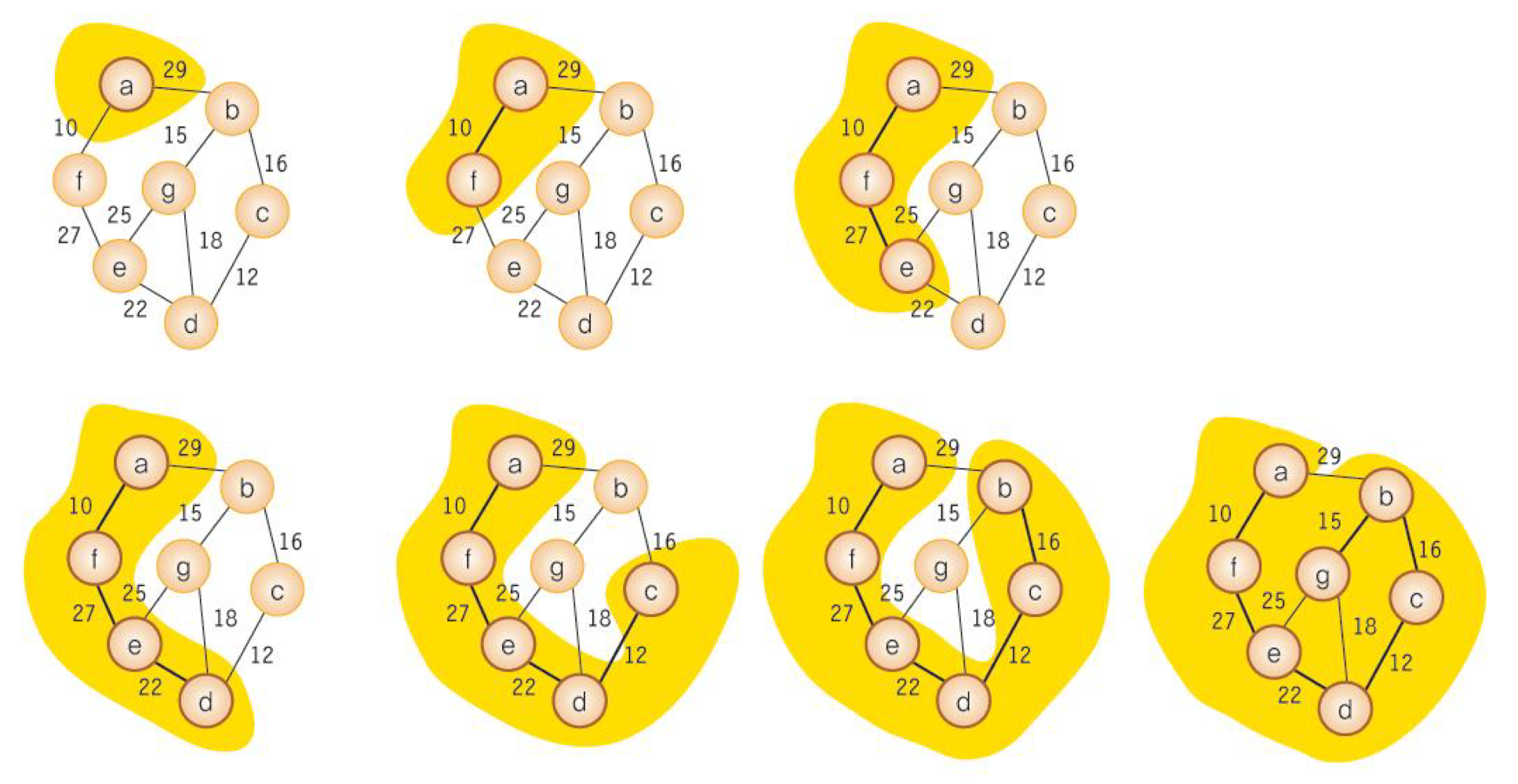
✍️ Kruskal의 MST 알고리즘
🔍 탐욕적인 방법(greedy method)
각 단계에서 최선의 답을 선택하는 과정을 반복함으로써 최종적인 해답에 도달할 수 있다.
항상 최적의 해답을 주는지 검증이 필요하다. Kruskal MST 알고리즘은 최적의 해답임이 증명된다.
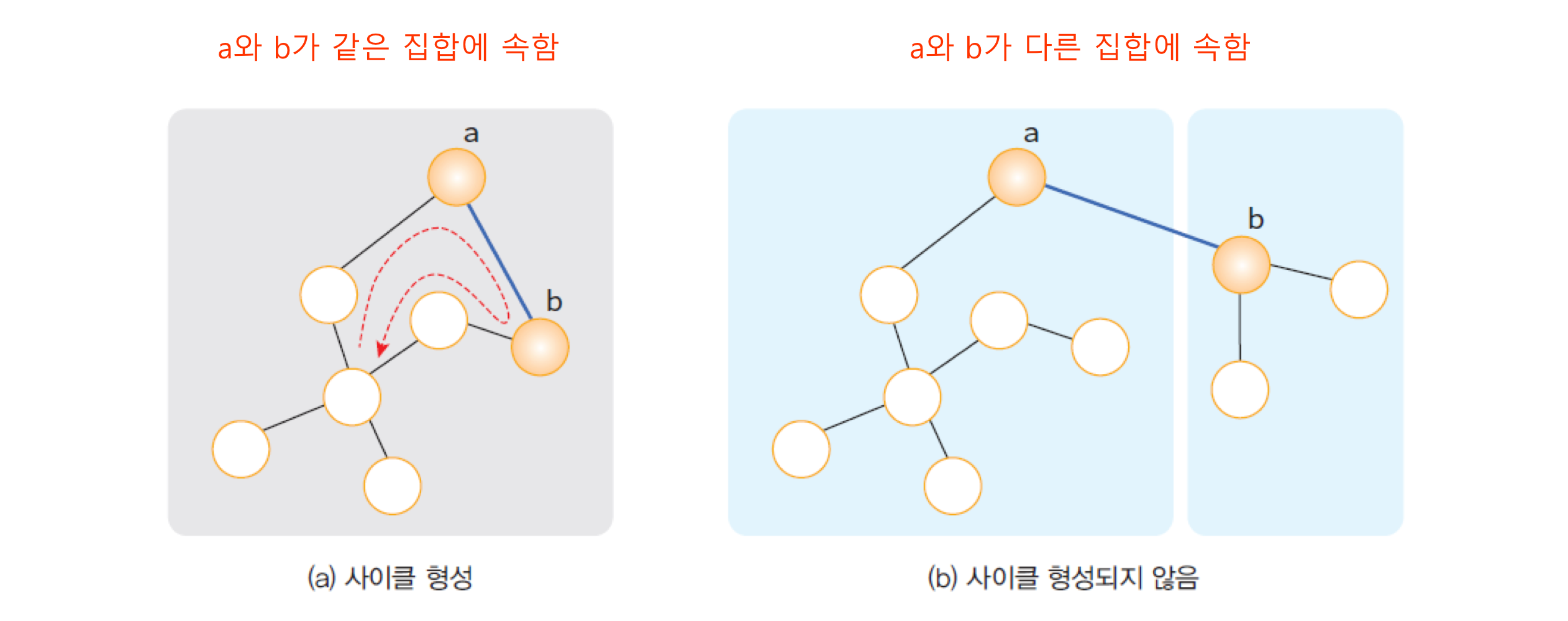
🔍 union-find 알고리즘
원소가 어떤 집합에 속하는지 알아낸다. Kruskal의 MST 알고리즘에서 사이클 검사에 사용된다.
🔍 Kruskal의 MST 알고리즘 복잡도
Kruskal 알고리즘은 대부분 간선들을 정렬하는 시간에 좌우된다. 사이클 테스트 등의 작업은 정렬에 비해 매우 신속하게 수행된다.
네트워크의 간선 e개를 퀵정렬과 같은 효율적인(?) 알고리즘으로 정렬한다면 Kruskal 알고리즘의 시간 복잡도는 O(e*log(e))가 된다.
✍️ Prim의 MST 알고리즘
시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해나간다.
신장 트리 집합에 인접한 정점 중에서 최저 간선으로 연결된 정점을 선택하여 신장 트리 집합에 추가한다.
🔍 Prim의 MST 알고리즘 복잡도
주 반복문의 정점의 수 n만큼 반복하고, 내부 반복문의 n번 반복하므로 Prim의 알고리즘은 O(n^2)의 복잡도를 가진다.
✍️ 최단 경로
최단 경로란(shortest path)? 네트워크에서 정점 u와 정점 v를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로
최단 경로 알고리즘
- Dijkstra 알고리즘: 하나의 시작 정점에서 다른 정점까지의 최단 경로를 계산
- Floyd 알고리즘: 모든 정점에서 다른 모든 정점까지의 최단 경로를 계산
🔍 Dijkstra의 최단 경로 알고리즘
하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는다.
- 매 단계에서 가장 distance 값이 작은 정점을 S에 추가
- 각 단계에서 S 안에 있지 않은 정점 중에서 가장 distance 값이 작은 정점을 S에 추가
- 새로운 정점이 S에 추가되면 distance 값 갱신
집합 S? 시작 정점 v로부터의 최단 경로가 이미 발견된 정점들의 집합
distance 배열? 최단 경로가 알려진 정점들만을 이용한 다른 정점들까지의 최단 경로 길이
🔍 Dijkstra의 최단 경로 알고리즘 복잡도
네트워크에 n개의 정점이 있다면, Dijkstra의 최단 경로 알고리즘은 주 반복문을 n번 반복하고 내부 반복문을 2n번 반복하므로 O(n^2)의 복잡도를 가진다.
