1. 이변량 분석 - 숫자와 숫자
1.1 이변량 분석이란?
- 두 개의 변수 간의 관계를 분석하는 통계적 방법
- 두 변수가 어떻게 서로 연관되어 있는지, 상관관계나 의존성을 확인하는데 사용
- 목적
- 하나의 변수가 다른 변수에 미치는 영향을 평가하는 것
- 이를 통해 변수 간의 상관 관계나 원인 - 결과 관계를 탐구할 수 있음
1.2 숫자 vs 숫자 정리하는 방법
- 그대로 점을 찍어서 그래프를 그려봄 (산점도)
- 각 점들이 얼마나 직선에 모여 있는지를 계산
- 공분산
- 상관계수
1.2.1 산점도
-
두 숫자형 변수의 관계를 나타내는 그래프
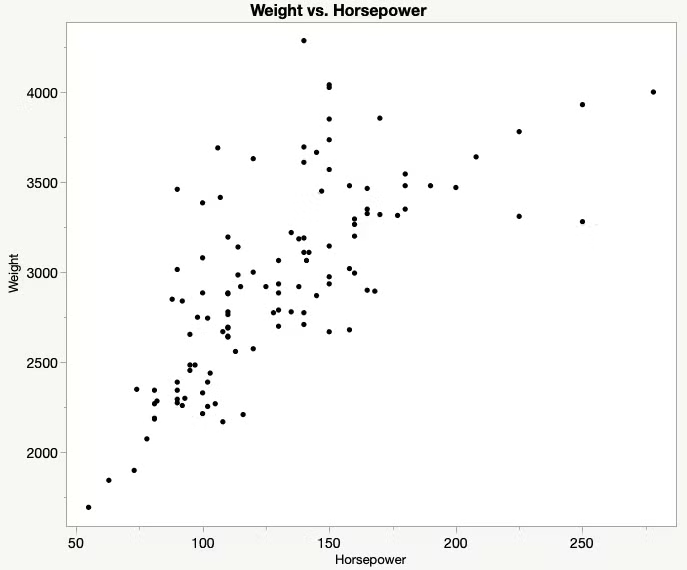
먼저 직선의 관계를 살펴봐라!
숫자 vs 숫자를 비교할때 중요한 관점 - 직선 -
matplotlib
- plt.scatter(x축 값, y축 값)
- plt.scatter('x 변수','y 변수',data=data)
-
seaborn
- sns.scatter('x 변수','y 변수',data=data)
강한 관계와 약한 관계
-
얼마나 직선에 모여있는가
-
x와 y의 관계를 얼마나 직선으로 잘 설명할 수 있는가
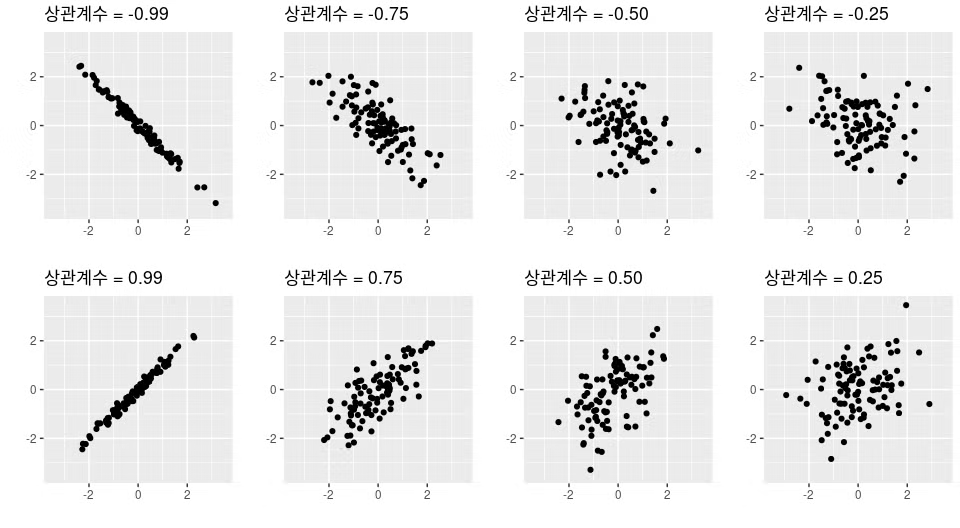
-
산점도 한번에 그리기
- sns.pairplot(dataframe)
- 숫자형 변수들에 대한 산점도를 한번에 그려줌
- 단점 : 변수와 데이터가 많다면 시간이 많이 걸리고 일일이 확인하기 쉽지 않음
1.3 상관계수, 상관분석
- 눈으로 그래프를 살펴보며 관계를 파악하는 것이 쉽지 않을 수 있다
- 관계를 확실히 따지고 싶다면 관계를 숫자로 계산해서 비교해보아라
- 관계를 수치화 -> 상관계수
- 상관계수가 유의미한지를 검정 (test)-> 상관분석
1.3.1 상관계수
-
상관계수는 r로 표현됨
-
-1~1 사이의 값
-
상관계수끼리 비교 가능
-
-1,1에 가까울 수록 강한 상관관계를 나타냄
-
경험에 의한 대략적인 기준 (절대적인 기준이 아님)
- 강한 0.5≤|r|<1
- 중간 0.2≤|r|≤0.5
- 약한 0.1≤|r|≤0.2
- 거의 없음 |r|<0.1
상관계수의 유의성 검정
- 상관계수의 크기로 판단할 수 있지만, 상관분석을 통해 검정(test)할 수 있음
import scipy.status as spst
spst.pearsonr(변수,변수)-
피어슨 상관분석
- NaN이 있으면 계산되지 않음(결측값 제거후 계산)
- 결과(상관계수,p-value)
-
상관계수 한번에 구하는 방법 - df.corr()
-
상관계수의 한계
- 상관계수는 직선의 관계(선형관계)만 수치화
- 고려하지 않는 두가지 : 직선의 기울기, 비선형 관계
- 상관계수는 직선의 관계(선형관계)만 수치화
1.4 p-value(유의확률)
-
어떻게 사용하는지에 초점
-
그래프로 관계를 파악하는데 한계가 있기 때문에 관계를 수치한 값(상관계수)가 유의미한지 판단하는 숫자
p-value<0.05이면, 두 변수간에 관계가 있다(상관계수가 의미가 있다)
p-value≥0.05이면, 두 변수간에 관계가 없다 (상관계수가 의미가 없다)
2. 평균추정과 신뢰구간
-
분산 (Var,Variance), 표준편차(SD,Standard Deviation)
- 한 집단을 설명하기 위해서, 대푯값으로 평균을 계산했을때
- 값들이 평균으로부터 얼마나 벗어나 있는지를 나타내는 값 (이탈도, deviation)
2.1 조사방법
- 표본조사
- 추출 방식: 많은 수, 무작위
- 장점 : 적절한 비용과 시간
- 단점 : 오차가 존재
- 전수조사
- 전체(모집단) 조사
- 장점 : 정확! 오차0
- 단점 : 비용, 시간 과다
2.2 표본을 뽑는 목적(Sampling)-> 모집단 추정
- 표본을 가지고 어떤 통계량을 계산한다면, 그 목적은 모집단을 추정하기 위함
- 표본평균
- 모평균에 대한 추정치
- 추정치에는 오차가 존재 = 표준오차
2.3 중심극한의 정리
- 평균들의 (x1,x2,x3,,,,)의 분포(표집 분포) → 정규분포에 가까워짐
- 표본의 데이터 수 (표본의 크기) ≥ 30개
- 이 분포의 평균(평균들의 분포): 모평균에 근사
표본의 크기가 ㅡㄹ수록 정규본포 모양이 중심에 가까워지는 좁은 형태가 됨
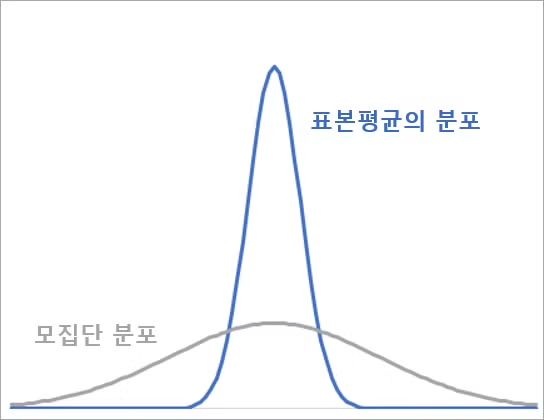
2.4 95% 신뢰구간
- 표준오차를 바탕으로 95% 확률 구간을 구할 수 있음
- x1으로 모평균을 추정할때
- 95% 신뢰구간
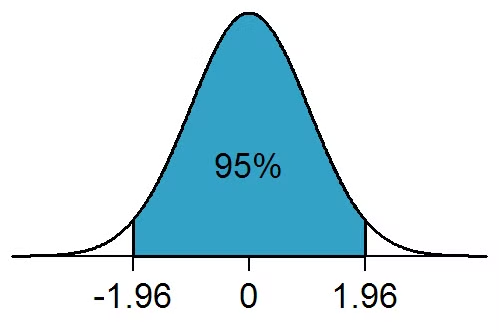
- 쉬운설명 : 신뢰 구간안에 모평균이 포함될 확률 895%
- 정확한 설명 : 표본을 100번 정도 뽑으면 95번 정도는 95% 신뢰 구간안에 모평균 포함
