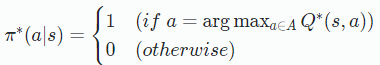오늘 살펴볼 내용은 강화학습에서 가장 중요한 내용인 MDP 와 Bellman Equation이다.

Agent는 현재 state에서 자신이 가진 Policy로 Action을 취해 그로부터 Reward를 얻고 state가 바뀐다. Environment는 Agent가 Action을 취할 때 Reward와 다음 state를 제공한다. Agent의 목표는 얻은 Reward의 누적 합을 최대화하는 것인데 이때 환경을 MDP(Markov Decision Process)로 정의하고 Bellman Equation을 통해 누적 보상을 계산한다. 보통 Reward의 누적 합을 최대화 하기 위해 얻은 Reward를 가지고 Policy를 수정한다.(상을 많이 받으면 고수 Exploitation 상이 적으면 새로운 길을 모색 Exploration) 이때 심층 신경망을 이용하는 방식을 심층 강화학습(Deep Reinforcement Learning)이라고 하며 최근 강화학습에서 가장 많이 이용되는 방법이다.

1 MDP

마르코프 결정 과정은 의사결정 과정을 모델링하는 수학적인 틀이다. 바로 MDP를 정의하면 복잡하기 때문에 MDP 보다 간단한 의사결정 과정을 살펴보며 점점 개념을 확장해 나가자.
우선 그전에 Markov라는 단어가 붙은 의사 결정은 다음 성질을 만족한다.

• Markov Property

  $P(s_{t+1}|s_t)=P(s_{t+1}|s_0,s_1,...,s_t)$
  이때 "어떤 상태 $s_t$ 는 'Markov'하다.
  쉽게 말해 다음 상태를 예측하는데 현재 상태만 필요 하다는 뜻이다.
  Markov Property를 따르면 미래를 예측하는데 고려해야 할 변수들이 줄어들기 때문에 모델의 복잡도가 줄어든다.

• MP (Markov Process)

  MP는 $(S,P)$ 로 이루어진 tuple이다.

  $S: finite\;state\;set$
  $P: state\;transition\;matrix$
  $P_{ss*}=P(s_{t+1}=s^*|s_t=s)$

하지만 여기에는 보상이 빠져있다. 보상이 없으면 Agent는 자신의 Policy를 평가하고 수정할 수 없다. MP에 보상 변수가 추가된 의사 결정 과정을 MRP 라고 한다. (Markov Reward Process)

• MRP(Markov Reward Process)

  MRP는 $(S,P,R,\gamma)$로 이루어진 tuple이다.

  $S:finite\;state\;set$
  $P:state\;transition\;matrix,P \in \mathbb{R}^{|S| \times |S|}$
  $P_{ss*}=P(s_{t+1}=s^*|s_t=s)$
  $R: reward, R:S \rightarrow \mathbb{R}$
  $\gamma \in [0,1]$ discount factor

  Agent의 목표는 자신이 놓인 환경에서 행위를 하며 얻은 누적 보상의 합을 최대화 하는 것이다. 즉,
  $G_t=r_t+\gamma r_{t+1} + \gamma^2 r_{t+2}+...$ 를 최대화 하는 것이다. 이때 $G_t$를 Return이라고 하며 $\gamma$는 할인률이다. $\gamma$값을 설정하는 이유는 agent가 무한한(이론적으르) 행위를 했을 때 Return이 발산하는 것을 막기 위함이다. 또한 $\gamma$에 따라 미래 보상의 중요도가 결정되기 때문에 강화학습에서 중요한 hyper-parameter다. 보통 0.9~0.99로 설정한다.

하지만 MRP에는 Agent의 Action이 정의되지 않았다. MRP에서 Action을 추가한 의사 결정 구조를 MDP라고 하며 Policy도 MDP에서 정의된다.

• MDP(Markov Decision Process)

  MDP는 $(S,A,P,R,\gamma)$로 이루어진 tuple이다.

  $S:finite\;state\;set$
  $A: finite\;action\;set$
  $P:state\;transition\;matrix,P\in \mathbb{R}^{|A| \times |S| \times |S|}$
  $P_{ss*}^a=P(s_{t+1}=s^*|s_t=s,a_t=a)$
  $R: reward, R:S\times A \rightarrow \mathbb{R}$
  $\gamma \in [0,1]$ discount factor
  $Policy: \pi(a| s)=P(a_t=a | s_t=s)$

MP에서 시작해 개념을 확장하며 MDP에 대하여 알아보았다. 정리하자면 MDP 안에서 Agent는 행위를 하며 얻은 보상의 누적값을 최대화 하기 위해 Policy를 수정한다. 하지만 MDP에서 $P,\pi$는 보통 stocahstic(확률)하기 때문에 $G_t=r_t+\gamma r_{t+1} + \gamma^2 r_{t+2}+...$를 그대로 사용할 수 없고 Return의 기댓값을 최대화하는 것으로 목표가 바뀐다. 이때 Return의 기댓값을 가치 함수라고 한다.

2 Value Function

MDP는 확률적이기 때문에 Return값을 그대로 사용할 수 없고 Return의 기댓값을 사용한다. 이것을 가치함수라고 하며 Agent는 가치함수를 최대화하기 위해 Policy를 수정한다. Value fucntion에는 V-function , Q-function 두 가지가 있는데 의사 결정 트리를 통해 직관적으로 이해할 수 있다.

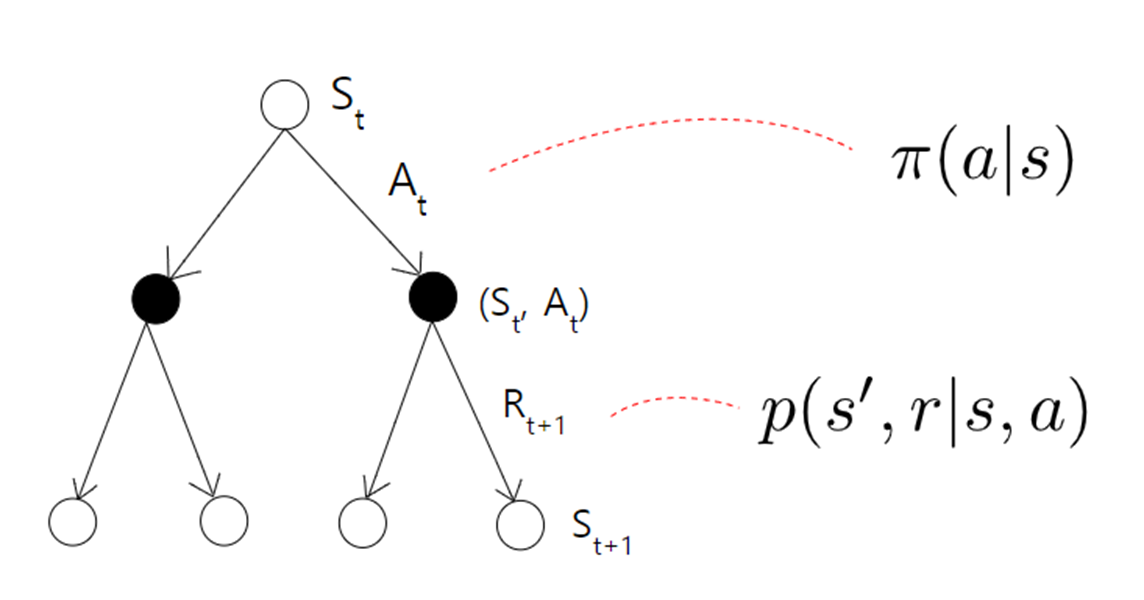
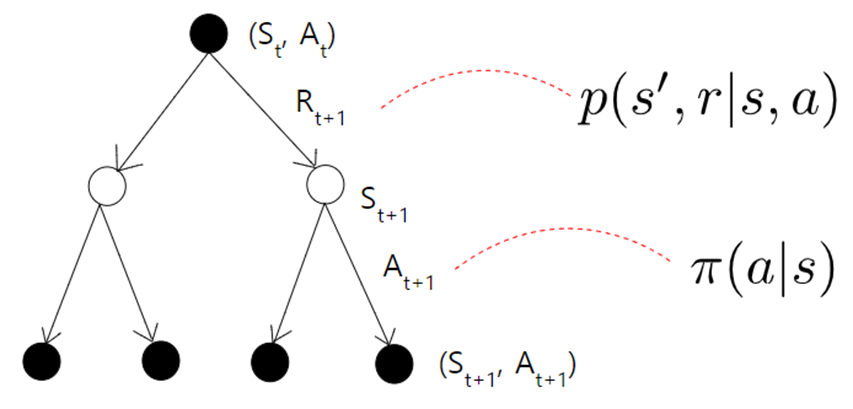
V는 현재 $s_t$ 상태에 놓였을 때(조건부 확률) 그 이후부터 Return의 기댓값이고
Q는 현재 $s_t$ 상태에서 $a_t$행동을 했을 때(조건부 확률) 그 이후부터 Return의 기댓값이다.
즉 Q는 V보다 한 스텝 앞에서 Return의 기댓값을 구하는 것이다.

수학적으로 정의하면
$V^\pi(s_t)=E[G_t|s_t]=\int_{a_t,...}G_tp(a_t,...)d(a_t,...a_T)$

$Q^\pi(s_t,a_t)E[G_t|s_t,a_t]=\int_{s_{t+1},a_{t+1},...}G_tp(s_{t+1},a_{t+1},...)d(s_{t+1},a_{t+1},...)$

이다. 위에 $\pi$는 특정 정책 $\pi$를 따른다는 것을 의미하고 $\pi$에 따라 가치함수의 값은 달라진다. 위에서 설명했던 것처럼 Q는 V에서 한 스텝 앞에서 Return의 기댓값을 구한 것이기 때문에 V는 Q의 기댓값이라고 정의할 수 있다. (V 입장에서 행동은 확률적이기 때문에)

그러면 V를 Q에 대하여 이렇게 정리할 수 있다.
$V(s)=\sum_{a \in A} \pi(a|s)*Q^\pi(s,a)$
Q역시 V로 정의할 수 있는데 $Q^{\pi}(s,a)$는 특정 상황 s 에서 특정 행동 a를 했기 때문에 Environment에게 Reward를 받는다. 이후 상태천이 행렬로 다음 state가 확률적으로 정해지는데 다음 상태가 정해지면 그 이후는 $V^\pi(next \; state)$로 정의할 수 있다. 즉,$Q^\pi(s,a)=R_s^a+\gamma\sum_{s^* \in S} P_{ss^*}^a V^{\pi}(s^*)$ 로 정리할 수 있다.

$V^\pi(s)=\sum_{a \in A} \pi(a|s)*Q^\pi(s,a)$
$Q^\pi(s,a)=R_s^a+\gamma\sum_{s^* \in S} P_{ss^*}^a V^{\pi}(s^*)$
이 관계식들은 Bellman Equation을 유도할 때 매우 중요한 역할을 하고 이후 강화학습 알고리즘에서도 자주 사용되기 때문에 기억해야 한다.

3 Bellman Equation

Agent의 목표는 Value를 최대화 하는 것이다. 하지만 MDP의 값들이 확률적으로 부여되기 때문에 각 상태에 대한 Value값을 구하는 것을 쉽지 않다. 이것을 해결하기 위해 고전적인 Reinforcement Learning에서는 Dynamic Programming을 이용했는데 그러기 위해 Value function과 Q function을 Recursive 형태로 바꿀 필요가 있다. Value function과 Q function의 Recursive한 형태를 Bellman Equation이라고 부른다. Bellman Equation은 아까 구한 V와Q의 관계식으로 쉽게 유도할 수 있다.

$V^{\pi}(s)=\sum_{a \in A} \pi(a|s)(R_a^s+\gamma \sum_{s^* \in S}P_{ss^*}^aV^\pi(s^*))$
$Q^{\pi}(s,a)=R_s^a + \gamma \sum_{s^* \in S} P_{ss^*}^a \sum_{a^* \in A} \pi(a^*|s^*)Q^\pi(s^*,a^*)$

이 두식을 Bellman Equation이라고 부르며 이것을 이용해 Agent는 상태에 따른 Value값을 구한다.

만약 Agent가 놓인 상황이 Grid World라 Environment의 모든 변수를 파악할 수 있다고 가정하면 (이것을 model-based Reinforcement Learning이라고 한다.)

$V^\pi=R^\pi+\gamma P^\pi V^\pi$
$V^\pi=(1-\gamma P^\pi)^{-1}R^\pi$
이렇게 Value 값을 해석학적으로 구할 수 있다. 하지만 실생활에서는 Environment를 완벽하게 모델링하는 것은 불가능하기 때문에 이런 방식은 사용할 수 없고 신경망으로 근사한다. 저 방법은 Old School Reinforcement Learning이기 때문에 개념 정도만 가볍게 훑고 넘어가자.

4 Optimal Policy

우리는 이제 Bellman Equation을 통해 Value를 구할 수 있다고 가정하자. 우리의 목표는 Value 최대화이기 때문에 현재 얻은 reward를 기반으로 Policy를 지속적으로 수정해 나간다. 바나흐 고정점 정리에 의해 계속 Policy를 수정해 나가면 최대 Value값에 수렴한다. 이것을
최적 정책 정리(Optimial policy theorem)라 부른다.

• 최적 정책 $\pi^*$가 존재하며,모든 존재하는 정책 $\pi$에 대하여 $\pi^* \ge \pi 를 만족한다. (최적 정책의 존재성)$
• 최적 정책들은 $\pi^*$ 최적 상태 가치 함수를 성취한다. 즉, $V_{\pi^*}(s)=V^*(s)$
• 최적 정책들은 $\pi^*$ 최적 행도 가치 함수를 성취한다.
  즉, $Q_{\pi^*}(s,a)=Q^*(s,a)$

정리하면 최적의 정책을 찾으면 우리는 최대 가치 함수를 찾은 것이므로 원래 Agent의 목표인 가치 최대화를 달성할 수 있다. 그러므로 최적 정책을 찾는 것이 바로 강화학습의 핵심이고 그것을 어떻게 찾느냐로 여러 알고리즘이 만들어졌다. (Agent의 핵심은 가치 최대화 강화학습의 핵심은 최적 정책을 찾기)

여러 방식중 가장 고전적인 DQN 방식을 예로 들자면

$\pi^*(a|s)= \begin{cases} 1 & (if \;a=\arg\max_{a \in A}Q^*(s,a)) \\ 0 & (otherwise) \end{cases}​$

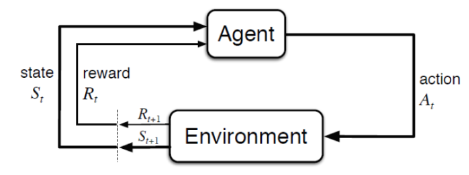
어떤 상태 s에서 선택할 수 있는 $a \in A$에서 가장 큰 Q값을 가진 a를 Action으로 취한다. 이처럼 확률적인 Policy가 아니라 s에따라 a가 구체적으로 정해지는 Policy를 Deterministic Policy라고 하고 DQN,SARSA,DDPG가 Deterministic Policy 계열에 알고리즘이다.

지금까지 MDP Bellman Equation 그리고 Value function Optimal Policy에 대하여 살펴 보았다. 오늘 배운 것을 요약하자면 Agent의 원래 목표는 Return을 최대화 하는 것인데 MDP가 확률적이기 때문에 Return의 기댓값(Value function)을 최대화 하는 것으로 바뀐다. Value를 계산하는 것은 어렵기 때문에 고전적인 Reinforcement Learning에서는 Resursive 형태의 Bellman Equation을 가지고 Dynamic Programming을 이용해 계산한다. Value의 값은 Policy에 따라 달라지는데 가장 큰 Value 함수를 만들어내는 Policy를 Optimal Policy라고 하며 우리가 강화학습을 이용해 찾아야 하는 것이다. 모든 강화학습의 알고리즘은 이 정책을 어떻게 효율적으로 찾느냐에 대하여 다룬다.(Agent는 Maximum Value 개발자는 강화학습을 이용해 Optimal Policy를 찾는다.) 최적 정책을 찾는 가장 고전적인 방식으로 DQN 방식이 있는데 한 상태에서 선택할 수 있는 행동중에 가장 큰 Q값을 가진 a를 Action으로 취한다. 이것을 Deterministic Policy라고 한다.(Deterministic Policy 말고도 Stochastic Policy도 있다. A2C A3C PPO SAC가 이계열의 알고리즘이다.)

Bellman Optimal Equation

Definition

$V^*(s)=\max\limits_{\pi` \in \pi} V^\pi(s)$
$Q^*(s,a)=\max\limits_{\pi` \in \pi} Q^\pi(s,a)$

Bellman Optimal Equation

$V^*(s)=\sum\limits_{s \in S} \pi^*(a|s)Q^*(s,a)=\max\limits_{a \in A(s)}Q^*(s,a)$
$Q^*(s,a)=R_s^a+\gamma\sum\limits_{s` \in S}P_{ss`}^aV^*(s)$

$V^*(s)=\max\limits_{a\in A(s)}(R_s^a+\gamma\sum\limits_{s` \in S}P_{ss`}^aV^*(s))$
$Q^*(s,a)=R_s^a+\gamma\sum\limits_{s` \in S}P_{ss`}^a\max\limits_{a` \in A(s`)}Q^*(s`,a`)$