Union-find algorithm

Union-find algorithm은 공통 원소가 없는 서로소 집합(disjoint set)을 다루기 위한 algorithm이다.
이름 그대로 Union 합집합 연산과 Find 원소의 소속 집합 찾는 연산을 효율적으로 할 수 있다.

Union-find algorithm은 tree 구조를 사용하여 집합들을 관리한다. 같은 tree 내에 있으면 같은 집합에 속해있는 것이고 root node가 같은 원소들은 같은 집합 내에 있다고 말할 수 있다.

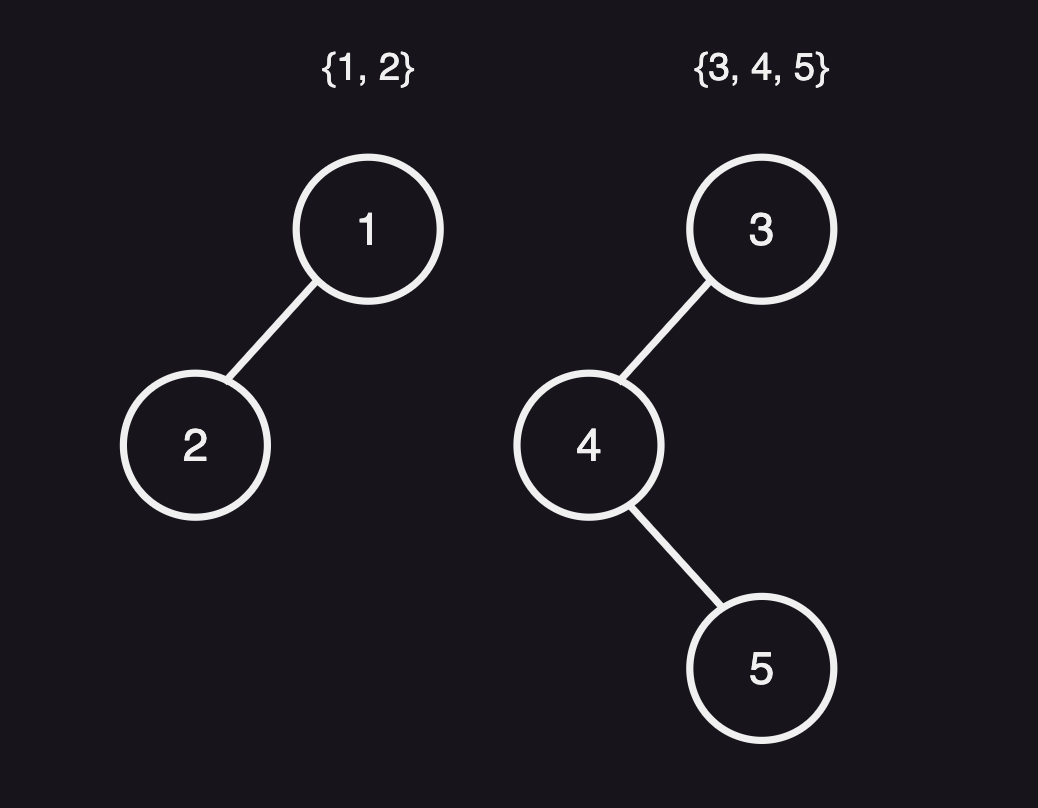
각 원소들은 오직 부모가 누구인지만 알고 있기 때문에 2개의 원소가 같은 집합에 포함된 것인지 판단하기 위해서는 재귀를 사용해 계속 부모를 찾아 올라가야한다.
실제 코드로 어떻게 구현되는지 확인해보자.

1. Algorithm 연산

1. Make set

make_set()은 원소들을 초기화하는 과정으로 각 원소의 부모를 자신으로 설정한다.
Root node 1개만 가지고 있는 tree n개가 만들어졌다.

	def make_set(n):
    	parent = [i for i in range(n + 1)]
        return parent
    
	make_set(5) # 0~5까지의 원소 각각의 부모를 자신으로 설정한다. 이 예시에서 0은 사용하지 않는다.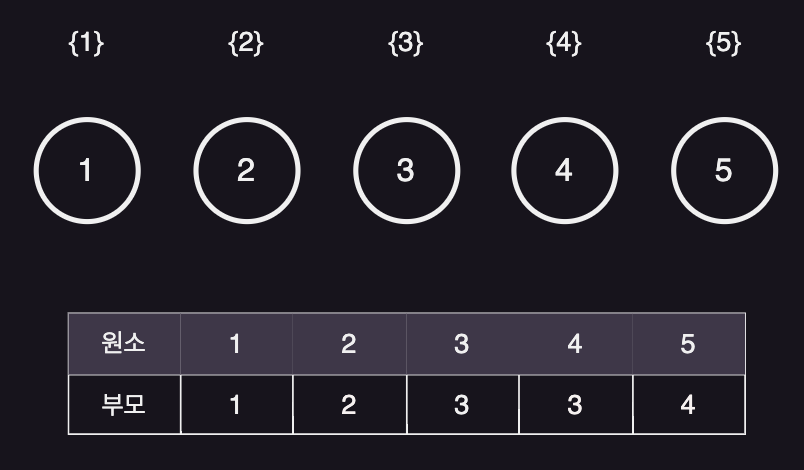

2. Union

union()은 합집합 연산이다. 먼저 x, y 값이 주어질 때 뒤에서 살펴볼 find()를 이용하여 root node를 찾고 root node가 같은 경우는 이미 같은 집합에 속해 있으니 아무 일도 하지 않고 함수를 종료한다.
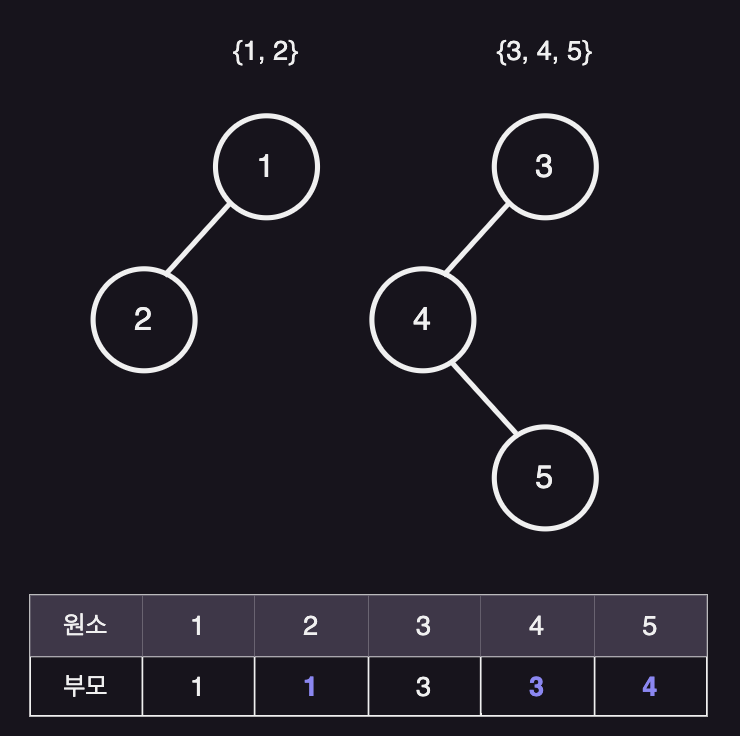
두 원소가 다른 집합에 속해 있을 경우 y의 부모로 x를 설정하면서 두개의 집합이 하나로 합쳐지게 된다.

	def union(x, y):
	    x = find(x)
	    y = find(y)
	    if x == y: # 두 원소의 root node가 같은 경우, 같은 집합에 속해있다.
	        return
	    parent[y] = x
	
    union(1, 2)
    union(3, 4)
    union(4, 5)

3. Find

find() 함수를 이용해 주어진 원소의 root node를 찾을 수 있다.
재귀를 이용해 부모를 찾고 root node를 찾으면 그 값을 return한다.
2와 5가 같은 집합에 있는지 판단 하려면 find(2), find(5)의 값을 비교하면 된다.
find(2)는 1이고, find(5)는 3이므로 각각 다른 집합에 속해있다.

	def find(x):
	    if x == parent[x]:
	        return x
	    return find(parent[x])
    
    find(2) # return 1
    find(5) # return 3
    find(2) != find(5) # 다른 집합에 속해있다.
    find(4) == find(5) # 같은 집합에 속해있다.

2. 시간 복잡도 줄이기

Union-find algorithm이 합집합 연산과 조회 연산에 효율적이지만 추가적인 작업을 통해 시간 복잡도를 더 줄일 수 있다.

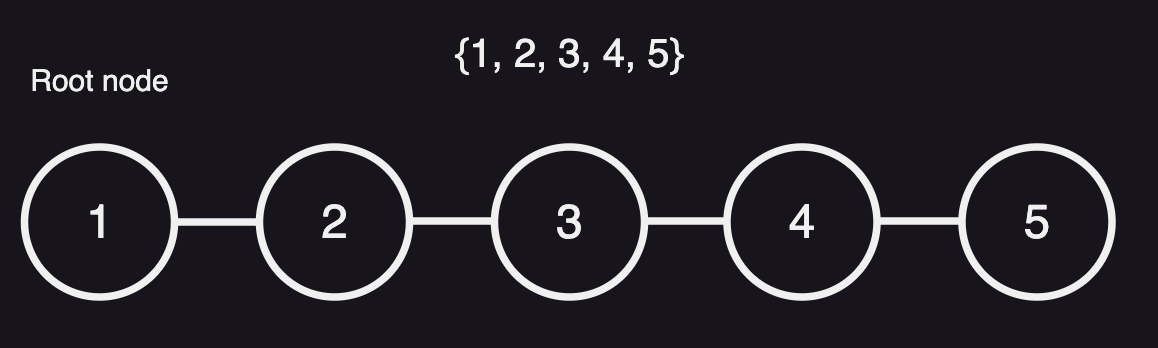
위와 같이 데이터가 선형적으로만 연결된 경우 leaf node인 5의 root node를 찾기 위해 find()를 하면 root node인 1까지 4만큼의 계산이 필요하다. 시간복잡도는 O(n)이 된다.
이때 find()를 하며 경로 압축을 통해 길게 늘어선 node들을 root node에 가깝게 배치할 수 있다.

	def find(x):
	    if x == parent[x]:
	        return x
        parent[x] = find(parent[x]) # x의 root 노드를 x의 parent로 변경한다.
	    return parent[x]

위와 같이 find() 함수 내에서 return 하기 전에 입력 받의 값의 부모를 root node로 업데이트를 한다.

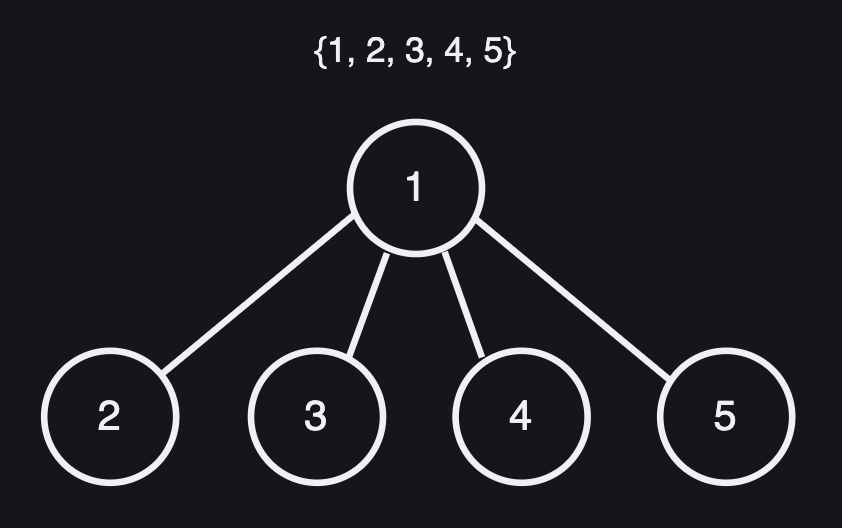
그러면 위의 그림처럼 root node를 찾기 위해 거쳐간 node들은 모두 root node를 부모 노드로 가지게 되고 시간복잡도는 상수에 가까워지게 된다.

3. 전체 코드

total_count = input()

def make_set(n):
    return [i for i in range(n)]

parent = make_set(total_count)

def find(x):
    if x == parent[x]:
        return x
    parent[x] = find(parent[x])
    return parent[x]

def union(x, y):
    x = find(x)
    y = find(y)
    if x == y:
        return
    parent[y] = x