출처
https://programmers.co.kr/learn/courses/30/lessons/42895
Q.
문제 설명
아래와 같이 5와 사칙연산만으로 12를 표현할 수 있습니다.
12 = 5 + 5 + (5 / 5) + (5 / 5)
12 = 55 / 5 + 5 / 5
12 = (55 + 5) / 5
5를 사용한 횟수는 각각 6,5,4 입니다. 그리고 이중 가장 작은 경우는 4입니다.
이처럼 숫자 N과 number가 주어질 때, N과 사칙연산만 사용해서 표현 할 수 있는 방법 중 N 사용횟수의 최솟값을 return 하도록 solution 함수를 작성하세요.
제한사항
N은 1 이상 9 이하입니다.
number는 1 이상 32,000 이하입니다.
수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시합니다.
최솟값이 8보다 크면 -1을 return 합니다.
입출력 예
N number return
5 12 4
2 11 3
일반화
문제의 조건을 일반화하는 방법을 모르겠어서 아래의 방식을 질문하기를 통해 확인 후 다시 작성해보았다.
N을 n번 사용해서 만들 수 있는 수 :
(N을 n번 이어붙인 수) U
(N을 1번 사용했을 때 SET 과 n-1번 사용했을 때 SET을 사칙연산한 수들의 집합) U
(N을 2번 사용했을 때 SET 과 n-2번 사용했을 때 SET을 사칙연산한 수들의 집합) U
... U
(N을 n-1번 사용했을 때 SET 과 1번 사용했을 때 SET을 사칙연산한 수들의 집합)
나의 풀이
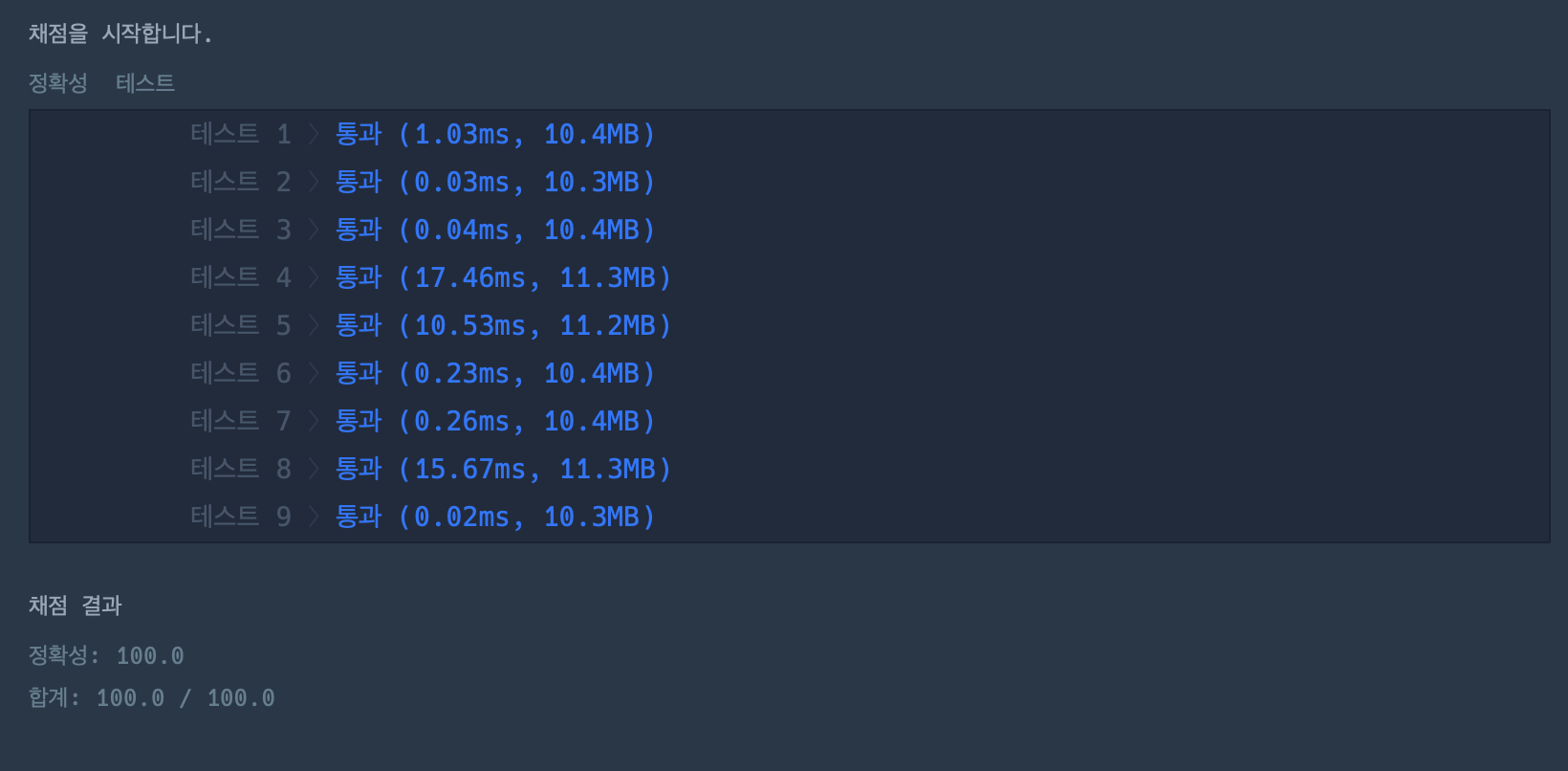
1
def solution(N, number):
answer = -1
numsList = []
for n in range(1, 9): #1개 사용해서 만들 수 있는~8개 사용해서 만들 수 있는
nums = set()
nums.add(int(str(N) * n))
for j in range(1, n-1):
# n개 조합 (1, n-1) (2, n-2),...,,
for op1 in numsList[j]:
for op2 in numsList[-j-1]:
nums.add(op1 + op2)
nums.add(op1 - op2)
nums.add(op1 * op2)
if op2 != 0:
nums.add(op1 // op2)
if number in nums:
answer = n
break
numsList.append(nums)
return answer
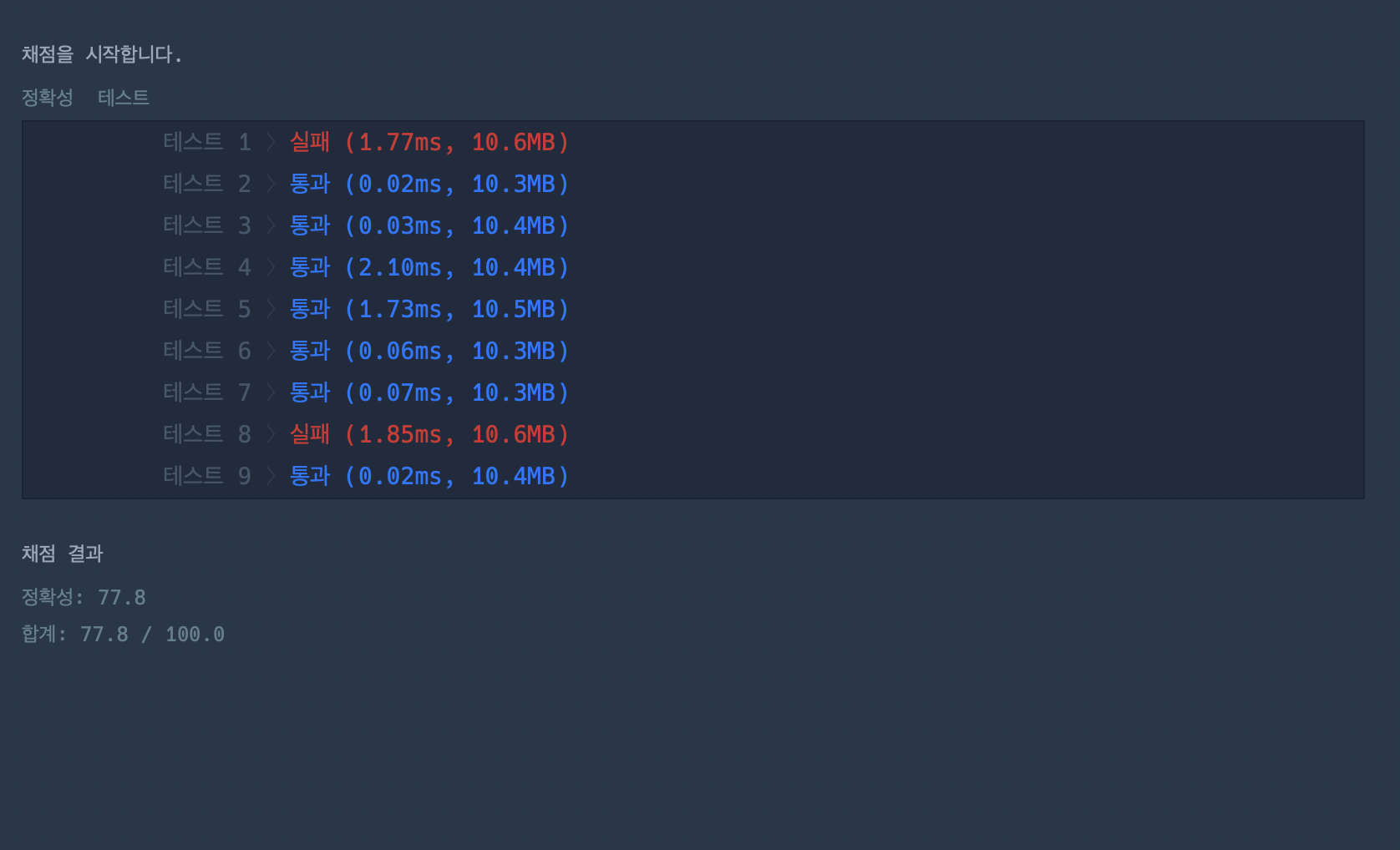
(1, n-1), (2, n-2) 조합만 신경 쓰다가 리스트가 0부터 시작하는데 1로 작성한거를 발견했다. 이를 수정해서 아래와 같이 작성했다.
2 (통과)
def solution(N, number):
answer = -1
numsList = []
for n in range(1, 9): #1개 사용해서 만들 수 있는~8개 사용해서 만들 수 있는
nums = set()
nums.add(int(str(N) * n))
for j in range(0, n-1):
# n개 조합 (1, n-1) (2, n-2),...,,
for op1 in numsList[j]:
for op2 in numsList[-j-1]:
nums.add(op1 + op2)
nums.add(op1 - op2)
nums.add(op1 * op2)
if op2 != 0:
nums.add(op1 // op2)
if number in nums:
answer = n
break
numsList.append(nums)
return answer