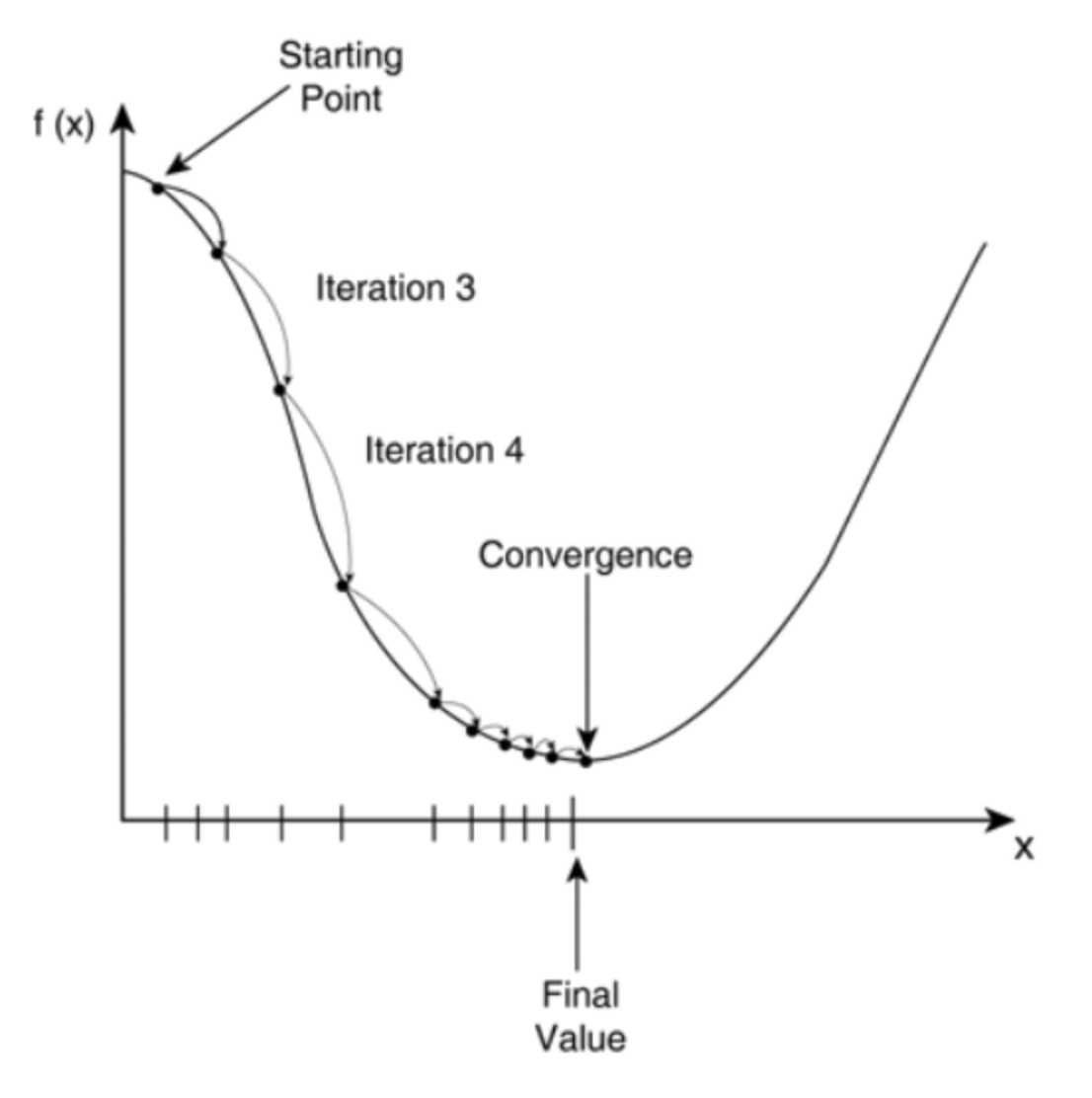
경사 하강법이란?
현재 위치에서 기울기를 따라 목표값을 향하여 계속 낮은 곳으로 반복 이동하는 것을 의미한다.
가상의 키와 몸무게 설정
import tensorflow as tf
_tall = 170
_kg = 70가중치w 와 bias b를 텐서플로우 변수 타입으로 선언.
wValue = tf.Variable(0.1)
bias = tf.Variable(0.1)손실함수 : 가장 최적의 w값과, bias 값을 구하기 위한 함수
def lossFunction():
result = _tall * wValue + bias
# 실제값에서 예측값을 뺀 결과를 리턴한다.
return tf.square(_kg - result)케라스 아담 옵티마이저 사용
# 케라스의 옵티마이저 중 경사하강법을 이용한다. 하강치는 0.1 이다.
opt = tf.keras.optimizers.Adam(learning_rate=0.1)경사에서 가장 낮은 곳까지 이동
for i in range(300) :
# 손실을 최소화하는 부분인데 손실함수와 텐서플로우 변수가 파라미터이다.
opt.minimize(lossFunction, var_list=[wValue,bias])
print(wValue.numpy(),bias.numpy())전체 소스
import tensorflow as tf
_tall = 170
_kg = 70
# 손실함수 : 가장 최적의 a, b 값을 구하기 위한 함수
def lossFunction():
result = _tall * wValue + bias
# 실제값에서 예측값을 뺀 결과를 리턴한다.
return tf.square(_kg - result)
# 가중치w 와 bias b를 텐서플로우 변수 타입으로 선언한다.
wValue = tf.Variable(0.1)
bias = tf.Variable(0.1)
# 케라스의 옵티마이저 중 경사하강법을 이용한다. 하강치는 0.01 이다.
opt = tf.keras.optimizers.Adam(learning_rate=0.01)
# 3000번 돌려서 근사치에 도달할떄까지 경사하강법을 적용한다.
for i in range(3000) :
# 손실을 최소화하는 부분인데 손실함수와 텐서플로우 변수가 파라미터이다.
opt.minimize(lossFunction, var_list=[wValue,bias])
print(wValue.numpy(),bias.numpy())출력 결과
...
...
...
0.4093568 0.40935686
0.40935677 0.40935683
0.4093567 0.40935677
0.40935665 0.4093567
0.40935665 0.4093567
0.40935668 0.40935674
0.4093567 0.40935677
0.40935674 0.4093568
0.40935677 0.40935683
0.40935677 0.40935683
0.40935677 0.40935683검증
(170 * 0.40935677) + 0.40935683 = 70.0000773
이게참...
개념을 잘 모르고(사실은 수학을 모른다가 맞겠지) 덤비려니 어려움이 많다. 반복 학습을 통해 얻어낼 수밖에...
