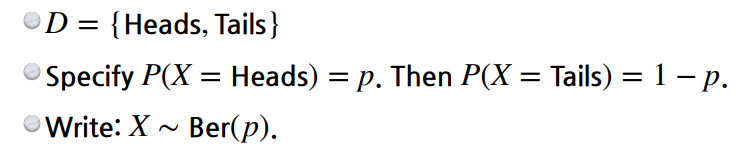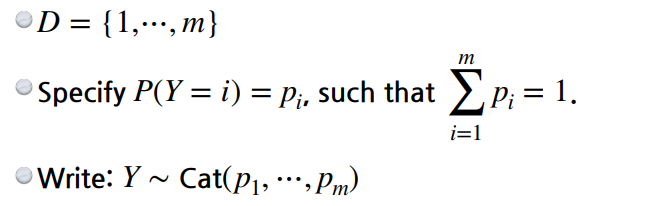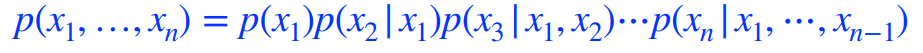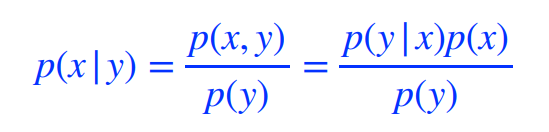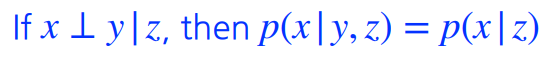1. 오늘 일정

1) 코어타임 전: 수학 스터디 내용 정리

2) 코어타임: Generative Model 학습 및 정리

3) 랜덤 피어세션 & 피어세션

4) 마스터 클래스

5) 수학 스터디

6) 취침

7) 아스날 (개막전) 👍

2. 학습 내용

DL Basic

9강: Generative Models Part 1

Generative Model은 무엇인가?

우리에게 여러가지 개의 이미지가 주어져있다고 가정하자.
우리는 다음과 같은 확률분포 $p(x)$를 알기를 원한다.

• Generation: 개처럼 보이는 $x_{new}$를 위한 확률분포 $x_{new}$ ~ $p(x)$
  • sampling
• Density estimation: $x$가 개같다면 높고, 아니라면 낮은 $p(x)$
  • anomaly detection
• Unsupervised representation learning: 공통점을 가진 부분끼리 묶는것 (예: 귀, 꼬리 등)
  • feature learning

기본적으로 알고 가야할 확률분포
베르누이 분포

카테고리 분포

Auto-regressive Model

Auto-regressive Model이 나오게 된 배경
예시를 통해 알아보자.

위와 같은 binary 이미지에 대해 픽셀이 n개라면, binary이므로 $2^n$개의 상태를 지니게 된다. 따라서 $2^n - 1$의 파라미터를 가지게 된다. 파라미터가 많을수록 학습이 어렵기 때문에 줄여야 한다.

따라서, n개가 각각 독립적이라고 가정하자. 그러면,

• $p(x_1, \dots ,x_n)=p(x_1)p(x_2)\dots p(x_n)$

와 같은 식이 되고 $2^n$의 상태를 가지는데 반해, $n$개의 파라미터를 가지게 되어 파라미터 수가 확 줄어든다. 하지만, 이 독립가정은 비현실적이며 중간에 적당한 부분을 찾아야 한다. 이것이 바로 Conditional Independence이다.

이를 이해하기 위해서는 다음 3가지 규칙을 알아야 한다.

Chain rule

Bayes' rule

Conditional independence

참고로, Conditional independence는 z가 주어졌을 때, x와 y가 독립이므로 y는 상관이 없어지므로 위와 같은 식이 나온다.

그리고 chain rule을 사용하게 되면,

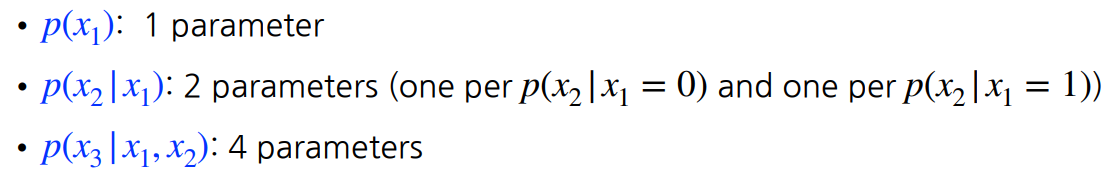
위와 같이 계산이 가능하다.

또한, Markov assumptionn을 가정하면, 파라미터 수가 2n-1임을 알 수가 있다.

이제 Auto-regressive Model에 대하여 알아보자.

28 x 28인 binary 픽셀을 가진다고 가정하면 우리의 목표는 $p(x)=p(x_1, \dots,x_{784})$를 구하는 것이다. 참고로 binary이므로 $x \in \{0,1\}^{784}$가 성립한다.

그리고 chain rule을 통해 $p(x_{1:784}) = p(x_1)p(x_2|x_1)p(x_3|x_{1:2})\cdots$로 표현할 수 있고 이를 autoregressive model이라 한다. 따라서 우리는 모든 확률 변수의 순서가 필요하게 된다.

NADE: Neural Autoregressive Density Estimator

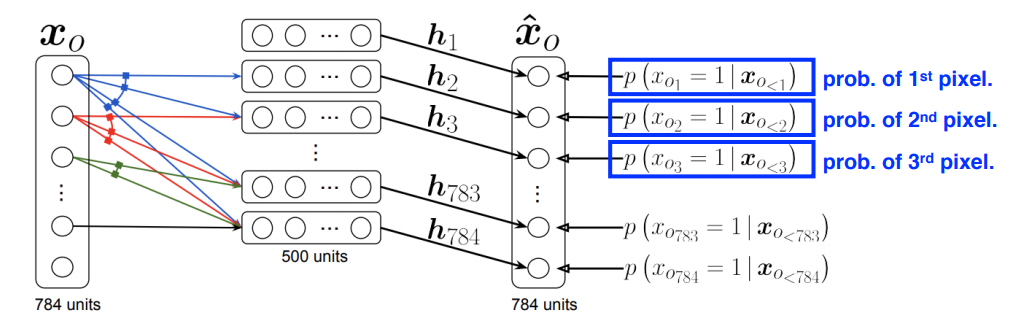
여기서 i번째 픽셀의 확률 분포는 다음과 같다.

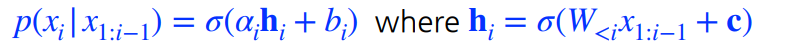
NADE는 확률을 계산하는 explicit모델이고 연속적인 모델에는 가우시안을 적용한다.

Pixel RNN

우리는 RNN 또한 auto-regressive model로 정의할 수 있다.
nxn RGB 이미지에 대해서,

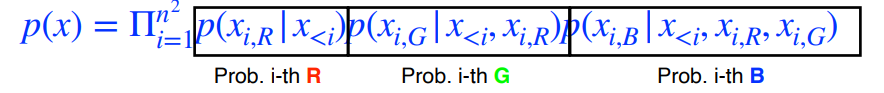
가 성립하고 2가지 모델 구조를 가진다.

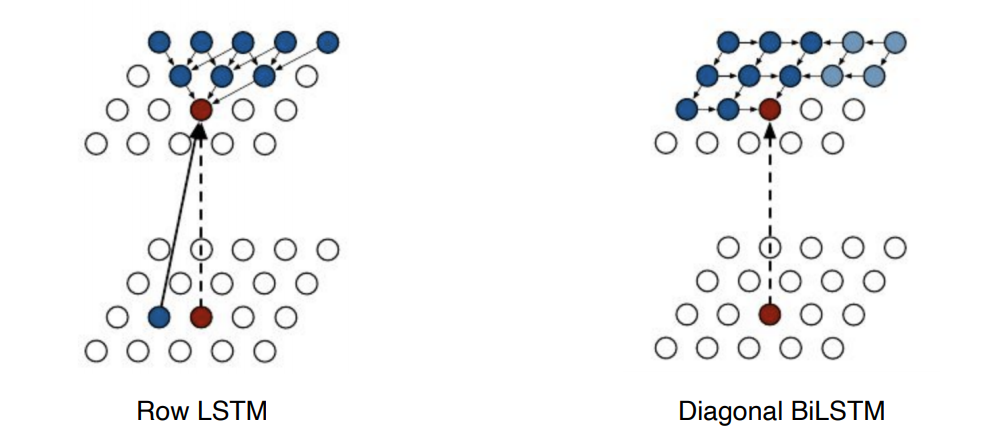
• Row LSTM의 경우, 위를 활용하고 Diagonal BiLSTM은 이전 정보를 활용한다.

10강: Generative Models Part 2

Variational Auto-encoder

posterior distribution은 직접적으로 찾기가 불가능하므로 가장 근사한 variational distribution을 찾는 것이 목적이다.
특히, 우리는 KL divergence를 최소화하는 variational distribution을 찾아야 한다.

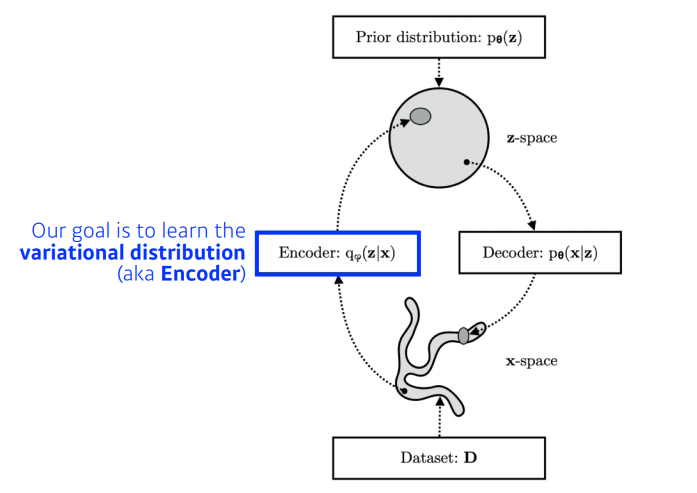
식은 다음과 같다.

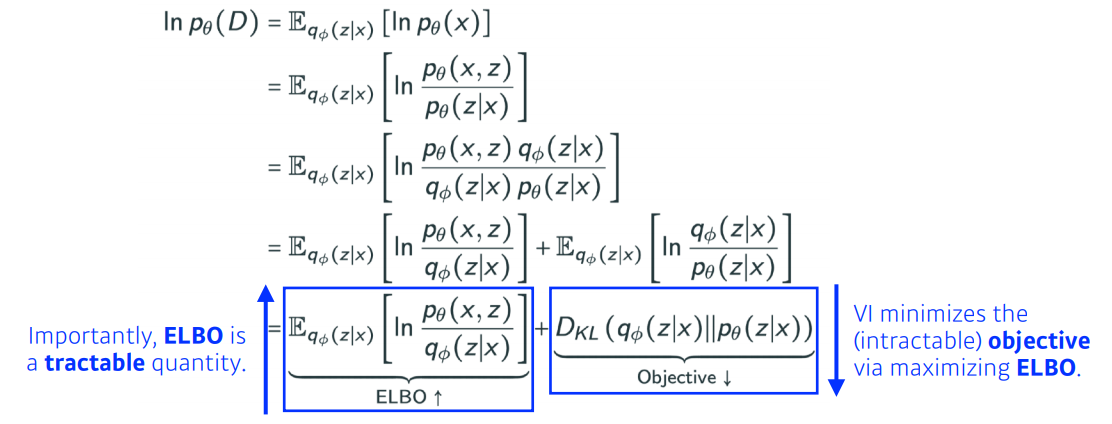
중요한것은 ELBO를 최대화하는 것이고 이를 위해 KL을 최소화해야 한다.

ELBO식은 위와 같이 나타낼 수 있다.

또한, KL의 경우 계산하기 어려워서 isotropic Gaussian을 활용한다. 식은 다음과 같다.

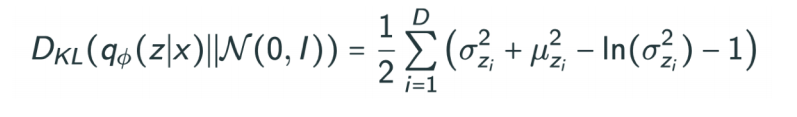
따라서 오직 가우시안만 이용해야하는 KL부분이 단점이라고 볼 수 있다. 따라서 가우시안 대신 GAN을 활용한 Adversarial Auto-encoder도 있다.

GAN (Generative Adversarial Nerwork)

우선 식은 다음과 같다.

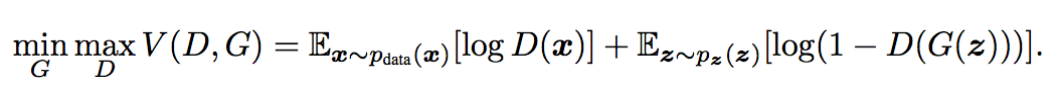
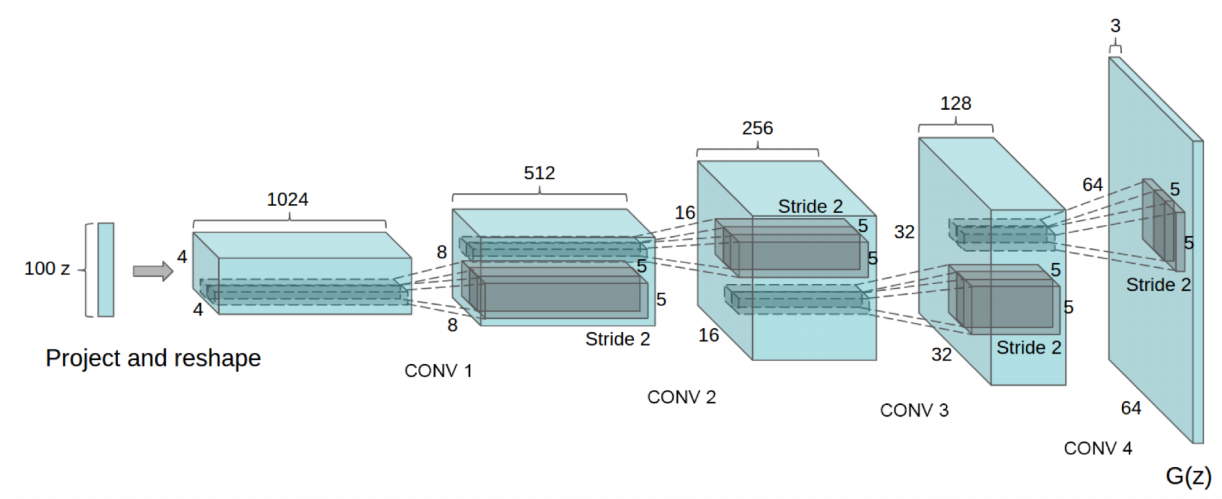
구조는 다음과 같다.

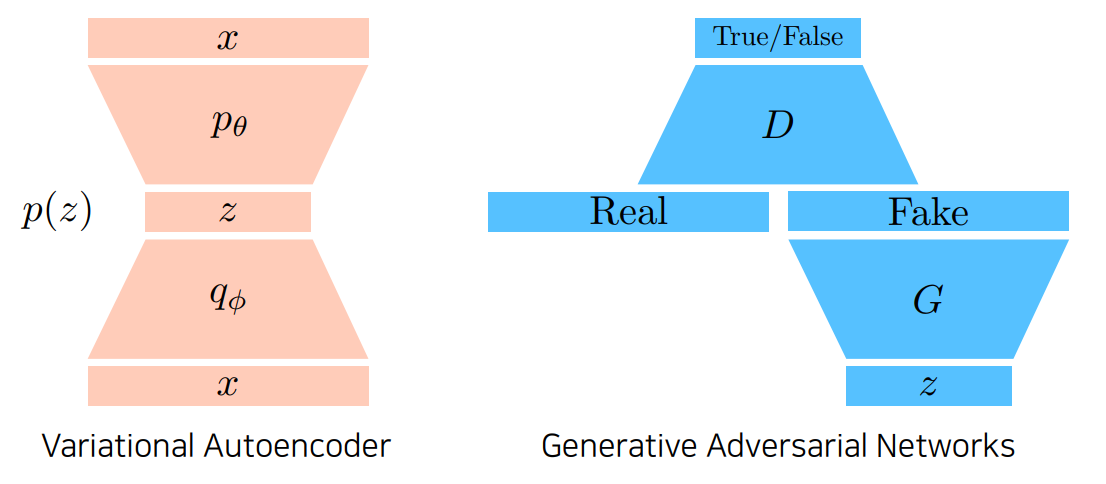
sequential하게 지나가는 VAE와 달리, GAN은 생성하는 G와 판별하는 D를 계속 왔다갔다한다.

GAN은 Generator와 discriminator사이의 minimax game이라고 볼 수 있다.
discriminator입장에서 식을 보면, 다음과 같다.

generator입장에서 식을 보면, 다음과 같다.

다음은 여러가지 GAN의 예시들이다.

DCGAN

Info-GAN

Text2Image

Puzzle-GAN

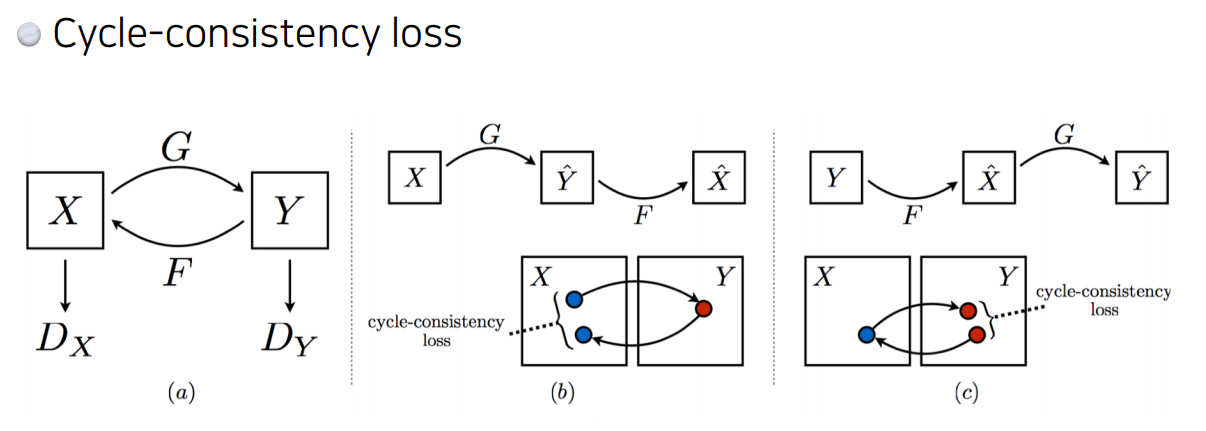
CycleGAN

Star-GAN

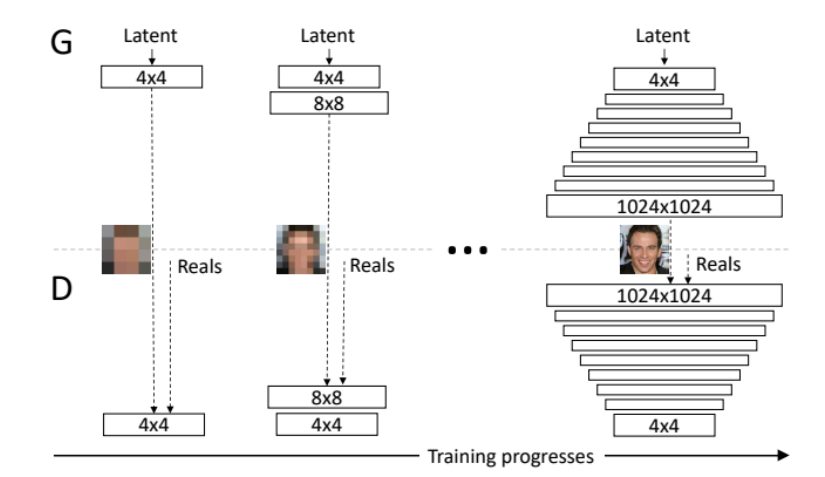
Progressive-GAN

3. 피어 세션 정리

3-1. 랜덤 피어 세션
다른 피어세션 멤버들과 만날 수 있었던 소중한 시간. 다른 팀은 단톡방도 만들었다해서 우리조도 만들어야겠다고 생각함.(바로 실천 👍)
좀 더 자극받는 계기가 됨.

3-2. 피어 세션
오늘 배운 내용 복습 및 멘토링
다음은 멘토링 주요 내용

• 논문 관련
  • 쉬운 논문은 없다.
  • 논문은 2주정도는 걸쳐서 볼 것.
  • 논문은 Top-Tier 학회에서 볼 것.
  • Intro, 모델, experiment 등 각 섹션에서 무얼 말하는지 파악하라
  • 막히는 부분은 레퍼런스로 ㄱㄱ
• 기타
  • 학습 정리하는 시간을 고정하는게 좋다. (시간 관리 차원)
  • 운동하자.

4. 과제 수행 과정

과제는 없었음.

5. 회고

• GAN 관심있었지만 처음 만나니 낯설다. 주말에 논문 좀 볼 것.
• 시각화 공부가 조금 남았으니 주말에..할 것.
• 질문을 좀 잘 안하게 된다.. 질문은 많이 많이 하자.
• 잠도 많이 자고 운동도 하자.

6. 내일 할일

• 아스날 경기보기 ✌
• GAN이나 Transformer 논문 보기
• 잠 보충하기