스물네번째 수업 | 로켓발사 실습 마무리 | 군집화 | Iris 군집화 | 프로야구 타자 군집화

김자영 강사님

로켓발사 실습

모델링

변수 선택

# 독립 변수 X
X = df.drop(['Launched?], axis=1)

# 종속 변수 y
y = df['Launched?']

데이터 분할

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)

모델 생성 및 훈련

from sklearn.tree import DecisionTreeClassifier

model = DecisionTreeClassifier(random_state=42, max_depth=5)
model.fit(X_train, y_train)

분류 모델의 평가지표

pred_test = model.predict(X_test) # 테스트 세트 예측
pred_train = model.predict(X_train) # 훈련 세트 예측

• predict(X_test): 테스트 데이터를 사용해 모델이 예측한 발사 여부 계산
• predict(X_train): 훈련 데이터를 사용해 모델이 예측한 발사 여부 계산

from sklearn.metrics import classification_report

print(f'''test score >>>>>>>>>>
	{classification_report(y_test, pred_test)}''')
print(f'''train score >>>>>>>>>>
	{classification_report(y_train, pred_train)}''')

• classification_report(y_test, pred_test): 테스트 세트에 대한 모델 성능을 평가하는 보고서 출력
• classification_report(y_train, pred_train): 훈련 세트에 대한 성능 평가 출력

# 테스트 세트에 대한 성능
test_accuracy = accuracy_score(y_test, pred_test)
test_precision = precision_score(y_test, pred_test)
test_recall = recall_score(y_test, pred_test)
test_f1_score = f1_score(y_test, pred_test)
test_cm = confusion_matrix(y_test, pred_test)

# 훈련 세트에 대한 성능
train_accuracy = accuracy_score(y_train, pred_train)
train_precision = precision_score(y_train, pred_train)
train_recall = recall_score(y_train, pred_train)
train_f1_score = f1_score(y_train, pred_train)
train_cm = confusion_matrix(y_trian, pred_train)

• accuracy_score: 전체 데이터 중에서 모델이 올바르게 예측한 비율
• precision_score: '발사됨(Y)'으로 예측한 것들 중에서 실제로 발사된 경우의 비율
• recall_score: 실제로 발사된 것들 중에서 모델이 올바르게 발사됨으로 예측한 비율
• f1_score: 정밀도와 재현율의 조화 평균을 계산
• confusion_matrix: 예측값과 실제값의 비교를 통해 혼동행렬 만들기

교차검증

# StratifiedKFold 설정
from sklearn.model_selection import StratifiedKFold, cross_val_score

skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42

# cross_val_score 함수로 교차검증 수행
cross_val_score(model, X_train, y_train, scoring='f1', cv=skf).mean()

cv=skf: Stratified KFold로 데이터를 5등분하여 교차검증 수행

# 모델 최종 학습 및 테스트 세트 평가

model.fit(X_train, y_train)
pred = model.predict(X_test)

from sklearn.metrics import classification_report

print(classification_report(y_test, pred)

모델의 학습 결과

# 결정 트리 시각화
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

plt.figure(figsize=(15, 10)) # 그림 크기 설정
plot_tree(model, feature_names=X.columns, filled=True)
plt.show())

• plot_tree: 결정 트리 모델을 시각화하는 함수
• feature_names=X.columns: 트리의 각 노드에 변수 이름 표시
• filled=True: 노드 색상을 통해 예측된 클래스 비율을 시각적으로 나타냄

# 트리 깊이 확인
model.get_depth()

학습된 트리 모델의 깊이 반환. 깊이가 깊으면 트리가 더 복잡하게 학습한 것으로, 과적합 가능성을 높일 수 있다.

# 특성 중요도 시각화
import seaborn as sns

print(f'특성의 중요도 >>> {model.feature_importances_}')

# 막대 그래프
plt.figure(figsize=(4, 3))
sns.barplot(x=model.feature_importances_, y=X.columns)
plt.show()

• model.feature_importances_: 각 특성의 중요도 반환. 값이 클수록 해당 특성이 예측에 더 많은 영향을 미쳤음을 의미
• sns.barplot: 특성 중요도를 막대 그래프로 시각화. x에 중요도 값, y에 특성 이름을 넣어 그래프를 그린다.

# 특정 특성에 따른 발사 여부 히스토그램
sns.histplot(data=df, x='Wind Speed at Launch Time', hue='Launched?')

• sns.histplot: 히스토그램을 그리는 함수로 x에 분석할 특성을 넣고, hue에 색상으로 구분할 범주형 변수를 넣는다.
• x='Wind Speed at Launch Time: 발사 시점 바람의 속도
• hue='Launched?': 로켓 발사 여부에 따라 바람 속도 분포를 색상으로 구분

# 변수 재선택하여 다시 학습 및 평가
# 사용할 특성(X)에서 특정 변수 제거
X = X.drop(['Wind Speed at Launch Time', 'Temp at Launch Time', 'Crewed or Uncrewed'], axis=1)

• X.drop(...): 지정한 열 제거
• axis=1: 열을 제거하겠다는 의미

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

# 모델 생성 및 훈련
model = DecisionTreeClassifier(random_state=42)

# 모델 학습
model.fit(X_train, y_train)

# 예측
pred_train = model.predict(X_train)
pred_test = model.predict(X_test)

# 평가
print(f'test >> {classification_report(y_test, pred_test)}')
print(confusion_matrix(y_test, pred_test))
print(f'train >> {classification_report(y_train, pred_train)}')

# 모델 학습 결과
# 결정 트리 시각화
from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

plt.figure(figsize=(5, 5))
plot_tree(model, feature_names=X.columns, filled=True)
plt.show()

feature_names=X.columns: 각 노드에 해당 변수 이름 표시 계속 까먹는 부분은 한 번 더 적기

# 특성 중요도 시각화
import seaborn as sns

sns.barplot(y=X.columns, x=model.feature_importances_)

• model.feature_importances_: 모델이 학습한 각 특성의 중요도를 반환. 값이 높을수록 해당 특성이 예측에 더 많은 영향을 미침을 의미!

# 박스플롯 시각화
sns.boxplot(data=df, y='Ave Temp', hue='Launched?')

hue='Launched?': 'Launched?' 변수에 따라 박스를 색상으로 구분하여 시각화

# 트리 깊이 확인
model.get_depth()

이제 와서 시각화

변수 정의

categorical_var = ['Wind Direction', 'Condition']
numeric_var = ['High Temp', 'Low Temp', 'Ave Temp', 'Hist High Temp', 'Hist Low Temp', 'Hist Ave Temp', 'Hist Ave Percipitation', 'Max Wind Speed', 'Visibility']

X['Launched?'] = y

• categorical_var: 범주형 변수 리스트.
• numeric_var: 수치형 변수 리스트.
• X['Launched?'] = y: 원래 데이터프레임 X에 y에 저장되어 있는 값을 Launched?라는 이름의 열으로 추가

수치형 변수 박스 플롯 시각화

plt.figure(figsize=(15, 15))
for i, col in enumerate(numeric_var):
	plt.subplot(3, 3, i+1)
    sns.boxplot(data=X, y=col, hue='Launched?') # 'Launched?'에 따라 색상 구분
    plt.title(col)

• plt.subplot(3, 3, i+1): 3*3 그리드에서 i번째 서브플롯 생성
• plt.title(col): 각 플롯의 제목으로 해당 변수 이름 설정
• 각 변수의 중앙값과 분포 확인, 발사 여부에 따라 값의 차이를 파악할 수 있다.

범주형 변수 카운트 플롯 시각화

plt.figure(figsize=(15, 4))
for i, col in enumerate(categorical_var):
	plt.subplot(1, 2, i+1)
    sns.countplot(data=X, x=col, hue='Launched?')
    plt.title(col)

• plt.subplot(1, 2, i+1): 1*2 그리드에서 i번째 서브플롯 생성
• 각 범주에서 발사 여부의 분포를 확인, 어떤 조건에서 발사가 더 많이 이루어졌는지 볼 수 있다.

군집화

k-means clustering

• 개념: K개의 군집을 미리 정하고, 각 데이터를 가장 가까운 군집에 할당하여 군집을 형성
• 특징
  - 원형 클러스터에 적합
  • 사전에 군집의 개수(K)를 정해야 함
  • 작은 데이터셋에서 잘 작동
  • 군집 중심을 이동시키면서 군집을 최적화
• 평가 방법: Elbow Method, Silhouette Analysis를 통해 적절한 군집 개수를 찾음

데이터 준비

# 필요한 라이브러리 임포트
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 테스트 데이터 생성
from sklearn.datasets import make_blobs
features, targets = make_blobs(n_samples=200,
	n_features=2,
    centers=3,
    cluster_std=0.8,
    random_state=0)

• make_blobs: 데이터를 군집화 테스트에 사용할 수 있도록 가상의 데이터 생성
• n_samples=200: 200개의 데이터 생성
• n_features=2: 2개의 특성(변수)을 가진 데이터 만들기
• centers=3: 3개의 군집 만들기
• cluster_std=0.8: 군집 내 데이터가 퍼져 있는 정도(표준편차)를 0.8로 설정
• random_state=0: 동일한 결과를 재현할 수 있도록 난수 시드 고정

# 생성된 데이터 형태 출력
print(features.shape, targets.shape)

• features: (200, 2) 형태의 200개 데이터와 2개 특성을 가진 배열
• targets: (200,) 형태의 각 데이터가 속한 군집(0, 1, 2 중 하나)을 나타내는 레이블

#DataFrame으로 변환
cluster_df = pd.DataFrame(features, columns=['feature1', 'feature2'])
clsuter_df['target'] = targets

• pd.DataFrame(features, columns=['feature1', 'feature2']): features 데이터를 pandas 데이터프레임으로 변환, feature1, feature2라는 두 개 열로 데이터를 구성
• cluster_df['target'] = targets: 각 데이터가 속한 군집(0, 1, 2)을 target 열에 추가

# 타겟 데이터 빈도수 확인
cluster_df['target'].value_counts()

value_counts(): 각 군집(0, 1, 2)에 속하는 데이터의 개수를 세어준다.

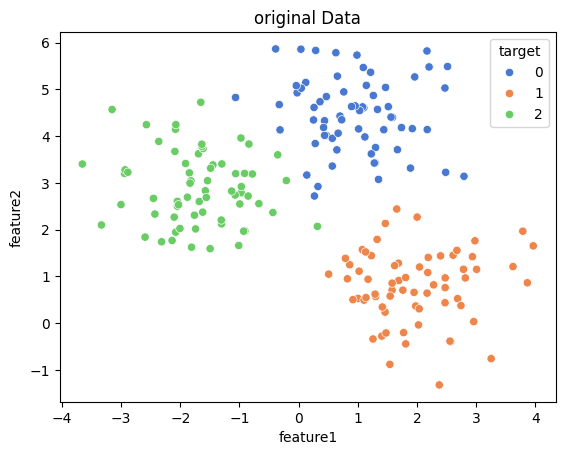
# 데이터 시각화
sns.scatterplot(data=cluster_df, x='feature1', y='feature2', hue='target', palette='muted')
plt.title('original Data')
plt.show()

• sns.scatterplot: seaborn을 이용해 각 데이터 포인트를 군집별로 시각화
• x='feature1', y='feature2: 두 개의 특성(변수)을 각각 x축과 y축에 표시
• hue='target': 각 데이터 포인트를 군집별로 색상을 다르게 표시
• palette='muted': 색상을 약간 부드럽게 표현
  

클러스터링

# KMeans 객체 생성
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3)

• KMeans(n_clusters=3): K-means 알고리즘을 사용해 3개의 군집으로 데이터를 나누는 객체 생성
• n_clusters=3: 3개의 군집을 만들겠다는 의미

# 데이터 학습 및 군집화
kmeans_cluster = km.fit_predict(features)

• fit_predict(): 주어진 데이터를 학습하고 각 데이터가 어느 군집에 속하는지 예측
• fit: 데이터를 학습하여 군집의 중심을 찾는다.
• predict: 각 데이터 포인트를 가장 가까운 군집 중심에 할당
• kmeans_cluster: 각 데이터가 속한 군집의 레이블(0, 1, 2)을 담고 있다.

# 군집 결과를 데이터프레임에 추가
cluster_df['kmeans_cluster'] = kmeans_cluster

kmeans_cluster로 예측한 군집 레이블을 cluster_df에 kmeans_cluster라는 새로운 열로 추가

# 클러스터 중심 확인
km.cluster_centers_

cluster_centers_: 각 군집의 중심 좌표 반환. 이 촤표는 2차원 공간에서 각 군집을 대표하는 중심이다.

# 군집화 결과 시각화
sns.scatterplot(data=cluster_df,
	x='feature1',
    y='feature2',
    hue='kmeans_cluster',
    palette='muted')

hue='kmeans_cluster': 각 군집별로 데이터 포인트의 색상을 다르게 표시

# 군집의 중심 시각화
sns.scatterplot(x=km.cluster_centers_[:,0],
	y=km.cluster_centers_[:,1],
    color='magenta',
    marker='X')

• km.cluster_centers_[:,0], km.cluster_centers_[:,1]: 각 군집 중심의 x, y 좌표를 가져온다.
• marker='X': 각 군집 중심을 X 모양으로 표시
• color='magenta': 군집 중심은 자주색으로 표시

# 그래프 표시
plt.title('k-means Clustering')
plt.show()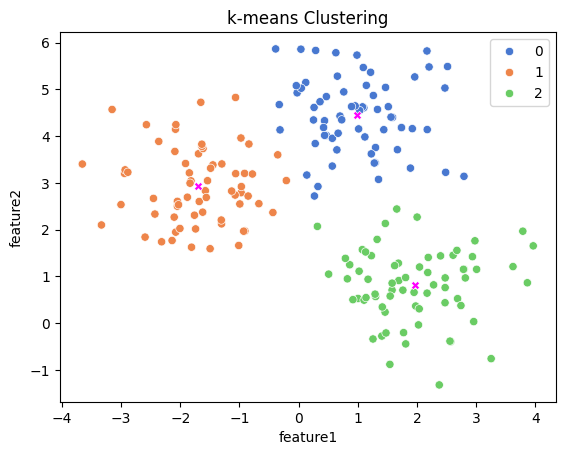

최적의 군집 개수를 구하는 법

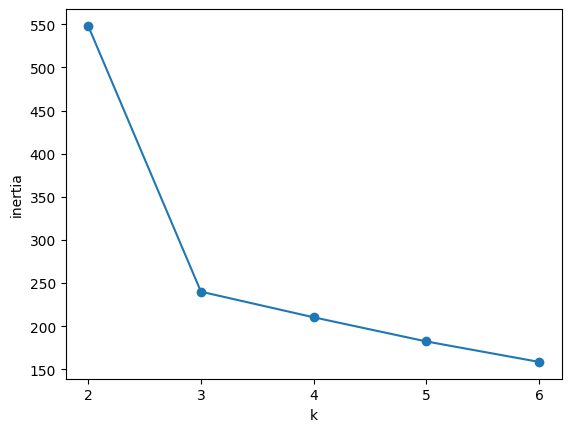
엘보우 방법(Elbow Method) 은 군집의 개수를 늘려가면서 각 군집 내 데이터 포인트들이 중심에 얼마나 가까이 있는지를 측정하는 이너셔(Inertia) 값을 기반으로 한다. 이너셔는 클러스터 중심과 데이터 포인트들 사이 거리의 제곱합을 나타내며, 군집 내 데이터들이 얼마나 밀집되어 있는지 보여준다.

# 이너셔(Inertia) 계산
inertia = []
for n in range(2,7):
	km = KMeans(n_clusters=n)
    inertia.append(km.inertia_)
    
# 이너셔 값을 시각화
plt.plot(range(2, 7), inertia, marker='o')
plt.xlabel('k')
plt.ylabel('Inertia')
plt.show()

• 그래프에서 이너셔 값이 급격히 줄어드는 구간이 있다. 이 구간 이후 이너셔 값이 더이상 급격하게 줄어들지 않으면 그 구간의 K값을 최적의 군집 개수로 선택한다.
• 그래프 모양이 팔꿈치처럼 꺾이는 지점에서 K를 결정하기 때문에 이 방법을 엘보우 방법이라고 부른다.
  

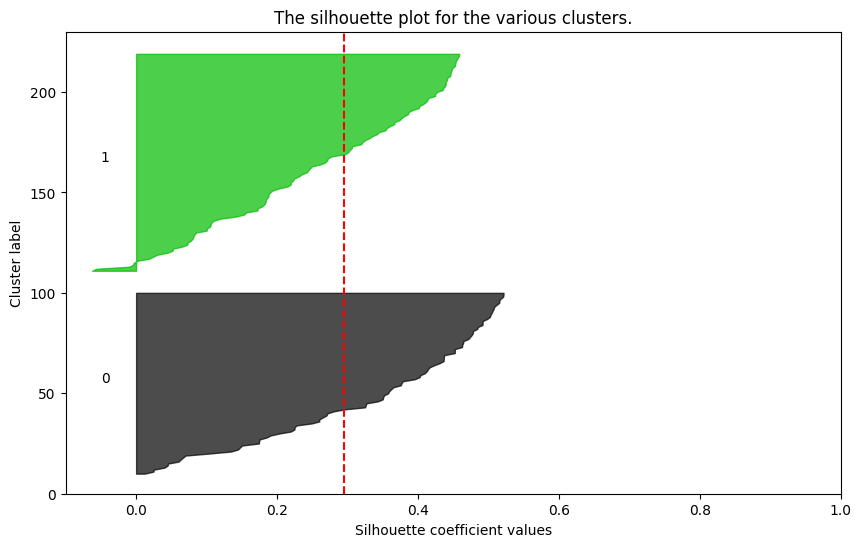
실루엣 분석(Silhouette Analysis)

실루엣 분석은 군집화가 얼마나 잘 되었는지 평가하는 지표인 실루엣 계수(Silhouette Coefficient) 를 사용한다. 각 데이터 포인트가 자신이 속한 군집 내에서 얼마나 잘 묶여 있는지와 다른 군집과는 얼마나 잘 분리되어 있는지를 측정한다.

• 실루엣 계수는 -1에서 1 사이의 값을 가진다.
• 1에 가까울수록 해당 데이터가 올바르게 군집에 속해 있고, 다른 군집과 잘 분리되어 있다는 의미이다.
• 0에 가까우면 군집이 불분명하다는 의미이고, 음수이면 데이터가 잘못된 군집에 할당되었음을 나타낸다.

# 개별 실루엣 계수 계산
from sklearn.metrics import silhouette_samples
cluster_df['silhouette'] = silhouette_samples(features, kmeans_cluster)

• silhouette_samples: 각 데이터 포인트에 대한 실루엣 계수 계산
• cluster_df에 silhouette 열을 추가하여 각 데이터 포인트의 실루엣 계수 확인

# 잘못 할당된 데이터 확인
cond = cluster_df['silhouette'] < 0
cluster_df.loc[cond]

• cluster_df['silhouette'] < 0: 실루엣 계수가 0보다 작은 데이터(다른 군집에 잘못 할당된 데이터)를 찾는다.
• cluster_df.loc[cond]: cond가 True인 행만 선택한다. (잘못된 군집에 할당된 데이터만 반환한다.)

# 평균 실루엣 계수 계산
from sklearn.metrics import silhouette_score
silhouette_score(features, kmeans_cluster)

silhouette_score: 전체 군집화의 품질을 평가하는 평균 실루엣 계수를 계산

# 실루엣 분석 시각화 함수
import silhouette_analysis as s
for k in range(2, 7):
	s.silhouette_plot(features, k)

silhouette_plot(features, k): 실루엣 분석을 시각화하는 함수. 다양한 군집 개수(K)에 대해 군집화 결과를 실루엣 그래프로 시각화하여 최적의 군집 개수를 찾을 수 있다. 강사님이 주신 모듈 안에 들어있던 함수

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)

DBSCAN은 밀도 기반 군집화 알고리즘으로 데이터가 밀집된 영역을 군집으로 인식한다.
1. Epsilon(ε): 한 점을 중심으로 하는 반경의 크기.
2. MinPts: 이 반경 내에 포함되어야 할 최소 데이터 포인트 수.

• Core Point: ε반경 내에 MinPts 이상 포인트가 포함된 데이터 포인트.
• Border Point: Core Point 반경 내에 있지만 자신은 MinPts를 만족하지 못하는 포인트.
• Noise Point: Core Point도 Border Point도 아닌 포인트. (군집에 속하지 않는 데이터)

DBSCAN은 불규칙한 모양의 군집을 탐지하고 이상치(노이즈) 를 잘 식별하는 장점이 있다.

1. 임의의 포인트 선택
2. ε 반경 내 이웃 찾기
3. Core Point 확인: 반경 ε 내의 이웃 수가 MinPts 이상이면 해당 포인트는 Core Point로 간주된다.
4. 군집 확장
5. 반복 과정: 군집에 포함되지 못한 포인트는 Noise로 분류된다.

• 장점
  - 클러스터 개수 사전 지정 불필요
  • 불규칙한 모양의 클러스터 탐지
  • 이상치(Noise) 처리: 데이터 내에 이상치나 노이즈가 포함되어 있어도 DBSCAN은 이를 잘 감지하고 따로 분류해준다.
• 한계
  - 밀도 차이가 큰 클러스터 처리의 어려움: DBSCAN은 모든 클러스터에 동일한 밀도 기준을 적용하므로 밀도가 서로 다른 클러스터를 처리하는 데 한계가 있다.
  • 고차원 데이터에서 성능 저하
  • 파라미터 선택의 민감성: DBSCAN의 결과는 ε과 MinPts 값에 매우 민감하다.
• DBSCAN 선택 이유
  - 이상치가 있는 대규모 데이터셋: DBSCAN은 데이터에서 이상치를 감지하고 군집에 포함시키지 않는 특징이 있다.
  • 불규칙한 모양의 클러스터: 데이터의 클러스터가 비선형적이거나 복잡한 형태를 띌 경우 DBSCAN은 다른 알고리즘보다 유리하다.
  • 클러스터 개수를 알기 어려운 경우: DBSCAN은 클러스터의 개수를 미리 설정할 필요가 없기 때문에 클러스터의 수를 정확히 알 수 없을 때 유리하다.

# 데이터 생성
from sklearn.datasets import make_circles

X, y = make_circles(n_samples=1000, shuffle=True, noise=0.05, random_state=0, factor=0.5)

• make_circles: Scikit-learn의 함수로, 두 개의 동심원(circle) 형태의 2D 데이터를 생성한다.
• n_samples=1000: 총 1000개의 샘플(포인트)을 생성.
• shuffle=True: 데이터를 무작위로 섞는다.
• noise=0.05: 원형 데이터를 약간의 노이즈를 추가해 비선형적으로 만든다.
• factor=0.5: 작은 원과 큰 원의 크기 비율을 설정. factor=0.5는 작은 원의 반지름이 큰 원의 절반임을 의미한다.
• X: 생성된 데이터 포인트 (각각 feature1과 feature2로 이뤄진 2차원 좌표값)
• y: 각 데이터 포인트가 속하는 클래스(0 또는 1).

# 데이터프레임 생성
df = pd.DataFrame(X, columns=['feature1', 'feature2'])
df['target'] = y

# 데이터 시각화
sns.scatterplot(data=df, x='feature1', y='feature2', hue='target', palette='muted')
plt.show()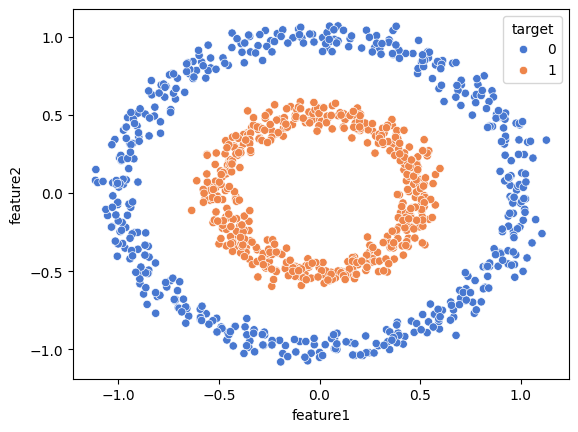

# K-means 클러스터링
from sklearn.cluster import KMeans
km = KMeans(n_clusters=2)
df['kmeans'] = km.fit_predict(X)

• KMeans(n_clusters=2): K-means 알고리즘을 사용해 데이터에서 2개의 클러스터를 찾는다.
• km.fit_predict(X): K-means 알고리즘을 학습하고 각 데이터 포인트가 어느 군집에 속하는지 예측
• df['kmeans'] = km.fit_predict(X): 예측된 군집 번호를 데이터프레임 df에 새로운 열 'kmeans'로 추가하여 각 데이터 포인트가 속한 클러스터를 기록

# 데이터 시각화
sns.scatterplot(df, x='feature1', y='feature2', hue='kmeans', palette='muted')

• Seaborn 라이브러리의 scatterplot을 이용하여 feature1과 feature2 값을 기준으로 데이터 포인트를 그린다.
• hue='kmeans': K-means에 의해 예측된 클러스터 번호(kmeans 열에 저장된 값)에 따라 색상을 다르게 지정

# 클러스터 중심 시각화
sns.scatterplot(x=km.cluster_centers_[:,0], y=km.cluster_centers_[:,1],
	marker='D', color='magenta')

• km.cluster_centers_: K-means 알고리즘이 찾은 두 군집의 중심 좌표 반환
• km.cluster_centers_[:,0], km.cluster_centers_[:,1]: 두 군집의 중심 좌표에서 각각 x와 y 값을 추출
• marker='D': 클러스터 중심을 다이아몬드(D) 모양으로 표시

# 플롯 타이틀 추가 및 그래프 출력
plt.title('k-means clustering')
plt.show()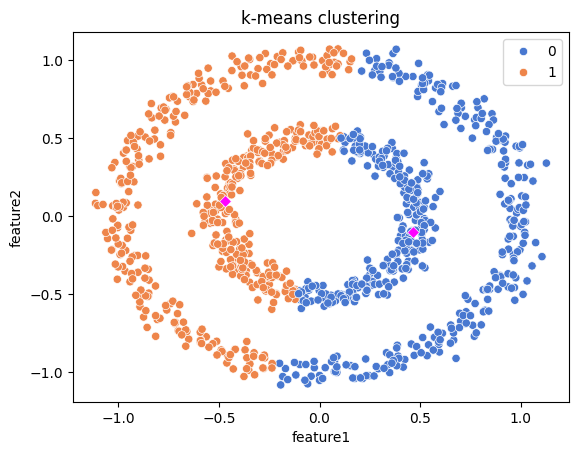

# DBSCAN 클러스터링
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=10)
df['dbscan'] = dbscan.fit_predict(X)

• eps=0.2: 각 데이터 포인트를 중심으로 탐색할 반경(입실론, ε)을 설정. 이 반경 내에 다른 포인트들이 있으면 군집이 형성된다.
• min_samples=10: 각 데이터 포인트가 Core Point로 간주되려면 반경 eps 내에 최소 10개의 이웃이 있어야 한다.
• dbscan.fit_predict(X): DBSCAN 알고리즘을 X 데이터에 적용하여 각 데이터 포인트가 어느 군집에 속하는지 또는 이상치인지 예측한다. 군집에 속하지 않는 이상치 포인트는 -1로 표시된다.
• df['dbscan'] = dbscan.fit_predict(X): 예측된 군집 번호 또는 노이즈 정보를 데이터프레임 df에 'dbscan'이라는 새 열로 추가하여 저장

# 데이터 시각화
sns.scatterplot(df, x='feature1', y='feature2', hue='dbscan')

hue=dbscan: DBSCAN에 의해 예측된 군집 번호 혹은 노이즈 값에 따라 색상을 다르게 지정. 군집에 속한 포인트는 각 군집마다 다른 색상으로 나타나며 노이즈(-1) 로 분류된 포인트는 별도의 색상으로 구분된다.

# 그래프 타이틀 추가 및 출력
plt.title('DBSCAN')
plt.show()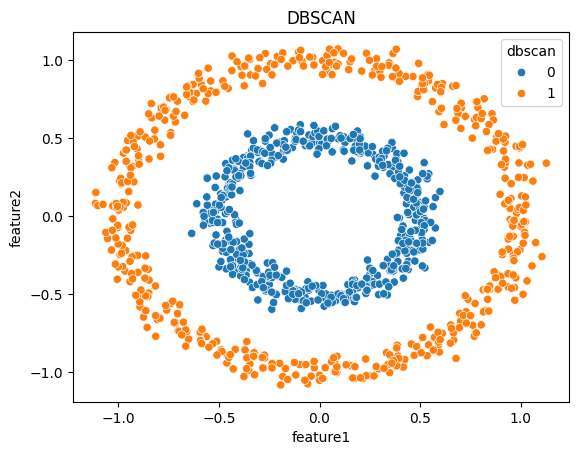

Iris 군집화

데이터 준비

라이브러리 불러오기

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

Iris 데이터셋 로딩

from sklearn.datasets import load_iris

붓꽃 데이터셋 로딩 및 데이터프레임 변환

iris = load_iris()
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names)
df_iris['species'] = iris.target

• iris = load_iris(): 붓꽃 데이터를 로딩하여 변수 iris에 저장. 이 데이터셋은 iris.data와 iris.target으로 구성된다.
• pd.DataFrame(iris.data, columns=iris.feature_names): iris.data는 붓꽃 데이터의 특성 값들이며, 이를 판다스 데이터프레임으로 변환. feature_names는 각각의 특성 이름.
• df_iris['species'] = iris.target: 데이터프레임에 'species' 라는 새로운 열 추가. 여기에는 붓꽃의 종을 나타내는 타겟 값(0, 1, 2) 이 저장된다. 이 값은 각각 Setosa(0), Versicolor(1), Virginica(2) 로 구분된다.

샘플 데이터 출력

df_iris.sample(3)

데이터프레임에서 임의의 3개의 샘플 데이터를 출력하여 데이터를 미리 확인할 수 있다.

k-means clustering

엘보우 기법

# K-means 클러스터링 및 이너셔(Inertia) 계산
from sklearn.cluster import KMeans
inertia = []
for n in range(2, 7):
	km = KMeans(n_clusters=n)
    km.fit(iris.data)
    print(km.inertia_)
    inertia.append(km.inertia_)

• KMeans(n_clusters=n): K-means 알고리즘에서 n_clusters를 n으로 설정하여 n개의 클러스터로 데이터를 군집화. 여기서 n은 2부터 6까지 반복된다.
• km.fit(iris.data): Iris 데이터셋을 이용해 K-Means 모델을 학습시킨다.
• km.inertia_: 이너셔(Inertia) 는 군집 내 데이터포인트들이 군집의 중심(centroid)과 얼마나 가까운지 나타내는 값이다. 이너셔 값이 작을수록 각 군집의 중심으로 데이터가 더 밀집해 있음을 의미한다. 이 값은 클러스터 내 데이터 포인트 간의 거리 제곱합으로 계산된다.

# 엘보우 기법 그래프 시각화
plt.plot(range(2, 7), inertia, marker='o')
plt.xticks(range(2, 7))
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()

• plt.plot(range(2, 7), inertia, marker='o'): x축에 클러스터 개수 k, y축에 이너셔 값을 대응시킨 엘보우 그래프를 그린다. marker='o'는 데이터 포인트를 원형 마커로 표시한다.
• plt.xticks(range(2, 7)): x축 값(클러스터 개수)을 2에서 6까지 표시
• plt.xlabel('k'), plt.ylabel('inertia'): x축에는 클러스터 개수 k, y축에는 이너셔 값을 라벨로 표시
  

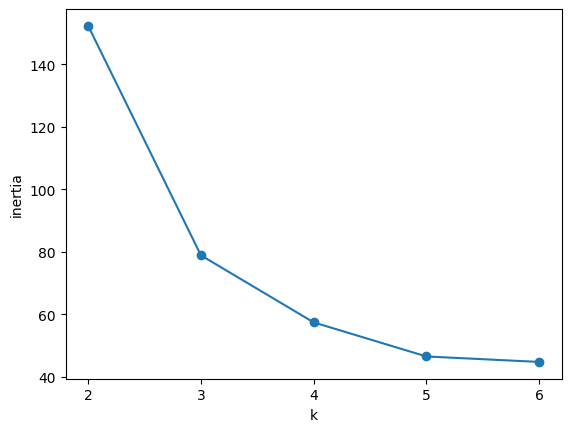
실루엣 분석

for k in range(2, 5):
	s.silhoette_plot(iris.data, k)

위에서 사용했던 silhouette_analysis 모듈을 사용하여 실루엣 분석을 진행. 주어진 데이터 iris.data에 대해 클러스터 수를 2부터 4까지 바꾸면서 실루엣 점수를 계산, 그 결과를 시각화한다.

K-means 클러스터링

km = KMeans(n_clusters=3)
df_iris['kmeans'] = km.fit_predict(iris.data)
df_iris.sample(3)

# 클러스터링 결과 확인
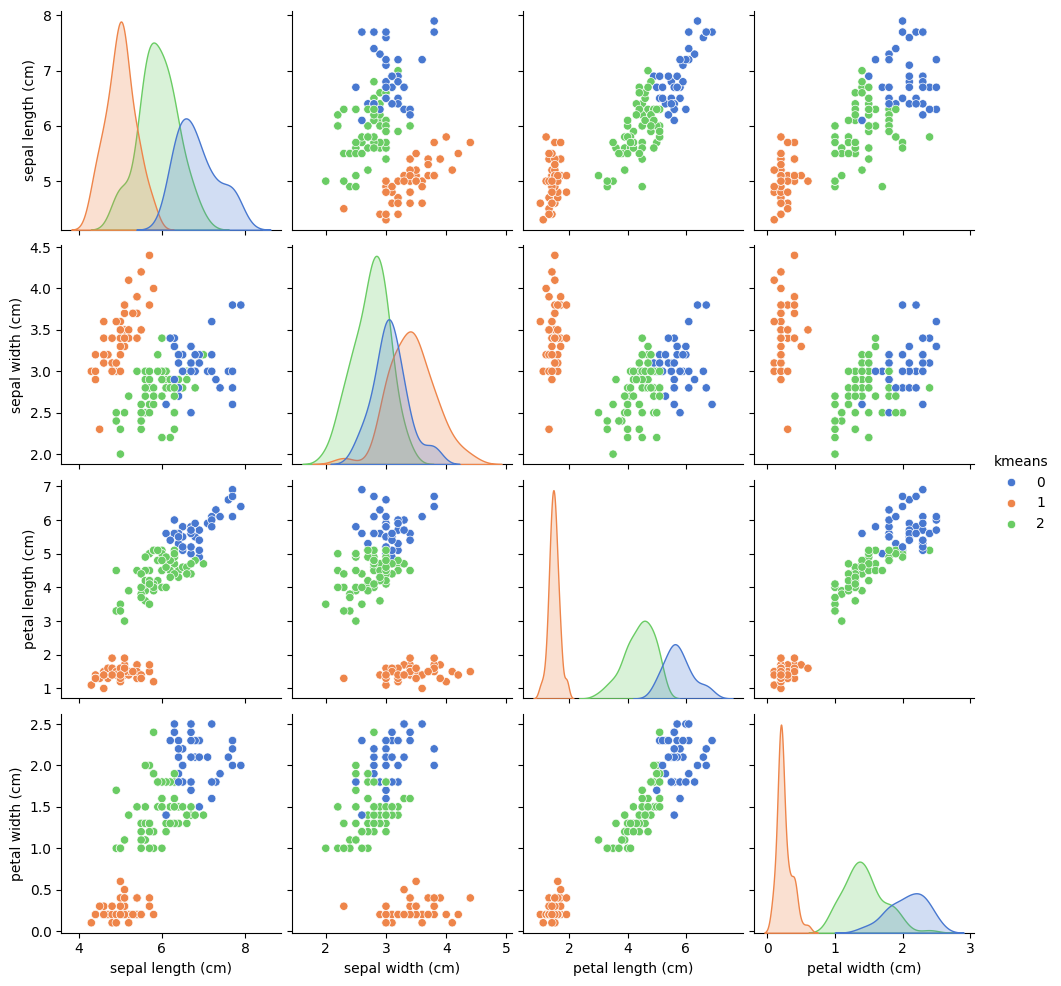
df_iris[['species', 'kmeans']].value_counts()

• 군집화 결과와 실제 species 데이터를 비교하여 각 클러스터에 할당된 데이터 개수를 확인한다.
• 실제 라벨과 K-means 결과가 얼마나 일치하는지 평가

# 시각화
df = df_iris.iloc[:,[0,1,2,3,5]]
sns.pairplot(df, hue='kmeans', palette='muted')

df_iris에서 필요한 열들(특성 4개와 K-means 결과)을 선택, pairplot을 그린다.

DBSCAN

from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.8, min_samples=5)
df_iris['dbscan'] = dbscan.fit_predict(iris.data)

• eps=0.8: 반경, 각 데이터 포인트 주변에 이 거리 내에 최소한 min_samples=5개의 데이터가 있어야 같은 클러스터로 묶인다.
• fit_predict(): 데이터를 학습, 클러스터 할당 결과를 반환. 결과는 df_iris의 dbscan 열에 저장된다.

# 클러스터링 결과 출력
display(df_iris.sample(3))
print(df_iris['dbscan'].value_counts())

• df_iris['dbscan'].value_counts(): 각 클러스터에 할당된 데이터 포인트의 수를 출력
• -1: 노이즈 포인트

# DBSCAN 결과 시각화
df = df_iris.iloc[:,[0,1,2,3,6]]
sns.pairplot(df, hue='dbscan', palette='muted')
plt.show()

• df_iris에서 4개의 특성과 DBSCAN 결과를 확인하여 pairplot을 그린다.
• hue='dbscan'으로 각 클러스터를 서로 다른 색으로 구분하여 시각화
• Pairplot을 통해 특성 간 관계에서 DBSCAN이 클러스터를 어떻게 형성했고, 노이즈 포인트가 어떻게 구분되는지 확인할 수 있다.

프로야구 타자 군집화

데이터 준비

라이브러리 불러오기

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

np.set_printoptions(suppress=True, precision=8)

• np.set_printoptions: 출력될 배열이나 숫자 형식을 지정
• suppress=True: 지수 표기법 억제
• precision=8: 소수점 이하 8자리까지 숫자를 표시하도록 설정

데이터 불러오기

# CSV 파일 불러오기
hitter1 = pd.read_csv('https://github주소')
hitter2 = "
hitter3 = "

github 주소로도 데이터를 불러올 수 있다는 걸 강사님 통해서 배웠다.
이 실습에서 배운 건 아니고, 전에 언제 실습에서 배웠는데,, 기억 안남.

# 데이터 크기 확인
print(f'hitter1 >>> {hitter1.shape}')
print(f'hitter2 >>> {hitter2.shape}')
print(f'hitter3 >>> {hitter3.shape}')

• shape 속성은 데이터의 행(row)과 열(column) 개수를 나타낸다.
• hitter1.shape: hitter1 데이터 프레임의 행과 열 수를 알려준다.

테이블 병합

hitter_concat = pd.concat([hitter1, hitter2, hitter3], ignore_index=True)

• pd.concat(): 여러 데이터프레임을 세로로 연결(병합)하는 함수
• 리스트 [] 안에 합치고자 하는 데이터프레임들을 순서대로 넣는다.
  ignore_index=True: 기존 인덱스를 무시, 새로운 연속적인 인덱스를 부여

변수 선택

X = hitter_concat[['OPS', 'ISO', ..., 'XR']]
y = hitter_concat['YrPlayer']

데이터 스케일링

# StandardScaler 임포트 및 객체 생성
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()

• StandardScaler: sklearn에서 제공하는 표준화 도구
• scaler = StandardScaler(): StandardScaler 객체 생성

scaler = StandardScaler()처럼 객체를 미리 생성하는 이유는 코드의 유연성과 재사용성을 높이고 여러 번 사용할 수 있도록 하기 위함이다. (출처: ChatGPT)

# 데이터 변환
X.loc[:, 'OPS':'XR'] = scaler.fit_transform(X)

• X.loc[:, 'OPS':'XR']: loc를 사용해 X 데이터 프레임에서 OPS부터 XR까지의 열을 선택. 이 열들을 스케일링 대상으로 설정.
• fit_transform(X): StandardScaler의 fit_transform() 메소드를 사용해 데이터를 표준화
  - fit: 데이터의 평균과 표준편차를 계산
  • transform: 이를 이용해 각 열의 값을 표준화

k-means clustering

엘보우 기법

# 라이브러리 임포트
from sklearn.cluster import KMeans

# 클러스터 개수별 KMeans 실행 및 관성 값 저장
inertia = []
for n in range(2,7):
	km = KMeans(n_clusters=n)
    km.fit(X)
    print(km.inertia_)
    inertia.append(km.inertia_)

• inertia = []: 관성 값을 저장할 빈 리스트
• for n in range(2,7): 클러스터 개수 k를 2부터 6까지 변경하면서 K-평균을 반복 실행
  - n_clusters=n: k-means의 클러스터 개수 설정
  - km.fit(X): 선택한 클러스터 개수로 데이터 X에 KMeans 모델을 학습시킨다.
  • km.inertia_: 관성 값을 반환. 관성 값이 클수록 클러스터 내 데이터 점들이 멀리 퍼져 있다는 뜻.

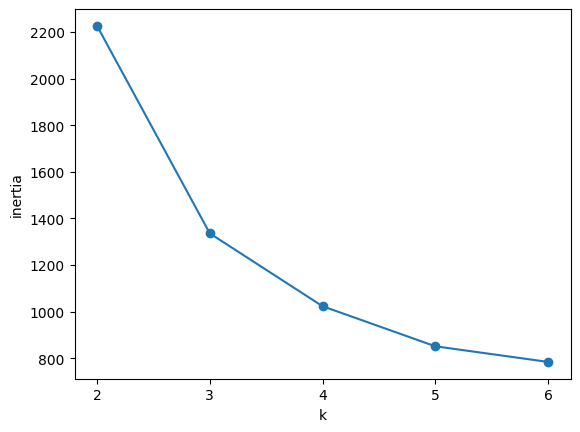
# 엘보우 그래프 그리기
plt.plot(range(2,7), inertia, marker='o')
plt.xticks(range(2,7))
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()

• plt.plot(range(2,7), inertia, marker='o': k 값(2~6) 을 x축에, 관성 값을 y축에 두고 선 그래프 를 그린다. marker='o'는 각 점을 동그라미로 표시.
• plt.xticks(range(2,7)): x축의 눈금을 2부터 6까지 설정
• plt.xlabel('k'), plt.ylabel('inertia'): x축 레이블을 'k', y축 레이블을 'inertia'로 설정
  

군집화

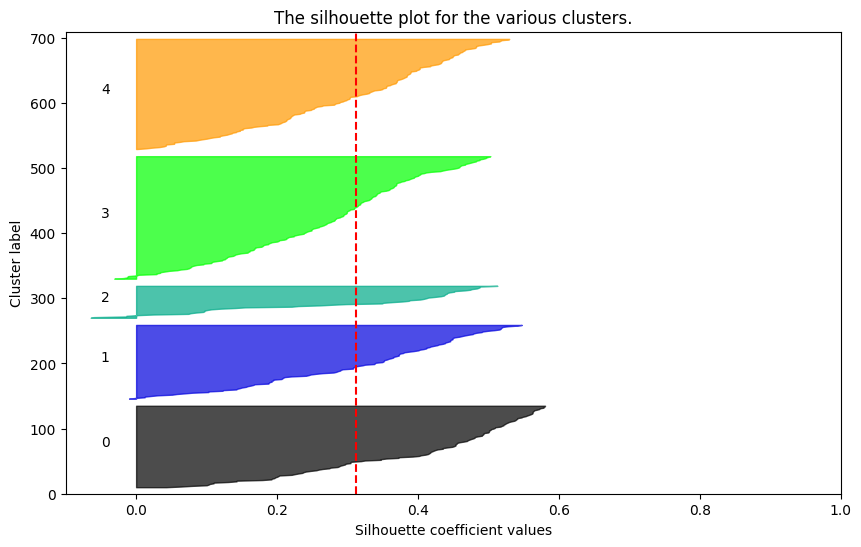
# 실루엣 분석을 통한 최적의 k 찾기
import silhouette_analysis as s
for k in range(2,6):
	s.silhouette_plot(X, k)

강사님께서 주신 silhouette_analysis 모듈 사용.

# k-means clustering
from sklearn.cluster import KMeans
km = KMeans(n_clusters=4, random_state=42)
kmeans_cluster = km.fit_predict(X)
kmeans_cluster

• n_clusters=4: 실루엣 분석 결과에서 k=4가 적합하다고 판단되어 4개의 클러스터로 설정.
• km.fit_predict(X): KMeans 객체의 fit_predict() 메소드를 사용해 X 데이터를 학습시키고 각 데이터가 속하는 클러스터 레이블을 예측
• 결과는 kmeans_cluster 변수에 저장되며 이는 데이터가 속하는 클러스터 번호를 나타낸다.

군집화 결과 분석

df = pd.DataFrame(X, columns=X.columns)
df['kmeans_cluster'] = kmeans_cluster
df.head()

• pd.DataFrame(X, columns=X.columns): 표준화된 데이터 X를 사용하여 새로운 데이터 프레임 df를 생성. X.columns는 원래의 열 이름을 유지.
• df[kmeans_cluster'] = kmeans_cluster: 클러스터링 결과(kmeans_cluster)를 데이터프레임 df에 추가.

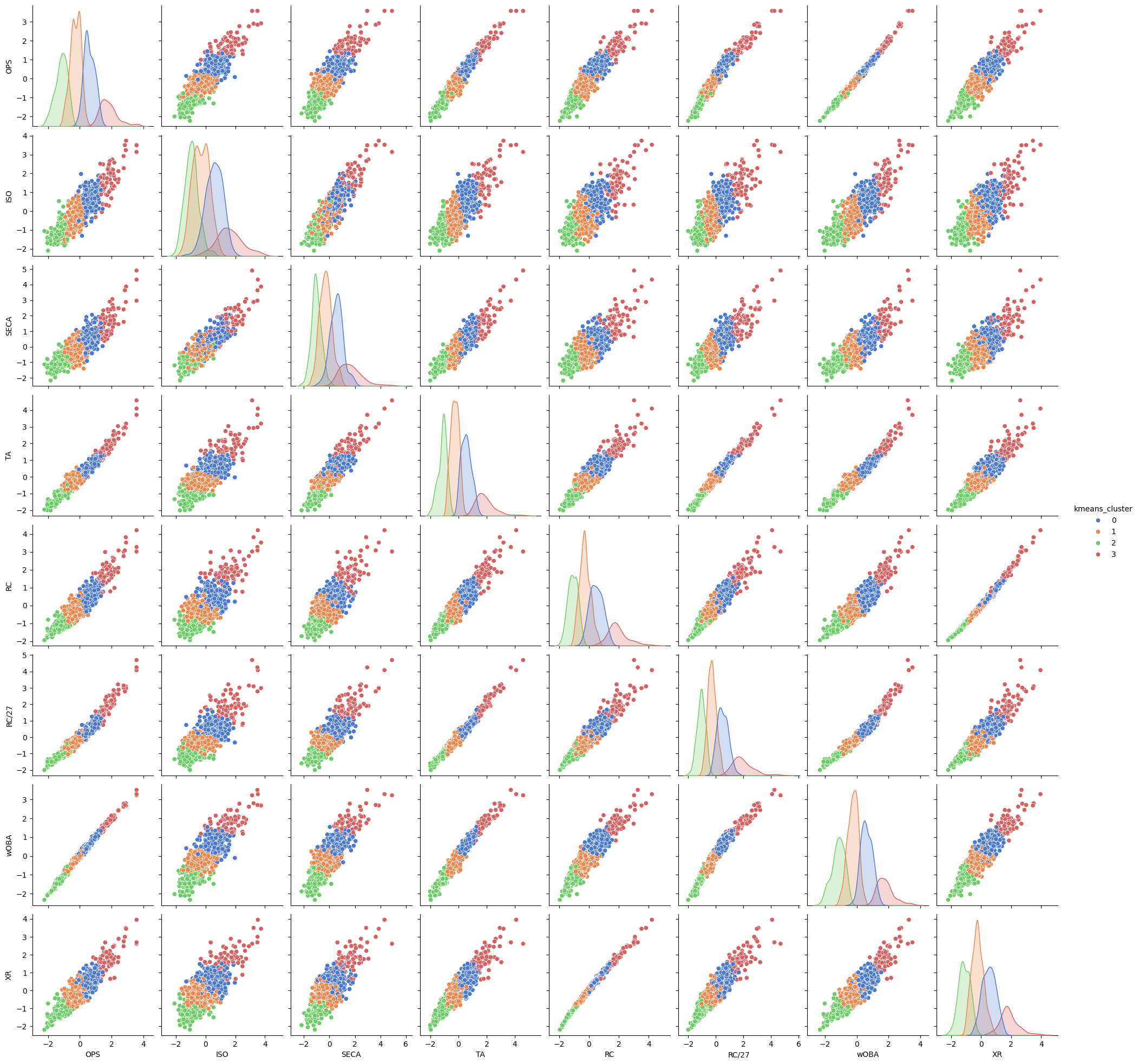
# pairplot을 사용한 시각화
sns.pairplot(df, hue='kmeans_cluster', palette='muted')
plt.show()

• sns.pairplot(): Seaborn의 pairplot 함수는 여러 변수 간의 쌍변수 관계를 그려주는 함수이다. 즉 각 변수들의 2D 산점도를 만들어 데이터의 분포를 시각화한다.
  설명이 위와 반복되는 것 같은 느낌이 든다면 사실일 것이다. 오늘의 나에게 어제의 내가 글작성을 미뤄두었기 때문이지..
  

# 변수 선택
cols = df.columns[:-1]

df.columns[:-1]: 데이터프레임 df에서 마지막 열(kmeans_cluster)을 제외한 나머지 열들을 선택. 즉 클러스터링에 사용된 X만 대상으로 시각화 준비.

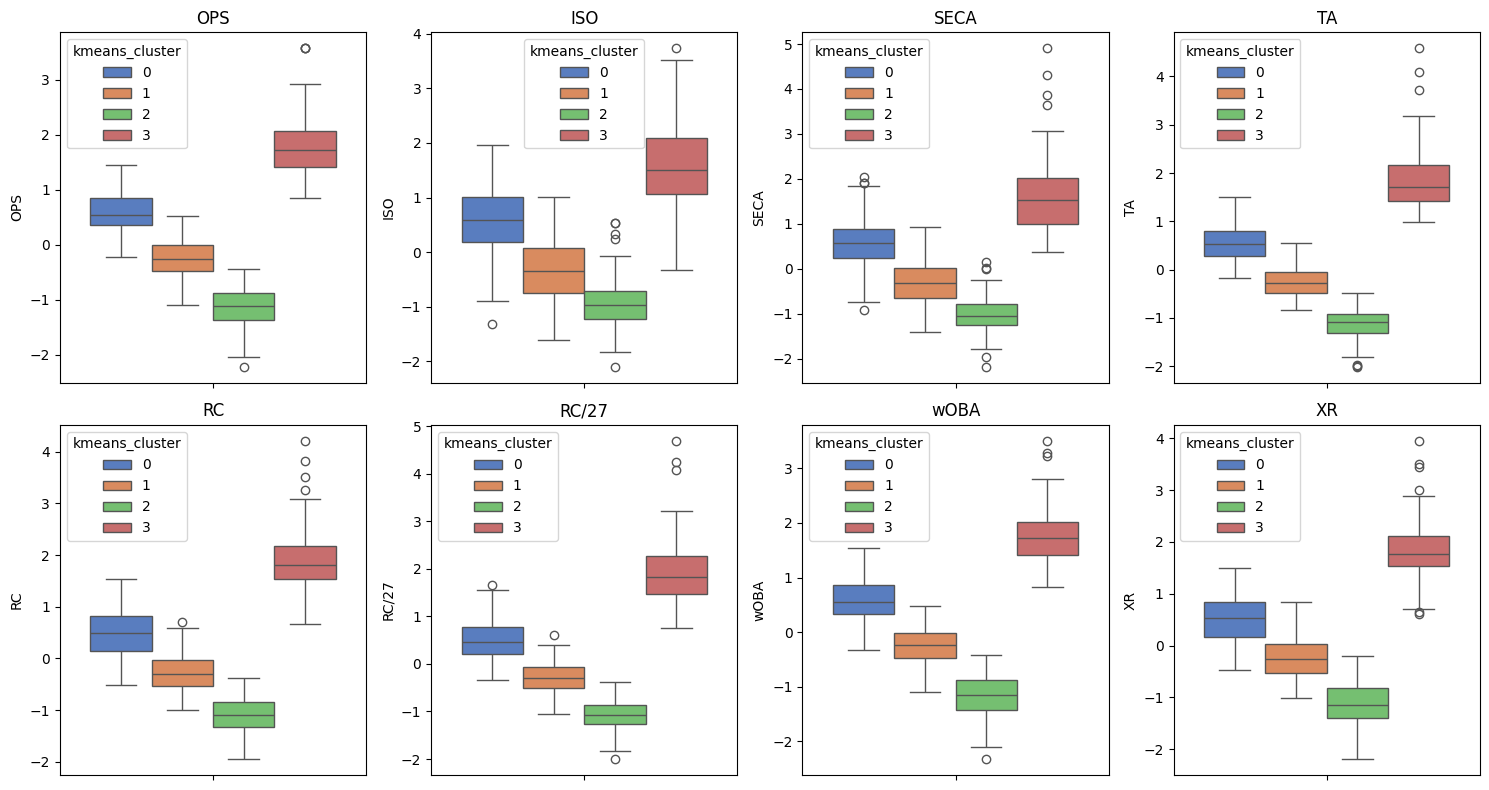
# 박스플롯 그리기
plt.figure(figsize=(15,8))
for i, col in enumerate(cols):
	plt.subplot(2,4,i+1)
    sns.boxplot(data=df, y=col, hue='kmeans_cluster', palette='muted')
    plt.title(col)
plt.tight_layout()

• for i, col in enumerate(cols): cols에 포함된 각 변수에 대해 반복적으로 박스플롯을 그린다.
• plt.subplot(2,4,i+1): 한 화면에 2행 4열의 서브플롯을 그리고, i+1번째 위치에 해당 변수의 박스플롯을 그린다.
• plt.tight_layout(): 그래프 간 간격을 자동 조정하여 겹치지 않고 보기 좋게 배치되도록 한다.
  

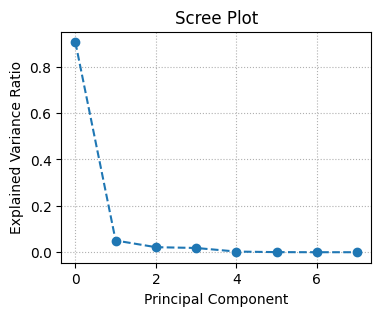
주성분 분석

주성분 선택

# 주성분 계산
from sklearn.decomposition import PCA
pca = PCA()
principal_components = pca.fit_transform(X)
printcipal_components.shape

• from sklearn.decomposition import PCA: scikit-learn 라이브러리에서 PCA 모듈을 가져온다.
• pca = PCA(): PCA 객체 생성. 기본적으로 모든 주성분을 계산하도록 설정된다.
• principal_components = pca.fit_transform(X): 데이터 X에 대해 PCA를 수행하여 주성분을 계산
  - fit_transform: PCA를 적용(fit) 하고 변환(transfrom) 하여 주성분을 반환

# 컬럼별 설명된 분산 비율 확인
explained_variance = pca.explained_variance_ratio_

explained_variance = pca.explained_variance_ratio_: 각 주성분이 설명하는 분산 비율을 저장. 이 값은 각 주성분이 데이터의 전체 변동성을 얼마나 설명하는지 나타낸다. (explained_variance[0]: 첫번째 주성분이 설명하는 분산 비율)

# 누적 분산 확인
cumulative_variance = explained_variance.cumsum()

cumulative_variance = explained_variance.cumsum(): 각 주성분의 설명된 분산 비율의 누적 합 계산. 이를 통해 몇 개의 주성분을 사용해야 전체 변동성의 몇 %를 설명할 수 있는지 알 수 있다. (cumulative_variance[2]: 첫번째, 두번째, 세번째 주성분이 합쳐서 설명하는 변동성을 나타낸다.)

# screeplot 그리기
plt.figure(figsize=(4,3))
plt.plot(explained_variance, marker='o', ls='--')
plt.xlabel('Principal Component')
plt.title('Scree Plot')
plt.ylabel('Explained Variance Ratio')
plt.gird(ls=':')
plt.show()

• ls='--': 선을 점선으로 설정
• plt.grid(ls=':'): 그래프에 점선 그리드 추가
  

주성분 추출

# 2개의 주성분 추출
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
principal_components = pca.fit_transform(X)

pca = PCA(n_components=2): PCA 객체를 생성하면서 추출할 주성분의 개수를 2로 설정.

# 데이터프레임 생성
df_pca = pd.DataFrame(principal_components, columns=['pca1', 'pca2'])

추출된 주성분을 사용하여 새로운 데이터 프레임 df_pca 생성

k-means clustering

엘보우 기법

from sklearn.cluster import KMeans

# 최적의 k 찾기
inertia = []
for k in range(2, 7):
	kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(df_pca)
    inertia.append(kmeans.inertia_)

• kmeans = KMeans(n_clusters=k, random_state=42): 클러스터 수를 k로 설정하여 KMeans 객체를 생성.
• kmeans.fit(df_pca): PCA로 변환된 데이터프레임 df_pca에 k-means clustering을 적합시킨다. 클러스터 중심이 계산된다.
• inertia.append(kmeans.inertia_): 현재 k 값에 대한 관성을 리스트 inertia에 추가.

# 결과 시각화
`plt.figure(figsize=(5, 4))
plt.plot(range(2, 7), inertia, marker='o')
plt.xticks(range(2, 7))
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()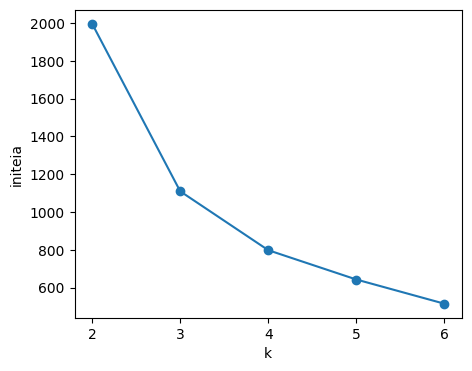

군집화

# k-means clustering
kmeans = KMeans(n_clusters=4, random_state=42)
df_pca['pca_cluster'] = kmeans.fit_predict(df_pca)

• kmeans = KMeans(n_clusters=4, random_state=42): 클러스터 수를 4로 설정하여 KMeans 객체 생성
• df_pca['pca_cluster'] = kmeans.fit_predict(df_pca): PCA로 변환된 데이터프레임 df_pca에 k-means clustering을 적용하여 각 데이터 포인트가 속하는 클러스터를 예측, 그 결과를 'pca_cluster'라는 새로운 열에 저장.

# 군집 결과 시각화
sns.scatterplot(data=df_pca, x='pca1', y='pca2', hue='pca_cluster', palette='muted')

• x='pca1', y='pca2': x축과 y축에 각각 첫번째 주성분과 두번째 주성분을 사용
• hue='pca_cluster': 데이터 포인트 색상을 클러스터 레이블에 따라 다르게 표시
  

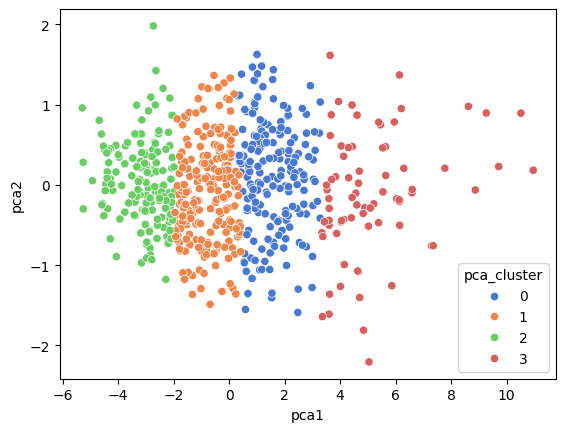
# 원본 데이터프레임에 군집 정보 추가
df['pca_cluster'] = df_pca['pca_cluster']

PCA 클러스터 레이블을 원본 데이터프레임 df에 새로운 열 'pca_cluster'로 추가

# 클러스터 값의 빈도수 확인
df[['kmeans_cluster', 'pca_cluster']].value_counts()

원본 데이터프레임 df에서 'kmeans_cluster'와 'pca_cluster' 두 열의 조합에 대한 빈도 수를 계산. >> 각 군집의 조합 개수를 보여준다.

실루엣 분석

데이터프레임 생성

df['player'] = y

개별 데이터 실루엣 계수

from sklearn.metrics import silhouette_samples
df['silhouette'] = silhouette_samples(X, kmeans_cluster)

• from sklearn.metrics import silhouette_samples: scikit-kearn 라이브러리에서 실루엣 계수를 계산하는 함수를 가져온다.
• df['silhouette'] = silhouette_samples(X, kmeanscluster): 각 데이터 포인트에 대해 실루엣 계수를 계산하고 그 결과를 데이터프레임 df에 새로운 열 'silhouette'로 추가. 실루엣 계수는 -1에서 1 사이의 값을 가지고, 값이 클수록 해당 데이터 포인트가 클러스터 내에 잘 속해 있다는 것을 의미.

# 클러스터 별 중심 선수 찾기
max_idx = df.groupby('kmeans_cluster')['silhouette'].idxmax()
df.loc[max_idx]

• max_idx = df.groupby('kmeans_cluster')['silhouette'].idxmax(): 각 클러스터에 대해 실루엣 계수가 가장 큰 데이터 포인트의 인덱스를 찾는다. groupby 메소드를 사용하여 클러스터별로 데이터를 그룹화하고, idxmax()로 각 그룹의 최댓값을 가진 인덱스를 가져온다.
• df.loc[max_idx]: 최댓값 인덱스를 사용하여 해당 선수 정보를 출력한다. 이는 클러스터에서 실루엣 계수가 가장 높은 선수(해당 클러스터에 제일 적합한 선수)를 나타낸다.

# 클러스터별 주변 선수 찾기
min_idx = df.groupby('kmeans_cluster')['silhouette'].idxmin()
df.loc[min_idx]

• min_idx = df.groupby('kmeans_cluster')['silhouette'].idxmin(): 각 클러스터에 대해 실루엣 계수가 가장 작은 데이터 포인트의 인덱스를 찾는다. idxmin() 함수를 사용, 각 그룹의 최소값을 가진 인덱스를 가져온다.
• df.loc[min_idx]: 최소값 인덱스를 사용하여 해당 선수의 정보를 출력. 이는 각 클러스터에서 실루엣 계수가 가장 낮은 선수(해당 클러스터에서 덜 적합한 선수)를 나타낸다.

# 군집 오류 대상 찾기
df.loc[df['silhouette'] < 0]

실루엣 계수가 0보다 작은 데이터 포인트를 찾아 출력한다. 실루엣 계수가 0보다 낮은 경우 해당 데이터 포인트는 자신의 클러스터보다 다른 클러스터와 더 가깝다는 것을 의미하고, 이는 군집 오류 대상일 가능성이 크다.