이번 포스팅은 영상 입력에 관한 내용입니다.
이미지 이해
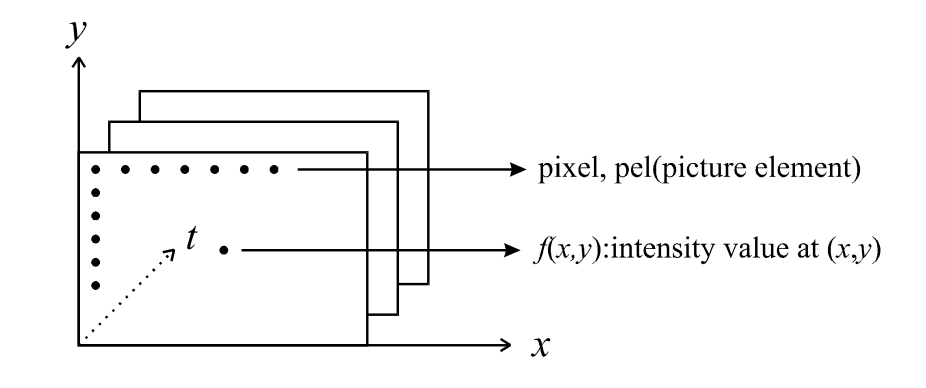
이미지(혹은 어떤 영상)는 우리 눈으로 봤을 때, 3차원의 형태로 보여지게 됩니다.
하지만 컴퓨터는 어떤 이산 신호(0 혹은 1값)로 나타나야 하기 때문에, 2차원의 형태로 받아주어야 합니다.
그래서
Sampling
이라는 것이 필요로한데,
어떤 자연계의 신호를 정수형태로 변환하는 과정이라 생각하면 됩니다.
결국에는 영상신호도 y = f(x)의 형태 (어떤 그래프의 형태) 로 나타낼 수 있다.
그리고 RGB전체는 각각 0~255까지의 값을 가지고 있고, 흑백 이미지는 8bit, color이미지는 24bit의 값을 가지고 있다.
이미지 픽셀 개념 접목
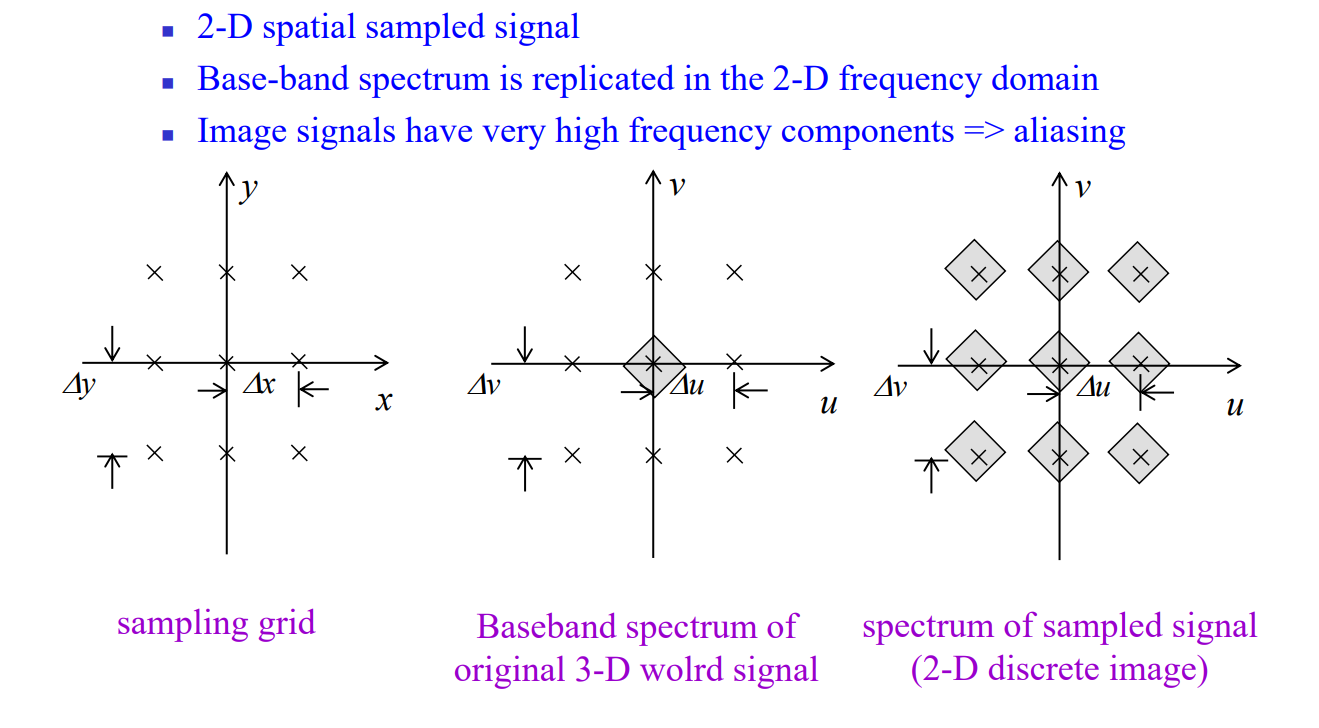
그림을 보면, 이미지 픽셀이 막 찍혀있는 것을 볼 수 있습니다.
이 픽셀의 간격을 sampling한다고 보면 되고,
이 간격이 촘촘할수록, 음원이나 영상 복원에 더 유용하다.
그림에는 쫌 어렵게 써져 있는데, 그냥 간단하게 이걸 Δx, Δy라고 표현했다고 보면 됩니다.
여기서 마름모 모양은 3차원 pixel을 뜻합니다.
그냥 그리기 편하게 저렇게 그렸는데, x,y,z 형태로 구성된 그림을 생각하면 참 좋다.
여기서 이 pixel(마름모)이 안겹쳐야 원래 이미지 형태를 더 잘 뽑아낼 수 있습니다.
하지만 영상에서 이게 안 겹치게 뽑아내는건 참 어렵다고 한다.
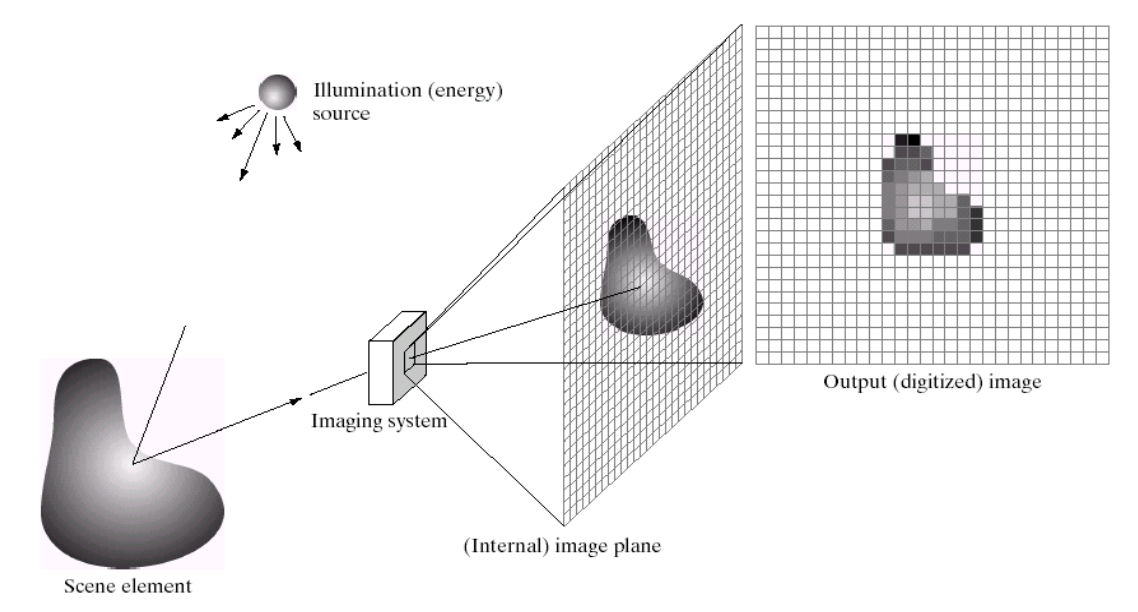
이런식으로, 어떤 광원이 있으면 물체를 비추게 되고, 이걸 렌즈를 거쳐다가 확대해보면, 어떤 그리드 형태의 픽셀 단위로 나타나게 됩니다.
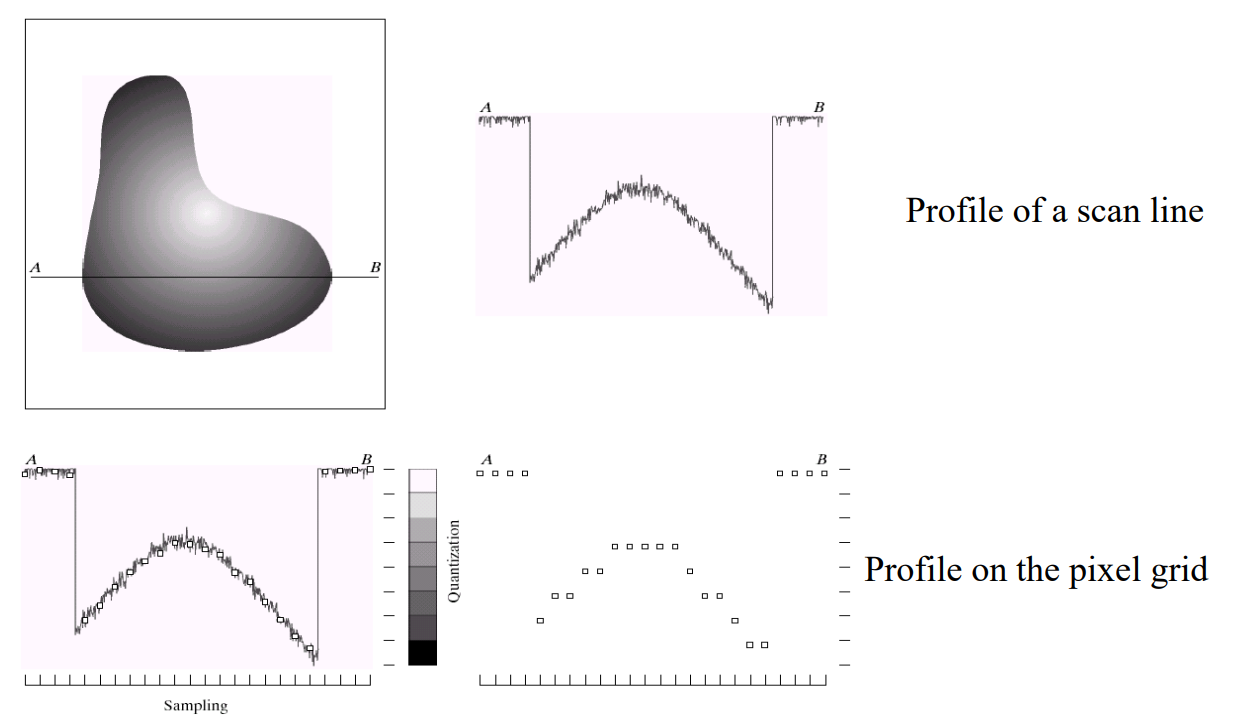
왼쪽 상단 A에서 B선으로 훑고 지나갈때, 이 값들을 나타낸게 오른쪽 상단 그래프 입니다.
오른쪽 상단 그래프와 왼쪽 상단 그림을 함께 보면, 흰색 파트일 때, 값이 높게 나오고, 검은색 파트에서는 값이 쫌 낮게 나오는 것을 볼 수 있습니다.
중간중간 지그재그 형태로 나타나는 것은 이미지에 noise가 껴있어서 이렇게 나오는 거라고 한다.
그리고 하단 오른쪽 그림은 왼쪽 그래프를 '양자화' 거치게 되면, 저런식으로 변한다고 한다.
Sampling? quantization(양자화)?
중간중간 샘플링, 양자화 라는 용어가 계속 나오는데,
Sampling: 어떤 continuous한 신호를 끊어서 측정하는 과정.
Quantization: Sampling된 값을 갖고, 실제 신호값과 가장 유사한 값을 뽑아내는 과정.
정의는 이렇게 나오나... 말이 참 어렵습니다....
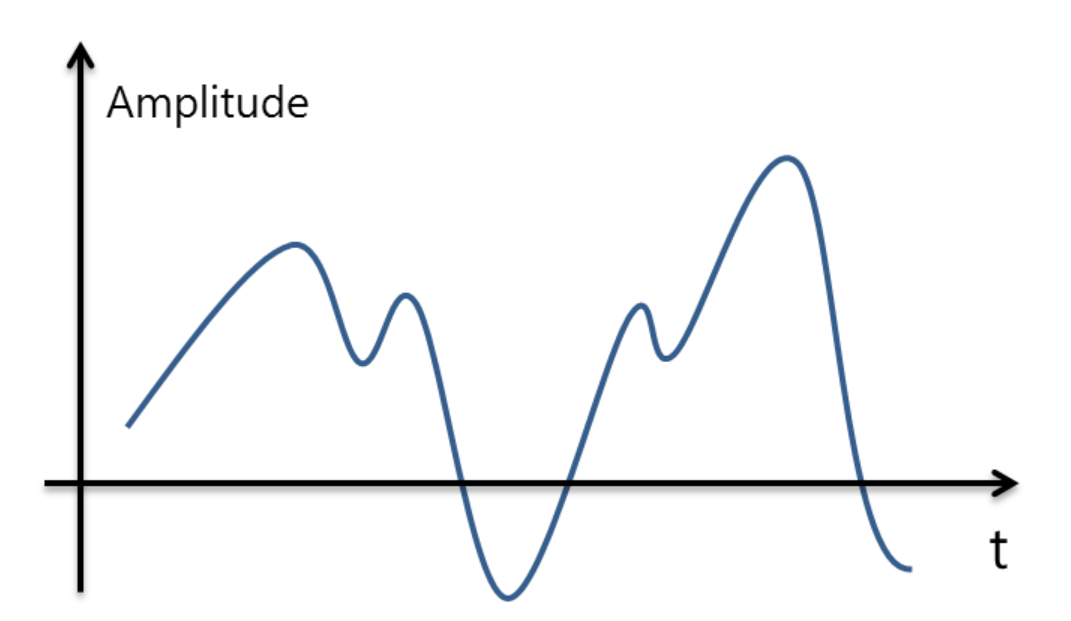
어떤 이미지의 실제 형태가 이런식으로 구성이 된다면,
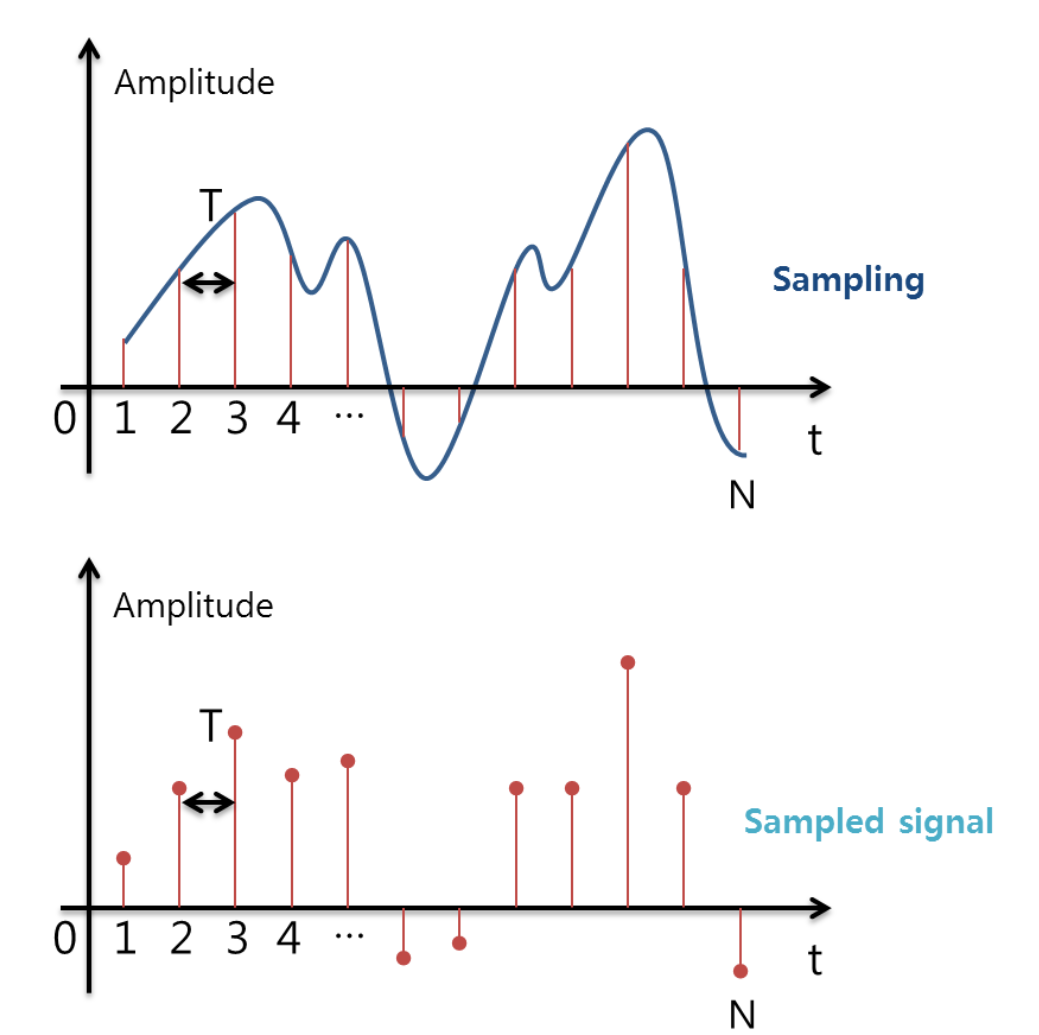
이렇게, 어떤 일정한 간격으로 뽑아내서 이걸 수치화 하는 것을 Sampling,
물론 이 간격이 최대한 촘촘해야 원래 신호와 더 유사.
그리고 이걸 어떤 의미있는 값들만 뽑아내는 것을 '양자화'라고 합니다.
자연계의 데이터는 무수한 값을 갖고 있기 때문에, 데이터를 어느정도 솎아내는 과정이 필요하다. 그래서 샘플링, 양자화 라는 것이 필요하고, 이게 독립된 관계가 아닌, 같이 연결된 관계로 보면 될 것 같다.

위의 그림은, 픽셀수가 높으면 샘플링 간격이 촘촘하다는 것이고, 해상도도 참 좋다는 것을 보여줍니다.
여담으로...

어떤 형태든 2차원 형태로 표현 가능하면, 다 image라고 합니다.
그리고 위의 이 3가지 이미지 덕분에 영상처리의 폭발적인 발전을 갖고 왔다고 합니다.
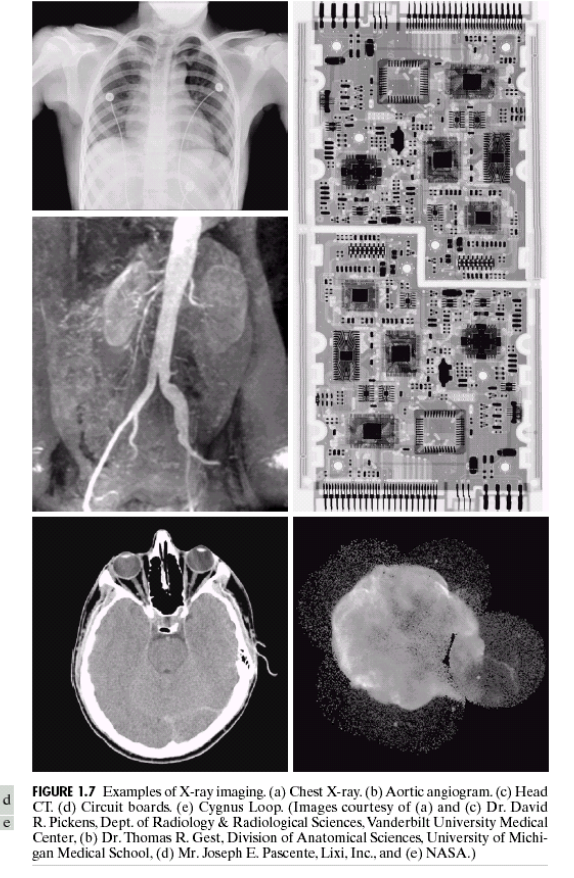
그리고 위의 이미지 같이, 뭔가를 투과해서 보여주는 이미지는, Noise값이 참 크게 나온다고 합니다.
Multi-spectral Images
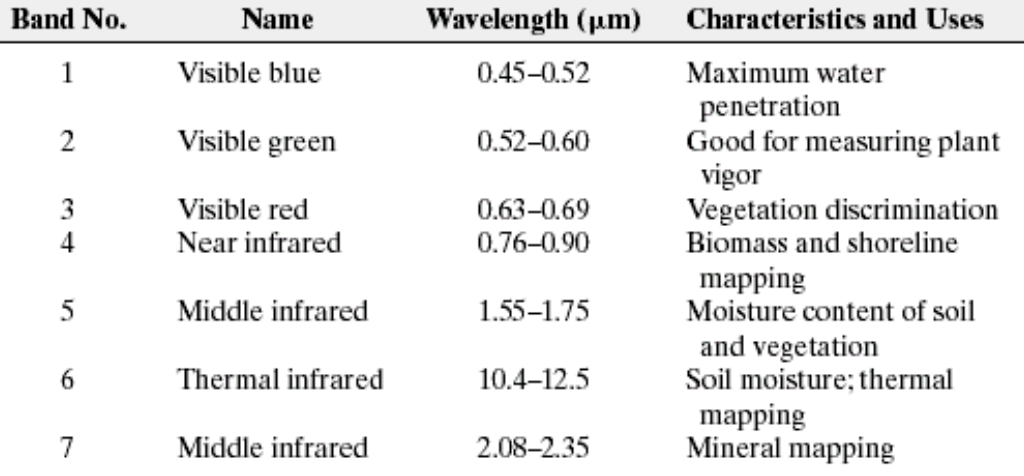
그리고, 색상별로 wavelength(파장)값이 달라지는 것을 알 수 있는데,
파장이 짧으면, 영상이 더 섬세하게 찍히고, 파장이 길면, 투과를 더 잘합니다.
위의 그림처럼, 초음파 사진을 예시로 들자면, 노이즈 값도 그만큼 크다.

위의 슬라이드는 이미지에서 많은 색상(RGB 정도의 색상이 아닌)을 찍으면, basis의 다양성이 더 풍부해져서 이미지를 더 정교하게 표현할 수 있다는 것을 말합니다.
하지만 이것도 결국 데이터의 양이 증가한다는 것이어서, 계산 비용이 늘어나게 됩니다.
Bayar CFA pattern
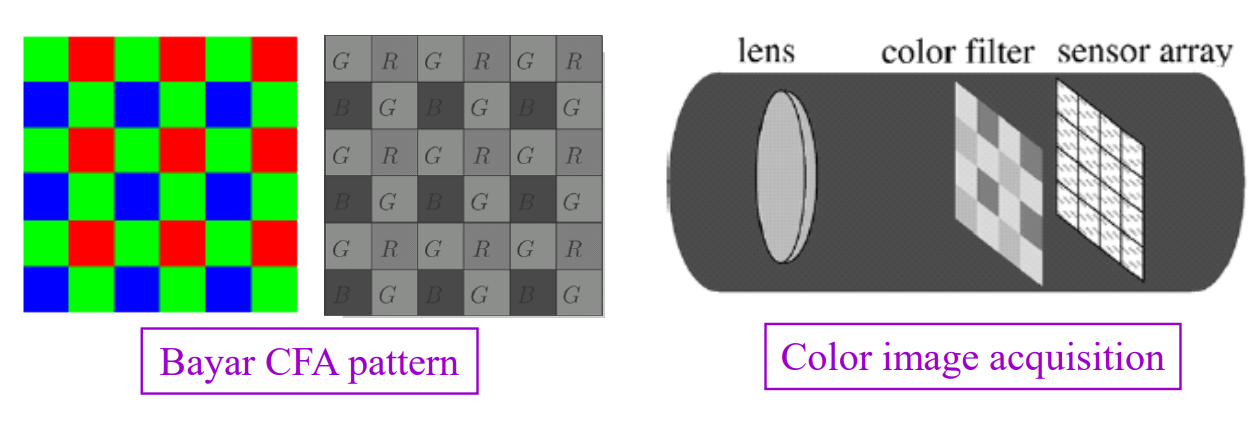
Bayer 패턴 입니다. 매우 오래전에 고안되었다고 하는데, 현재까지도 대부분의 카메라에 적용되어 있다고 합니다.
Bayer필터는 50%의 green, red 25%, blue 25%로 이루어져 있습니다.
사람의 눈은 초록색에 가장 민감하게 반응한다고 하는데, 그래서 Green의 비율이 압도적으로 높습니다.

위의 그림처럼, green색상이 더 섬세하게 나오는 것을 볼 수 있습니다.
Demosaic
Demosaic은 Bayer CFA 패턴으로부터 컬러 정보를 추출하는 과정입니다.

여기서 interpolation(보간)의 용어가 나오는데,
Horizontal Interpolation: 같은 '행'에 있는 인접한 픽셀 사이의 색상값을 추정하는 과정.
Vertical Interpolation: 같은 '열'에 있는 인접한 픽셀들 간의 색상값을 추정하는 과정.
Directional Interpolation: 주변 픽셀의 방향을 고려하여, 색상값을 추정하는 과정.
위의 그림은 이 보간법을 잘못 선택해서 위의 그림처럼 잘못 인식되게 되었고, 그나마 Directional Interpolation이 좀 정확하게 나온 것 같습니다.
어떤 이미지를 보고, 가로 방향의 선이 많은지, 세로 방향의 선이 많은지, 이걸 보고 보간법을 선택하면, 어느정도 잘 맞다고 합니다.
그냥 Directional Interpolation 쓰면 되는 거 아닌가? ㅎㅎ
감사합니당 ~ 🦾
