
이 포스팅은 An Introduction to Statistical Learning을 참고하여 작성하였습니다.
Linear Regression은 지도 학습의 한 범주입니다.
이 챕터에서는 선형 회귀를 집중적으로 다루었고, 차근차근 잘 살펴보도록 하겠습니다.
Linear Regression은 지도 학습의 한 범주입니다.
선형회귀로 풀 수 있는 문제는 총 7가지로 정리할 수 있는데,
- 광고 예산과 sales의 관계가 존재하는가?
- 또 얼마나 관련성을 갖고 있는가?
- sales와 어떤 미디어가 연관성을 갖고 있는가?
- 각각의 미디어와 sales는 또 얼마나 큰 연관성이 있는가?
- 미래의 sales 예측 정확도는 어떻게 할 수 있는가?
- 선형과 관련이 있는가?
- 광고 미디어와 시너지 효과가 있는가?
이것에 대한 답변을 하나하나 차근차근 살펴보도록 하겠습니다.
단순 선형 회귀는 굉장히 직설적으로 접근이 가능합니다.
수학적으로 나타내면,
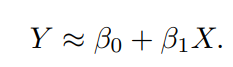
이렇게 되고,
X와 Y의 관계를 한눈에 파악 할 수 있습니다.
예를 들면 X에 TV를 넣고,Y에 sales값을 넣으면, B_0, B_1값(계수 혹은 파라미터)값을 얼추 알 수 있습니다.
그리고 y^을 어떤 추정값, y값을 실제값이라고 하면, 이 둘 사이의 차이를 error로 볼 수 있습니다.
이 error계산 중에 하나가 RSS(residual sum of squares)라는 것이 있는데,
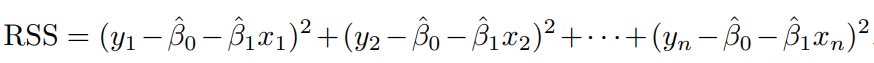
식이 이런식으로 구성이 됩니다.
이 RSS값을 최소화 하는것이 우리의 숙제라고 볼 수 있습니다.
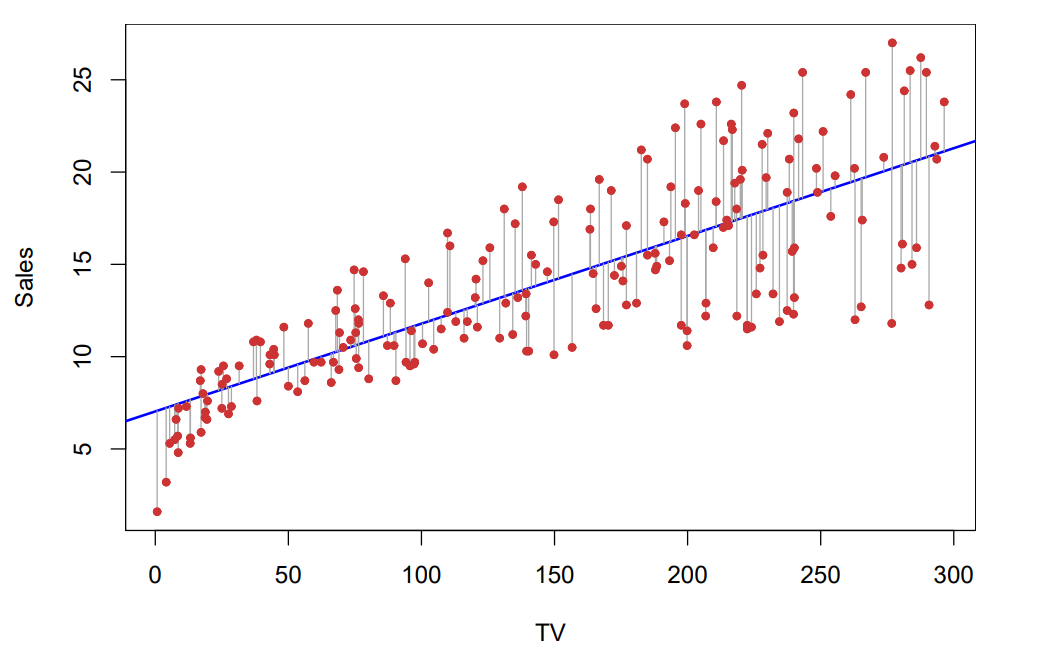
이 그래프를 보면, 선형회귀와 각각의 데이터 사이의 거리를 잘 파악할 수 있습니다.
검은 선이 오차를 의미합니다.
그리고
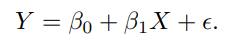
위 식이 나옵니다.
아까 보았던 식에서 무언가 더 추가된 기분입니다.
여기서 E는 오차항이고, B_1을 기울기로 보면 됩니다. 그리고 B_0는 절편값.
그냥 일차 함수 생각하면 편하다.
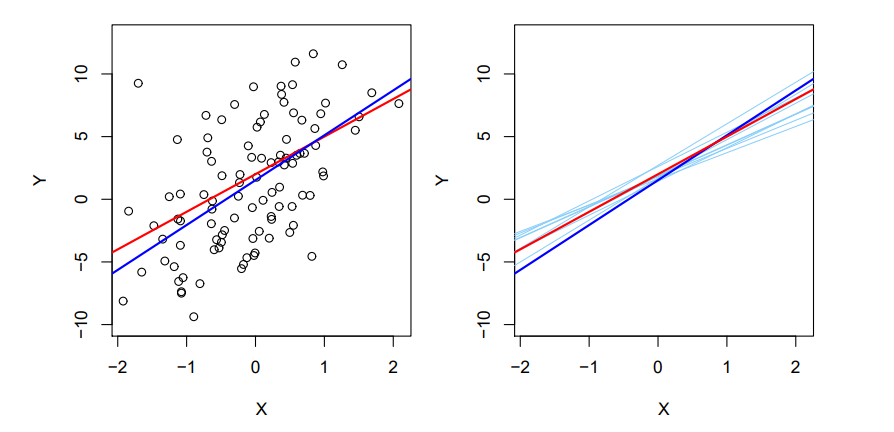
Regression line과 Least Squares Line의 개념이 나옵니다.
회귀선은 Data를 잘 설명하는 선형, 비선형의 어떤 선이라고 하면,
Least Squares Line은 회귀선과 실제 Data들 간의 수직거리를 최소화 하는 방법으로 볼 수 있습니다.
위 두 그림이 잘 설명 해주는데, 빨간 선이 실제 관계를 뜻하고, 파란선은 Least Squares Line을 뜻합니다.
얼추 일치하는 것이 보이는데, 이는 데이터가 참 많기 때문에 그렇습니다.
그리고 SE(Standard Error)라는 것도 나옵니다.
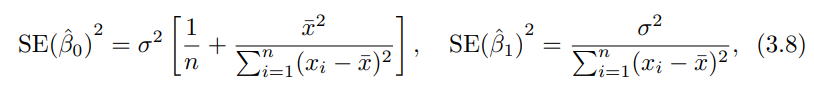
수식은 이렇게 정의되고, 이 SE로 신뢰구간을 다룰 수 있습니다.
선형회귀에서는 신뢰구간을
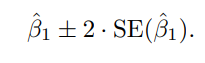
라고 하는데,
만약 신뢰구간을 계산하면, 평균 6130 ~ 7935의 판매량일 때, 1000달러 증가할 때마다 평균 42 ~ 53의 판매 증가가 있음을 계산을 통해 알 수 있습니다.
이런게 수식으로 정리되어 있는줄은 몰랐다.
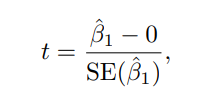
이 식은 t-statistic 입니다.
이것으로 각 변수의 연관성을 알 수 있는데, 이 값이 작으면 X와 Y는 아무 관계가 없다는 것이고, 또 이 값이 크면 서로 강한 연관을 갖고 있다고 합니다.
P-value도 있습니다. 이는 t-statistic이 어떤 주어진 값 이상일 확률을 말하는데,
p-value가 작을 수록, x,y 사이의 관계가 올라가기 때문입니다.

이 표 예시를 보면, t-statistic이 높고, p-value가 낮아서 광고예산과 판매량 사이의 연관성이 높습니다.
그리고 Linear Regression의 평가법이 나왔습니다.
1. RSE(Residual standard error)
2. R^2
총 이렇게 두가지가 나왔습니다.
간략하게 설명하자면,
RSE는 말그대로 실제 데이터에서 회귀선이 얼마나 벗어났는지 알 수 있게끔 계산하는 것을 말합니다.
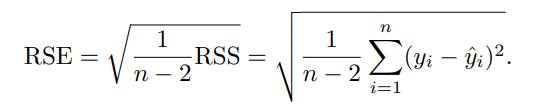
만약 RSE를 계산했는데, 이 값이 매우 크다면 모델이 Data에 잘 맞지 않다는 것을 의미합니다.
R^2는 RSE의 항상 잘 들어맞지 않는 단점을 보완했는데, 항상 0~1 사이의 값을 갖고, 서로 독립적인 특징을 갖고 있습니다.
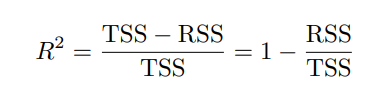
이 식에서 처음 보는 TSS가 나오는데, 이는 분산 측정하는 식이고,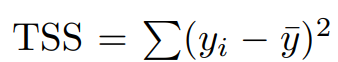
의 식을 갖고 있습니다.
그냥 똑같이 제곱의 합이다.
TSS는 회귀 전에 변화의 양을 측정하는 것이고,
RSS는 회귀 후에 변화의 양을 측정하는 것입니다.
양은 그냥 sum으로 보겠다.
그래서 TSS - RSS는 Regression 수행 전, 후에 변화가 얼마나 제거되었는지 보여줍니다.
또한 R^2이 1에 가까우면 Regression으로 설명 가능하고, 0에 가까우면 Regression반응 설명 불가능 하다는 특징을 갖고 있습니다.
그래도 RSE보다는 해석에 좋다고 합니다.(0~1사이의 값을 가져서)
그리고 또 좋은 점은 R^2으로 상관관계도 측정이 가능합니다.
TSS를 약간 변형한 형태이다.
하지만 한가지 단점이 있다면, 다중 선형 회귀(Multiple Linear Regression)에서는 예측할 변수가 많아서 R^2이 먹히지 않는다고 합니다.
다중 선형 회귀는 여러개의 예측변수를 가지게 됩니다.
다중 선형 회귀를 위해 한가지 잘못된 접근 방식을 말했는데,
'단순 선형회귀'를 따로 따로 실행하는 방식을 쓰면 안되나? 라는 말을 했습니다.
하지만,
1. 단일 예측을 어떻게 해야하는지에 대한 의문.
2. Regression 방정식은 하나만 고려가능.
이 두가지 이유 때문에 다른 방식으로 접근해야 한다고 했습니다.
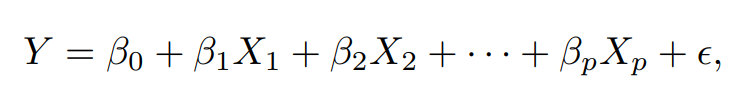
그래서 다중선형회귀에서는 이 식을 갖다 씁니다.
X_1, X_2, X_3, ... , X_p에는 여러 변수 적용.
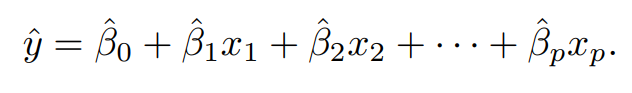
어떤 계수값에 대해서 이런식으로 계속 계산을 하면 최종 y^값이 나오게 됩니다.
하지만 이것도 결국에는 예측한 값이기 때문에, 실제 값과의 차이가 나올 수 밖에 없습니다.
그래서 얼마나 차이가 나는지 확인이 가능한데, 그 식이
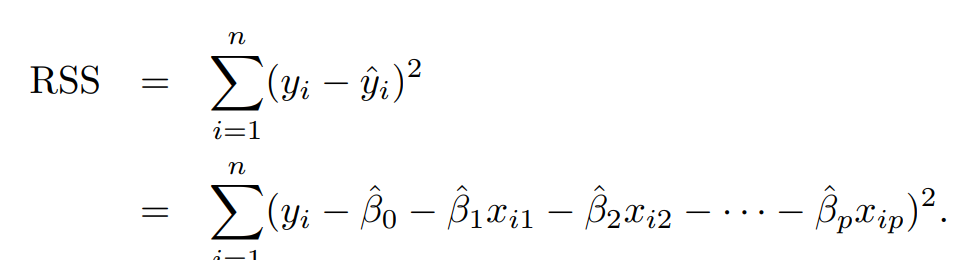
이렇게 구성되어 있는 RSS입니다.
위에서도 나왔으나, 다중선형 회귀이기 때문에, 모든 오차값을 sum하는 형태로 나오게 됩니다.
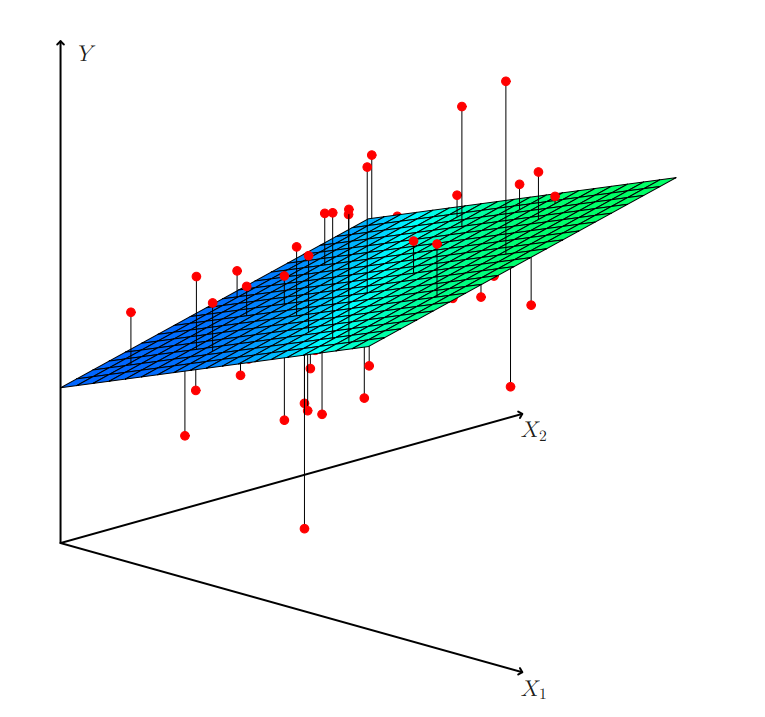
이런식으로, 단순선형 회귀는 2차원 형태의 직선 모양이 나왔다면, 다중선형회귀는 3차원 형태의, 어떤 판 모양으로 예측하게 됩니다.
다중선형 회귀에 대한 의문을 정리하자면,
1. 응답과 예측 사이에 관계가 있는가?
2. 모든 predictors가 Y를 설명 가능한가, 아니면 일부만 가능한가?
3. 모델이 Data에 얼마나 잘 맞는가?
4. 예측 변수에 대해 어떤 응답변수 값을 예측해야 하는지, 또 정확도는 얼마인지?
로 정리할 수 있습니다.
차근차근 하나하나 살펴보도록 하겠습니다.
1. 응답과 예측 사이에 관계가 있는가?
단순 선형 회귀에서는 B_1이 0인것만 확인하면 됐습니다.
하지만 다중선형 회귀에서는 B_1 = B_2 = ... = B_p = 0 인 것을 확인해야 합니다.
이걸 여기서는 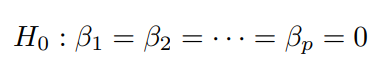
로 설명을 했습니다.
그리고 적어도 하나의 B_j가 0이 아닌지 확인 해야 하는데, 이건 F-statistic. 즉
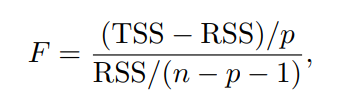
이 식을 통해서 확인하면 되고, 이 값이 1에 가깝다면 Response랑 predictors가 서로 관계가 없음을 의미합니다.
그리고 H_a, 즉,

이 정의가 참이면, F-Statistic값이 1보다 큰 값을 가지게 됩니다.
2. 모든 predictors가 Y를 설명 가능한가 아니면 일부만 가능한가?
이건
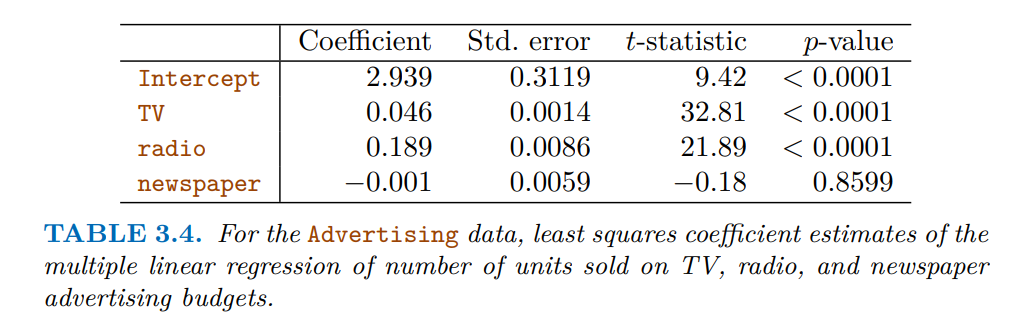
이 테이블을 예시로 들었는데, t-statistics, p-value값이 나옵니다.
이것이 predict와 response와의 관계를 나타내는데, 이걸로 모든 predictors가 Response와 연관되어 있는지 선뜻 판단하면 안된다고 합니다.
3. 모델이 Data에 얼마나 잘 맞는가?
Model fit은 F-statistics로 알 수 있습니다.
H_a가 참이고, 오차가 normal distribution 형태라면, F-statistics는 F-distribution을 따릅니다.
4. Predictor values에 대해 어떤 reponse value값을 예측해야 하는지, 또 정확도는 얼마인지?
다중선형 회귀 파라미터를 추정해서 하면 됩니다.
이 추정된 파라미터로 Predict하고, 이 정확도는 RSS를 통해 알 수 있습니다.
대부분의 Response는 Predictors의 일부분만 연관이 있습니다.
그래서 서로 연관이 있는 변수를 뽑아내는 경우가 종종 있는데, 이것을
'Variable Selection'
이라고 합니다.
여기서 p개의 변수를 넣는 모델 개수는 2^p개의 모델을 갖는다고 합니다.
왜 모델 개수가 이렇게 구성되는지는 끝내 이해하지 못했다.
이와 같이, 이렇게 직접 뽑아서 넣는 것은 현실적으로 불가능하기 때문에,
1. Forward Selection
2. Backward Selection
3. Mixed Selection
와 같은 방식을 사용하게 됩니다.
Backward selection은 변수의 수가 Data의 양보다 많으면 사용 불가능하고,
Forward selection은 항상 가능한데, 필요없는 변수도 같이 껴들어 갈 수 있어서 별로 좋지 않은 방식이라고 합니다.
그래서 이 두가지를 섞어서 쓰는 방식이 있는데, 이를 Mixed Selection이라고 합니다.
모델 적합성 측정 방식에는 RSE, R^2이 있습니다.
각각의 설명은 위에서도 했기 때문에 넘어가고,
R^2값이 1에 가까울 수록, 분산과 큰 연관이 있습니다.
이 책에서 예시를 들어줬는데, TV, Radio, 신문광고의 값이 0.8972,
여기서 신문 광고를 뺀게 0.89719로 구성이 되면,
여기서 신문광고의 p-value는 중요하지 않음을 의미합니다.
그리고 특정 변수를 넣고, 빼고 하다가 R^2값이 올라간다 하면, 그 변수는 좋은 변수라고 합니다.
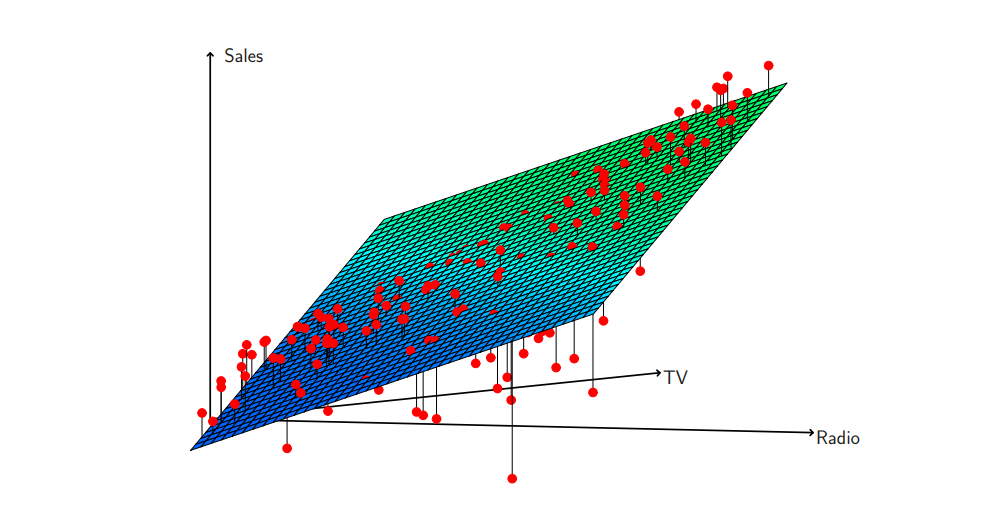
이 그림에서는, Regression 판 위, 아래에 데이터가 분포하고 있는 것이 보입니다.
이는 변수 한개보다, 여러개의 변수가 판매율에 더 많은 도움이 됨을 암시합니다.
그리고 fit한 다음에, predict할 때에 대한 이야기가 나왔습니다.
정리하자면...
- Coefficient 추정치는 실제 값에 대한 추정에 지나지 않는다.
이 차이는 Confidence interval(신뢰구간) 계산을 통해 측정 가능하고,- Linear model은 실제 데이터에 근사값에 지나지 않는다. 이에 대한 오차를 '모델 편향'이라 하고.
- B_p(계수)값을 정확히 알고 있다고 해도, 완벽한 예측은 당연히 불가능하다.
이는 Prediction intervals로 측정 가능하다.
로 정리할 수 있습니다.
여기서 계속 나오는 '신뢰구간'은 불확실성을 좀 정리하는데 사용된다고 합니다.
개별 Data들이 Regression 판때기와 얼마나 다를지에 대한 불확실성을 포함하기 때문에, 예측 구간은 신뢰 구간보다 항상 Wider한 형태를 띄게 됩니다.
Quantitative(양적): 나이, 카드 수, 소득, 신용 등급
Qualitative(질적): 학생상태, 결혼상태, 지역
양적은 뭔가 어떤 특정 값으로 단번에 나타낼 수 있는 것, 질적은 값으로 나타내기 애매한거로 생각하자.
전처리 할 때 Qualitative는 그래프 그리거나, 학습시킬 때, 바로 안들어가는데, 이를 수치화 하는 것을 '더미 변수'라고 합니다. (0,1값으로 바꾸는 것)
더미 변수로 만들어 버릴 때, 주의할 점이 있는데, 이렇게 하면 p-value가 매우 높다고 합니다.
당연한게, 임의로 값을 바꿔버린 것이기 때문에, 변수들 사이에 뭔가 명확히 표현할 것이 없어서 그렇습니다.
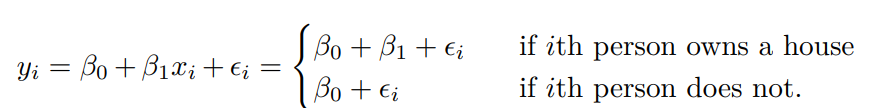
굳이 식으로 나타내면 이렇다고 합니다.
꼭 0,1 값으로만 바꿔야 하는것은 아니다. 본인한테 맞춰서 값 바꿔줘도 된다.
위에서는 두가지 레벨의 경우만 다뤘습니다.
보통 3개 4개의 레벨을 넘어가는 경우가 참 많은데,
이때는 더미변수를 여러개 생성해주면 그만입니다.
이것도 굳이 식으로 나타내면,
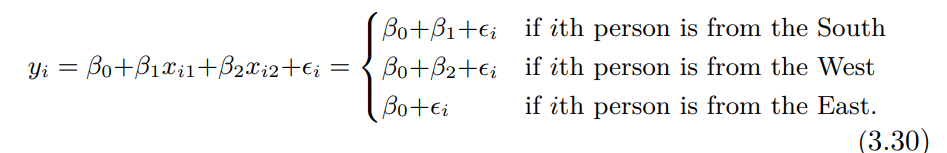
이렇게 되고,
범주형(질적), 수량형(양적) 둘다 있다면, 범주형을 더미로 돌리고, 두개 다 같이 Regression 변수로 사용하면 됩니다.
Linear 모델 개념을 확장한 것이 나왔습니다.
위에서 살펴보았던 Linear Regression은 다른 변수들과 어떤 상호작용이 안보였는데,
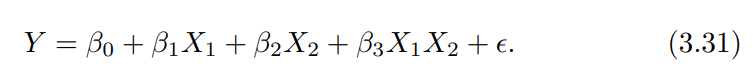
이 식처럼 중간에 X_1, X_2를 곱한 것이 보입니다.
이걸 Interaction term(상호작용 항)이라고 하고,
예시에 적용하면,

이렇게 됩니다.
TV, Radio를 중간중간 막 껴 넣어서 두 변수가 서로 얼마나 영향을 끼치는지 알 수 있게 됩니다.
이 Interaction term을 확실히 알려면, p-value계산을 하면 된다. 이 p-value값이 너무 낮으면, 변수들 사이의 상호작용이 크다는 것을 의미한다.
Polynomial Regression
앞에 매우 장황하게 설명을 했는데, 요약하자면,

자연계 데이터는 대부분 Non Linear일 가능성이 높아서, 다항식 회귀를 사용하게 된다라고 합니다.
그리고 선형 회귀 모델을 데이터에 적용할 때 문제 몇가지를 제시 했는데,
1. Non-linearity of the response-predictor relationships
2. Correlation of error terms
3. Non-constant variance of error terms
4. Outliers(이상치)
5. High-leverage points
6. Collinearity
입니다.
1. Non-linearity of the response-predictor relationships
Linear로 예측을 했는데, 실제 Data가 그렇지 않을 가능성이 매우 큽니다.
비선형적임을 말하는 것이다.
이렇게 되면 정확도도 매우 낮아지게 됩니다.
그래서 나온게,
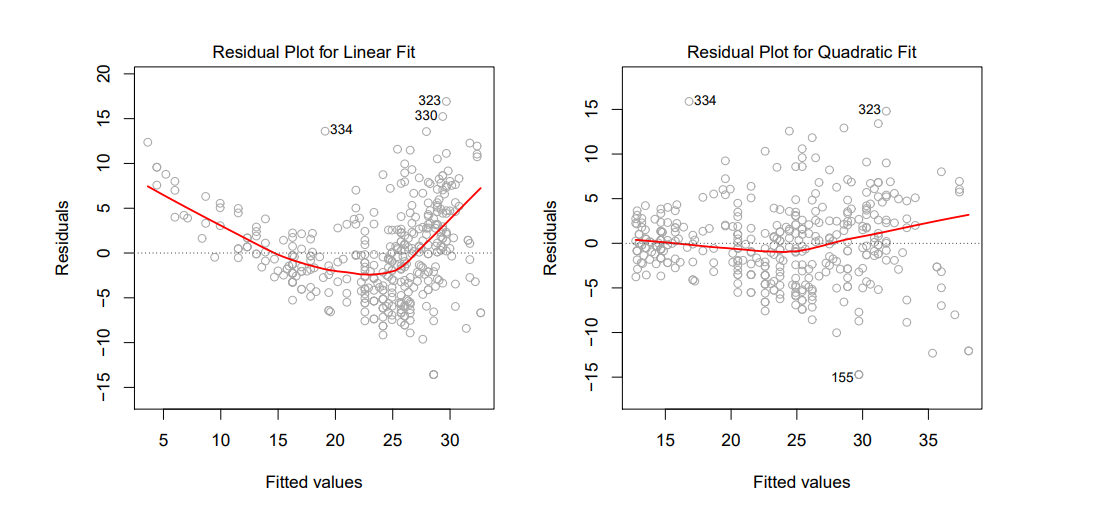
Residual Plot입니다.
여기서는 대충 이렇게만 언급하고 넘어갔다. 뒷부분에서 자세히 다룬다고 하니, 일단 어떤 오차값이라고 생각하고 넘어가자.
2. Correlation of error terms
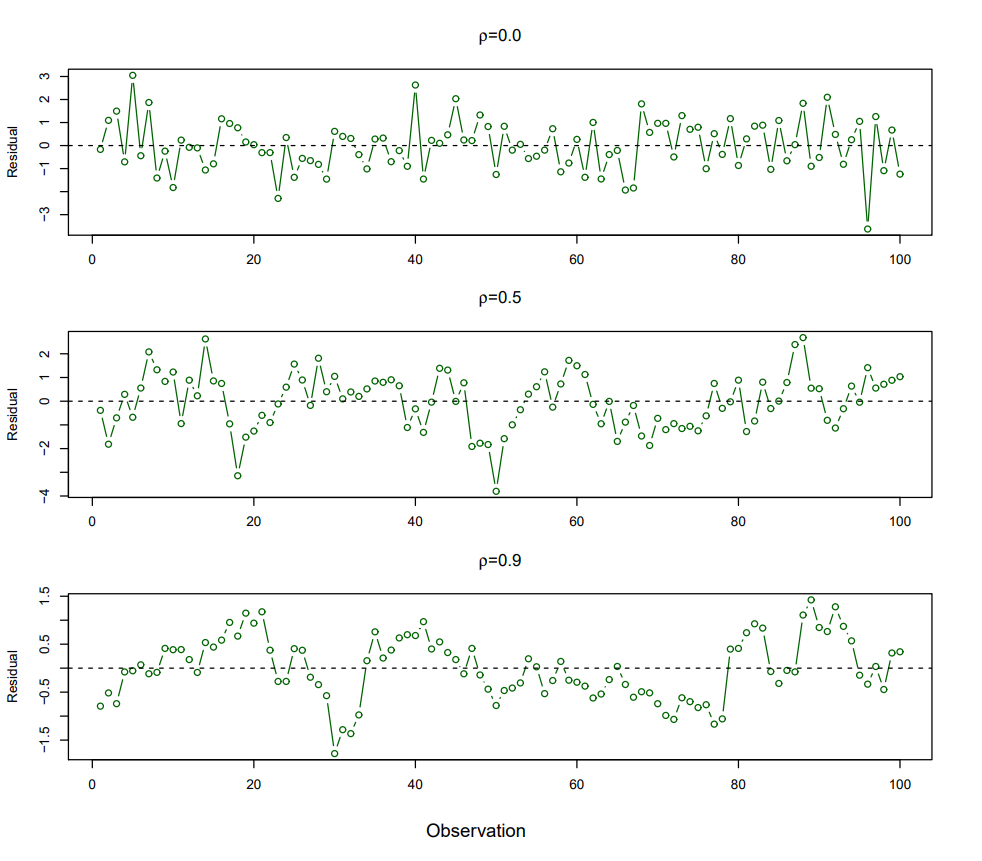
Linear Regression 모델에는 correlation이 없습니다.
만약 error term(오차항)에 상관관계가 있으면, Underfitting 문제가 발생합니다.
오차항 correlation은 시계열 Data에서 주로 발생하는데, 위 그림에서 처럼, 오차항에 correlation이 있으면, 특정 패턴이 보이게 됩니다.
3. Non-constant variance of error terms
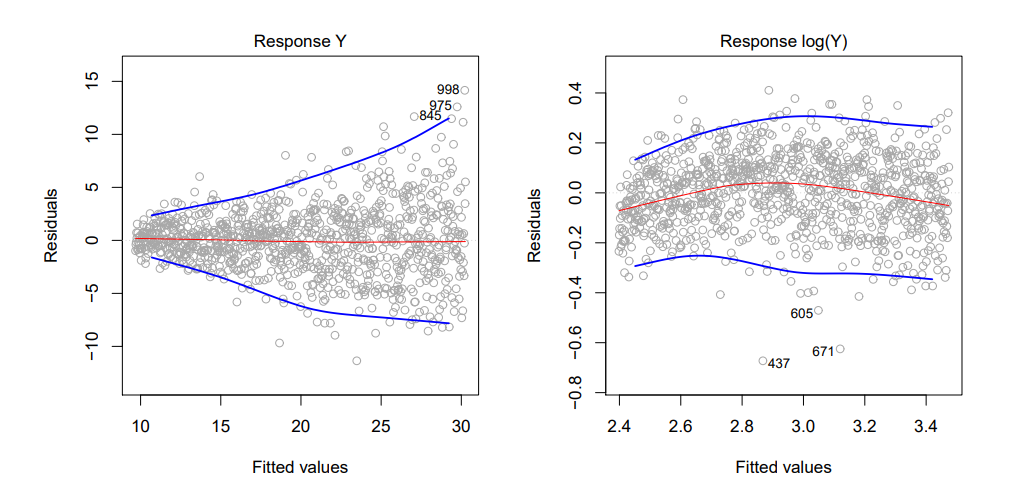
그리고 Linear Regression 모델은 일정한 분산을 가지는데,
여기서 오차항 분산이 일정하지 않으면, 바로 위 그림처럼 세모? 마름모? 모양이 나오게 됩니다.
이 해결책으로 log를 씌우거나, 루트를 씌워 변환하는 방법이 있다고 합니다.
또한, 분산값을 알고 있으면, Weighted Least Squares를 써서, 모델을 fit하게 만들 수 있다고 합니다.
4. Outliers(이상치)
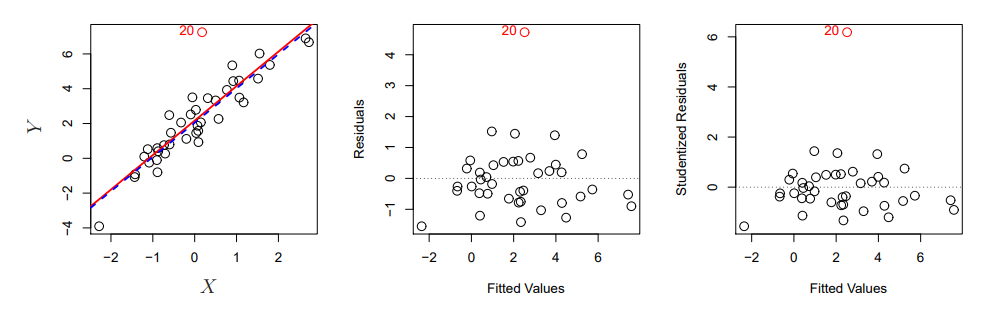
이상치라는 것은 모델이 예측값에서 크게 벗어난 것을 의미합니다.
데이터 수집 과정에서 정신 안 차리고 하면 발생하는 문제입니다.
이건 이제 Least Squares Regression에서는 잘 안 나타나는데,
RSE, R^2에서는 큰 영향을 줍니다.
그래서 위와 같이 Residual Plot을 찍어봐야 합니다.
해결책으로 단순 drop을 말했는데, 이것도 잘 보고 해야한다고 합니다.
데이터 좀 처음부터 잘 주면 참 좋겠다.
5. High-leverage points
leverage 높다는 것은 x_i값이 다른 관측에 비해 쫌 이상한 값을 가질 때 발생하는 문제입니다.
Least Squares에 큰 영향을 끼치므로 잘 판별하도록 해야합니다.
판별할 때,
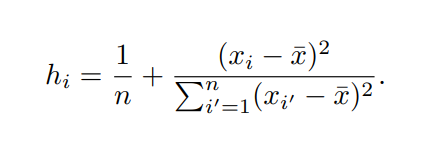
위의 leverage statistic 이라고 불리는 계산을 해봐야 하는데, 이 값이 크게 나오면, leverage가 높다는 것을 의미합니다.
처음에 leverage? leverage가 뭐지? 했는데, 한글로 영향력이라고 한다. 제곱 합, 제곱 합은 계속 반복된다.
6. Collinearity
Collinearity는 여러개의 변수가 밀접하게 연관되어 있는 것을 의미합니다.
그래서 변수 하나가 증가하거나 감소하면, 다른 하나도 똑같이 변하게 되는데,
이런 현상 때문에, 각 변수가 반응변수에 얼마나, 어떻게 연관되어 있는지 잘 모르게 됩니다.
Collinearity는 계수 추정치의 정확도를 내려가게 해서, B^_j의 오차를 증가시킵니다.
그래서 t-statistic을 감소시키고, H0 : βj = 0 이런 무시무시한 현상을 보게 되는데,
이건 0 아닌 계수를 알아 맞히는 power가 감소한다는 것을 의미합니다.
이걸 탐지하는 방법으로 Correlation Matrix를 찍어보는 것이 존재한다고 합니다.
세개 이상의 변수 사이의 collinearity(Multicollinearity) 존재할 수 있어서 무조건적으로 이걸 쓴다고 되는 것은 또 아니라고 합니다.
이걸 평가하는 좋은 방법은 VIF 계산하는 것인데,
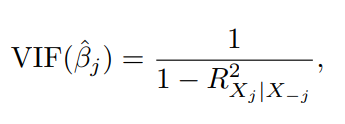
식은 이렇게 구성됩니다.
VIF 값이 1이라면, Collinearity가 전혀 없는 것이고, 5 ~ 10을 초과하면, 문제가 있는 것입니다.
collinearity 해결책을 정리하자면,
1. 문제 되는 변수 하나 제거.
2. Collinearity 변수를 예측변수 하나로 결합하는 것(ex. limit & rating 변수의 평균을 새로운 변수로)
이렇게 됩니다.
감사합니당 ~ 🦾
