Linear Regression part 2

이 포스팅은 An Introduction to Statistical Learning을 참고하여 작성하였습니다.

---

앞쪽 부분은 Linear Regression part 1에 대한 정리입니다.

1. 매출과 광고 예산 사이에 관계가 있는가?

Multiple Regression Model로 relationship 판단 가능합니다.

이는 구체적으로 'F-statistics'로 광고 매체가 매출에 어떤 영향을 주는지 판단 가능합니다.

2. 관계 강도는 얼마나 큰가?

이는 두 가지, 즉 RSE와 R^2으로 추정 가능한데,

RSE로 Response의 표준편차를 측정하고,

R^2로 Predictors가 Response의 변동성을 얼마나 갖고 있는지, 확인 가능합니다.

3. 어떤 media가 매출에 관계가 있는가?

이는 t-statistics의 p-value를 확인해서 판단 가능하다고 합니다.

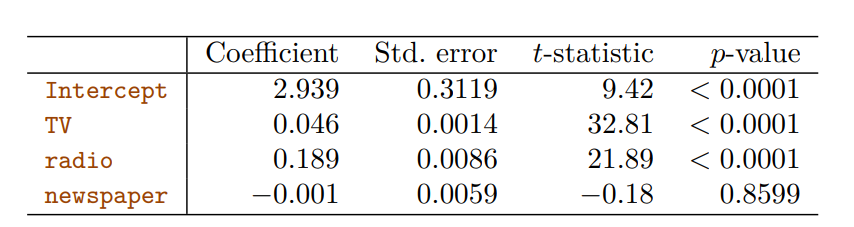
위 표를 보면, 'TV와 Radio'는 Sales에 큰 연관을 갖고 있음을 알 수 있습니다.

p-value값이 낮음

하지만 Newspaper는 아닌 것을 확인할 수 있습니다.

4. media 와 매출 사이의 관계는 얼마나 큰가?

B^_j의 오차를 통해서 B_j의 confidence intervals(신뢰구간)을 알 수 있습니다.

위의 표를 보면, Newspaper의 Confiddence를 보면, 0이 껴있는 것이 보입니다.

그래서 이는 통계적으로 관계가 없음을 뜻합니다.

5. 미래의 매출을 얼마나 정확하게 예측 가능한지?

Prediction interval(예측 구간) 이나 Confidence interval(신뢰구간)을 써서 Response 예측 가능합니다.

보통 Prediction interval이 Confidence intervel보다 클 수 밖에 없다.

6. 선형 관계인가?

Residual plot(잔차 plot)으로 Non-linearity 판단 가능하고,

7. 광고 Media 사이에 시너지 효과가 있는가?

Linear Regression에는 Predictors와 Response 사이에 addictive Relationship(덧셈관계)가 존재한다고 합니다.

이게 모든 Data set에 다 들어맞지는 않고,

Interaction term(상호작용 항)을 포함하면, R^2이 크게 증가합니다.

---

이번에는 KNN에 관한 이야기 입니다.

Linear Regression은 매우 간단하게 predict하는 것이 가능합니다.

하지만 실제 측정값이 멀리 떨어져있다면, 이는 정확도를 낮추는 큰 요인이 됩니다.

Linear Regression을 parameteric 이라는 용어로 설명했다.

Non-parameteric 방법 중 하나인 KNN Regression은 Linear Regression보다 더 유연한 특징을 가지고,

여기서 K 값은 bias-variance trade off(편향 - 분산 트레이드 오프)에 따라 달라집니다.

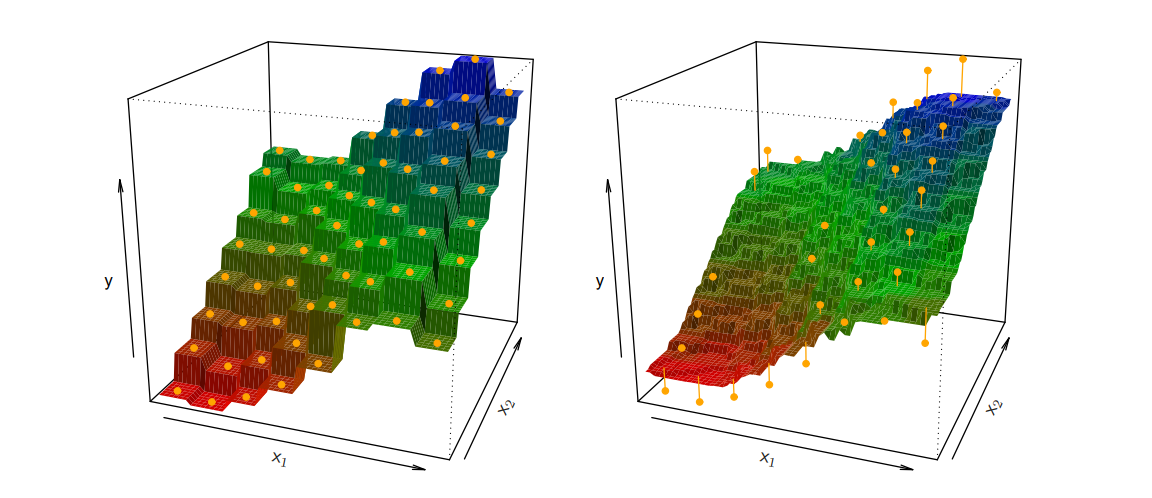
위의 왼쪽 그림은 K가 1일 때의 그림이고, 오른쪽 그림은 K가 9일때의 그림입니다.

딱 봐도 K가 크면 클 수록, 예측을 훨씬 부드럽게 하는 것이 보입니다.

하지만, 무조건 K가 크면 클 수록 좋은 건 아닌게, bias(편향)값이 커지는 것도 고려를 해야합니다.

예를 들면, Data가 일차원 형태여서 이걸 Linear Regression으로 접근하는 것이 이상적입니다.

여기서 이걸 KNN Regression으로 접근을 한다면, bias값 낮고, variance값은 높게 나오게 됩니다.

---

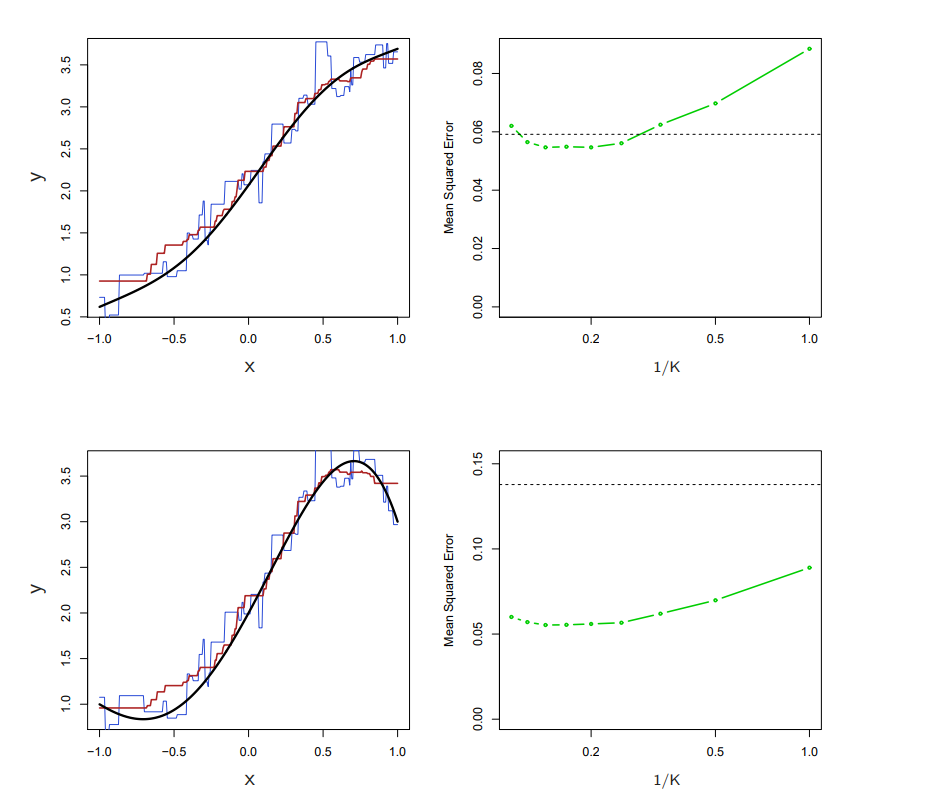
위의 그래프는 K값에 따른 MSE의 변화를 보여줍니다.

Blue가 1, Red가 9, MSE의 검은 점선이 Linear Regression MSE 점수.

첫번째 행을 보면, K값이 낮으니 Linear Regression의 MSE가 KNN보다 더 좋습니다.

하지만 k가 4를 넘어가는 순간, KNN이 Linear Regression보다 MSE 값이 더 높아지는 것이 보입니다.

그 아래 행은 모든 KNN이 Linear Regression보다 성능이 더 좋은 것으로 보이는데,

이것이 암시하는 것은, 다음과 같습니다.

Data의 형태가 복잡하면 복잡할 수록, KNN Regression이 더 적합하다.

---

그런데, 또 이게 막 맞는 건 아닌게,

보통 선형 관계일때는, Linear Regression이 좋고,

비선형 관계일때는, KNN이 더 좋다고 생각이 드는데,

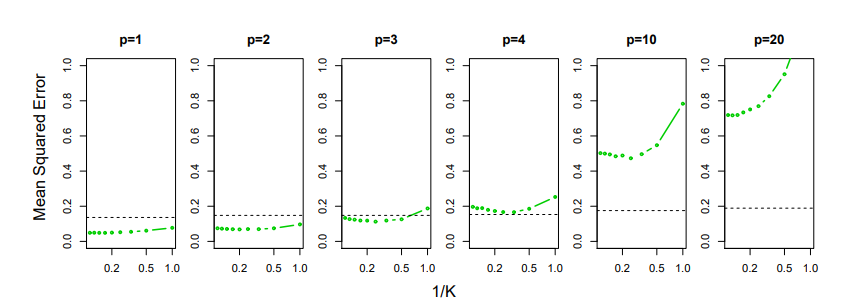
또 차원이 높으면 높을 수록, KNN이 Linear보다 더 좋지 않다고 합니다.

위의 그림을 보면, p값이 높아질 수록, MSE값은 폭발적으로 올라간다.

이게 차원이 증가하면, 표본 크기가 줄어드는 문제가 생겨서 그런건데,

이런 문제를 우리는 'Curse of Dimension(차원의 저주)' 라고 부릅니다.

맨 마지막에 차원이 작다고 Linear가 더 좋을수도... 안 좋을수도... 그러는데, 항상 이쪽 분야 종사자한테 자문을 구하면, 항상 애매하게 이런식으로 답변한다.

어찌보면 당연한게, 적용해보기 전까지는, 정말 모르기 때문이다.

암튼 그렇다.

---

감사합니당 ~ 🦾