소개
- 이 글은 단지 CS231n를 공부하고 정리하기 위한 글입니다.
- Machine Learning과 Deep Learning에 대한 지식이 없는 초보입니다.
- 내용에 오류가 있는 부분이 있다면 조언 및 지적 언제든 환영입니다!
참조
-
https://jeongukjae.github.io/posts/CS231n-Lecture-5.-Convolutional-Neural-Networks/
-
https://younghk.netlify.app/posts/cs231n-lec5-convolutional-nerual-networks/
-
https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1
-
https://medium.com/@pavisj/convolutions-and-backpropagations-46026a8f5d2c
개요
< Convolutional Neural Networks >
Reminder Previous Lecture
시작하기 앞서서 전에 배웠던 Neural Networks(NN) 의 모습입니다.
아래 사진을 보고 기억나지 않는 것이 있다면 전 강의를 다시 돌아가서 봐주세요!
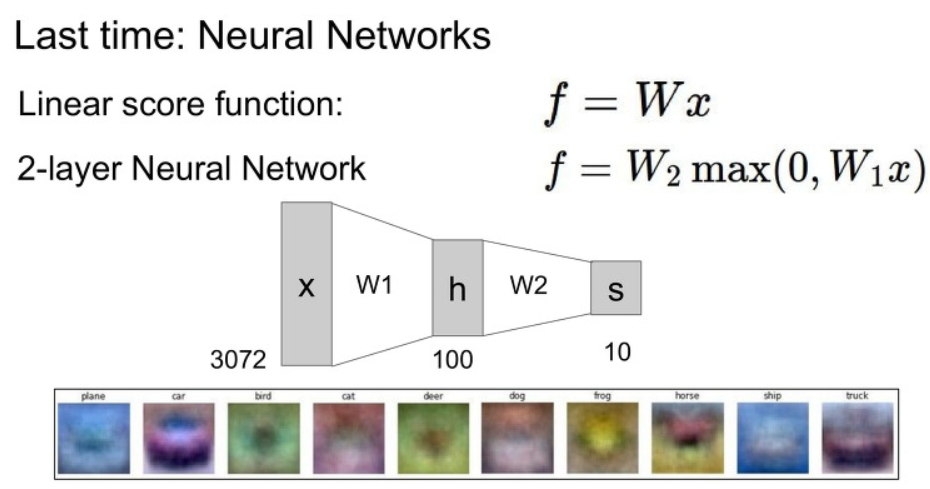
Fully Connected Layer
CNN에 대한 설명을 시작하기 전에 전에 시간에 배운 Fully Connected Layer에 대해서 집고 넘어가봅시다.
Fully Connected Layer에서는 이미지를 1차원으로 펴서 weight 값과 곱해주는 것을 볼 수 있었습니다.
또한 여기서 필요한 weight의 갯수는 input image x class number인 점을 살펴봅시다.
첫번째 image를 1차원으로 펴서 사용한다는 점에서 image에 지역적 정보를 사용할 수 없다는 단점이 있습니다.
또한 두번째로 weight의 갯수가 class number가 작은 경우에는 괜찮지만 class가 많아지게 되면 overfitting 문제가 발생하기 쉽다고 합니다.
결국 Fully Connected Layer는 지역적 연결성(local connectivity)와 weight 수에 따른 overfitting 문제가 있다는 점을 알고 넘어가시면 됩니다.

Convolutional Neural networks
이제 Convolutional Neural Networks (CNN) 에 대해서 배워봅시다.
아래 그림은 CNN의 기본 구조입니다.

이제 CNN에 기본적인 구조를 알아봅시다.
CNN은 아래와 같이 기존에 이미지 모습 그대로 입력으로 사용합니다.
CNN 에서 이미지의 크기를 이야기할때 width x height x channel 순서로 부릅니다.
또한 CNN에서는 weight를 filter라는 이름으로 부릅니다.
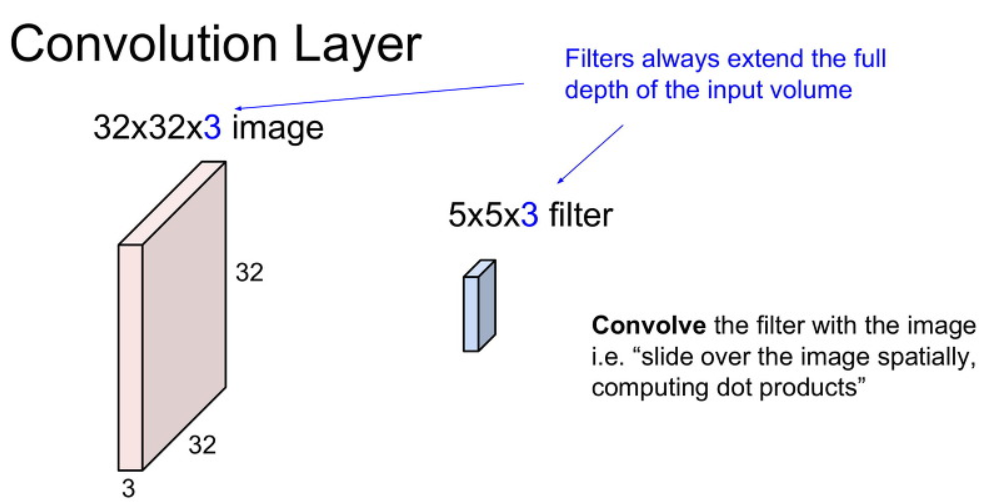
filter의 한 변의 크기는 image의 width와 height의 크기보다는 작은 값을 가집니다. 아래 그림 예시와 같은 경우 5 x 5 입니다.
filter의 depth 크기는 입력의 channel의 갯수와 같습니다. 결국 최종적인 filter의 크기는 5 x 5 x 3입니다.
여기서 filter의 depth 는 입력의 channel의 갯수와 같아야 한다는 점만 알아가시면됩니다.
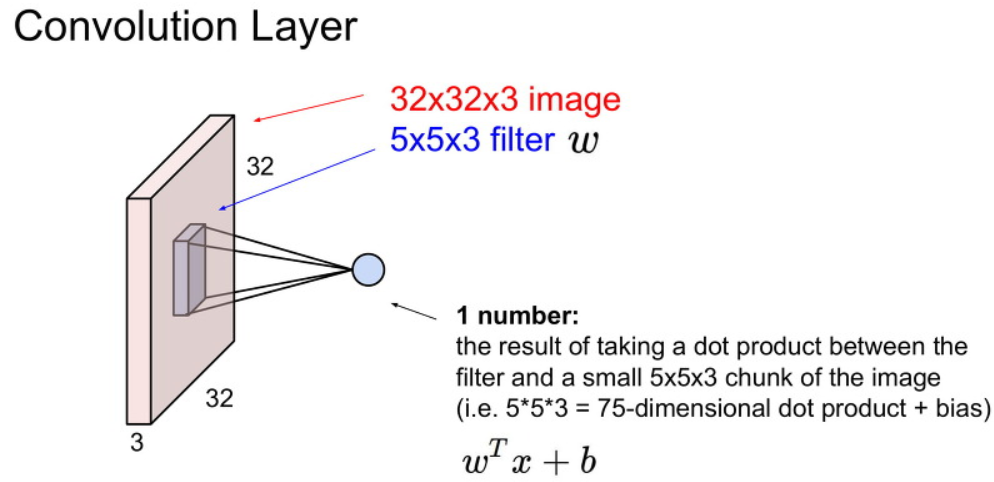
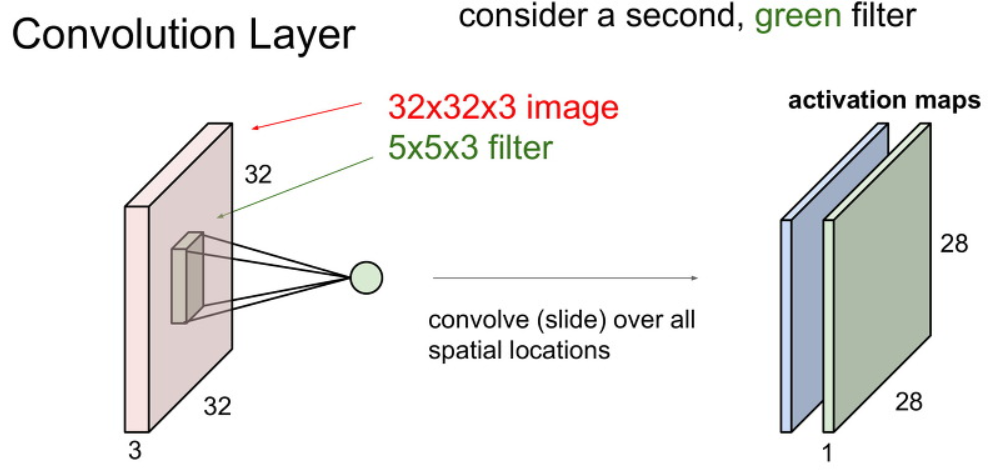
이제 왼쪽 위 모서리부터 필터가 image를 슬라이딩하면서 filter가 씌어진 부분은 dot product합니다.
그냥 filter가 씌어진 부분 끼리 각각 곱한 뒤에 모두 더한 값에 bias을 더한 값을 출력 값으로 사용합니다.
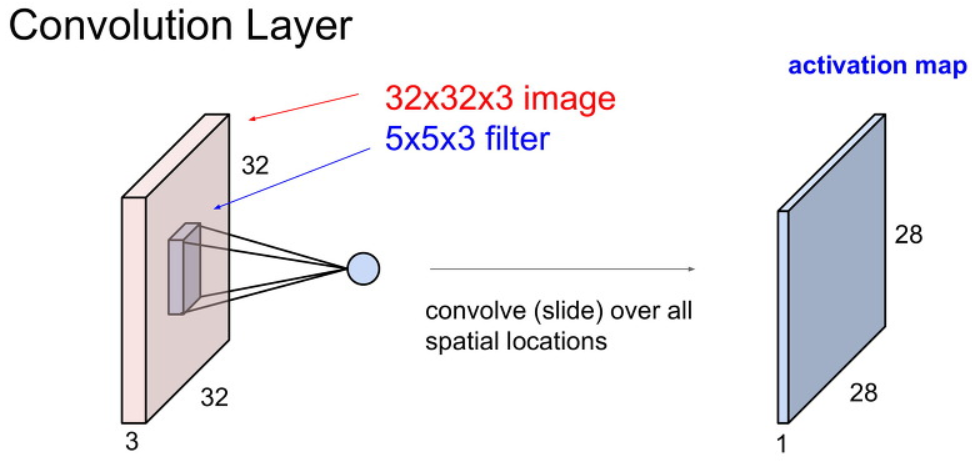
위와 같이 이미지를 filter로 쭉 슬라이딩하면 1개의 activation map이 생성됩니다.
activation map의 크기가 왜 28 x 28이 되었는지는 이후에 다루도록 하겠습니다.
CNN을 사용할 때에는 filter를 하나만 사용하지는 않습니다.
다양한 필터를 사용하며 필터마다 다른 특징을 나타내게 만드는 것입니다.
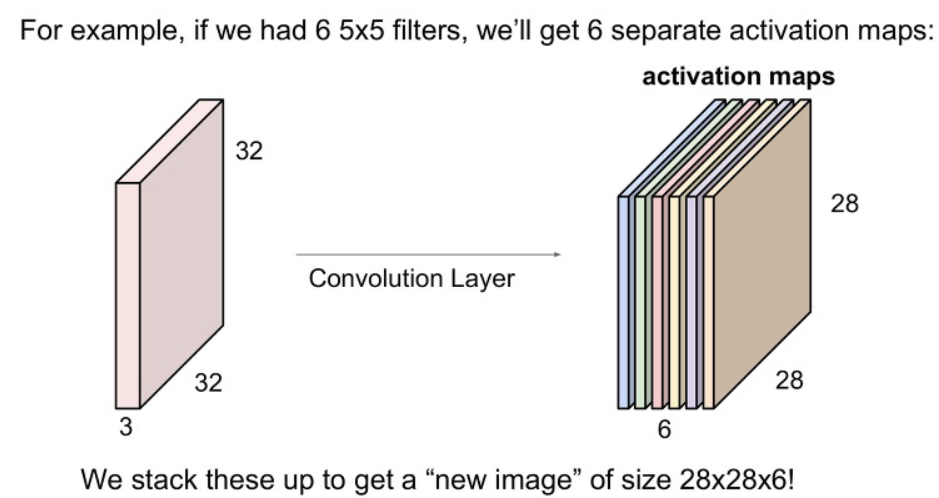
예를 들어 아래와 같이 6개의 필터를 사용하면 6개에 각각의 activation map을 형성하게 됩니다.
그리고 이것을 쌓아본다면, 우리는 28 x 28 x 6 크기의 output을 얻게 됩니다.
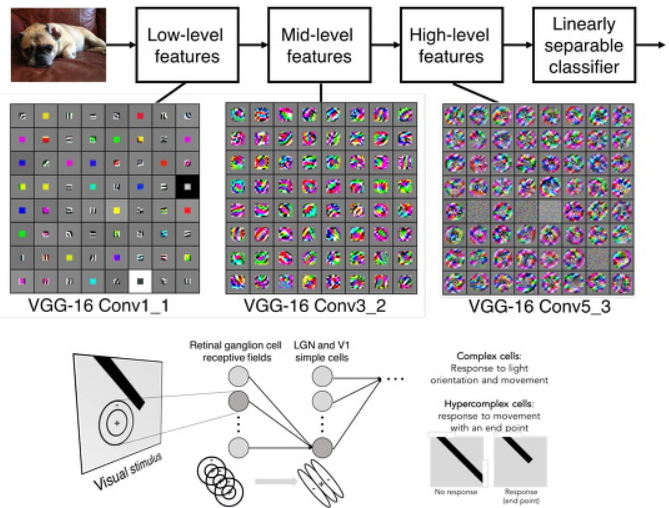
위에서 배운 Convolutional Layer을 여러개 이어 붙혀서 사용합니다.
이 Convolutional Layer가 깊어지면 깊어질 수록 더욱 더 복잡하고, 정교한 특징들을 얻어내는 것입니다.
아래 그림은 Convolutional Layer에 계산과정을 보여줍니다.
Convolutional Layer에 출력 크기를 계산으로 구할 수 있습니다.
입력 이미지의 한변의 길이를 W, Filter 한변 길이를 F라고하면
Output_W = W - F + 1 이라는 간단한 수식으로 계산할 수 있습니다.
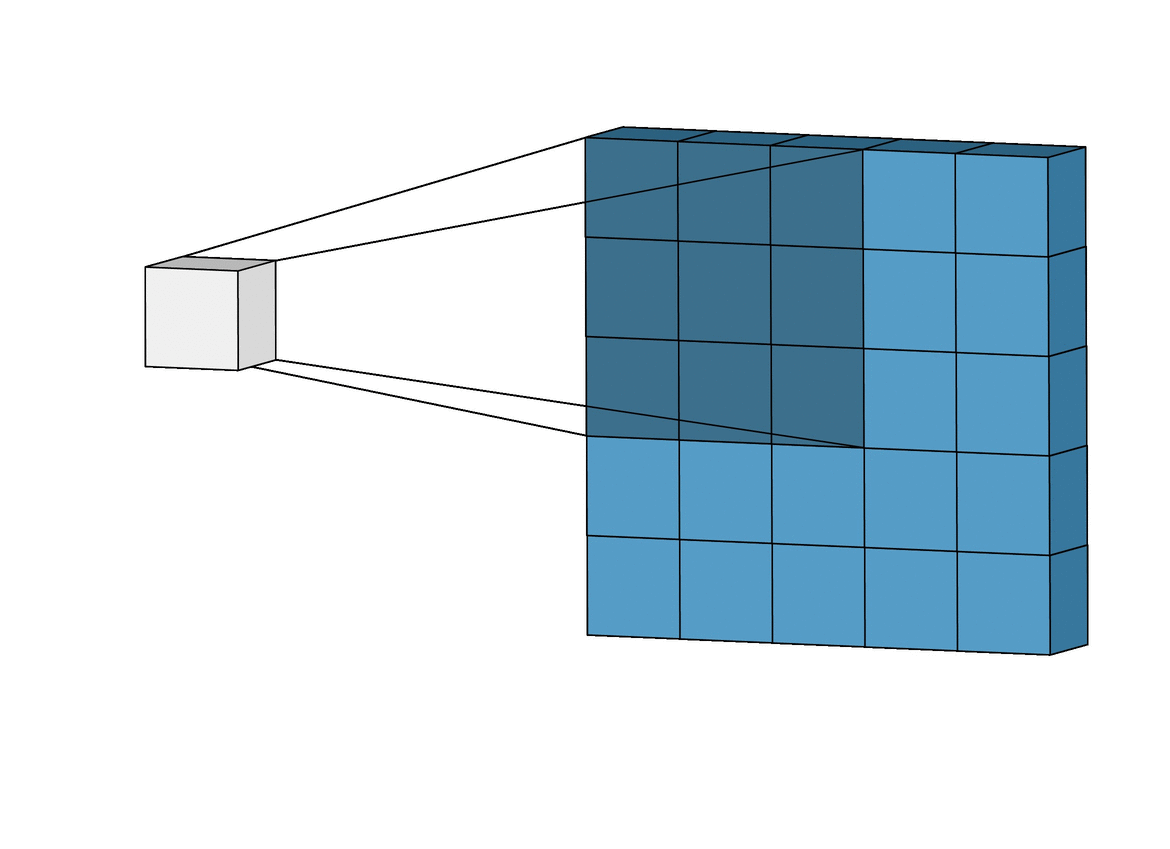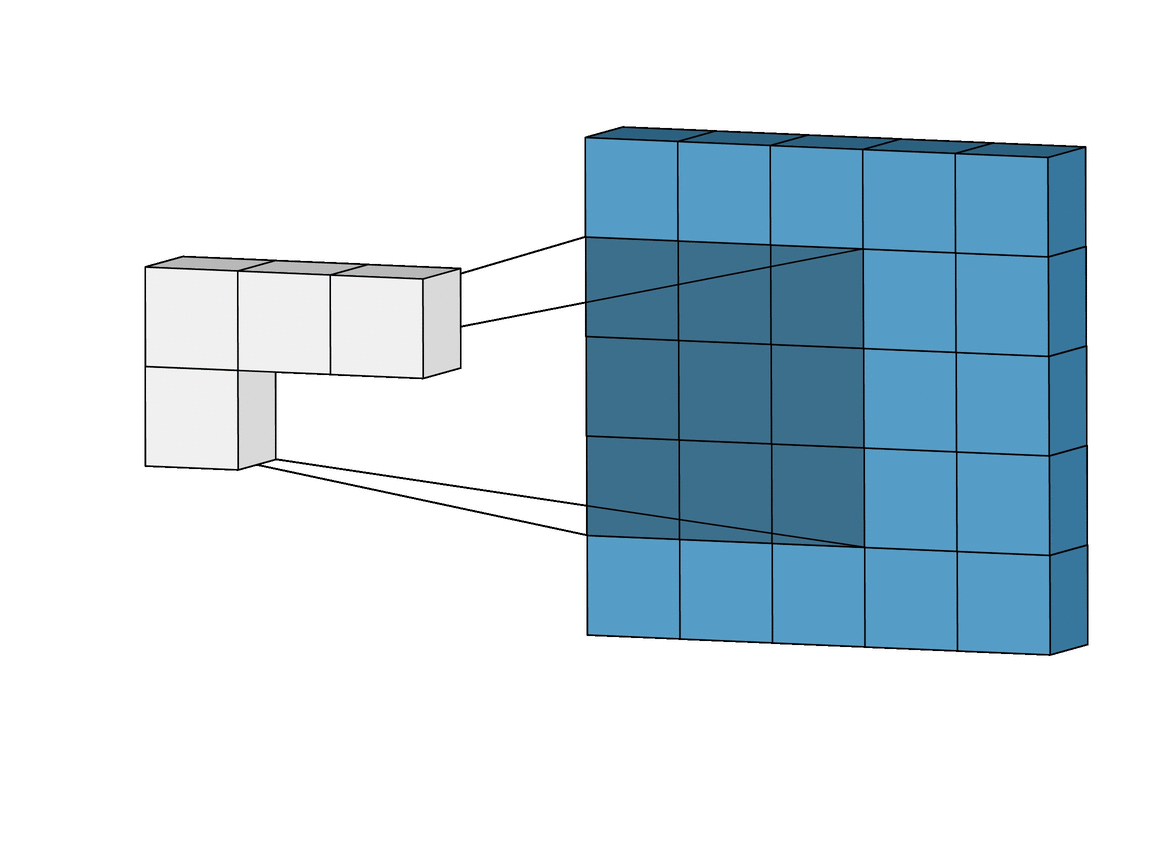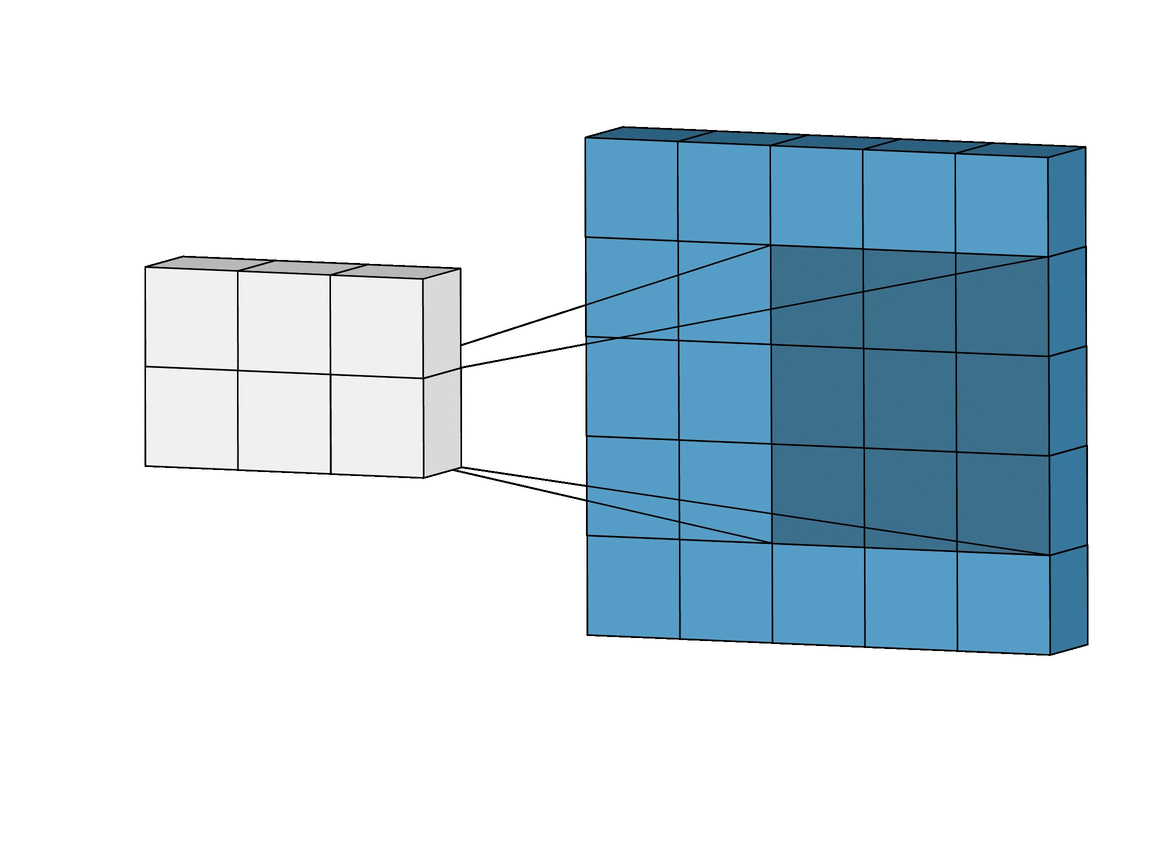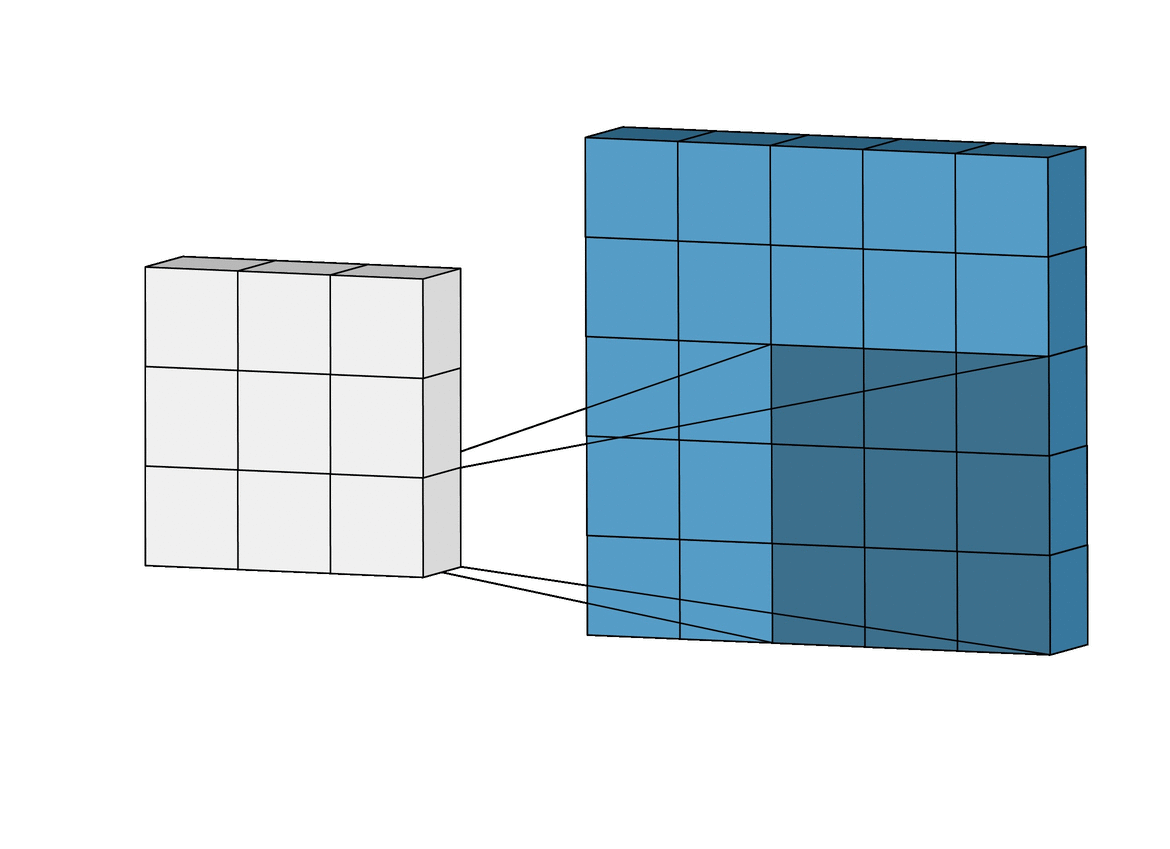
아래의 예시같은 경우 W = 5, F = 3 이므로 Output_W = 5 - 3 + 1 = 3로
아래 그림의 결과와 같은 것을 볼 수 있습니다.
이제 Convolutional Layer에서 사용하는 몇몇의 Hyperparameter에 대해서 배워봅시다
- Stride
- Pad
- Filter size (Width and Height)
- Output channel (Number of filter)
Convolutional Layer Stride
먼저 Stride에 대해서 설명하겠습니다.
Stride는 Filter가 이미지를 슬라이딩 할때 움직이는 step의 크기를 말합니다.
위에서 보여지던 Convolution 과정은 Stride가 1인 경우 였습니다.
아래와 같은 경우 Stride 크기가 2인 경우를 보여줍니다.

Convolutional Layer Pad
Convolutional Layer는 Filter에 크기에 따라서 출력의 가로와 세로의 길이가 줄어드는 것을 볼 수 있었습니다.
일반적으로 Convolution Layer을 1개가 아닌 여러겹으로 쌓아서 사용하기 때문에 이미지의 크기가 점점 줄어들게 됩니다.
이것은 이미지의 원본 크기를 유지할 수 있으며, 이미지의 가장자리가 덜 계산 되는 것을 방지합니다.

이제 각 모든 input channel 에 대해 곱해진 결과값을 모두 더합니다.
Convolutional Layer Output Size
위에서 배운 2가지 요소를 추가적으로 사용하여 출력 크기의 식은 아래와 같습니다.
W: input image widthF: Filter widthS: StrideP: PadOutput W:(W - F + 2*P)/S + 1

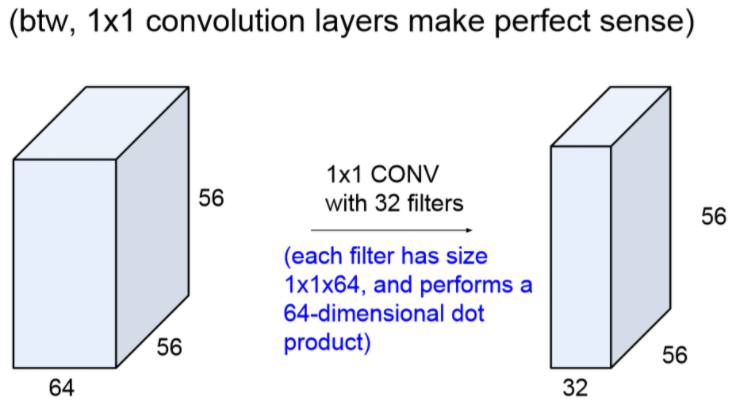
아래 그림은 1 x 1 CONV의 관련된 내용입니다.
기존에 사용하던 Filter와 다르게 width와 height값이 1인 경우입니다.
이러한 경우 Fully Connected Layer 대신에 1 x 1 CONV를 써도 무관하며 연산 결과 또한 같습니다.
Convolution Layer의 특징
지역적 연결성(local Connectivity)- Fully Connected Layer와 다르게 입력 값에 주변의 로컬한 영역에 연결한다는 장점이 있습니다.
- 깊이에 대해서는 전체를 다 봅니다.
공간적 배치(Spatial arrangement)- 출력의 크기는 4개의 하이퍼파라미터로부터 결정됩니다.
- 앞에서 살펴본 Filter의 사이즈(F), Stride(S), zero-padding(P), filter의 개수(K)입니다.
- 아래의 예시를 봅시다.
- 이 예제는 가로/세로 공간적 차원중 하나만 고려했습니다 (x축).
- 첫번째 예시는
W=5, F=3, S=1, P=1인 경우입니다. - 두번째 예시는
W=5, F=3, S=2, P=1인 경우입니다. - 위 두 예시와 같이 파라미터에 따라서 출력의 크기가 정해집니다.
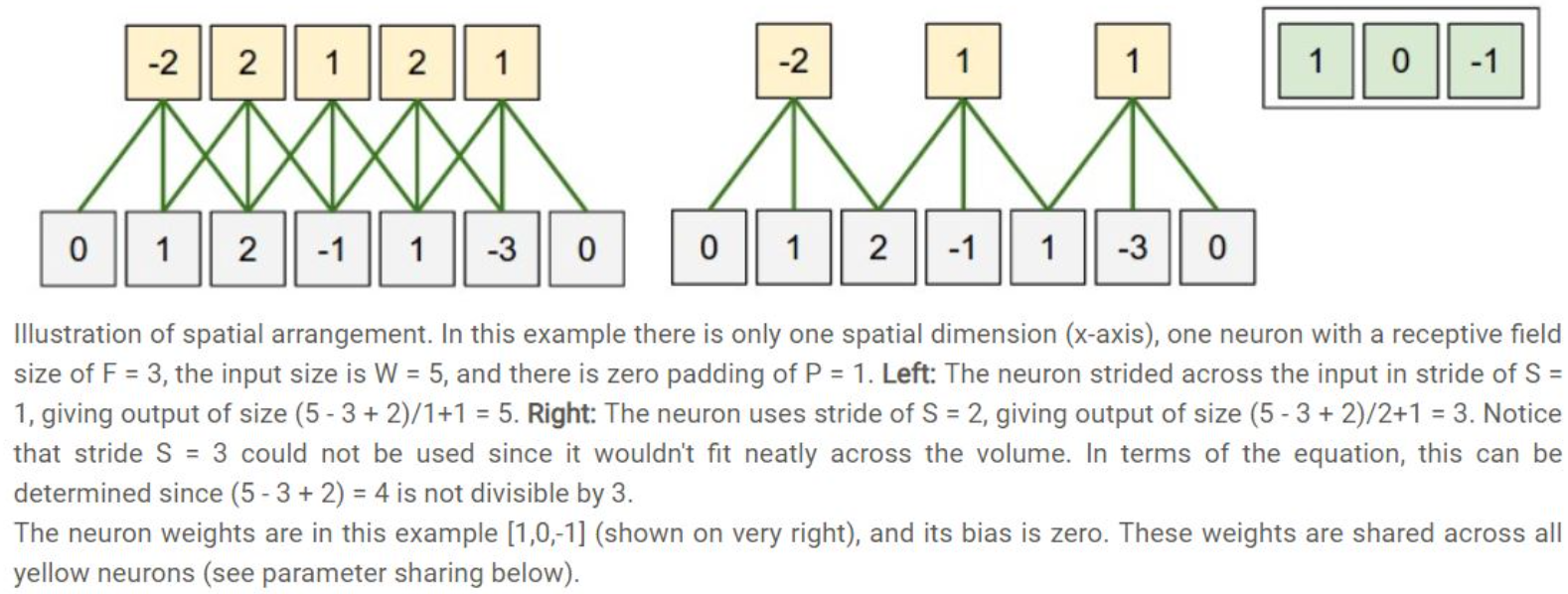
모수 공유(Parameter Sharing)- 각 채널에 대해서 하나의 filter를 사용하여 parameter를 공유한다는 이야기입니다.
- 이러한 점은 parameter의 수를 줄일 수 있습니다.
Convolution Layer의 Backpropagation
backpropagation 과정에서 각 depth slice 내의 모든 뉴런들이 가중치에 대한 gradient를 계산하겠지만, 가중치 업데이트를 할 때에는 이 gradient들을 합해 사용합니다.
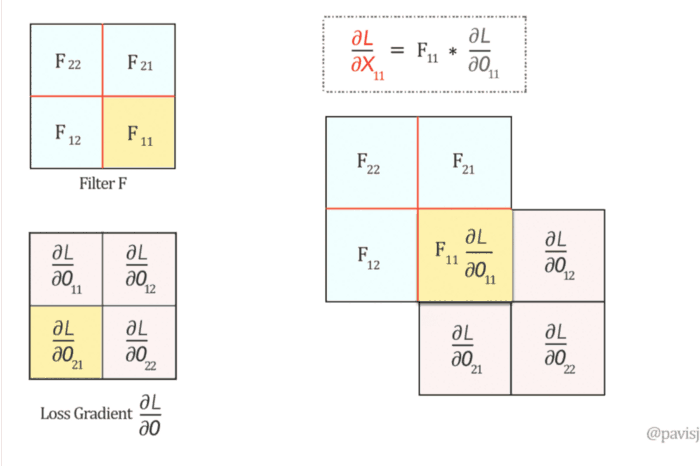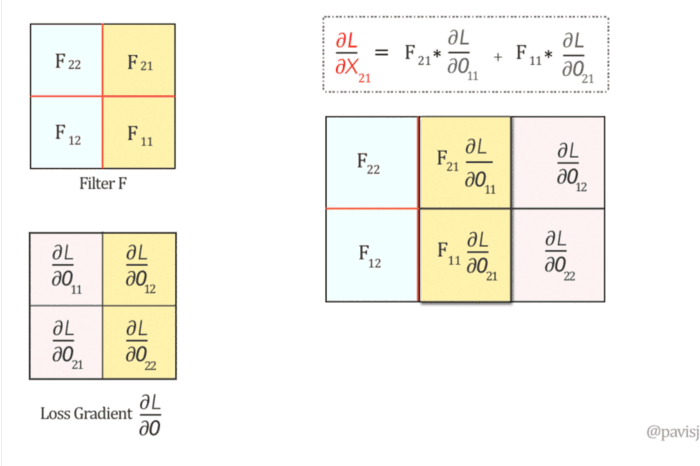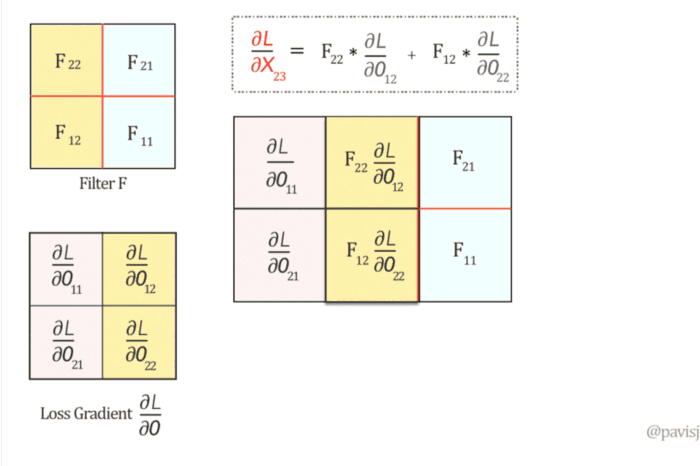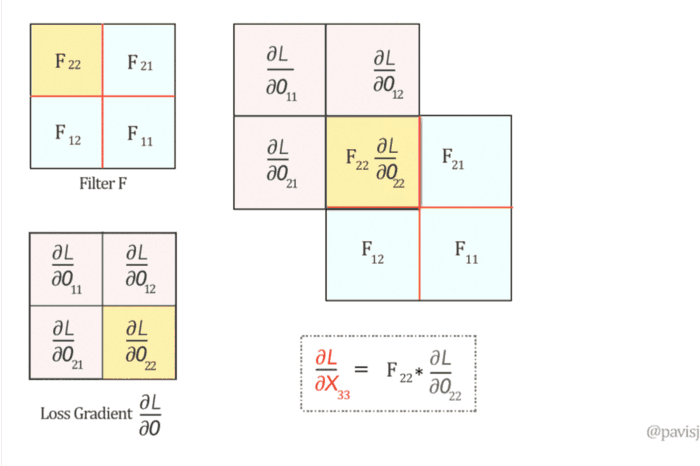
CNN Architecture
Layer Pattern
TAEU 님의 블로그 내용을 그대로 인용했습니다.
큰 크기의 필터 Conv 레이어보단, 여러 개의 작은 사이즈의 필터를 가진 Conv 레이어를 쌓는 것이 좋다.
-
예시
-
작은 3x3 크기 필터의 receptron filed
3x3 크기의 CONV 레이어 3개를 쌓는다고 생각해보자. 물론 각 레이어 사이에는 비선형 함수를 넣어준다.
첫 번째 CONV 레이어의 각 뉴런은입력 볼륨의 3x3영역을 보게 된다.
두 번째 CONV 레이어의 각 뉴런은 첫 번째 CONV 레이어의 3x3 영역을 보게 되어 결론적으로입력 볼륨의 5x5영역을 보게 되는 효과가 있다.
세 번째 CONV 레이어의 각 뉴런은 두 번째 CONV 레이어의 3x3 영역을 보게 되어입력 볼륨의 7x7영역을 보는 것과 같아진다. -
큰 filter와 작은 filter 간의 차이점
하지만 단순히 7x7 filter만 쓰게되면 몇 가지의 단점이 생긴다. 3x3 3개의 conv 레이어는
중간에 비선형함수(activation function)을 넣게되어 좋은 feature를 만들 수 있는 반면, 7x7 짜리 필터를 가지는 conv 레이어는단순히 선형 결합이다. 따라서 전자가 더 좋은 특징들을 만들 수 있다. 또파라미터 개수를 비교해보면 (모두 K개의 커널(혹은 depth)를 가진다고 할때), 전자는 3개의 레이어x (K x (3 x 3 x K)) = 27K^2, 후자는 1개의 레이어x (K x (7 x 7 x K)) = 49K^2이다. 하지만, 학습 시에는 중간의 결과물들을 저장해야할 결과물들이 여러 레이어를 쌓는 것에 비해 메모리를 적게 사용한다는 장점은 있다.
-
Pooling Layer
Pooling은 activation map의 크기를 downsampling 하는 과정을 이야기합니다.
즉 이미지의 크기를 줄이는 것이죠.
Convolutional Layer의 깊이가 깊어지면 많은 계산 양을 요구합니다.
이때 Pooling 기법을 이용해서 이미지의 크기를 줄여서 속도를 높이고자 합니다.
이미지를 줄이는 방법은 위에서 Convolutional layer의 Stride를 이용해서도 줄일 수 있습니다.
Pooling 기법이 계산량과 weight의 수 측면에서 더 좋습니다.

Max Pooling Layer
Pooling의 가장 대표적인 방법으로 Max Pooling 이란 것이 있습니다.
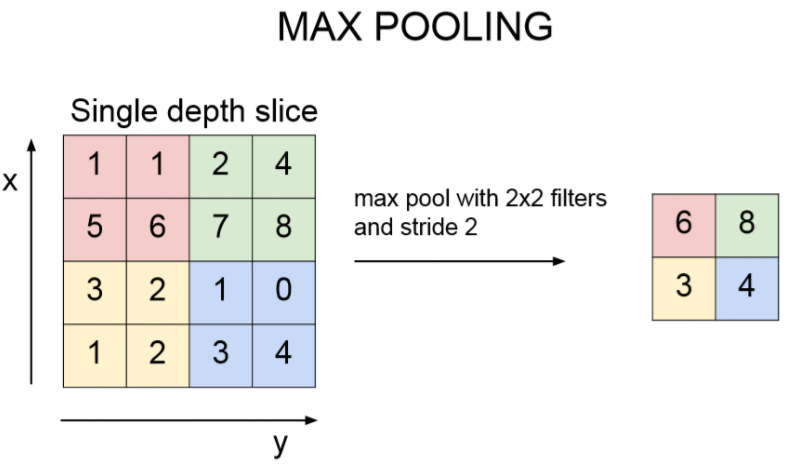
아래 그림은 4 x 4 입력 이미지를 2 x 2 filter로, stride는 2로 pooling 합니다.
그리고 나서 filter에 convolution 하듯이 MAX 연산을 해줍니다.
이렇게 하면 해상도를 2배로 줄일때 가장 잘보이는 성분을 남기는 것과 같습니다.
여기서 일반적으로 stride를 설정할때는 filter끼리 서로 겹치는 것을 지양합니다.
또한 이 Max Pooling를 사람의 뉴런 관점에서 생각할때, 가장 큰 신호만 전파시키는 방식이라고 생각할 수도 있다고 합니다.
Max Pooling Layer Backpropagation
Backpropagation 챕터에서 max(x,y)의 backward pass는 그냥 forward pass에서 가장 큰 값을 가졌던 입력의 gradient를 보내는 것과 같다고 배운 것을 기억합시다.
그러므로 forward pass 과정에서 보통 max 액티베이션의 위치를 저장해두었다가 backpropagation 때 사용합니다.
Pooling vs Conv Stride
풀링 레이어가 보통 representation의 크기를 심하게 줄이기 때문에 (이런 효과는 작은 데이터셋에서만 오버피팅 방지 효과 등으로 인해 도움이 됨), 최근 추세는 점점 풀링 레이어를 사용하지 않는 쪽으로 발전하고 있다고 합니다.
본질적으로 max-pooling(또는 어떤 종류의 pooling)은 고정된 연산이며 이를 strieded convolution으로 대체하는 것도 pooling 연산을 학습하는 것으로 볼 수 있어 모델의 표현력이 높아집니다. 부정적인 측면은 훈련 가능한 매개변수의 수 또한 증가한다는 것이지만, 이것은 이 시대의 진정한 문제는 아닙니다.
또 이와 관련되어 JT Springenberg 에서 발표한 좋은 기사가 있습니다.
이전에 Max Pooling를 사용하여 사용하던 것을 모두 strided-convolution 으로 바꾸어 보았는데, strided-convolution이 max-pooling보다 좋은 성능을 가졌다고 합니다.
There is a very good article by JT Springenberg, where they replace all the max-pooling operations in a network with strided-convolutions. The paper demonstrates how doing so, improves the overall accuracy of a model with the same depth and width: "when pooling is replaced by an additional convolution layer with stride r = 2 performance stabilizes and even improves on the base model"
결론
- CONV 의 계산 과정을 이해한다.
- CONV 의 사용 이유와 장점을 이해한다.
- Pooling과 FC layer에 대한 내용을 이해한다.
다음 내용
- activation function, initialization, dropout, batch normalization 에 대해서 배우겠습니다.