소개
- 이 글은 단지 CS231n를 공부하고 정리하기 위한 글입니다.
- Machine Learning과 Deep Learning에 대한 지식이 없는 초보입니다.
- 내용에 오류가 있는 부분이 있다면 조언 및 지적 언제든 환영입니다!
참조
개요
< Image Classification >
-
2-1) Nearest Neighbor
Image Classification 소개
Image Classification 이란 말 그대로 이미지를 입력으로 받아 이를 분류하는 것을 말합니다.
사람에게는 이러한 이미지 분류가 쉬워 보이지만 컴퓨터에게는 생각보다 어려운 작업입니다.
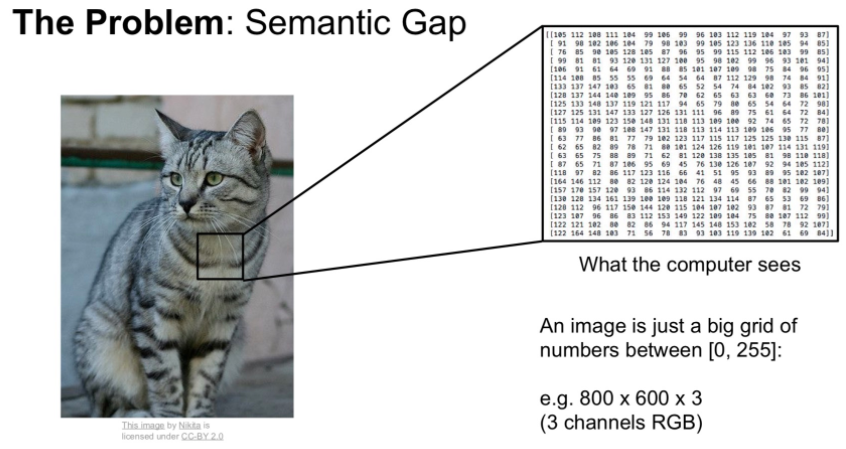
아래 그림은 컴퓨터가 그림을 바라보는 관점을 보여줍니다.
우리가 보기에는 고양이의 그림이지만, 컴퓨터에게는 그저 숫자의 집합입니다.
또한 고양이의 자세, 카메라의 각도, 빛의 세기 등 과 같은 작은 변화에 숫자 값들은 민감하게 반응하며 우리는 이러한 다양한 상황을 이겨낼 수 있는 "확장성"을 가진 이미지 분류 알고리즘을 찾아야합니다.
우리는 이러한 것을 해결하는 방법으로 "데이터 중심 접근방법(Data-Driven Approach)" 에 대해 알아보도록 합시다.
Data-Driven Approach
Data-Driven Approach 란 단순히 한 사진 만을 가지고 결정을 하는 것이 아니라 무수히 많은 사진들과 그 사진에 대한 정보 를 이용하여 이미지 분류기를 만들고 새로운 사진에 대해 분류하는 접근방식을 말합니다.
이러한 접근방식을 위해서 먼저 필요한 것은 다음과 같습니다.
1. 데이터 셋 (Dataset)
2. 데이터 학습 (Train)
3. 데이터 판단 (Predict)
"데이터 셋(Dataset)" 이란 무수히 많은 데이터 뿐 아니라 각 데이터에 대한 정보를 나타내는 라벨(Label) 이 함께 달린 데이터를 말합니다.
"데이터 학습(Train)" 이란 새로운 이미지를 판단하기 위해 데이터 셋을 이용하여 미리 분류기를 만들고 학습하는 과정을 말합니다.
"데이터 판단(Predict)" 이란 위에서 학습된 분류기를 이용하여 새로운 이미지에 대해 판단, 분류 및 예측을 하는 과정입니다.
이제 어떻게 데이터를 이용하여 분류기를 만드는지 소개하도록 하겠습니다.

먼저 가장 간단하고 기본적인 분류방법인 Nearest Neighbor(NN) 를 먼저 다루도록 하겠습니다.
"Nearest Neighbor(NN)" 이란 즉 "가장 가까운 이웃 찾기"입니다.
이는 정말 직관적인데 새로운 이미지와 이미 알고 있던 이미지 를 비교하여 가장 비슷하게 생긴 것을 찾아 내는 것 을 말합니다.

이러한 작업을 하기 위해서는 다음과 같은 작업이 필요합니다.
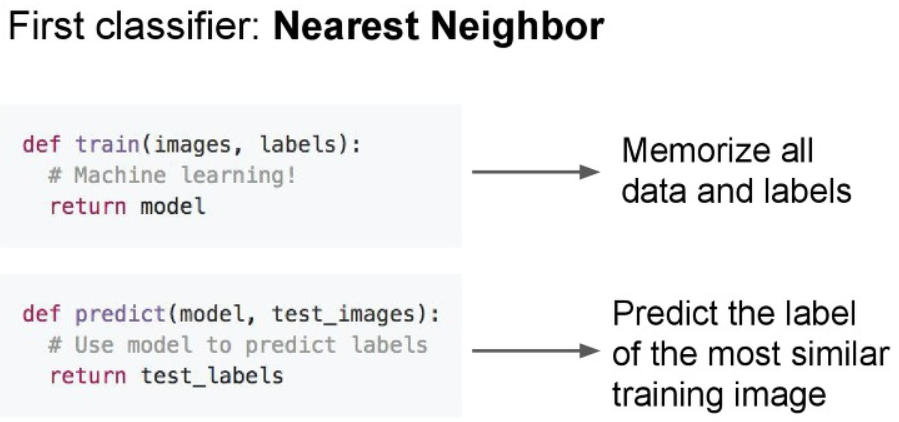
1. 데이터 학습(Train)
+ NN 에서는 Train에서는 나중에 새로운 이미지와의 비교를 위해 단순히 이미지를 저장합니다. O(1)
2. 데이터 판단(Predict)
+ Train에서 가지는 학습 된 이미지와 새로운 이미지와 가장 비슷한 이웃을 찾고 그에 따라 분류합니다. O(N), N: 학습된 데이터의 총 개수
+ 주변 이웃인지 판단하는 방법은 뒤에서 더 다루도록 하겠습니다.
@문제점
- 이미 알아보신 분도 있겠지만, 데이터 학습은 빠르지만, 새로운 데이터를 판단하는데 있어서 걸리는 시간이 많이 필요합니다.
- 이 분류기가 언듯보기에 쓰지 않을 것을 왜 알아야 하지? 에 대한 의문을 가질 수 있을 것입니다. 하지만 이는 머신러닝의 기초가 되는 내용 알아가기에 좋은 예 로 한번 살펴 보도록합시다.
K-Nearest Neighbor 소개
아래 그림은 위에서 보여준 Nearest Neighbor의 한 예입니다.
이래 그림을 보면 초록색 부분에 한개의 노란색이 존재하는 것을 볼 수 있습니다.
이러한 1개의 노란색으로 저렇게 판단하는 것이 과연 좋은 선택일까요?
이러한 것은 오히려 새로운 데이터에 대해서 좋지 않은 결과를 가져을 수 있습니다.
이러한 점에서 이제 K-Nearest Neighbor(KNN) 에 대해 다룰 것입니다.

K-Nearest Neighbor(KNN) 은 가까운 이웃을 K개 만큼 찾고, 이웃끼리 투표를 하는 방법입니다.
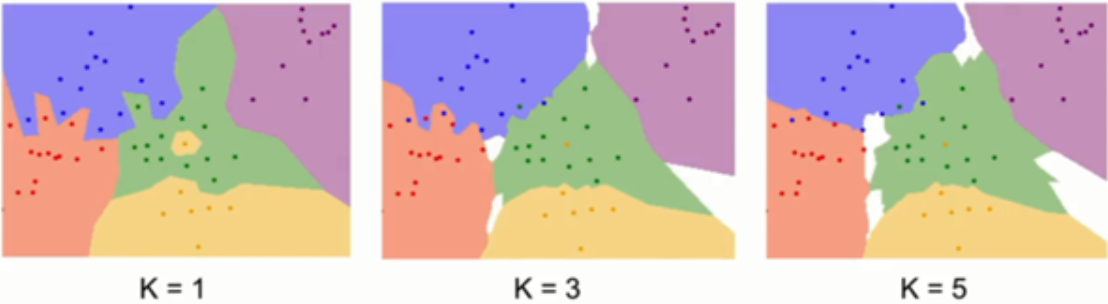
아래 그림을 보면 K 값이 증가함에 따라서 경계가 점점 부드러워 지고 있는 것을 볼 수 있습니다.
이러한 방식을 이용하면 좀 더 일반화 된 결정 경계를 찾을 수 있습니다.
여기서 K값의 증가함에 따라서 부드러워 지지만, 흰색 영역이 증가 하는 것을 볼 수 있습니다.
이 흰색 영역 은 어느 쪽에도 분류 할지 알 수 없는 영역입니다.
이러한 부분에서 K값이 증가한다고 항상 좋은 것이 아니라. 데이터나 상황에 따라서 알맞은 K값을 찾아야합니다.
Distance Matrix
우리는 아직까지 어떻게 가까운 이웃을 찾아내는지 알지 못합니다.
이 KNN 알고리즘에서 가까운 이웃을 찾아내는 방법으로 아래와 같은 Distance Matrix를 사용합니다.
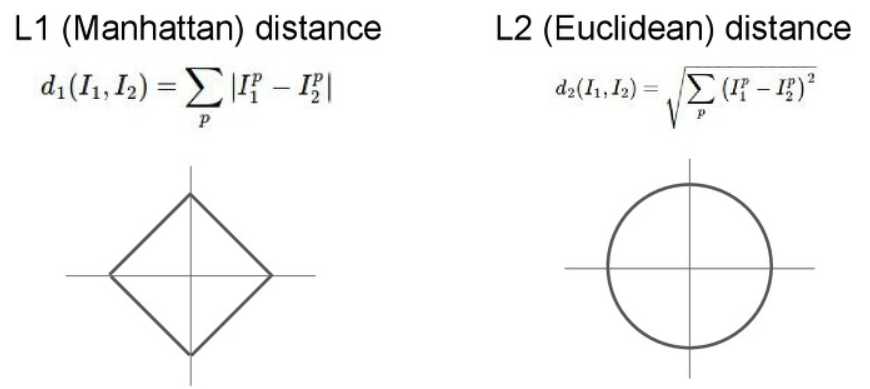
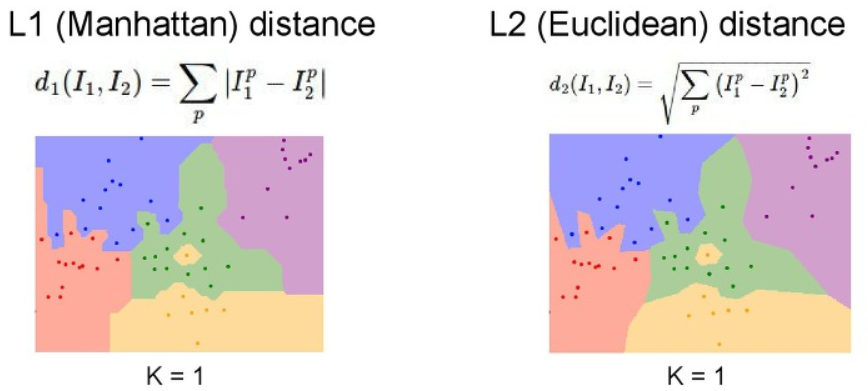
Distance Matrix은 데이터 간에 거리를 측정하는 방법으로 크게 L1과 L2 방식으로 나누어집니다.
L1은 각 성분의 차이를 모두 더한 것이며, L2는 유클리드 거리를 사용합니다.
이 두가지 방법에 차이를 음미하면 다음과 같습니다.
-
L1의 특징
- 기존의 좌표계를 회전하면 거리가 바뀝니다.
- 각 성분이 개별적인 의미 를 가지고 있을 때 L1이 어울립니다.
- 예시) 키, 몸무게
-
L2의 특징
- 위와 다르게 회전에도 거리가 변하지 않습니다.
- 일반적인 벡터이며, 요소들간의 실직적인 의미가 없는 경우 사용합니다.
-
L1과 L2의 결정
- 사실적으로 데이터의 성분 관계를 정확하게 알지 못하는 경우가 대부분입니다.
- 이를 정하는 것은 깊게 생각하지 말고, 둘다 사용해보고 성능이 더 좋은 것을 사용합시다.
ex) 각각 L1과 L2를 사용한 NN의 결과이다.
Hyperparameter
자 위에서 배운 KNN을 보면 K, Distance Matrix와 같이 우리가 직접 정해 주어야 하는 값 들이 있습니다.
이처럼 우리가 직접 정해주어야 하는 값을 Hyperparameter(초모수) 라고 합니다.
이러한 Hyperparameter의 값은 상황에 따라서 다른 값을 가지므로 이를 찾아가는 과정이 필요합니다.
이러한 Hyperparameter를 찾아가는 일반적인 방법을 소개하고자 합니다.
Hyperparameter 설정 방법
자 우리에게 어떤 데이터셋(Dataset)이 주어졌다고 생각합시다.
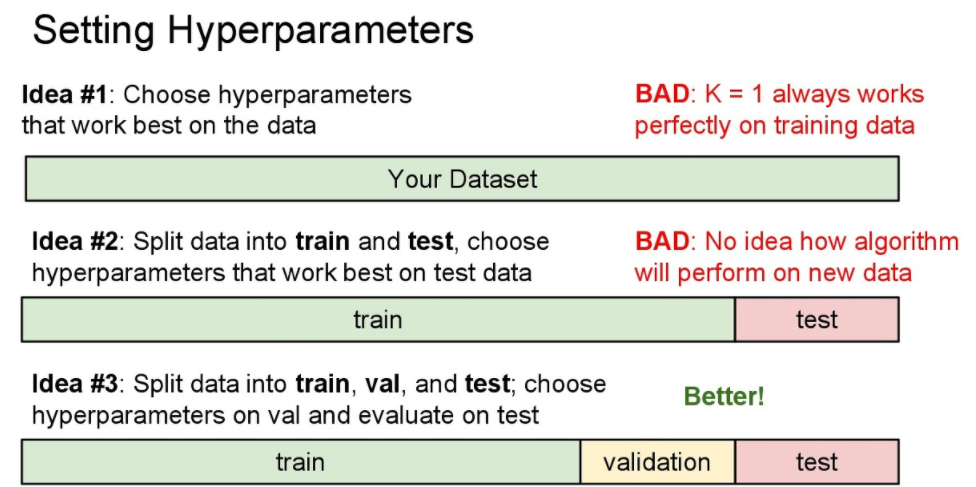
아래 그림에서는 이러한 데이터셋을 사용하는 방법 3가지 를 소개한다. 한번 살펴봅시다.
-
Idea #1: 모든 데이터를 Train 으로 사용하는 방법
- 우리는 주어진 데이터에서 좋은 성능을 가지는 것보다 새로운 데이터 들에 대해 높은 정확도 를 가져야 합니다.
- 모든 데이터를 사용하는 경우 KNN에서 K=1인 경우 Train set에 대해 가장 좋은 결과를 가지지만, 새로운 데이터에 대해서는 그렇지 않습니다.
-
Idea #2: 데이터를 Train과 Test 로 나누는 방법
- 그럼 Train과 Test로 나누어서 사용해볼까요?
- Train 데이터를 이용해서 Test 데이터가 정답인지 아닌지 확인합시다.
- 이제 K값을 바꾸어 가면서 이중에 가장 높은 성능을 가지는 K값을 찾으면 되겠습니다!
- 하지만 이 방법은 이 Test 데이터에 대해서만 좋은 결과 값을 가질 수 도 있습니다.
- 우리는 실제로 보지 않은 데이터에 대해서 좋은 성능을 평가 해야 합니다.
-
Idea #3: 데이터를 Train, Validation(Dev), Test 로 나누는 방법
- 이제 우리는 validation를 추가로 사용할 것입니다.
- 이제 Train를 한 뒤에 이 Validation를 이용하여 좋은 성능을 가지는 Hyperparameter를 찾을 것 입니다.
- 이 Validation에서 좋은 성능을 가지는 Hyperparameter를 찾은 뒤 에 마지막에 딱 한번 Test 데이터를 테스트 하여, 이 데이터를 최대한 "Unseen Data"로 활용하는 방법 입니다.
- 위 방법들 중 이 방법이 제일 올바른 방법 입니다.
Cross-Validation
위에서 Hyperparameter를 찾는 3가지 방법을 배웠습니다.
위 3가지 방법과 별개로 또 다른 방법인 Cross-Validation를 소개하고자 합니다.
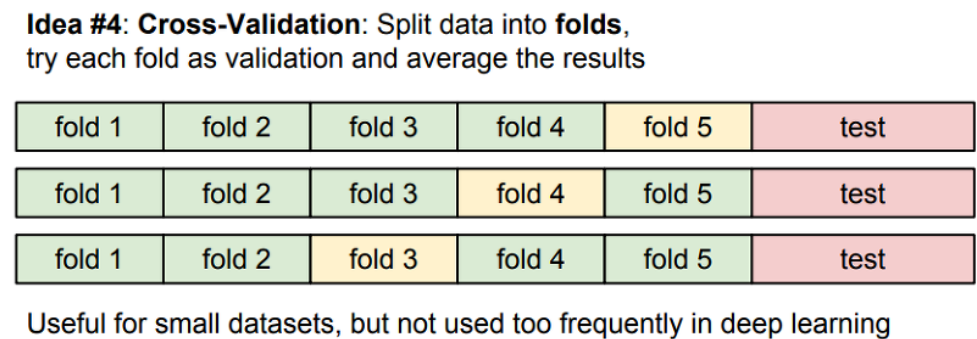
Cross-Validation 은 아래 그림과 같이 Dataset를 Fold 단위로 자르고, 이 fold 중 하나를 validation으로 선택하고 나머지를 train 데이터로 사용 합니다.
위 방법으로 Validation으로 사용할 fold를 바꿔가면서 반복 하고, 이중에 가장 좋은 성능을 가지는 Hyperparameter를 찾아내는 방법 입니다.
이 방법은 validation의 데이터가 편향되는 현상을 방지할 수 있습니다.
기존에 방식보다 많은 학습시간 을 요구하며 이 방법은 거의 사용되지 않고 데이터가 적은 상황에서 유용한 장점을 가집니다.
Hyperparameter 예시
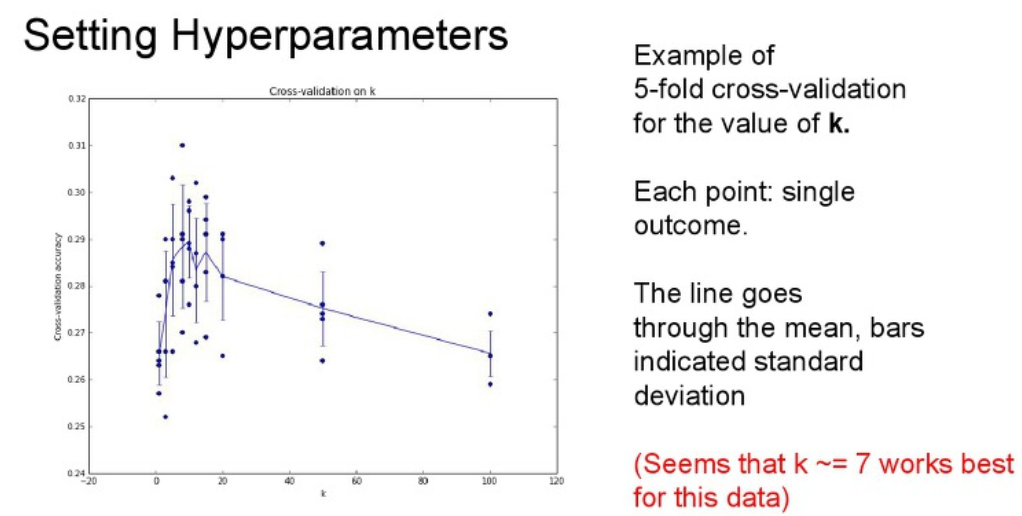
이 예시는 5-fold cross-validation를 이용하여 학습한 결과입니다.
아래 왼쪽 그래프는 가로축은 K값을, 세로축은 성능을 나타냅니다.
성능은 K값이 7일때 가장 좋은 성능을 보이는 것을 볼 수 있습니다.
하지만 이것이 항상 K가 7일때 좋은 결과를 가진다는 것이 아닙니다.
데이터셋의 종류, 찾는 문제에 따라서 이것은 다시 구해져야합니다.
이미지의 Distance 의미
하지만 지금까지 열심히 공부한 Nearest Neighbor 은 이미지에서 절대로 사용되지 않습니다.
우선 초반에 언급한 predict과정이 오래 걸린다는 것과, 사진 간에 distance 값이 그렇게 의미있는 값이 아니기 때문입니다.
아래 예시를 봅시다.
아래에는 가장 왼쪽에 원본 이미지와 변형된 3개의 이미지를 보여줍니다.
여기서 재밋는 부분은 원본사진과 각각의 사진에 거리가 모두 같은 사진입니다.
이러한 관점에서 이미지의 Distance의 값은 그렇게 의미 있는 값이 아닙니다.

Curse of dimension
Curse of dimension(차원의 저주) 란 KNN이 잘 작동하기 위해서는 전체 공간을 조밀하게 커버할 수 있을 정도의 데이터가 필요하다 는 이야기입니다.
여기서 Curse of dimension 이란 아래 그림과 같습니다.
-
1차원 에서는 4개의 데이터가 필요 했다면, -
2차원 에서는 4 * 4 = 16개의 데이터가, -
3차원 에서는 4 * 4 * 4 = 64개의 데이터가 필요하다.
이와 같이 고차원으로 갈 수록 기하급수 적인 데이터가 필요 합니다.
이 필요한 데이터가 4개라면 괜찮지만 10000개가 필요하다고 하면 실감할 수 있을 것입니다.

Linear Classification
자 이제 Linear Classification(선형 분류)라는 것을 알아봅시다.
Linear Classification 은 단순하지만 이후에 배우게 되는 Neural Network와 CNN의 기반이 되는 알고리즘입니다. 즉 아래 그림과 같이 기본 블럭이 되는 것입니다.

Parametric Approach
Linear Classification은 "Parametric model" 의 가장 기본적인 형태입니다.
Parametric model에는 두가지 성분이 있습니다.
- 가중치 값 (Weight Parameter) :
W - 편향 값 (Bias) :
b
위에 Parametric model 값을 단순하게 "Wx + b" 와 같이 선형적으로 사용하는 것을 바로 Linear Classification 이라고 합니다.
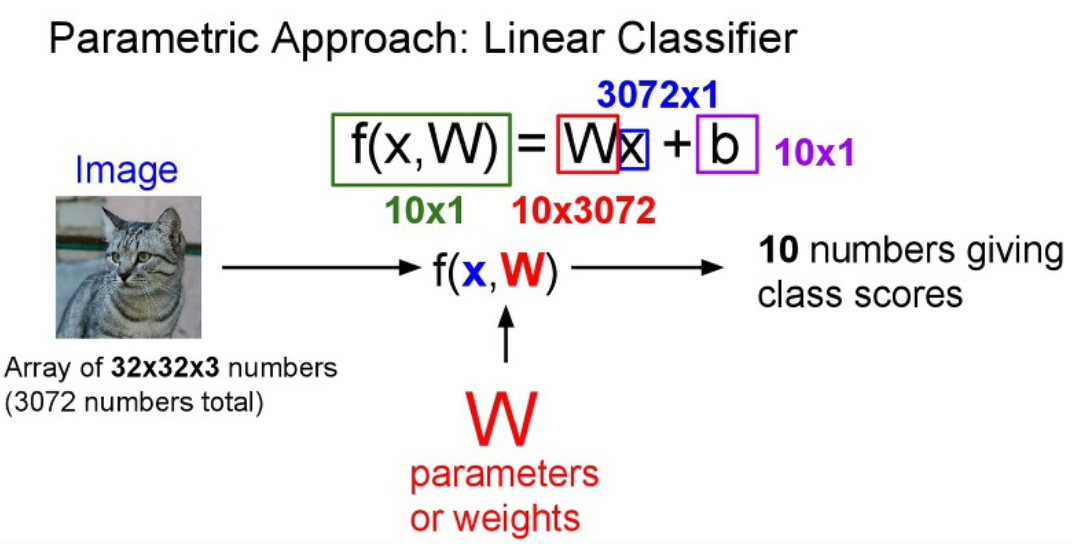
아래 그림에서는 기본적인 Linear Classification 예시를 보여줍니다.
-
X: 입력 ImageX의 크기 : 32x32x3 = 3072x1 크기를 가지는 고양이 사진을 사용합니다.
-
W: 가중치 값- 만약 분류할 동물의 클래스 수가 10개 라고 합시다.
- Dimension 크기를 맞춰주기 위해서
W의 크기 : 10x3072를 가집니다.
-
b: Bias 값- Bias(편향치)는 x와 W의 곱한 결과에 이 값을 더해줍니다.
Bias 크기: 10x1를 가지는 것을 볼 수 있습니다. (Class 갯수)- 이 Bias는 데이터와 무관하게 특정 클래스에 "우선권"을 부여합니다.
- 예) 데이터셋이 불균등한 상황 : 고양이 사진이 개 사진보다 많은 경우
Linear Classification 과정 예시
아래는 이해를 돕기 위한 Linear Classification의 한 예시입니다.
아래는 입력 이미지의 크기가 2x2=4 라고 가정했습니다.
분류할 카테고리는 3가지 (고양이/개/양) 이라고 합시다.
각 성분의 크기는 다음과 같습니다.
-
X: 입력 이미지X의 크기: 4x1로 1차원으로 폅시다.
-
W: 가중치 값(Weight Parameter)W의 크기: 3x4로 (클래스 갯수) x (입력 데이터 크기) 입니다.- 각 행(row)은 하나의 클래스를 담당 하므로 이를 템플릿으로 볼 수 있습니다.
- 여기서
W의 행 백터와 입력값 간에 내적을 계산하는데, 이것이각 클래스 간 템플릿의 유사도를 측정하는 것으로 볼 수 있습니다.
-
b: Bias 값Bias의 크기: 3x1로 (클래스 갯수) x 1 입니다.- 이 값은 독립적으로 각 클래스의 scaling offset 를 더해주는 것과 같습니다.

Linear Classification 해석 - Weight의 템플릿 값
아래 결과는 CIFAR-10 이라는 데이터셋을 이용하여 Linear Classification를 학습한 결과입니다.
가장 아래 보이는 10개의 그림은 각각 템플릿의 weight 값을 나타낸 것입니다.
이 weight 값은 각 class에 있는 모든 이미지를 평균화 시키므로 다양한 모습의 사진이 있지만 하나의 템플릿 값만 가집니다.
아래의 자동차(car)의 템플릿(weight)값을 보면 진짜 자동차와 같은 모습을 볼 수 있습니다.
하지만 말(horse)을 봅시다. 말은 데이터 속에 왼쪽,오른쪽 모습이 모두 있을 수 있어 이것이 겹쳐서 보입니다.

Linear Classification 해석 - 이미지를 고차원에서 하나의 점으로
또 다른 관점은 이미지를 고차원에서 하나의 점으로 생각하는 것입니다.
이러한 관점으로 Linear Classification을 해석하면 아래 그림과 같습니다.
W: 가중치 값 - 각 선분의 기울기b: Bias 값 - 선분의 시작 offset 값
이러한 관점에서 각 class은 선분을 가지며 이러한 선을 기준으로 분류 하는 것으로 해석할 수 있습니다.

Hard cases for a linear classification
이러한 Linear Classification으로 풀 수 없는 어려운 경우가 존재합니다.
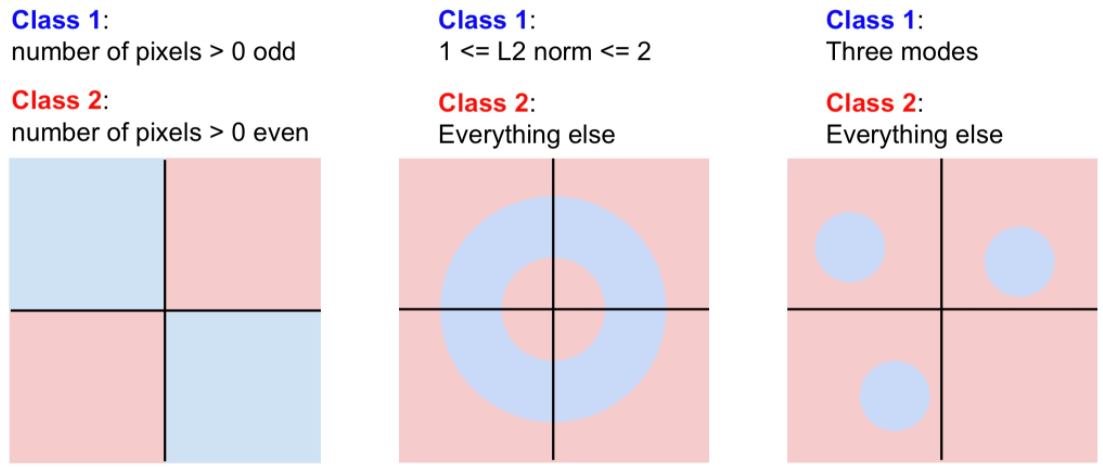
아래 그림은 Linear Classification으로 분류할 수 없는 경우를 보여줍니다.
각각은 Partity Problem(Xor), 도넛 형태, Multimodal Problem 입니다.
안타깝지만, 이러한 경우 Linear Classification 으로 풀 수 없는 문제입니다.
결론: Linear Classification
결국 Linear Classification은 단순히 행렬과 벡터의 곱 의 형태라는 것을 알았고, 템플릿 매칭 과 관련이 있습니다.
이러한 관점에서 각 카테고리에 대해 하나의 템플릿을 학습 한다는 것도 배웠습니다.
그리고 가중치 행렬 W를 학습시키고 나면 새로운 학습 데이터에도 스코어를 매길 수 있습니다.
이러한 관점에서 Train 시간 은 O(N) 만큼 필요하지만 Test 시간 은 O(1)으로 우리가 원하던 Test 시간을 가집니다.