딥러닝 6일차

오늘은 어제에 이어서
6장의 내용을 볼 것이다.

6.1.1 인공 신경망

뉴런의 동작 구조 같은 것을 배웠다.

뉴런의 입력이 어떻게 계산되어서 출력이 어떻게 되는지에 대한 줄기에 대해서 배워다.

가중합을 구하고 그것을 활성화 함수를 이용하여 출력을 구한다.
활성화 함수를 통해 값들이 달라지낟.

출력은 0,1 또는 음수, 또는 자유로운 수가 나올 수 있다.

입력은 여러개 바이어스(편향 값)이 있다.

편향은 아무런 입력이 없어도 뉴런 자체에 입력이 기본으로 되는 특성값이라고 보면 된다.

계산을 위해서 바이어스를 입력이 항상 1인 거기에 가중치를 곱한것이 바이어스

시그마를 이용해서 간단히 표현이 된다.

원래의 의미는 단순한 선형식이다.

곱해서 더하고 곱해서 더하는 그런 식

신경망 모델에 수학 적 방식은 아래와 같다.

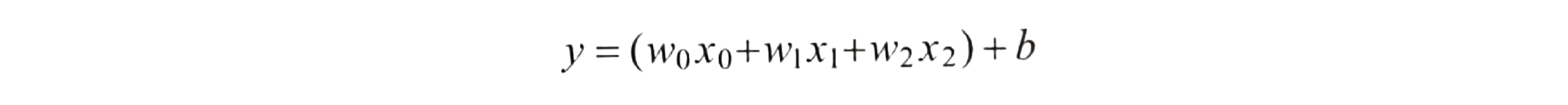
가중치와 편향값에 따라 결과값이 다르게 나온다 -> 이것을 조정함으로서 실제값과 출력값과의 차이를 줄일 수 있다.

학습

• 실제 정답에 근사하는 출력값을 만드리 위해 뉴런의 가중치와 편향값을 반복적으로 조정하는 과정

활성화 함수

• 신경망 뉴런에서 입력된 신호가 특정 강도 이상일 때만 다음 뉴런으로 신호를 보내는 역할
• 가중치 합을 입력으로 받음

대표적인 활성화 함수 3가지

• 계단 함수
• 시그모이드 함수
• 렐루 함수

스텝 함수
입력값이 양수일 때만 1로 바꾼다.

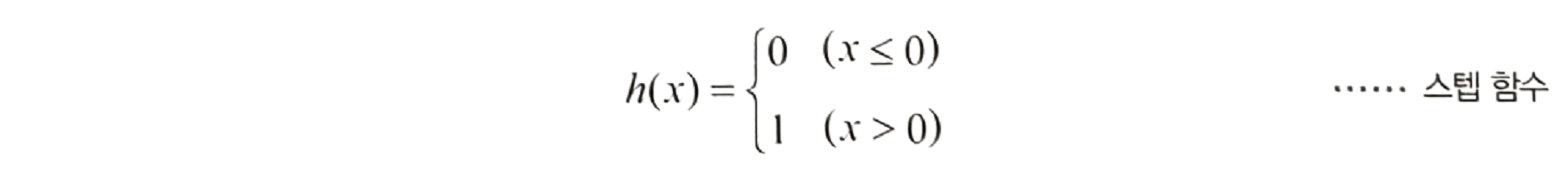
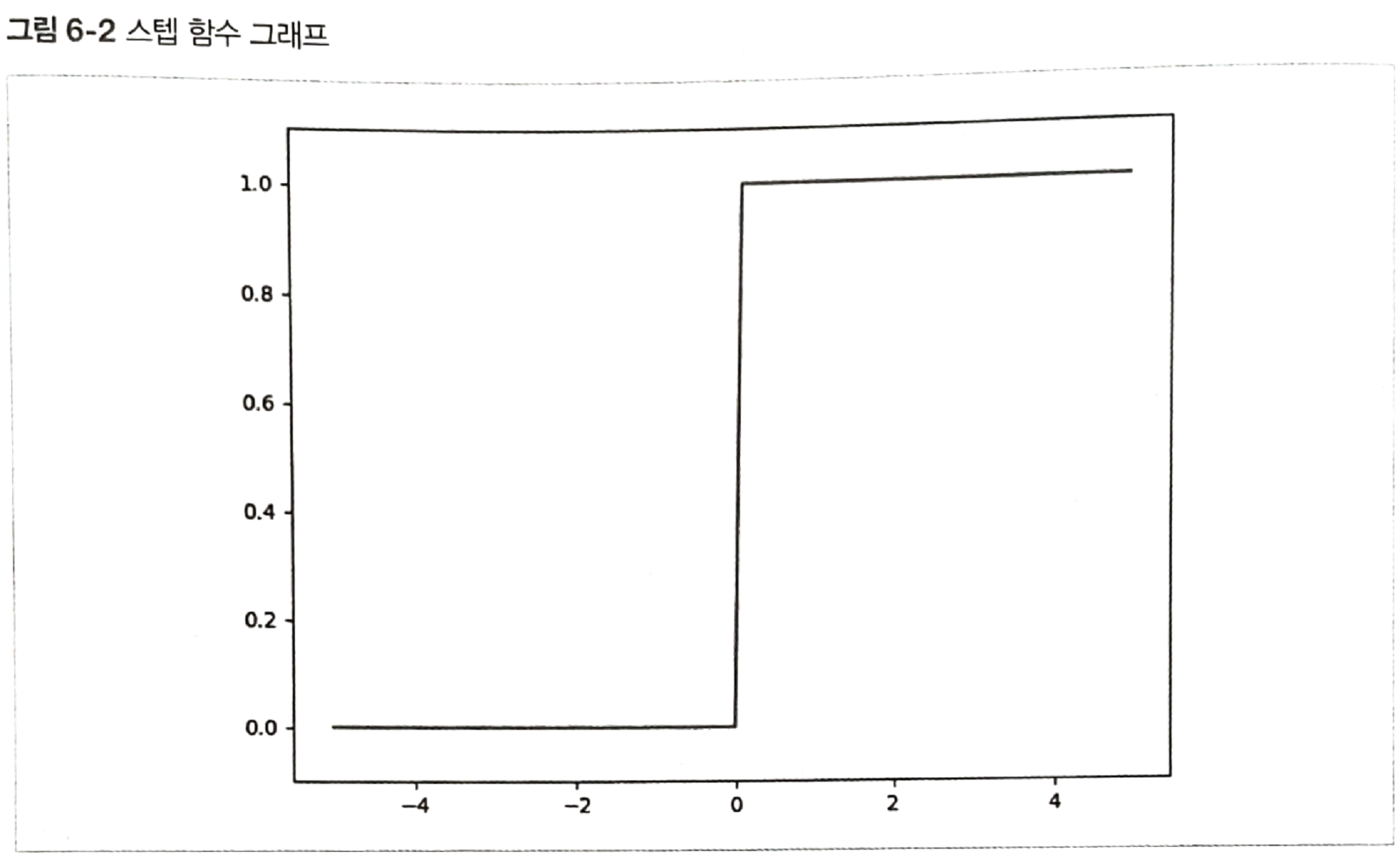
• 활용 : 합격/불합격, Y/N, True/False, Spam/Ham 등 이진 분류 문제
• 단점 : 0을 기준으로 값이 급격하게 변함
  확률 표현에 부접합
  0에서 미분 불가능 -> 역전파 불가

역전파 불가는 결국 학습과정이 힘들어진다.

깊은 신경망에서는 사용이 가능하지만 언제 폭주할 지 모르기 때문에 사용하지 않는다.

시그모이드 함수

• 임계지점에서 미분 가능
• 출력이 [0..1] 확률로 표현
• 합격/불합격일 확률, Y/N 확률, 참/거짓일 확률, 스팸/햄 메일 확률
• 단점 :
  - 입력값이 아주 작거나 커질수록 미분값이 0으로 수렴
  - 딥러닝 시(신경망이 깊을 수록) 학습이 안됨
  - Gradient Vannishing Problem
  - exp()로 인한 계산 비용 상승
  

로지스틱 함수 : 개체군의 성장 등을 나타내는 함수

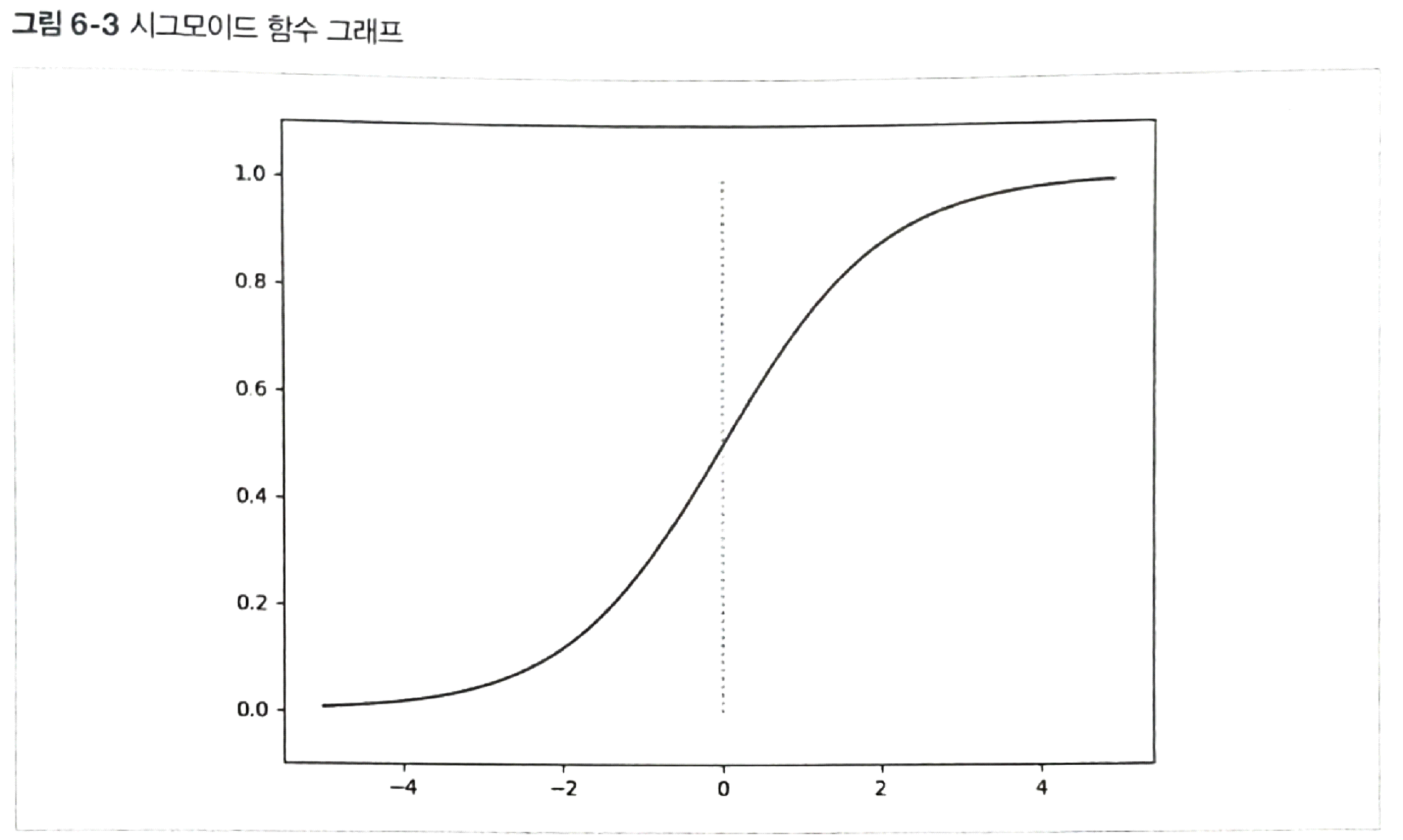
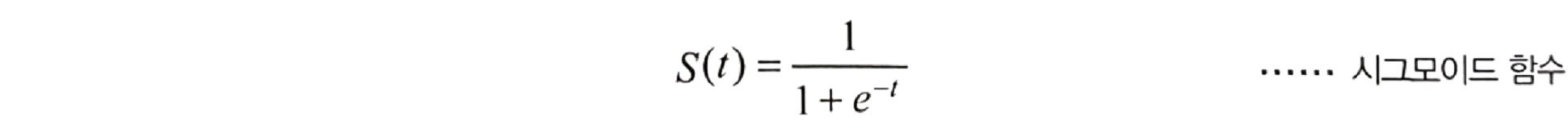
t가 입력이다.
t값이 무한대로 가면 1/1이 된다.
t값이 - 무한대로 가면 0.0아 된다.

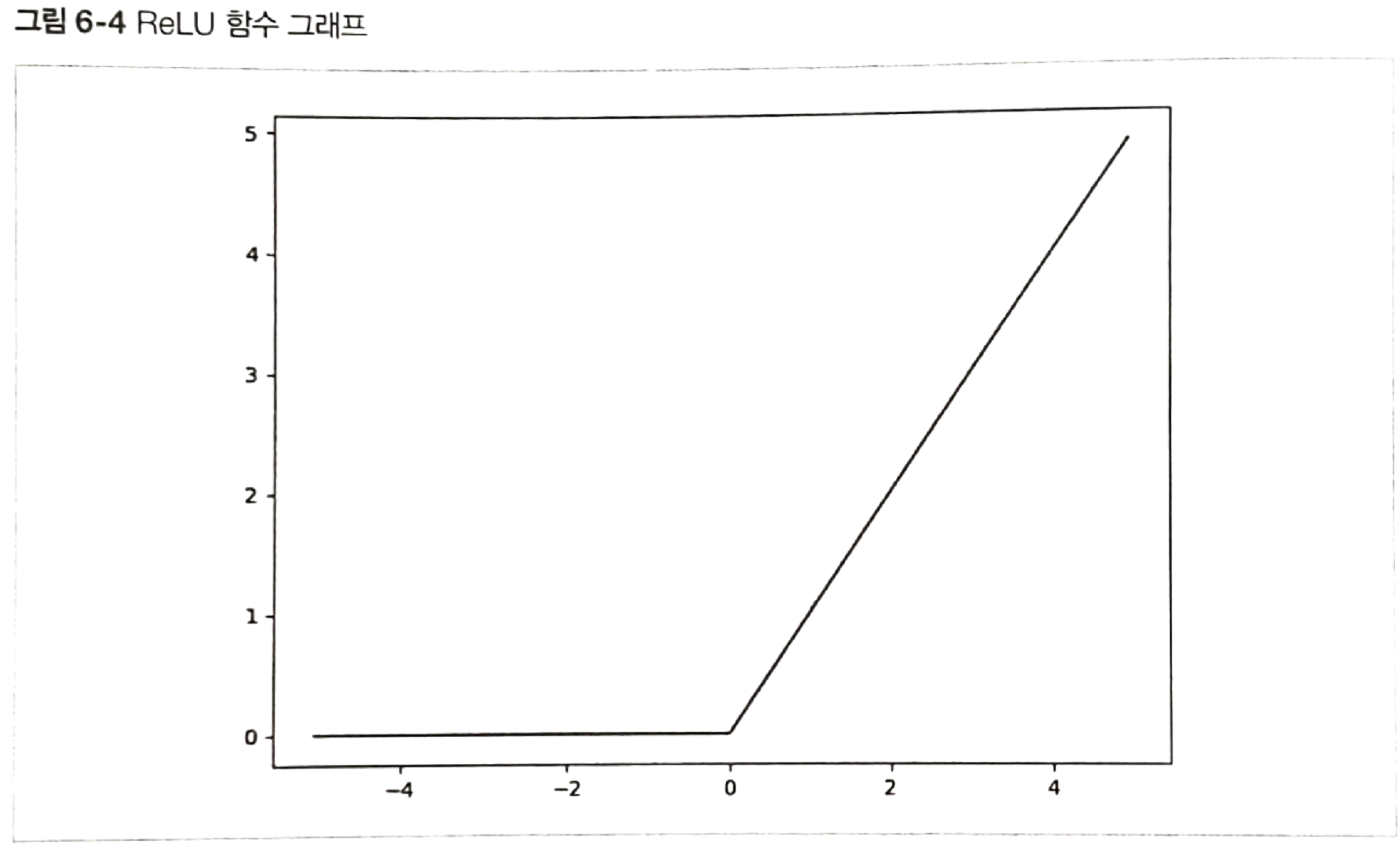
렐루 함수

• 저비용 연산
• 일반적으로 출력값은 양수인 경우가 많으므로 미분값이 0으로 수렴하는 경우가 낮음
• 즉, Gradient Vanishing 문제가 해결됨 -> 딥러닝에 사용

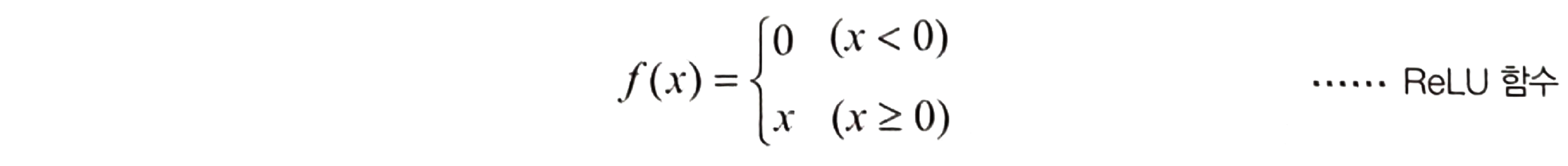
입력층, 은닉층, 출력층

• Layer : 노드(뉴런)들로 구성
• 은닉층 개수, 층별 노드 개수는 파이퍼파라미터, 실험을 통해 최적의 개수를 결정

모델을 학습시키기 전에 우리가 결정하는 값이다.

그러면 어떤 것이 최적의 값인가? 실험을 통해 정해준다.

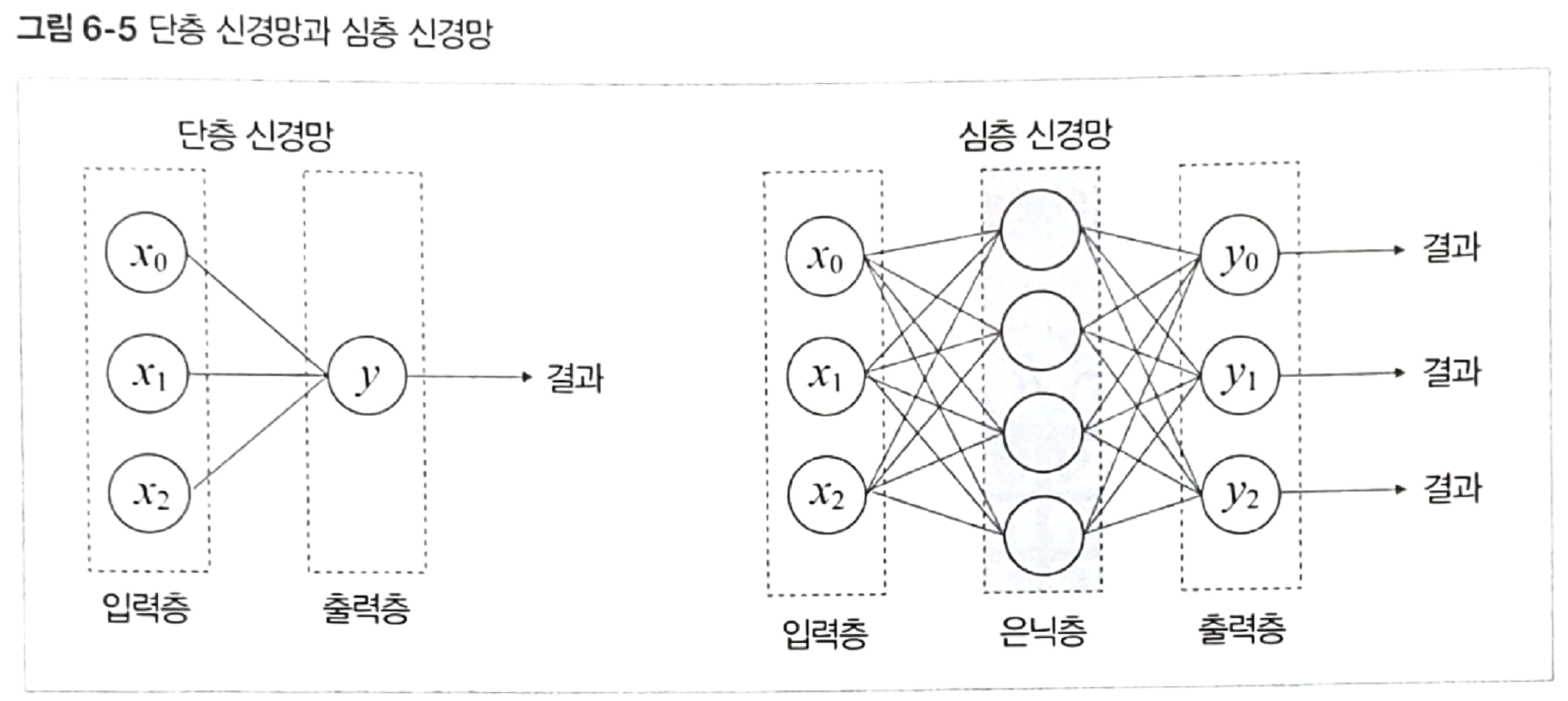
단층 신견망과 심층 신경망
입력층은 말로는 층이지만 노드는 아니라고 본다/ 하지만 일반적인 경우에는 노드라고 표시할 뿐

2진 분류 문제면 계단 함수나 시그모드 함수나 하이퍼 몰리 함수를 사용한다.

다중 분류 문제면 노드를 여러개로 늘리고 시그몰드를 사용하여 확률을 표현한다.

실수라면 y의 활성화 함수는 y=x 같은 입력한 값을 그대로 내보낸다.

층이 2개이지만 웨이트를 합한 것 하나가 나온다.

심층 신경망의 경우 웨이트 집합이 있고 은닉층과 출력층에서도 가중치가 있어서 여러번의 가중치 계산이 발생한다.

신경망의 학습 과정(간단 설명)

• 순전파 후
• 오차 기반의 손실 계산 후
• 역전파로 오차를 줄이는 방향으로 가중치 조정

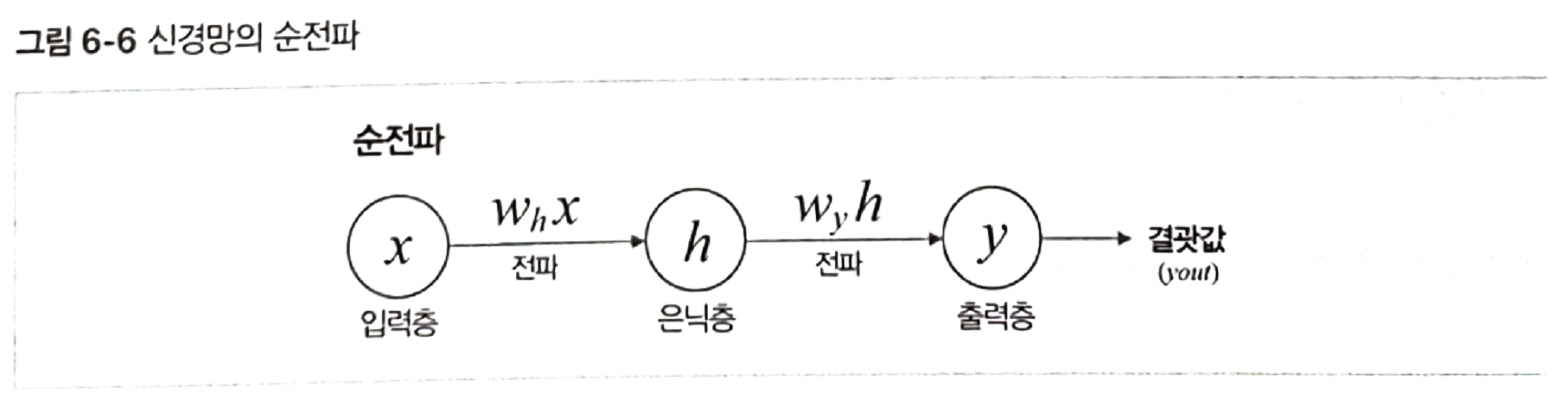
순전파 : 신경망 모델에서 입력층으로부터 출력층까지 데이터가 순방향으로 전파되는 과정을 순전파라 합니다.

데이터가 순방향으로 전파될 때 (현 단계 뉴런의 가중치와 전 단계 뉴런의 출력값의 곱)을 입력값으로 받습니다.
이 값을 다시 활성화 함수를 통해 다음 뉴런으로 전파됩니다. 최종적으로 출력층에서 나온 결과값(yout)이 모델에서 예상한 값

이미 학습이 완료되어 최적의 가중치를 찾았다면 해당 결과값은 모델의 예측값으로 활용할 수 있습니다.
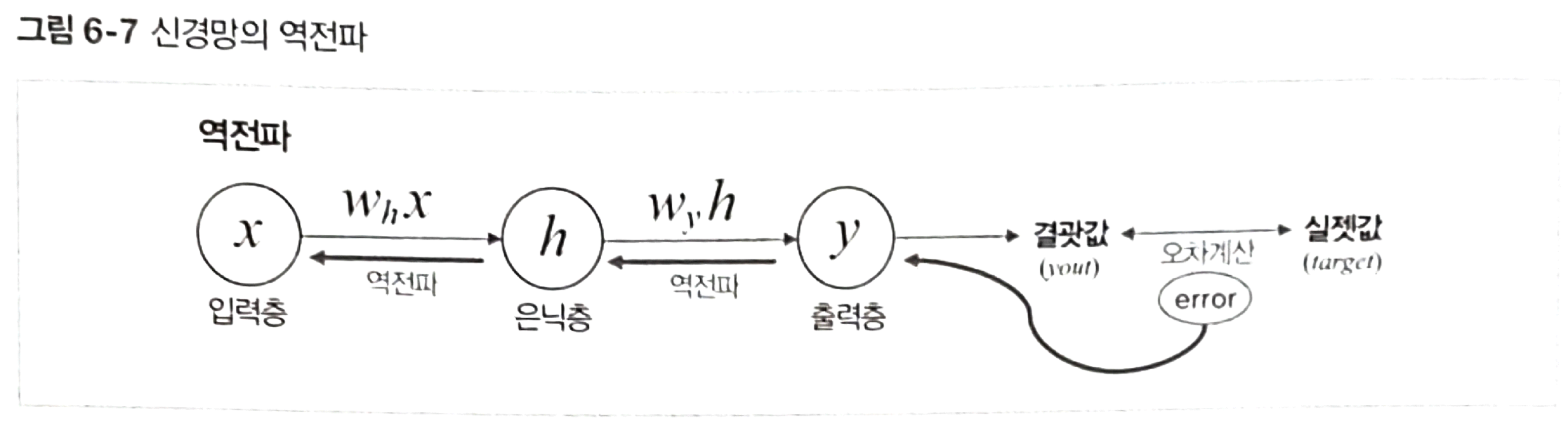
하지만 우리가 목표하는 실젯값과 비교해 오차가 많이 발생했다면 다음 순전파 진행 시 오차가 줄어드는 방향으로 가중치를 역방향으로 갱신해나갑니다. 이 과정을 역전파라고 합니다.

다른 머신러닝들 또한 이렇게 한다.

모델 파라미터의 함수로 만들면 모델 파리미터로 미분할 수 있고 손실을 최소화하는 방향으로 할 수 있다.

신경망의 차이는 층으로 구성되어 있어서 출력층에 가중치를 업데이트한다.

순전파 할때 순전파가 다 끝나면 오차를 구할 수 있지만 역전파시 은닉층에서 나오는 값은 결과값이다.

현재 스텝에서 은닉층에 실제 값이 무엇이 되어여할지 계산할 수 있다.

은닉층에 오차를 구하게 되면 가중치를 업데이트 할 수 있다.

시그몰드를 사용하면 처음은 되는데 뒤로 뒤로 갈수록 가중치가 아주 크거나 작아진다.
좌우로 치우치게 된다.
층이 깊어질수록 미분이 0으로 되면서 학습이 잘 되지 않는데
렐루 함수를 사용하면 이를 어느 정도 극복할 수 있다.

https://github.com/keiraydev/chatbot
코드 다운로드

tensorflow 설치

설치 버전 확인 pip list

tensor 가 앞에 있는 패지키들만 찾기

설치된 패키지 개수 세기

응용

unix 철학
하나의 기능은 최소한의 기능만을 구현

가상환경에 CUDA 깔기

NVIDIA가 있으니까 그것을 사용하여 한다.

NUMPY

주요 객체는 Basisc

튜플은 논 네거티브

넘파이 차원을 축이라고 한다.

3차원 공간에 어떠한 점을 [1,2,1]이라고 표현을 하지만 대괄호가 1개이니까 축이 1개이다.

numpy의 차원 수는 축의 수와 같다.

축은 한개이다. 이 점을 3차원의 점으로 정의
원소의 개수는 축의 길이다.

아래에 그림을 보면
[[1,0,0],
[0,1,2]]
2개의 축을 가지고 있다.

가로로 가는 축은 원소가 3개
엑시스와 엑시즈

numpy.array

https://numpy.org/doc/stable/user/quickstart.html

여기 내용을 정리할 것