MATLAB 예제풀기 1

1) 1,000부터 1,000,000의 범위 내에서 5개의 값을 갖는 벡터 'W'를 logspace를 사용하여 생성하기

W = logspace(3,6,5)

W =

1.0e+06 *

0.0010    0.0056    0.0316    0.1778    1.0000
  

2) 다음과 같은 벡터'a'에 대한 exp,log,sqrt,floor 연산 결과 적기

a=[-0.3 0.5 0.2 0.4 0.7]
exp(a),log(a),sqrt(a),floor(a)

ans =

0.7408 1.6487 1.2214 1.4918 2.0138

• epx(a)는 자연상수e의 지수값에 대입한 것을 말함.

ans =

-1.2040 + 3.1416i -0.6931 + 0.0000i -1.6094 + 0.0000i -0.9163 + 0.0000i -0.3567 + 0.0000i

• log(a)는 로그의 밑이 자연상수인e인 것에 대입하는 결과들을 출력함.

ans =

0.0000 + 0.5477i 0.7071 + 0.0000i 0.4472 + 0.0000i 0.6325 + 0.0000i 0.8367 + 0.0000i

• sqrt(a)는 거듭제곱을 의미한다.

ans =

-1 0 0 0 0

• floor(a)는 버림이다.

3) 2행 5열의 벡터 'W'를 다음의 조건에 맞게 생성하시오.

• 1행 : 0부터 5까지 5개(linspace 사용)
• 2행 : 0부터 8까지 2의 간격(콜론 연산자 사용)

W=linspace(0,5,5)
W=0:2:8

4) a=[8.7, 3.8, 2.5, 5.7, 1.9] 벡터의 평균, 분산, 표준편차를 구하시오.
(단 출력은 소수점 세째 자리에서 반올림 하여라)

반올림 할 때 round를 사용하면 되는데 자릿수도 정할 수 있다.

이런식으로 작성하여 round(,2)를 해서 둘째자리까지 반올림 하게 하여 결과를 나타내면 된다.

5) a=[1,2,3], b=[2,5,6]일때 a와 b의 내적과 a의 전치와 b의 곱을 적으시오

dot(a,b), a'*b

ans =

30

ans =

 2     5     6
 4    10    12
 6    15    18

6) d=[1,2,3,4,5;6,7,8,9,0]의 행렬을 1행 10열로 표현하시오.(단 수식은 한줄로 표현해야 된다.)

d=[1,2,3,4,5;6,7,8,9,0] 여기서
d=[1,2,3,4,5,6,7,8,9,0]이걸로 바꾼다.
;(세미콜론의 차이로 1행 10열이 아닌 2행 5열로 만들어진 경우)

7) d=[1,2,3,4,5;6,7,8,9,0]의 행렬을 10행 1열과 1행 10열로 만든 행렬들의 곱을 출력하시오.
(단 수식은 한줄로 표현 해야 된다.)

d=[1,2,3,4,5;6,7,8,9,0]을
d', d=[1,2,3,4,5,6,7,8,9,0]으로 출력한다.

8) a=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20]가 주어졌을 경우 1행 3열부터 5열까지와 3, 4행 3열부터 5열까지의 원소를 추출하여 3행 3열의 행렬을 만드시오.
(단 수식은 한줄로 표현 해야 된다.)
ex) a=[3,4,5;13,14,15;18,19,20]

a=[a(1,3:5); a(3:4,3:5)]

a(1,3:5)는 1행, 3열부터 5열과 ;(세미콜론)하고 a(3:4,3:5)는 3행부터 4행까지 3열부터 5열 출력을 의미한다.

 3     4     5
13    14    15
18    19    20

또는

a([1,3:4],[3:5])

이 경우는 [행],[열] 이런식으로 이루어져 있다. 첫번째는 가져올 행들을 선택하는 것이고, 두번째는 가져올 열들을 선택하는 것이다. 개인적으로 이 방법이 더 좋은 것 같다.

 3     4     5
13    14    15
18    19    20

9) 0~1사이의 uniform 분포를 가지는 5x5 행렬 A를 생성하시오.

rand(5)

10) 어떠한 행렬 A가 주어졌을 때 A^2 와 A.^2의 차이점을 서술하여라
앞 시간에 나온 것 처럼 a^2는 행렬의 제곱이면 a.^2는 요소의 곱이다.

a^2

ans =

 7    10
15    22

a.^2

ans =

 1     4
 9    16

k=sqrt(5)

k =

2.2361

8+((6*(1+k))/2)

ans =

17.7082

---

4/3 x pi x 10^3

ans =

4.1888e+03

---

exp(sqrt(3))+pi*10^3

ans =

3.1472e+03

---

q=pi*sqrt(-1)

q =

0.0000 + 3.1416i

exp(q)

ans =

-1.0000 + 0.0000i

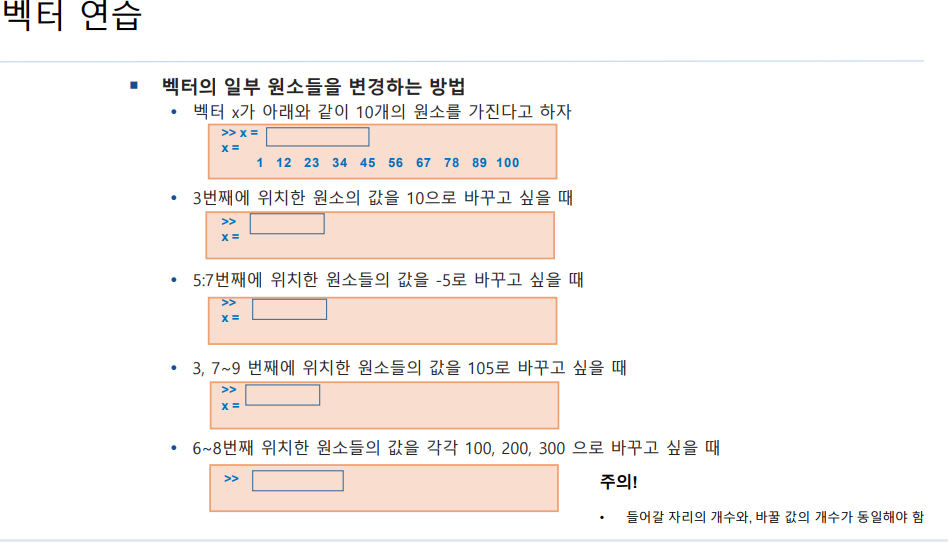
x(3:6)
x(1),x(5),x(7) or x=[x(1),x(5),x(7)](이건 한번에 출력)
x(3),x(7:9) or x= [x(3),x(7:9)]

x=linspace(1,100,10)

x =

 1    12    23    34    45    56    67    78    89   100

x([3])=10

x =

 1    12    10    34    45    56    67    78    89   100

x([5:7])=-5

x =

 1    12    10    34    -5    -5    -5    78    89   100

x([3,7:9])=105

x =

 1    12   105    34    -5    -5   105   105   105   100

x([6:8])=linspace(100,300,3)

x =

 1    12   105    34    -5   100   200   300   105   100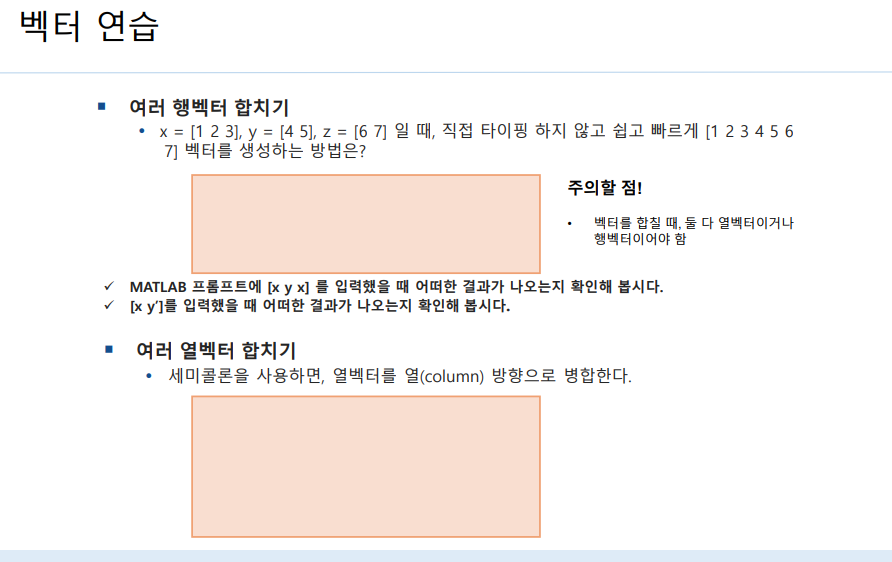

x=[x,y,z]
x=[x,y,x]는 1 2 3 4 5 1 2 3 이 나온다.