[CVPR 2020] Orthogonal Convolutional Neural Networks

introduction

CNN의 압도적인 성공에도 불구하고, 여전히 몇가지 약점이 존재한다: overparametrization, gradient exploding/vanishing, etc...

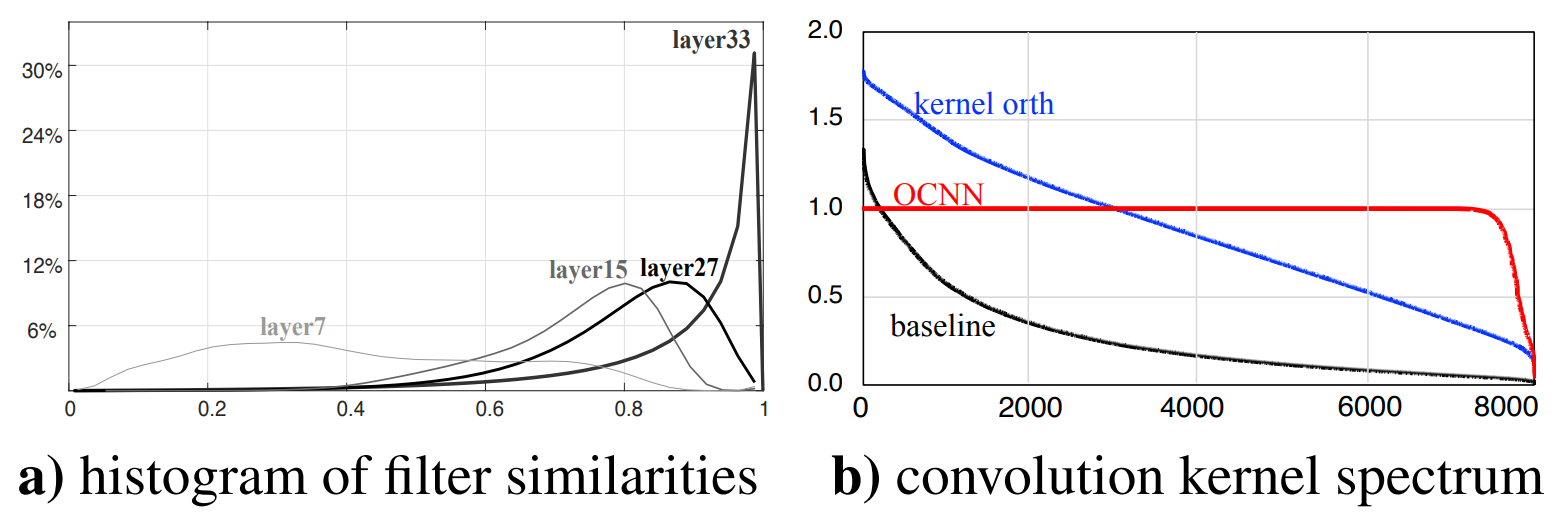
저자들은 이러한 약점의 원인이 convoltional filter간의 high correlation과 long-tailed spectrum에 의해 일어난다고 주장한다.

위의 그래프는 각각 layer의 깊이 별 filter similarity histogram과 kernel spectrum을 plot한것으로, 레이어가 깊어질수록 각 convolutioal kernel들이 비슷한 방향으로 수렴하여 redundant한 parameter들이 늘어나는것을 볼 수 있다.
또한 spectrum의 불균일한 분포는 convolution 연산 이후의 activation에 대한 scale을 일정하게 유지하지 못하게 만들고, 이는 결국 gradient의 불안정함으로 이어진다고 주장한다.

기존의 연구에서는 이러한 filter끼리의 similarity를 낮추고 spectrum을 일정하게 유지하기 위해 orthogonality regularization을 주었다.
하지만 이 논문에서는 기존 연구에서 regulrization을 정의하기 위해 convolution 연산을 matrix-matrix multiplication의 문제로 formulation하는 과정에서 불충분한 점이 있었음을 지적하며, 자신들의 새로운 formulation 방법이 기존의 방법을 커버하는 더 근본적인 방법임을 주장한다.

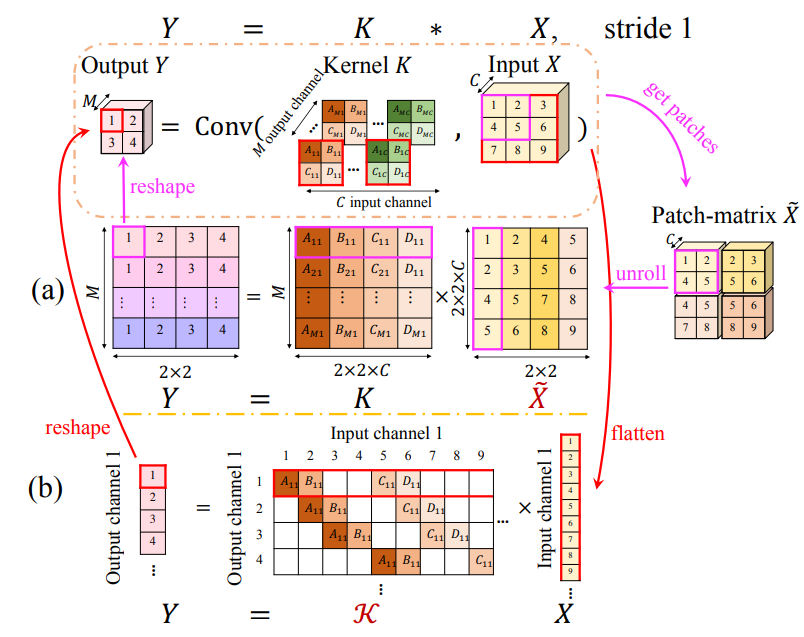
kernel orthogonality

기존의 연구에서는 convolutional operation을 각 patch가 column vector에 대응되는 im2col matrix $\tilde X$에 kernel matrix $K$ 가 행렬곱된

꼴로 해석하여, kernel matrix에 orthogonality regularization (i.e. $||K^TK-I||$)를 주었다.
하지만 이 formulation은 $X$와 $Y$간의 direct relation을 제시해주지 않고 $\tilde X$를 사용하기 때문에, $K$의 orthogonality가 uniform spectrum을 보장해주지 않는다.

orthogonal convolution

이 논문에서는 convolutional operation을 Kernel matrix를 변형하여

꼴의 representation을 가질 수 있는 Doubly block-toeplitz (DBT) matrix $\mathcal{K}$를 정의한 뒤, $\mathcal{K}$에 대해 orthogonality regularization을 주었다.

또한 $||\mathcal{K}^T\mathcal{K}-I||$를 계산하는 과정이 infeasible함을 지적하면서, 대신에 $||Conv(\mathcal{K},\mathcal{K}) - I||$를 regularizer로 사용하는 것으로 $\mathcal{K}$의 orthogonality를 얻을 수 있음을 보였다.

Orthogonal Convolution

먼저, orthogonal convolution을 정의하기에 앞서 convolution을 matrix multiplication으로 정의하는 방법부터 살펴보자.

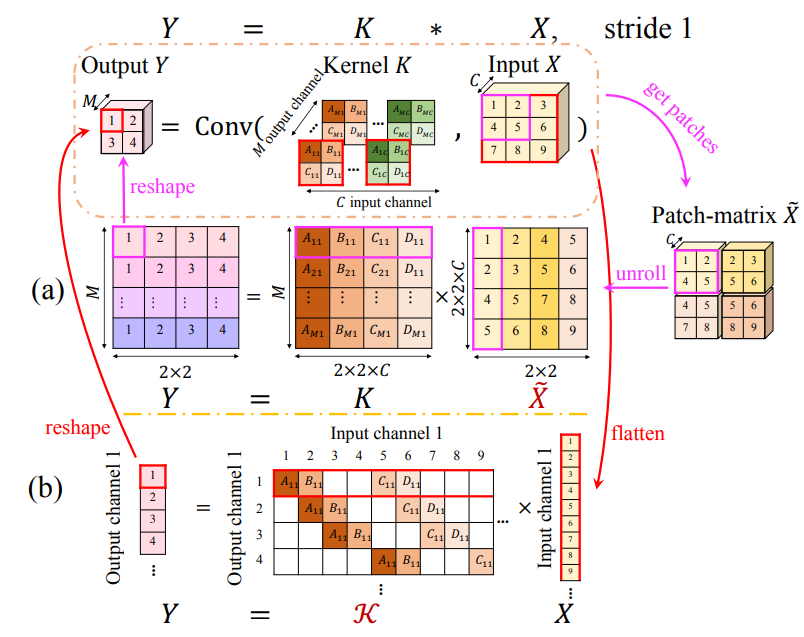
(이미지 재탕 죄송..) 간단하게 3x3 image에 2x2, stride 1 kernel을 적용하는 2d convolution의 예시를 생각해보면, flatten된 9 dimensional vextor $\bold x$의 $(1,2,4,5),(2,3,5,6),(4,5,7,8),(5,6,8,9)$번째 component와 kernel의 $(1,2,3,4)$번째 component를 곱하는 것으로 생각할 수 있다.
이를 matrix로 나타내면 $\bold x$에 $4 \times 9$ doubly block-toeplitz matrix $\mathcal{K}$를 곱한 것으로 이해할 수 있다.

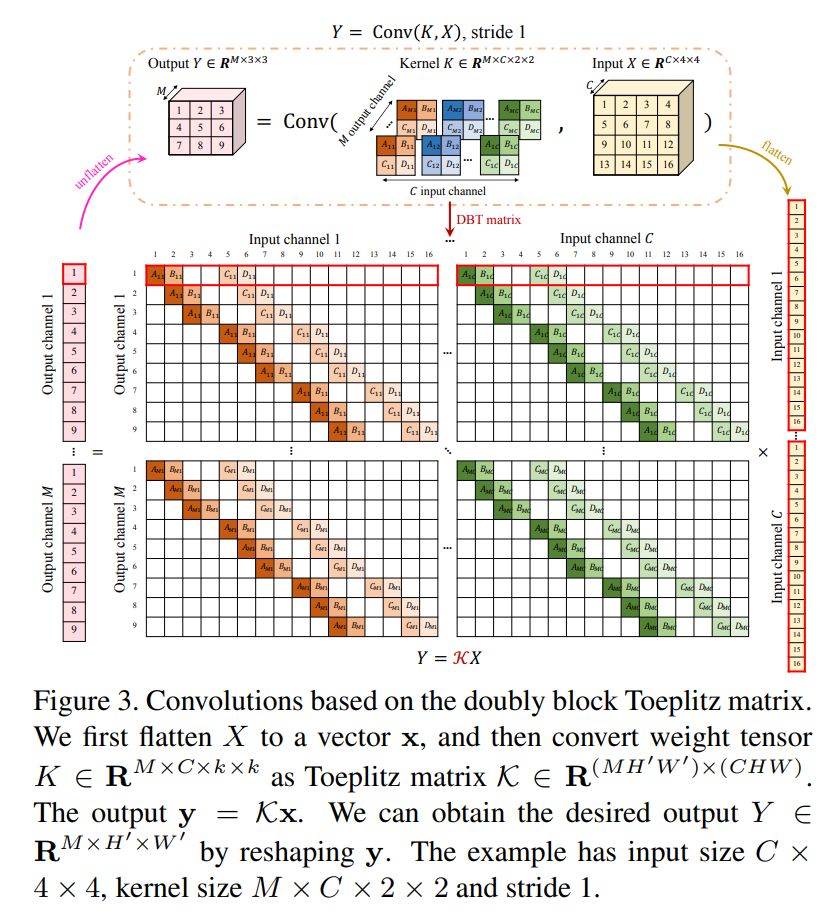
이제 Input tensor $X\in R^{C\times H\times W}$에 M개의 kernel $K\in R^{M\times C\times k\times k}$를 사용하여 convolutional operation $Y = Conv(K,X) \in R^{C\times H'\times W'}$를 행한다고 생각해보자.
이 때 $X$를 flatten한 vector $\bold x$에 대해 각 block이 $C$번째 channel에 대한 $M$번째 kernel의 convolution으로 작용하는 $\mathcal{K}\in R^{(MH'W') \times (CHW)}$를 생각하면,

의 꼴로 연산을 나타낼 수 있다.

Convolutional Orthogonality

간단하게 $(MH'W')<(CHW)$인 케이스에 대해 먼저 생각해보자.

$\mathcal{K}\in R^{(MH'W') \times (CHW)}$가 orthogonal하다는 것은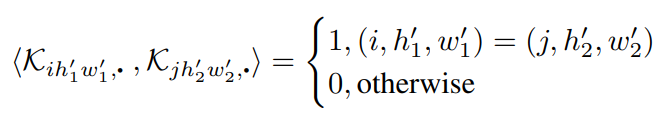
을 만족한다는 것이고, 이 때
$\langle \mathcal{K}_{ih_1'w_1'},\mathcal{K}_{ih_2'w_2'} \rangle \not = 0$ iff $|h_1-h_2|<k$ and $|w_1-w_2|<k$
이므로,
$||\mathcal{K}^T\mathcal{K} - I|| = 0$ iff $||Conv(\mathcal{K},\mathcal{K}) - I|| = 0$
이 된다.
또한 $(MH'W')>(CHW)$인 케이스에 대해서는
두 조건이 MSE sense에 대해 동일하므로 위의 regularizer를 사용하는게 문제가 없다.

마지막으로 kernel orthogonality에 대해서

위의 조건을 만족하여야 하는데, 이는 orthogonal convolution의 필요조건중 하나이므로, 이 regularization이 기존의 방법을 포함하는 방법임을 보여준다.

Result

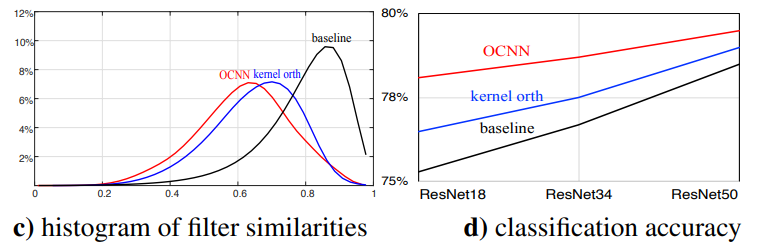
Similarity도 낮추고 성능도 올라갔다고 합니다.
와~