[2015 ICML] Deep Unsupervised Learning using Nonequilibrium Thermodynamics

1. introduction

머신러닝의 주요한 과제 중 하나는 복잡한 데이터셋을 flexible한 probalistic model을 통해 모델링 하는 것이다.
probalistic model은 두 가지에 목적에 대해 trade-off를 갖는다: tractability, flexibility.
tractability는 간단히 얘기해서 해석적으로 계산이 잘 되고 데이터에 쉽게 fit할 수 있는 성질을 뜻한다. 가장 널리 쓰이는 Gaussian distribution 등이 이러한 예에 속한다.
하지만 이러한 모델의 경우 복잡한 데이터셋을 표현할 정도의 풍부한 표현력이 부족한 경우가 많다.
반면 flexibility의 경우 임의의 데이터에 대해 fit할 수 있는 능력을 뜻하는 것으로, set of any non-negative function을 생각해보면 어떤 데이터셋에도 fit할 수 있는 함수

를 찾을 수 있겠지만, normalizing constant Z를 계산하는 것은 일반적으로 불가능한 경우가 많다. 이러한 flexible한 모델에 대해 eval/train/sampling을 하기 위해서는 매우 무거운 Monte Carlo Simulation을 행해야 할 때가 많다.

이 논문에서는 다음과 같은 장점을 가진 Diffusion Probalistic Model을 제안한다.
1. extreme flexibility in model structure,
2. exact sampling,
3. easy multiplication with other distributions, e.g. in order to compute a posterior, and
4. the model log likelihood, and the probability of individual states, to be cheaply evaluated.

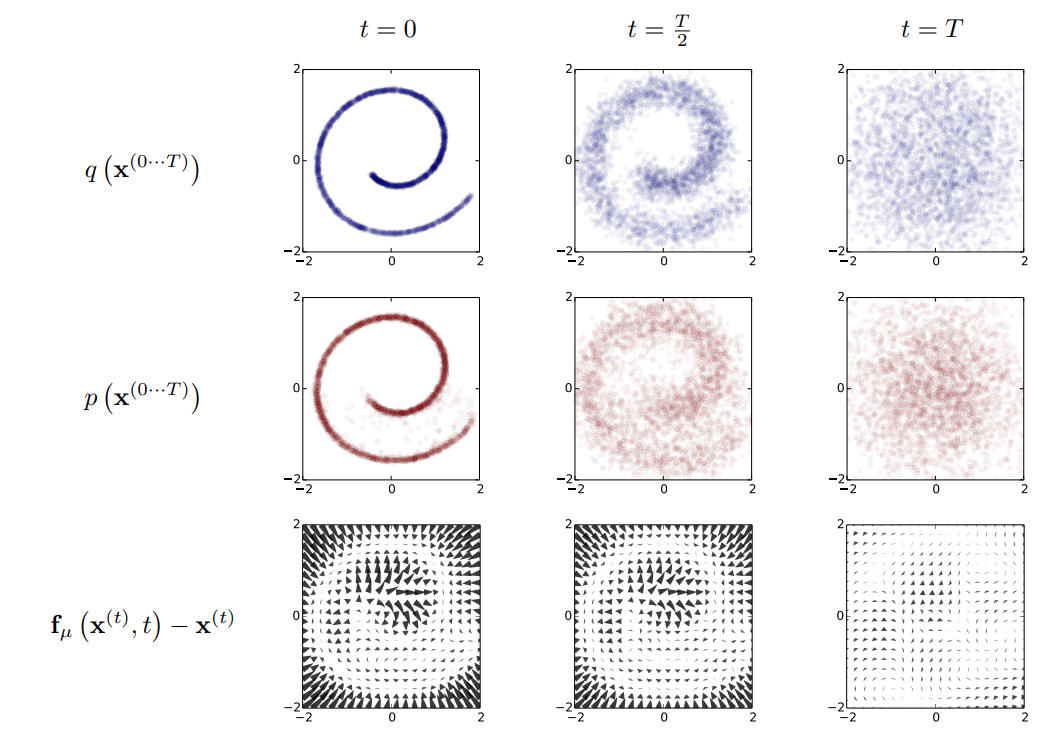
Diffusion model의 목표는 complex data distribution과 simple distribution (e.g. Gaussian)간의 transformation/inverse transformation을 학습하여 data distribution을 간단한 분포로 모델링하는 것이다.

Diffusion model은 확산 방정식을 활용하여 복잡한 데이터 분포를 간단하고 알려진 분포 (e.g. Gaussian)로 변환하는 diffusion process를 진행한다.

그 다음 Gaussian 분포에서 데이터 분포를 복원하는 backward process를 다시 확산 방정식을 통해 정의하고, 기존의 데이터와 복원 후 데이터간의 log-likelihood를 최대화하는 방향으로 파라미터를 학습한다.

이러한 확산 방정식을 구현하는 것은 시간을 t=0,1,...,T로 discretize한 후 각 time step t에서의 값이 t-1에서의 값에만 의존하는 Markov transition kernel을 데이터에 적용하는 것으로, 학습 과정에서는 forward process의 각 time step에서의 diffusion rate $\beta_t$ 와 backward process의 각 time step에서의 kernel parameter (e.g. $(f_{\mu}(x^{(t)},t),f_{\Sigma}(x^{(t)},t))$ for Gaussian)만을 학습한다.

이러한 kernel parameter function을 regression하는 함수는 여러 가지가 있겠지만, 이 논문에서는 multi-layer perceptron을 사용하였다고 한다.

Relationship to other work

이 논문은 머신러닝 방면으로는 wake-sleep algorithm (Hinton, 1995)에 기초하고 있으며, 이는 input data를 latent vector로 encode 하는 wake phase와 이 vector를 data sample로 decote하는 sleep phase로 이뤄진 알고리즘이다.
현대적인 딥러닝에서는 VAE (Variational Autoencoder)가 대표적으로, intractible distribution을 simple distribution으로 변환하여 다루는데 효과적인 알고리즘이다.

또한 물리학 방면으로는 Kolmogorov forward/backward equation과 Annealed Importance Sampling (AIS)로 machine learning 분야에서 잘 알려진 Jarzynski equality의 아이디어를 사용한다.

Kolmogorov forward/backward equation은 기체의 확산과 그의 역 과정을 수식으로 나타낸 것으로, 특정한 drag force와 random force 하에서 입자들의 probability density function이 시간에 따라 어떻게 진화하는 지를 나타내는 등식이다.

forward equation은 Fokker-Planck equation으로도 알려져있으며, Langevin dynamics를 통해 각 입자의 운동에 대한 stochastic realization을 구현할 수 있다.

이 때 potential function을 조절하여 equilibrium distribution을 원하는 target distribution으로 수렴하게 할 수 있다. (e.g. $\; V(x) = \frac{k}{2}(x-\mu)^2$ for Gaussian)

backward equation은 forward process의 time reversal의 계산을 feasible하게 해주는 등식으로, 이에 대한 Langevin dynamics를 구하기 위해서는 확률 분포의 시간에 따른 gradient를 알아야 한다.

AIS는 복잡한 target distribution의 nomalizing constant를 계산하기 위해 고안된 방법으로, simple initial distribution으로부터 시작해서 target distribution에 가까워지도록 intermediate distribution을 만들어 (i.e. MCMC transition) sampling을 하는 방법이다.
또한 (Burda et al., 2014)에 의하면 reverse transition operator를 계산함으로써 target distribution으로부터 initial distribution을 sampling하는 역방향 AIS도 행할 수 있다고 한다.
이 논문에서는 data distribution과 target distribution간의 transition 과정을 AIS에서의 intermediate distribution의 관점으로 해석하여 marginal distribution의 계산을 훨씬 tractible하게 해주었다.

2. Algorithm

forward process

Forward process의 목적은 복잡한 data distribution을 simple distribution으로 변환하는 것으로, Gaussian kernel을 사용하여 identity-covariate Gaussian으로 변환하거나/binomial kernel을 이용하여 independant binomial distribution으로 변환하는 두 가지의 방법이 있다.

먼저 initial data를 $\bold x^{(0)}$, 그에 따른 확률 분포를 $q(\bold x^{(0)})$로 나타내도록 하자.
우리의 목표는 $q(\bold x^{(0)})$를 gradual하게 tractible distribution $\pi (y)$로 변환하는 것이다.
이를 연속적인 변수 $y'$에대해 나타내면 다음과 같다.

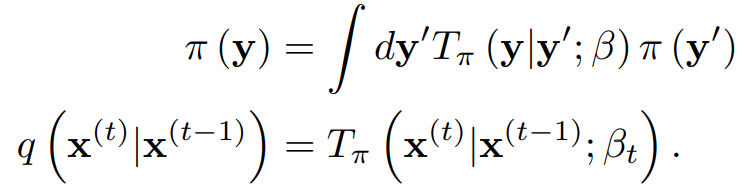
구체적인 kernel의 formulation은 다음과 같다.

(이 kernel이 왜 $\mathcal{N}(0,I)$로 수렴하는지에 대한 증명은 나와있지 않지만, 대략

정도로 이해하면 기댓값은 0, 분산은 $I$로 수렴하는 것이 직관적으로 이해는 간다.)

결론적으로, forward process에서의 joint probability는 다음과 같다.

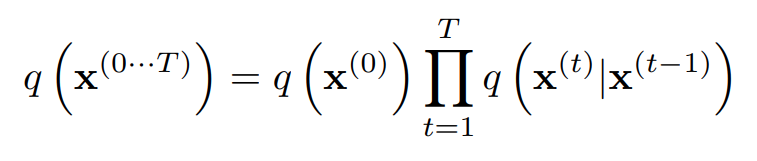
backward process

Backward process는 forward process의 역과정을 계산하는 것으로, forward process와 거의 비슷하게 Gaussian kernel을 적용하는 방식으로 일어난다.

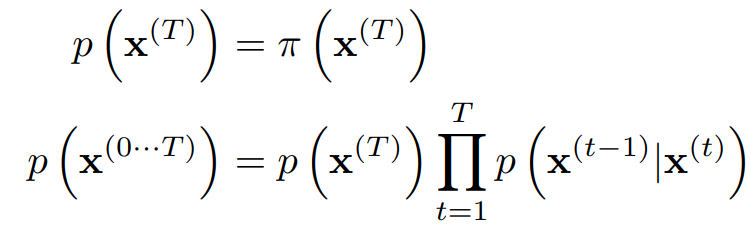
이는 (Feller, 1949)의 Kolmogorov equation에 대한 이론에 기초한 것으로, continuous diffusion with small step size $\beta$의 reversal은 forward process와 identical한 functional form을 가진다고 한다.
따라서 small $\beta_t$에 대해서 $q(x^{(t-1)}|x^{(t)})$ 또한 Gaussian을 따른다고 할 수 있다.

하지만 backward process를 계산하기 위해서는 forward process와 다르게 diffusion rate만 사용하는 것이 아닌 직접적인 mean/variance $(f_{\mu}(x^{(t)},t),f_{\Sigma}(x^{(t)},t))$의 계산이 필요하다.
따라서 이 논문에서는 $f$를 모델링하기 위해 multi-layer perceptron을 사용한 후, 업데이트 하는 방식을 사용하였다.

model probability

Data distribution에 대한 model probability는 다음과 같다.

하지만 margianlization을 직접 하기 위해서는 $T*D_{image}$차원에서의 sampling이 필요하므로 intractible하다.
따라서 이 논문에서는 AIS의 아이디어를 사용하여 relative probability of forward/reverse trajectory를 사용한 값을 구한다.

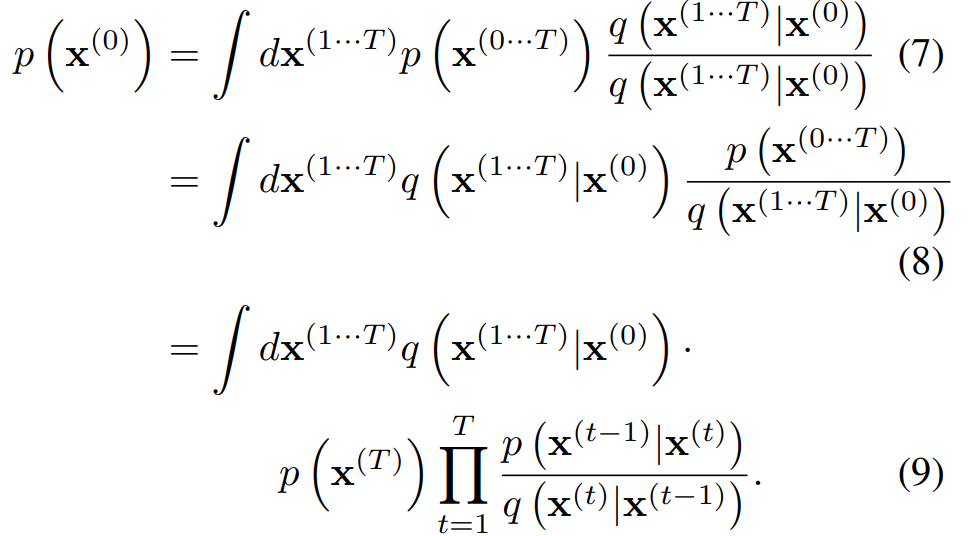
이 적분은 forward trajectory $q(\bold x^{(1... T)}|\bold x^{(0)})$의 sample들에 대해서 transition/reverse transition의 평균을 구하는 것으로 빠르게 행할 수 있다.

논문에서는 이에 더하여 무한히 작은 (infinitesimal) $\beta$에 대하여 forward/backward distribution이 동일하므로, 하나의 sample만을 사용해도 충분하다고 한다. (quasi-static process)

training

Training은 $p(\bold x^{(0)})$과 $q(\bold x^{(0)})$의 log-likelihood를 최대화하는 방향으로 이뤄진다.

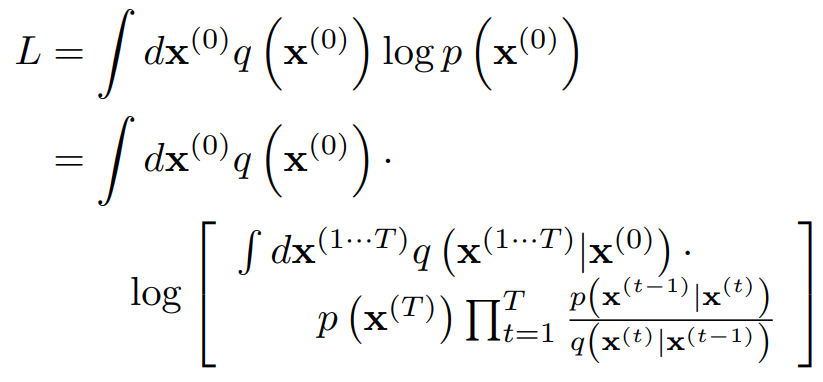
이 때 $log$부분에 옌센 부등식을 적용하면

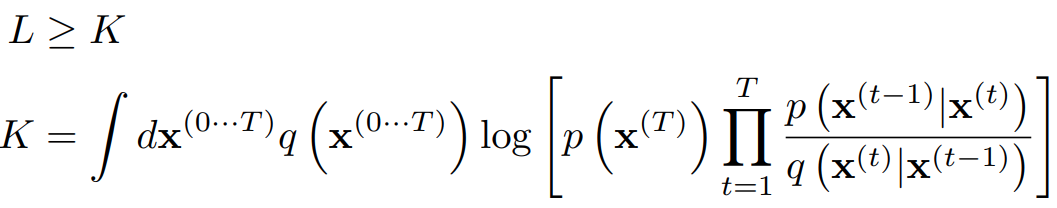
이라는 수식을 얻는다.
우리의 diffusion model에서 얻어진 수식들을 대입하면 다음과 같이 분해할 수 있다.

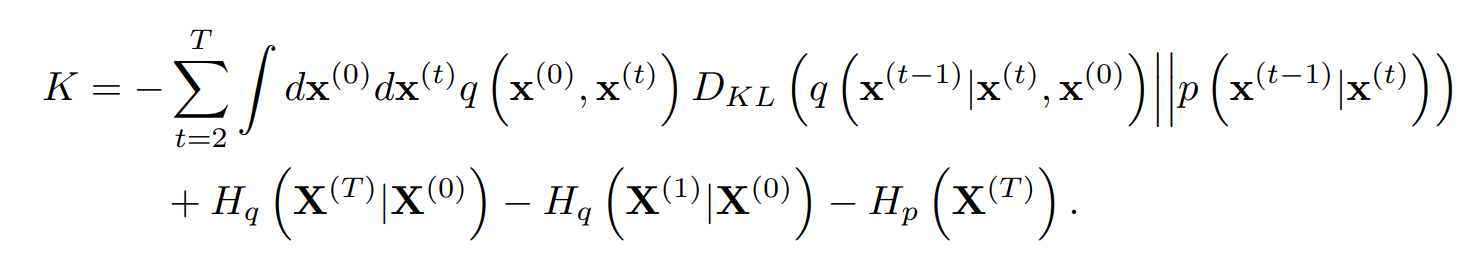
이 때 KLD와 entropy들은 analytic하게 계산 가능하므로, L을 direct하게 최대화하는 대신 Variational Bayesian method에서 ELBO를 최대화 하듯이 lower bound K를 최대화하는 reverse Markov transition을 찾는다.

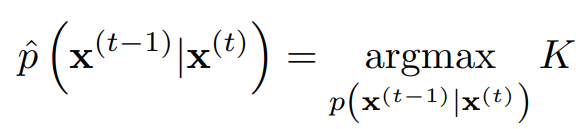
setting the diffusion rate $\beta_t$

해당 논문에서는 $\beta_t$의 선택이 성능에 큰 영향을 미치며, Gaussian의 경우 K에 대해 graident acsent를 행하여 $\beta_t$의 scheduling을 결정한다고 나와있으나 후속 버전에서는 fixed $\beta_t$를 사용하는게 더 효과적이라는 주석이 달려있다.

multiplying distributions, and computing posterior

Posterior을 구하여 denoising과 같은 작업을 하기 위해서는 $p(x^{(0)})$과 second distribution $r(x^{(0)})$간의 곱셈 연산을 해야할 때가 있다.

VAE등의 다른 모델에 있어서 이 과정은 굉장한 computational cost를 요하는 과정이지만, diffusion model에서는 각 diffusion step에 $r(x^{(t)})$를 곱하는 것으로 곱셈을 구현할 수 있다.

이 부분은 수식이 길어지므로 직관적으로 설명하자면,

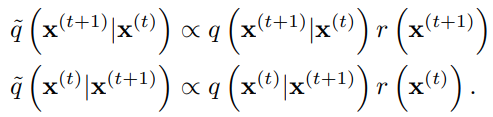
위를 만족하는 Markov Chain을 선택할 수 있다.

이 때 r이 충분히 smooth하면 Gaussian kernel에 perturbation이 가해진 형태의 diffusion process로 이해될 수 있다.

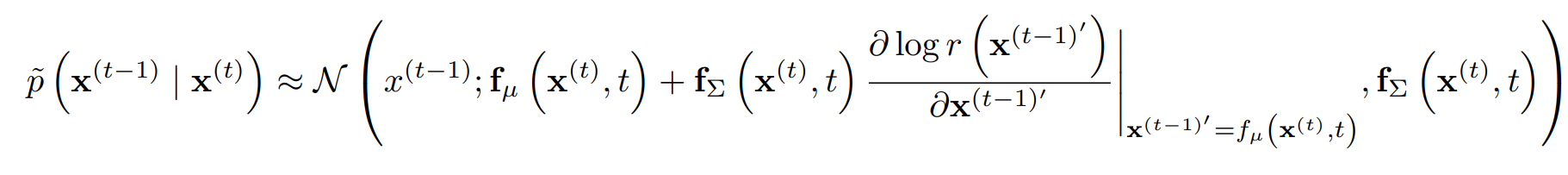
즉, 충분히 천천히 $r(x^{(0)})$으로 수렴하는 $r(x^{(t)})$를 사용하여 reverse diffusion process를 행하면 결과가 $p(x^{(0)})r(x^{(0)})$으로 천천히 수렴한다.