[2019 NIPS] Topology-Preserving Deep Image Segmentation

https://arxiv.org/pdf/1906.05404.pdf

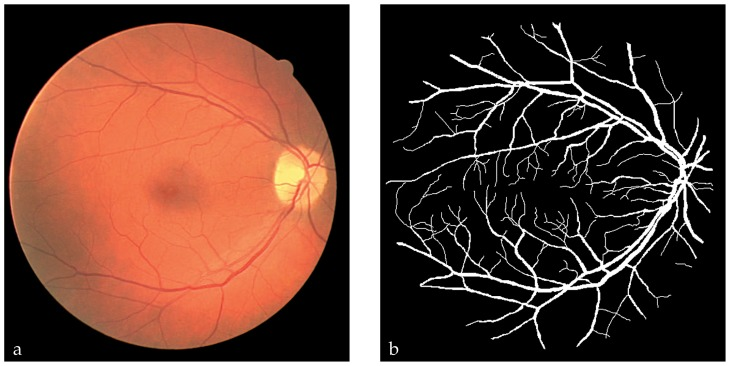
Image segmentation을 위해 일반적으로 사용되는 loss들에는 MSE loss, KL divergence, Cross entropy 등이 존재한다.
위의 loss들은 pixel-level accuracy로는 훌륭한 성능을 보여주지만, vessel segmentation등의 fine-scale structure를 예측하는 task에서는 아직도 error-prone한 모습을 보여준다.

위의 예시는 neuron image segmentation의 예시이다.
membrane의 connectivity가 제대로 예측된 경우엔 각 region을 정확히 나눌 수 있지만 (d), 작은 pixel단위의 오류만으로도 connectivity가 깨지고 region이 합쳐질 수 있다 (c).
따라서 이러한 task를 위해서는 pixel-level loss에 더해서 예측한 mask의 connectivity를 강제할 수 있는 loss가 필요하다.

Topology and connectedness

Neural network를 backpropagation을 통해 학습하기 위해서는 다음과 같은 조건이 필요하다.
1. 먼저, 원하는 특성을 measure할 수 있는 함수가 필요하다.
2. 그 함수가 미분가능해야한다.
위와 같은 경우는 connectivity를 measure하는 함수가 필요하고, 이를 통해 ground mask의 connectivity를 target으로 하여 학습하여야 할 것이다.

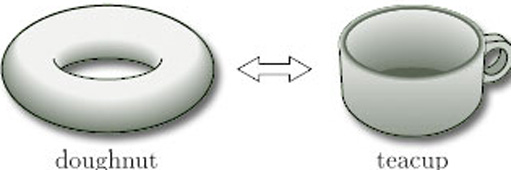
위상수학에 관심이 있는 사람이라면 '컵과 도넛은 위상 동형이다'라는 말을 들어보았을 것이다.
물론 두 대상은 기하학적으로는 다른 특성을 가지지만, 구조적인 특성 (구멍의 갯수, 연결된 component의 수 등... )은 동일하다는 뜻이다.
위상수학은 이렇듯 구조체들의 global한 특성을 분석하고 분류하는 데에 적절한 언어를 제공해준다.

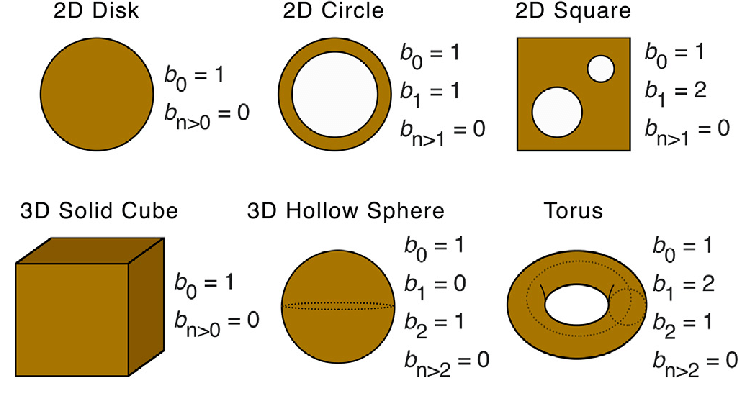
Betti number

Betti number이란 위상수학에서 물체의 n-차원 구멍의 갯수를 나타내는 숫자로, 0차원 Betti number는 connected component의 숫자를, 1차원 Betti number는 2차원 구멍의 수를 나타내고 2차원 Betti number는 빈 공간 (void)의 숫자를 나타낸다.
Betti number는 물체의 connectivity에 기반한 특성을 요약해주는 아주 좋은 지표이다.

요컨데 구 형태의 물체를 도넛형태의 물체로 바꾸고싶다면, 구 형태의 Betti number를 도넛 형태의 Betti number가 되게 하는 loss를 주면 되는 것이다.
문제는 Betti number는 discrete하기 때문에 (n=0,1,2,...) 미분이 불가능하다는 것이다.

Persistent Homology

Persistent Homology는 connectivity threshold의 변화에 따라 물체의 topology가 어떻게 변하는지를 요약하는 computational method이다.
Persistent homology에 대해 자세히 다루려면 대수위상적 지식이 필요하므로, 여기서는 간단히 예시를 통해 설명하겠다.

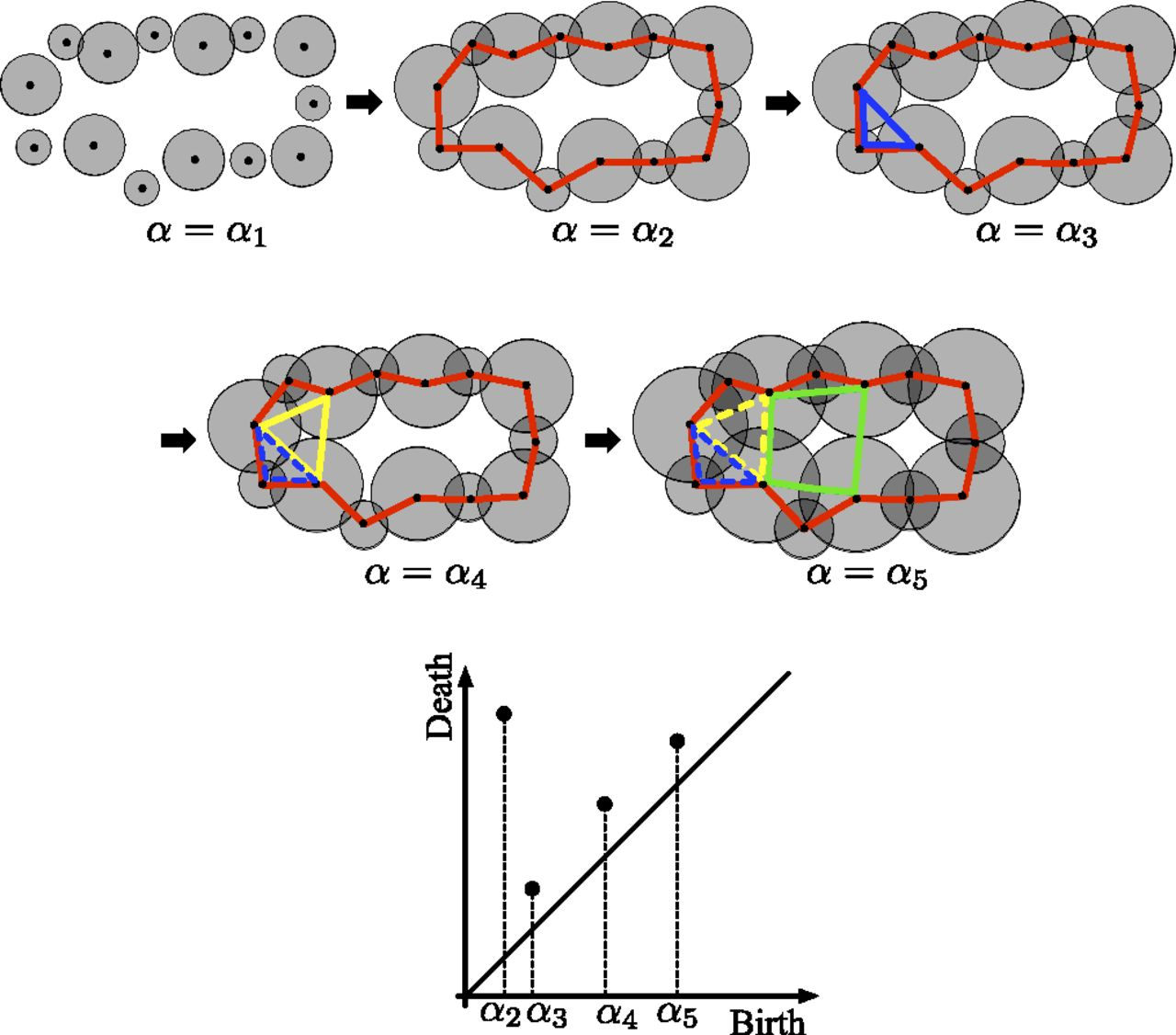
위의 사진은 threshold $\alpha$에 따라 1d-loop가 생기고 사라지는 양상을 나타낸 것이다.
먼저, $\alpha = \alpha_1$일 때는 아무런 loop가 생기지 않는다.
그 후 $\alpha = \alpha_2$일 때 커다란 빨간색 loop가 생성되어 $\alpha = \alpha_5$일때까지 살아남는다.
반면 $\alpha = \alpha_3$일 때 생성된 작은 파란색 loop는 $\alpha = \alpha_4$일때 소멸된다.
이와같은 결과가 아래의 persistent diagram에 나와있는데, Birth $= \alpha_2$에 대응되는 점이 Death $> \alpha_5$에 위치한 반면 Birth $= \alpha_3$일 때 대응되는 점은 Death $< \alpha_5$에 위치해있다.
이와 같이 빨간 loop는 오랫동안 지속되는 (persistent한) signal인데 반해 파란 loop는 금방 사라지는 (persistent하지 못한) signal이 된다.
일반적으로 persistent homology에서는 파란 loop와 같이 금방 사라지는 signal을 noise signal,빨간 loop와 같이 오래 지속되는 signal을 true signal으로 취급한다.
또한, 두 data point의 persisten diagram간의 true signal이 유사한 분포를 띠면, 두 data point가 유사하다고 취급한다.

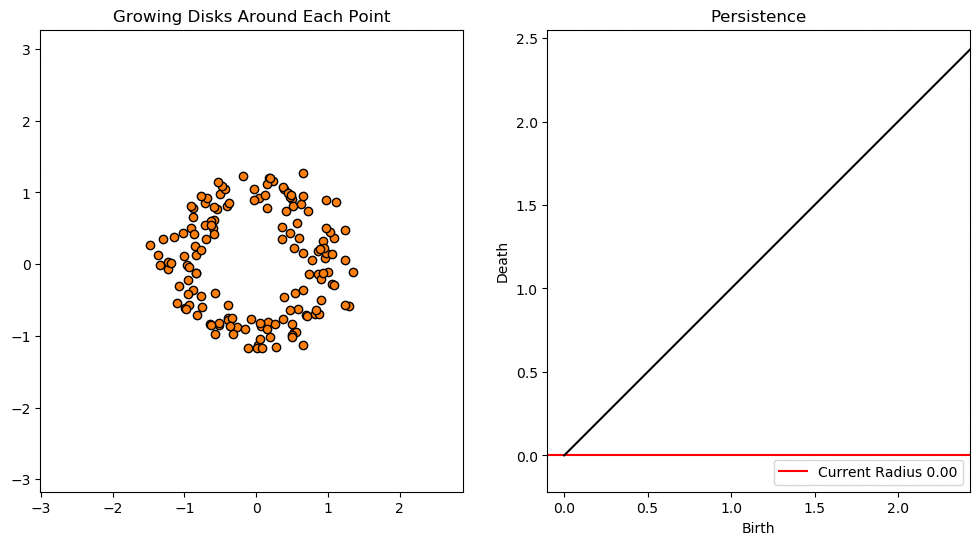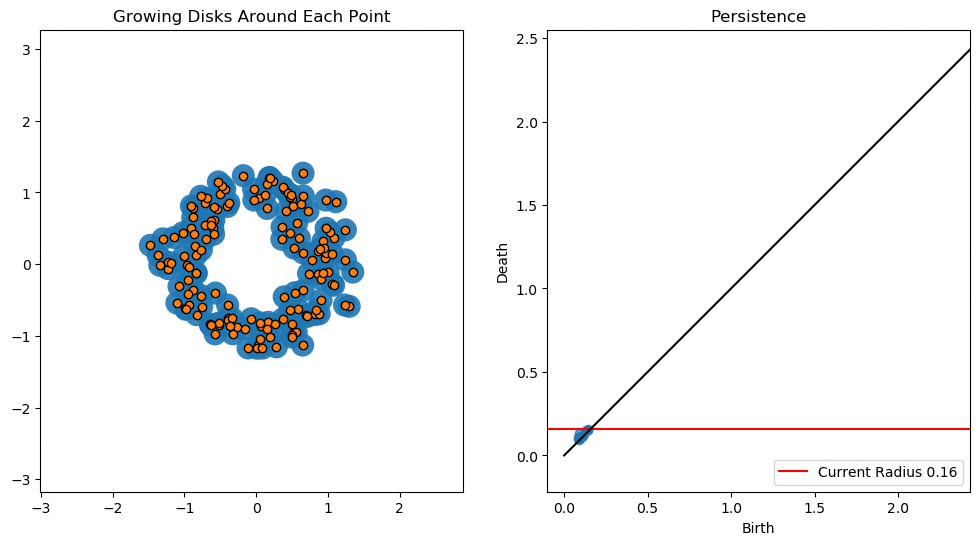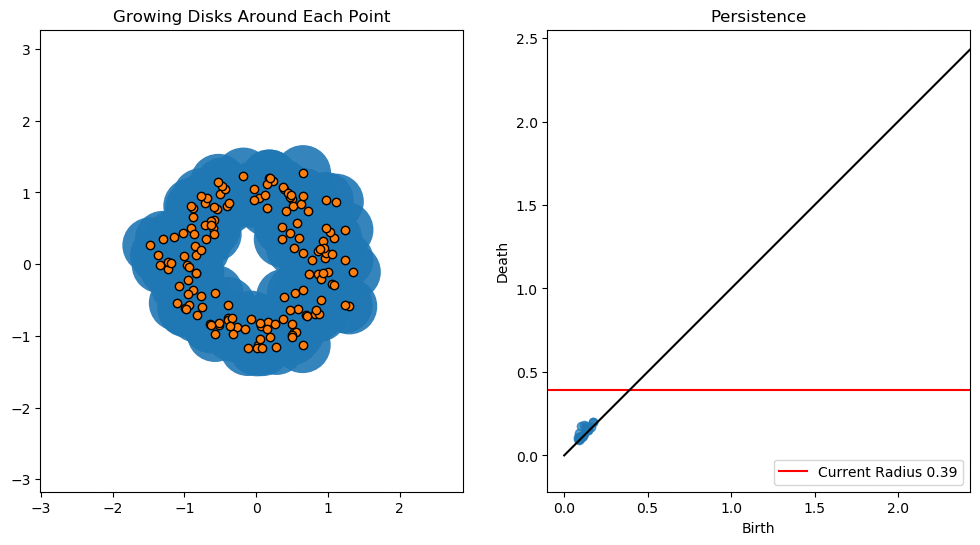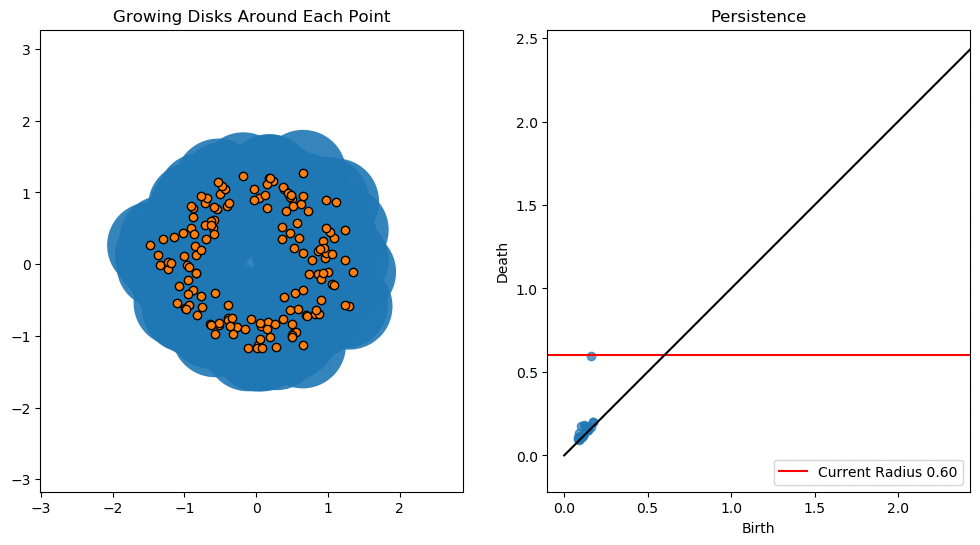
위의 gif파일은 threshold의 변화에 따른 도넛 모양 point cloud의 persistent diagram을 나타낸 것이다.
작은 loop들은 생성되는 즉시 소멸하여 $y=x$ 곡선에 가까이 분포한 반면, 큰 loop는 조금 더 오래 지속되어 $y=x$ 곡선의 위에 위치함을 알 수 있다.

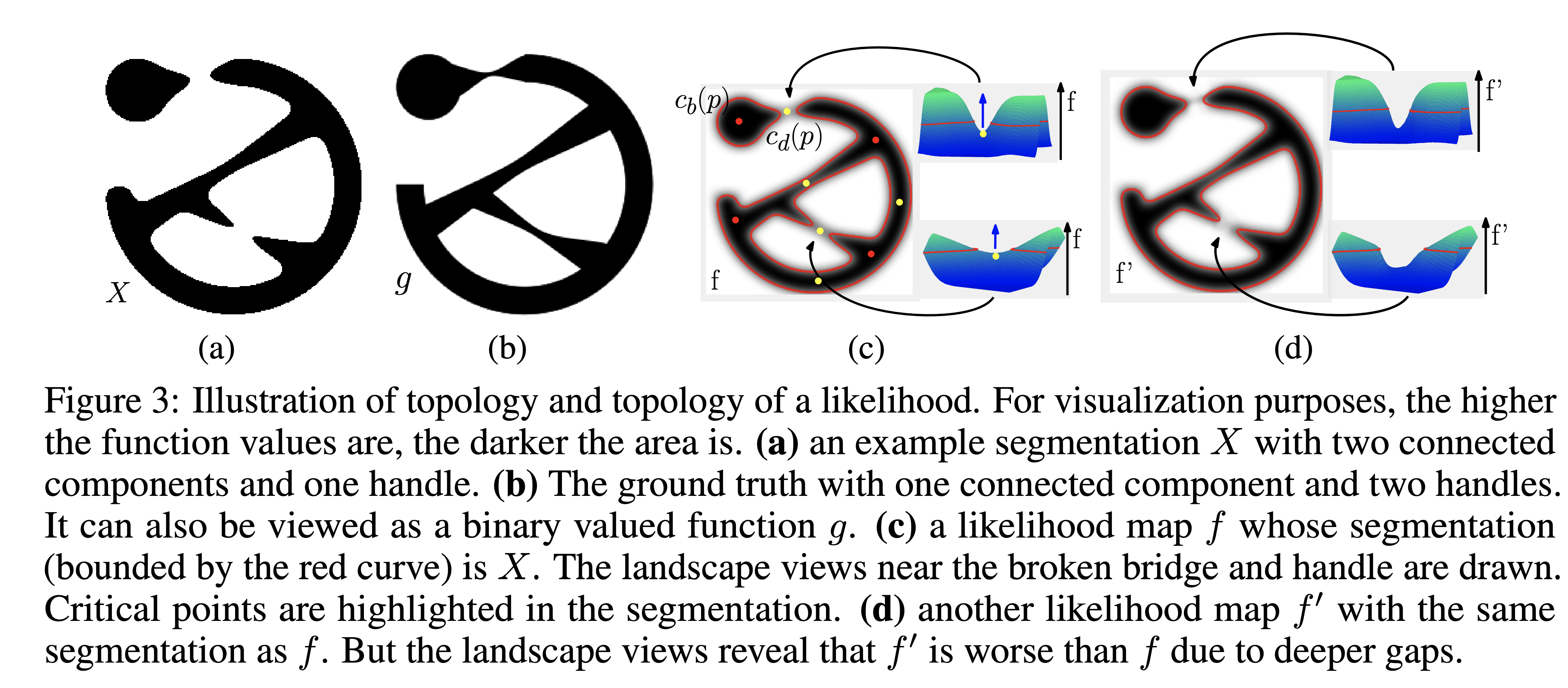
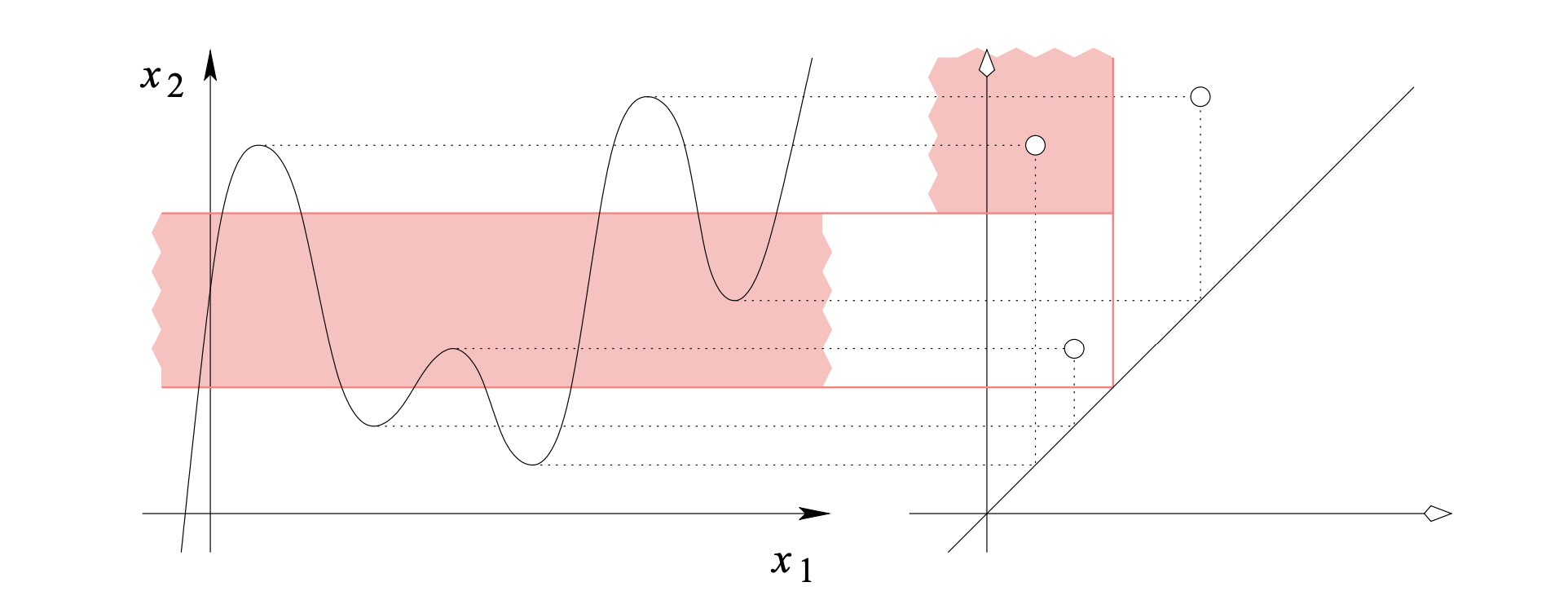
Persistent Homology of likelihood map

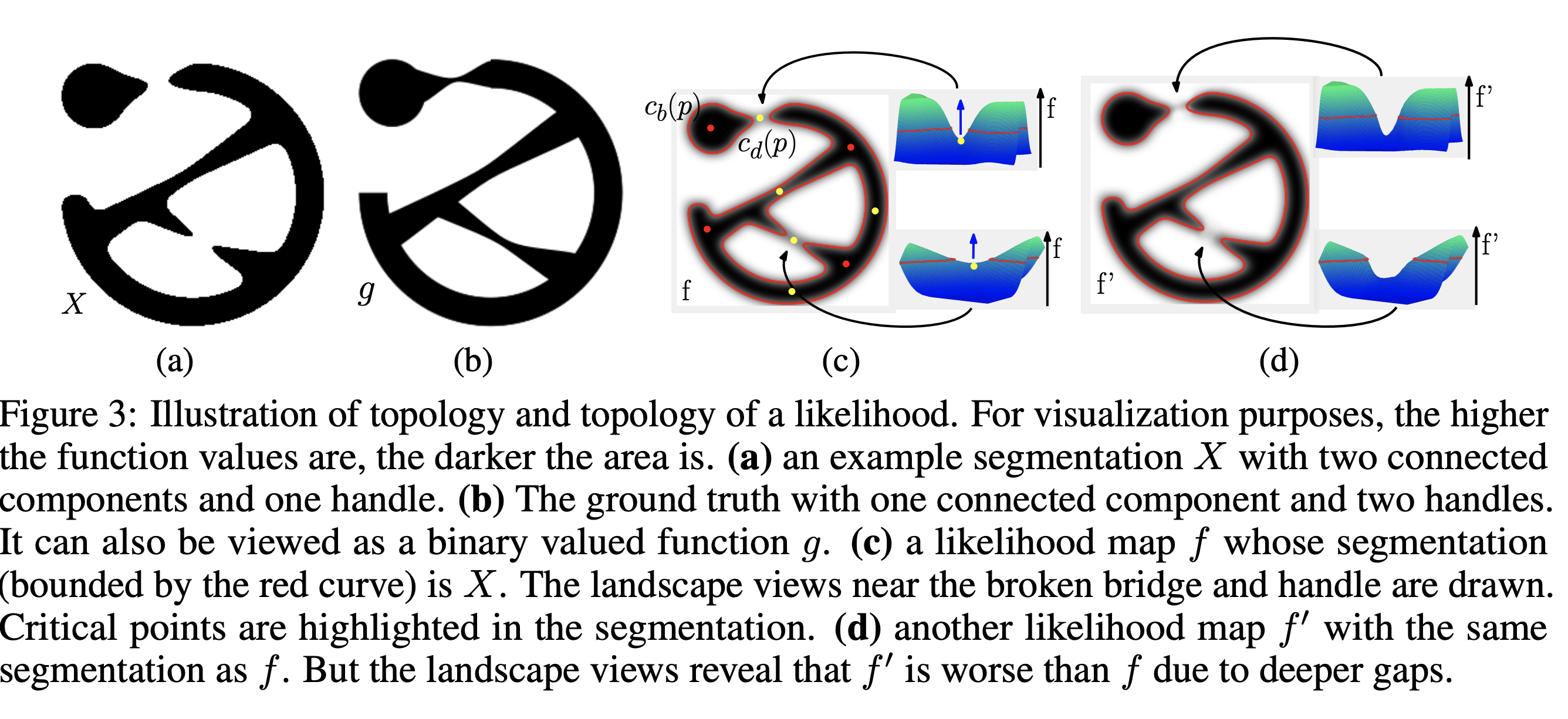
Ground truth map $g$와 threshold $\alpha = 0.5$에 대해 같은 segmentation mask $X$를 갖는 likelihood map $f$, $f'$가 주어졌다고 하자.
이 때 $f$, $f'$는 단순 binary mask로는 동일한 정확도를 가지지만, mask가 예측하지 못한 부분에서의 likelihood는 $f$가 $f'$보다 높으므로 f가 조금 더 좋은 likelihood map이라고 할 수 있다.
이와 같이 두 likelihood map을 비교하려면 특정 threshold $\alpha = 0.5$에서가 아닌 여러 threshold $\alpha_ \leq ... \leq \alpha_2 \leq \alpha_1$에서의 mask $f^{\alpha_1} \subseteq ... \subseteq f^{\alpha_2} \subseteq f^{\alpha_n}$를 비교할 필요가 있다.
이 때 persistent homology가 등장한다.

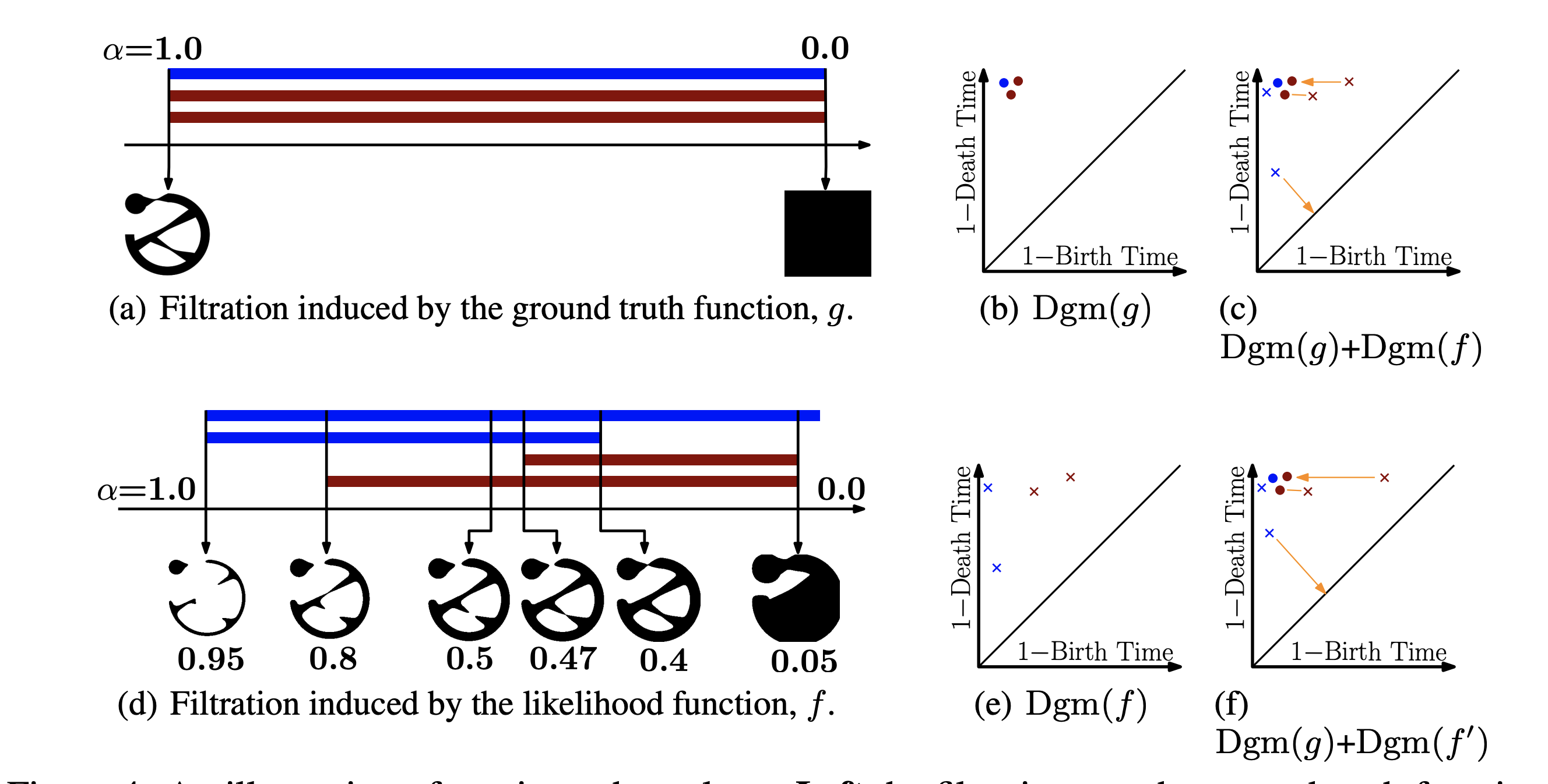
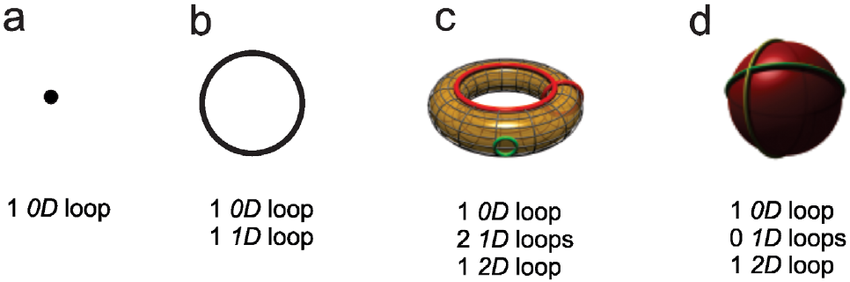
왼쪽의 diagram에서 파란색은 connected component (0d-loop), 갈색은 1d-loop의 threshold에 따른 birth time과 death time을 나타낸 것이다.
Persistent diagram에는 ground truth의 경우, connected component 1개 ($b_0 = 1$)와 1d-loop 2($b_1 = 2$)개가 존재하며, f에 대한 connected component 2개와 1d-loop 2개가 존재한다.
우리의 목표는 likelihood map f의 persistent diagram이 ground truth의 persistent diagram에 가깝게 만드는 것이다.
문제는 1. 두 diagram의 point의 갯수가 다르고 2. likelihood diagram의 각 점이 ground truth diagram의 어느 점에 대응되는지 알 수가 없다는 점이다.

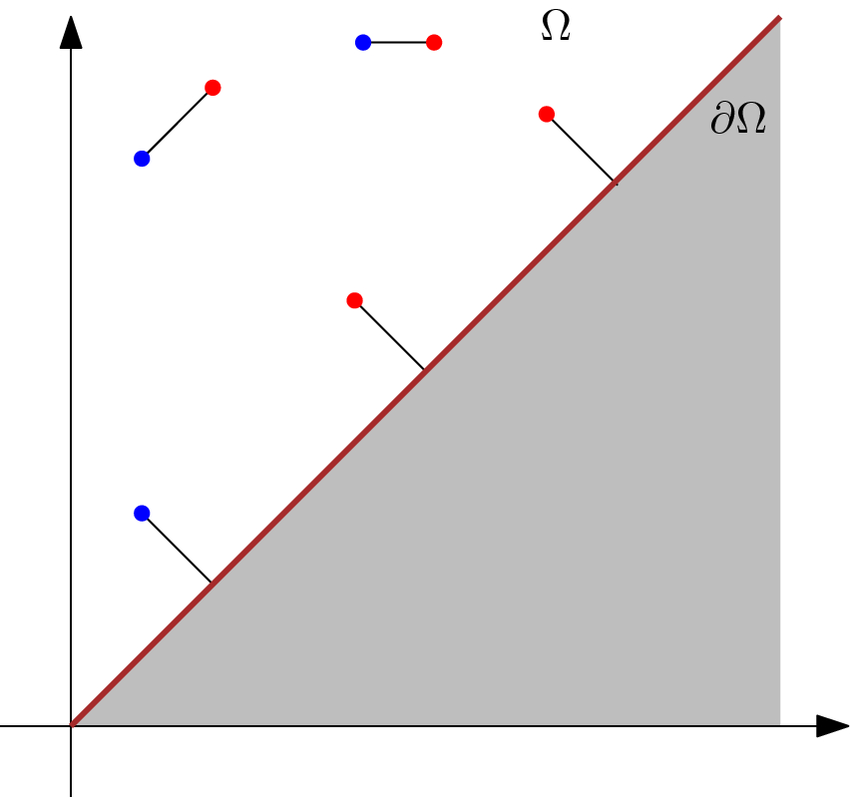
이를 해결하기 위해서는 Wasserstein distance에 기반한 matching algorithm이 사용된다.
즉, total squared distance가 최소화되는 1-1 matching을 찾은 후, 나머지 point들은 noise로 취급하여 $x=y$ 직선에 할당하는 것이다.

다행히도 위의 경우 ground truth diagram의 점들은 모두 (0,1)에 위치하므로 각 차원 Betti number만큼 (0,1)에 가까운 점들을 matching하고 나머지 점들은 $x=y$직선에 할당하면 된다.
이 때 $f'$에서의 loss가 $f$에서의 loss보다 확실히 큰 것을 알 수 있다.

Loss function은 다음이 된다.

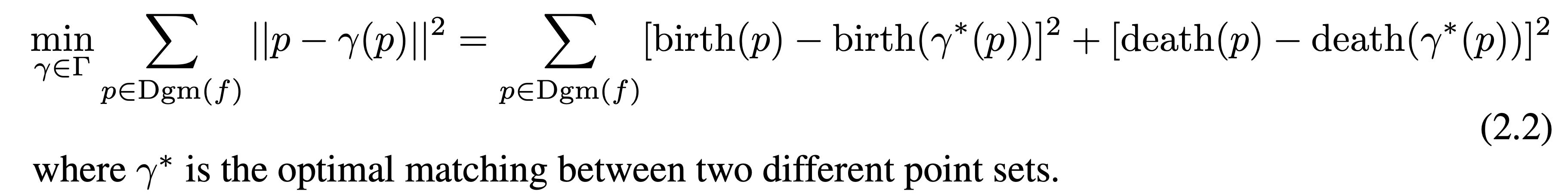
이 때 각 점 p의 좌표는 각 component의 birth/death에 의해 정해진다.
중요한 것은 f가 미분가능할 때 각 birth/death는 critical point (=critical pixel)에서만 일어난다는 것이다.

따라서 각각의 birth/death가 일어나는 critical point를 $c_b(p), c_d(p)$라고 하면 gradient는 다음이 된다.

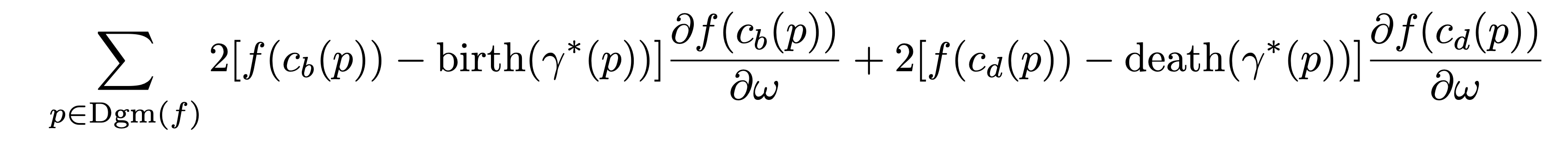
물론 $f(c_b(p)) = birth(p)$가 되는 점이 여러 군데 존재할 수 있으나, 그럴 확률은 0이기 때문에 무시하도록 한다.
gradient가 굉장히 적은 pixel에 대해서만 정의되어서 학습이 제대로 될까 싶었는데 결과가 상당히 괜찮다.