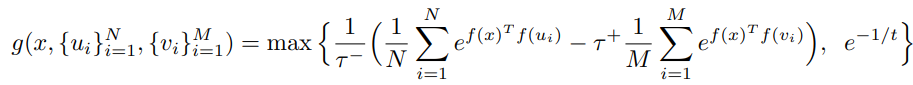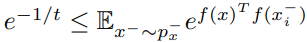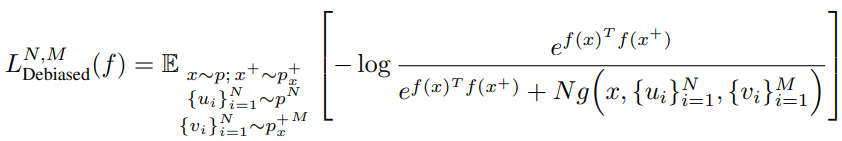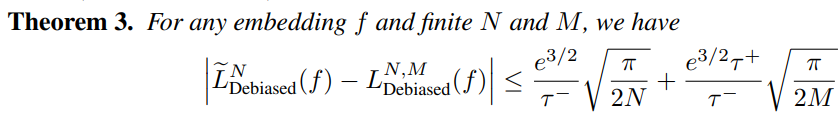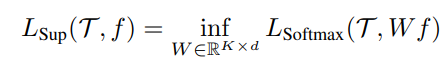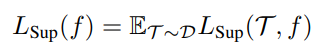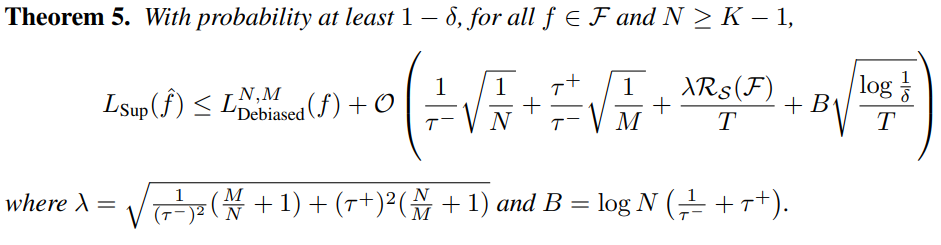https://proceedings.neurips.cc/paper/2020/file/63c3ddcc7b23daa1e42dc41f9a44a873-Paper.pdf

Contrastive learning

Superviesd learning을 하기 위해서는 데이터에 대응되는 정답 label이 필요하지만, 일반적으로 데이터에 대한 label을 구축하는 것은 힘든 작업입니다.
하지만 label이 존재하지 않더라도 데이터는 그 자체로 많은 정보를 담고 있습니다. 이를 이용하여 supervised learning에 도움을 줄 수는 없을까요?
Self-supervised learning이란 label이 주어지지 않은 데이터를 이용하여 네트워크를 사전학습하는 방법의 하나입니다.

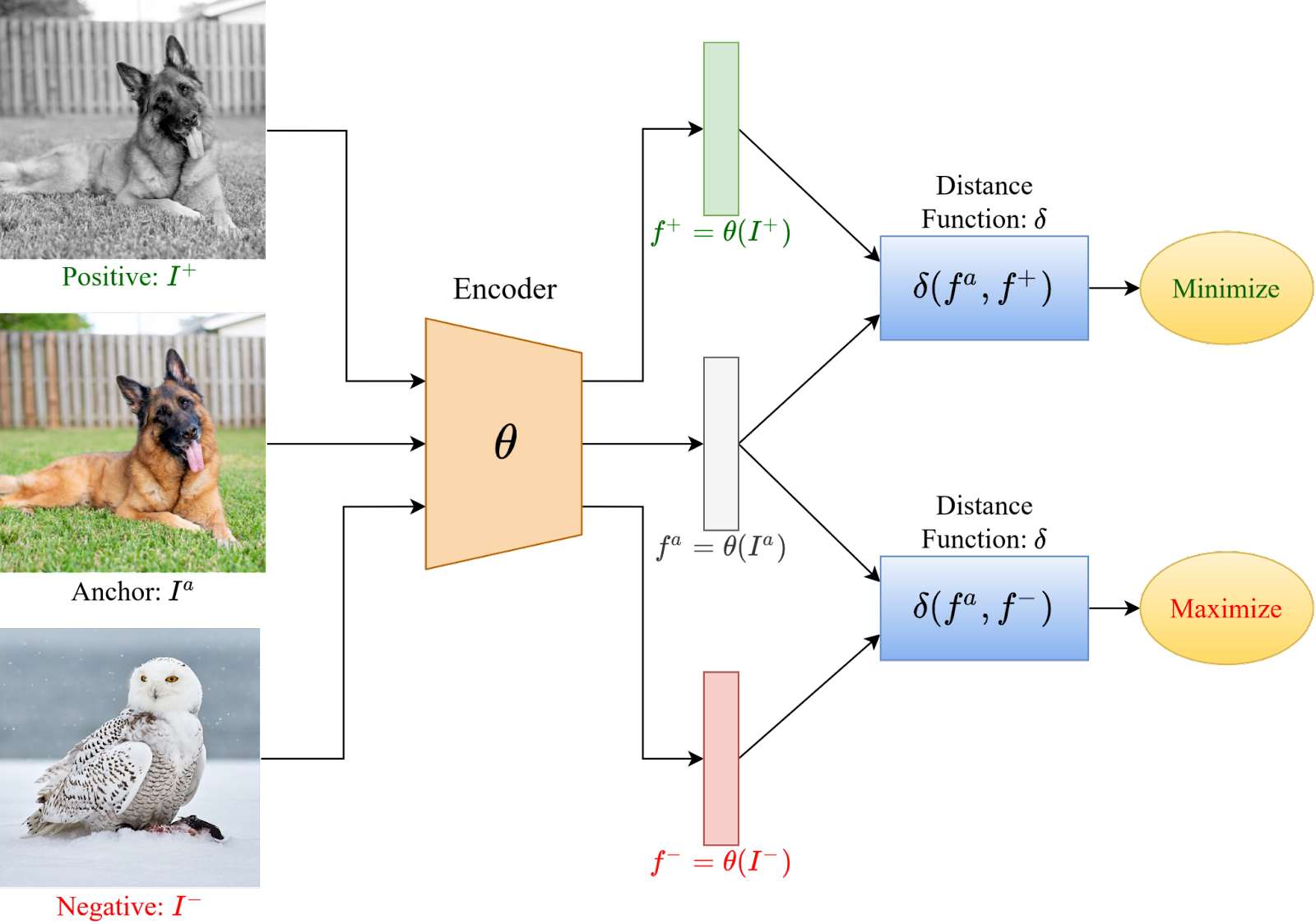
최근 많이 사용되는 기법의 하나는 Contrastive learning으로, '비슷한' 데이터간의 유사도는 높이고, '다른' 데이터간의 유사도를 낮추는 자가 학습을 통해 데이터를 구분하는 방법을 사전학습 하는 방법을 뜻합니다.

Label이 없는데 데이터가 비슷한지 다른지 어떻게 구분할까요?
일반적인 방식은 여러 장의 데이터에서 anchor data 한 장을 골라 augmentation을 한 사진을 postivie pair, 나머지를 negative pair로 두는 것입니다.
그 후 positive pair에 대한 유사성을 최대화하면서 negative pair에 대한 유사성을 최소화 하는 것이죠.

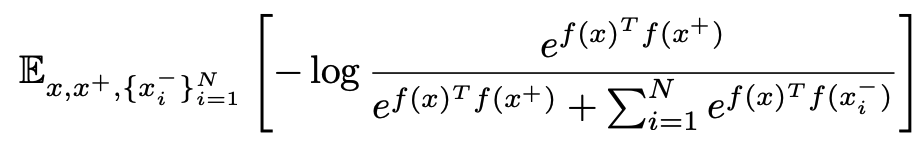
이를 수식적으로 나타내면 위와 같습니다.
먼저, 각 이미지를 encoder f(x)를 통해서 feature로 변환한 후 두 데이터간의 similarity를 두 feature간의 cosine similarity로 정의합니다.
이후 positive similarity에 대한 일종의 softmax를 최대화하는데, positive similarity가 커짐과 동시에 negative similarity가 작아져야 최대화가 가능합니다.

contrastive learning에서는 true negative가 아닌, positive anchor과 유사한 false negative pair를 repel하는 경우가 많습니다.
따라서 효과를 보기 위해서는 충분히 많은 데이터와 충분히 큰 배치 사이즈를 요구합니다.

이상적으로는, anchor과 같은 label을 가진 모든 false negative pair에 대한 부분을 loss의 분모에서 제외하는 것이 맞지만, 우린 label에 대한 정보가 없습니다.
그래서 이 논문에서는, class probability가 uniform하다는 가정 하에 false negative bias를 줄이는 방법을 제안합니다.

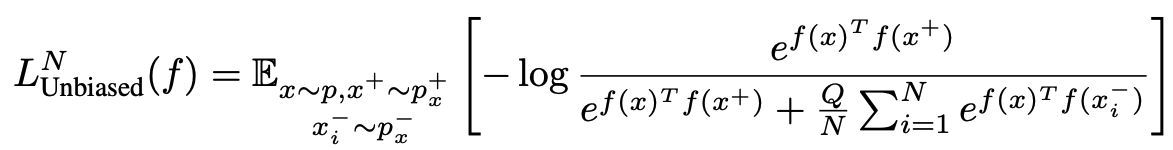
Bias가 없는 상황에서의 loss는 어떻게 될까요? 먼저 위의 수식에서 나오는 term들을 정의하겠습니다.
$p^-_x(x')$, $p^+_x(x')$는 각각 x'가 x의 true negative/true positive pair일 확률을 뜻합니다.
N은 negative pair의 갯수를, Q는 weight를 의미합니다. 일반적인 환경에서는 Q=N으로 설정되죠.
우리는 $p^-_x$에서 true negative를 sampling하여 false negative bias를 피하고 싶습니다.

문제는 우리는 $p^-_x$에 대한 정보가 없다는 것입니다. 따라서 앞서 말한대로 $p^-_x$ 대신 $p$에서 (possibly false) negative pair를 sampling합니다.
이 과정에서 false negative가 sampling되고, loss에 bias가 생기게 됩니다.

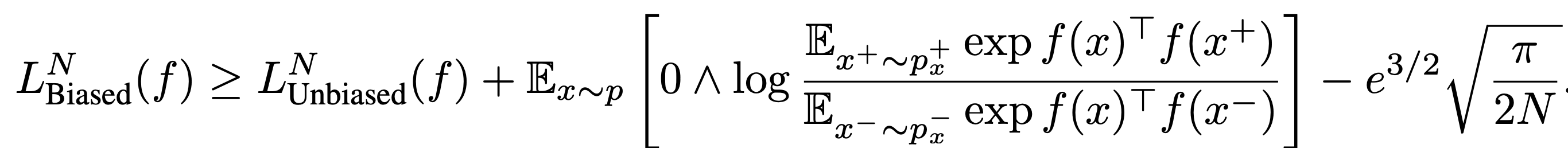
이 때 unbiased loss의 upper bound는 위와 같습니다.
MoCo등의 최근 방법들은 N = 65536등의 큰 숫자를 사용하기 때문에 마지막 항은 negligible합니다.
Biased loss가 upper bound를 정의하므로 biased loss를 최소화 함으로써 unbiased loss도 최소화할 수 있을 것 같습니다.
문제는 두 번째 항이 커질수록 upper bound까지의 gap이 커진다는 것입니다.

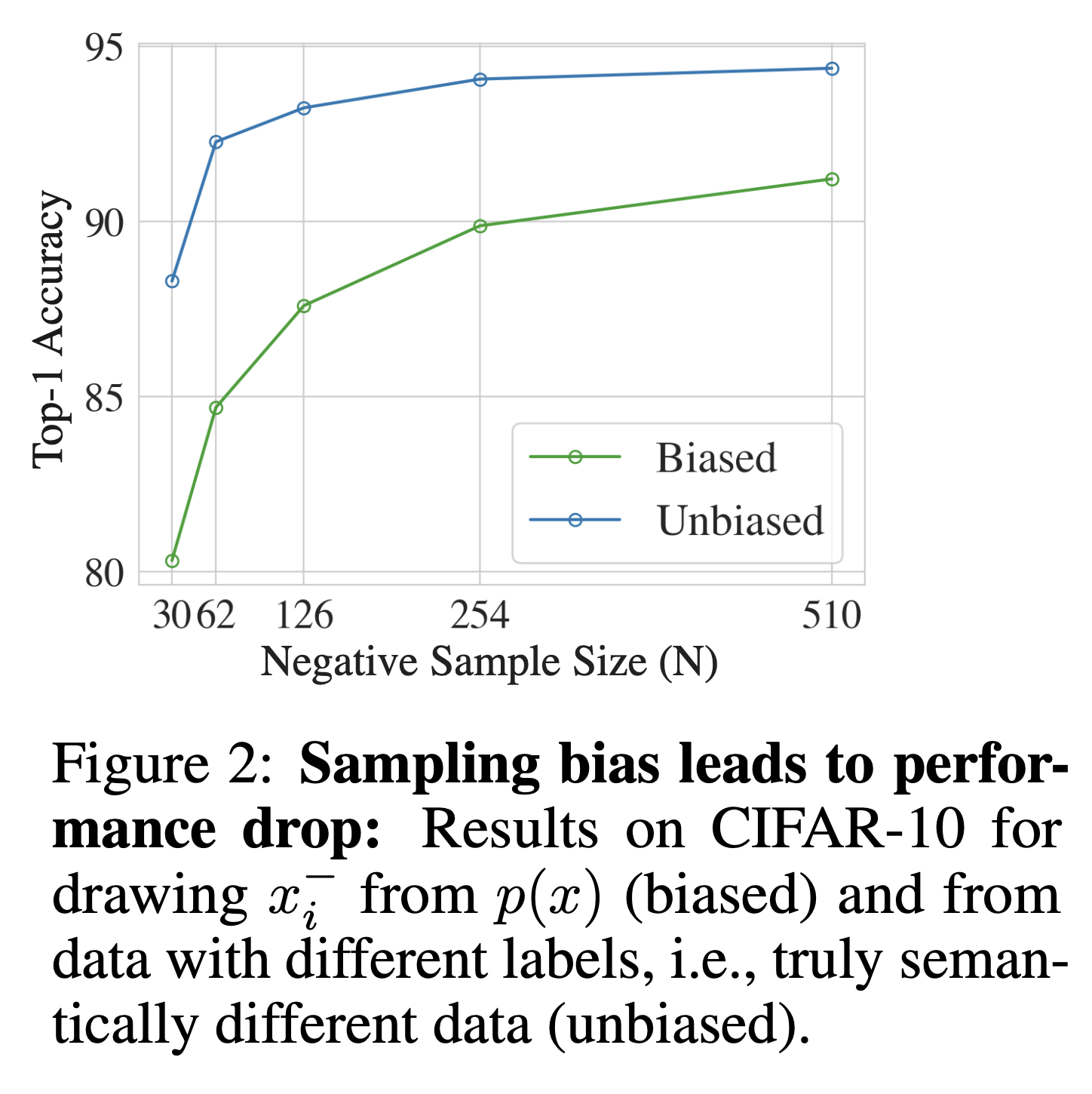
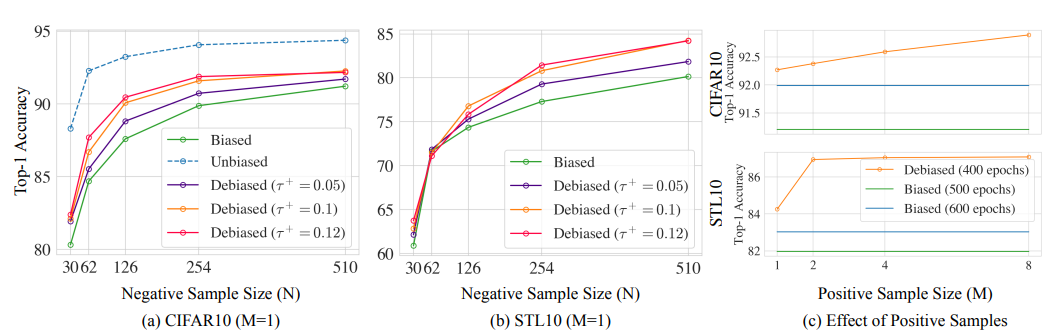
실제로 Cifar-10을 가지고 학습을 하였을 때, top-1 accuracy에 대해서 unbiased/biased loss에 대한 결과가 차이나는 것을 보아 empirical하게 두 loss간에는 큰 차이가 난다는 것을 알 수 있습니다.
따라서 위의 부등식은 딱히 reliable한 관계를 주지는 못합니다.

이 논문에서는 class probability에 대한 prior를 통해 더 낮은 bias를 가지는 loss estimator를 찾습니다.
조금 더 자세히 말하면, negative pair 중 positive pair의 갯수가 몇 개인지에 따른 risk를 class probability prior를 통해 근사하는 것입니다.

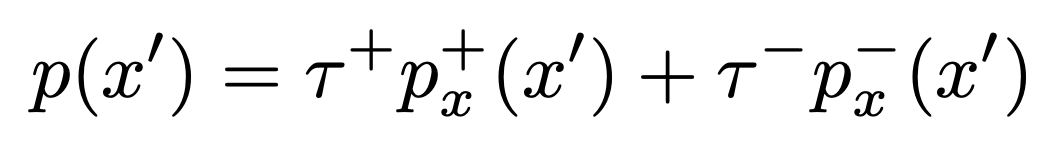
먼저, data distribution을 위와같이 decompose합시다. (둘의 support는 disjoint하다고 가정하는 것 같습니다)

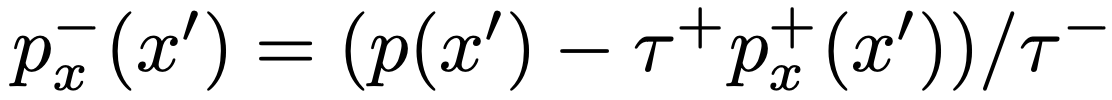
위와 같은 decomposition 하에서 $p^-_x$는 $p^+_x$를 통해 얻어낼 수 있습니다.
위의 관계를 이용하여, expectation에 있는 $p^-_x$를 altertnative form으로 쓰면 $p$, $p^+_x$에 대한 접근만을 통해 $p^-_x$에서의 sampling을 근사할 수 있지 않을까요?

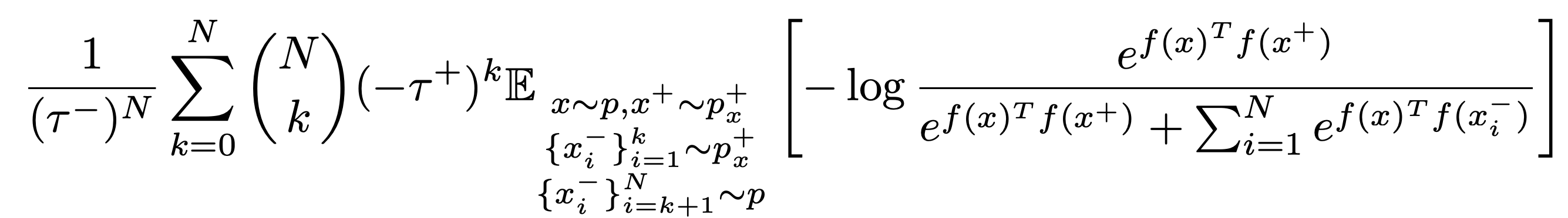
안타깝게도 위의 식은 모든 combination에 대해 expectation의 estimate를 요구하므로 computationally expensive할 뿐더러, 최소 N개의 positive sample이 존재해야만 exact한 estimate가 됩니다.
따라서 위의 식을 direct하게 최소화 하는 대신 negative example (true negative + false positive)의 수 N이 커짐에 따라 unbiased estimator가 asymptotic하게 근사하는 분포를 찾습니다.

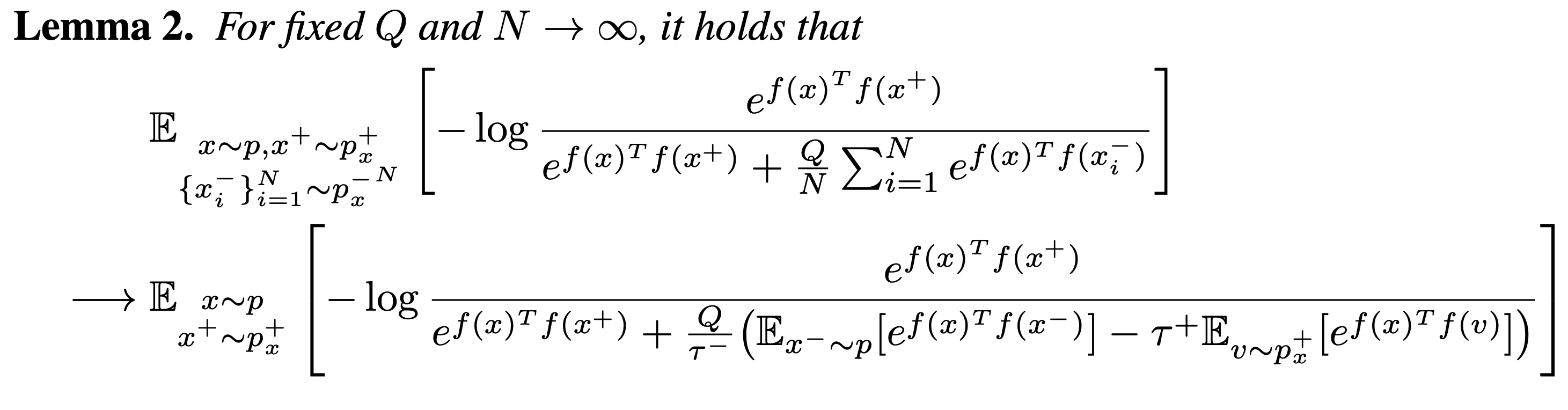
이 식은 여전히 $x^-$를 $p$에서 샘플링하지만, additional positive sample v를 추가하여 둘의 weight를 조정합니다.

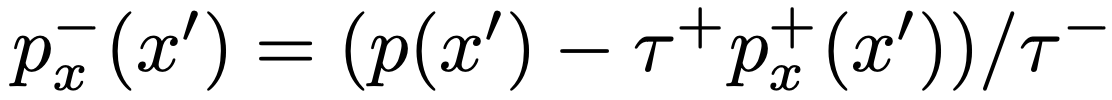
이는 또한 위에서 본 $p^-_x$의 indirect한 expression을 사용한 것으로, $p^+_x$와 $p$에 대한 expectation이 큰 expectation의 안으로 들어가면서 각각의 estimate가 decoupled되었다는 장점이 있습니다.

실제로 asymptotic distribution의 분모에 있는 두 번째 항을 empirical하게 계산하는 과정에서는 위의 식을 사용합니다.
이 때 $u_i$는 데이터 샘플, $v_i$는 augmented anchor에 해당합니다.
개인적으로는 $p^+_x$의 분포와 augmented anchor들의 분포가 다르기 때문에 여기서 논리의 비약이 있지 않나 싶습니다만, 이 정도로도 성능의 증가를 정당한 논리적 근거를 통해 이뤄냈으니 본인들은 만족한다고 합니다.
이 때 $e^{-1/t}$의 lower bound를 둔 것은

식 안의 값이 negative가 되는 것을 방지하기 위해서 theoretical minimum으로 bound 한 것입니다.
(t가 갑자기 나오셔서 당황하셨을 수도 있는데, contrastive learning에 종종 사용되는 temperature입니다. 논문에서 t=1로 두고 논리를 전개하겠다고 하였는데 갑자기 튀어나왔네요.)

Q=N으로 두면 empirical loss는 위와 같이 정의됩니다.

Asymptotic loss의 empirical loss에 대한 error bound는 위와 같습니다.
N과 M이 늘어나면 emprical expectation의 정확도도 올라가고, 따라서 오차가 줄어든다고 볼 수 있겠네요.

실제로 N-batch와 M-positive pair에 대한 ablation study 결과를 보았을 때 N과 M의 증가에 따라서 성능 증가가 따라오는 것을 볼 수 있죠.

위에서 살펴본 것은 이 empirical loss가 asymptotic loss를 근사한다는 것, 그리고 N과 M의 증가에 따라 성능이 증가한다는 것 뿐이었습니다.
Empirical하게 negative bias가 줄어든 결과라고 말할 순 있겠지만, 실제로 그런지 이론적 분석 또한 뒷받침 되어야 할 것입니다.

먼저, 이 논문에서는 encoder의 특정 classification task에 대한 성능을 encoder를 freeze했을 때 linear classifier를 통해 얻을 수 있는 성능의 최댓값으로써 정의합니다.

또한 encoder의 자체 성능을 일반적인 classification task에 대한 성능의 기댓값으로써 정의합니다.

이 때 optimal backbone에 대한 upper bound는 다음과 같습니다.
우리가 주장하였듯 데이터셋의 크기 T, example의 수 N, positive pair의 수 M등이 커질수록 optimal loss에 대한 bound가 작아집니다.