썸네일은 공부하면서 도움된 것 및 즐겁게 본 것을 추린 것이다. (감사)

학습 목적 및 배경

양자 정보 이론 및 양자 컴퓨팅에서 Mixed States는 매우 중요하게 다루어지지만, 그 컨셉과 수학적 구조 모두 받아들이기 쉽지 않다. Quantum Computing의 기초 원리를 이해하는 것이 주 학습목적이고, 더 나아가서 그 이해를 다른 사람에게 이해하기 쉽게 전달 할 수 있는 기본기를 확보하고 싶다. 그리고 양자정보이론 분야가 나에게 재미있게 느껴질 뿐만 아니라 (나에게 있어서 새롭지만) 연구에 매진할 가치가 있는지 판단하고자 한다. 필자는 이 분야와 전혀 상관 없는 사람이지만, 메우 우연한 기회로 해당 분야에 대해 공부할 이유가 생겼고 공부하다 보니 이에 흥미가 크게 생겼다. 구체적으로 양자역학이 자체가 아니라, 양자역학을 이용한 암호키 분배 솔루션이 정말로 무조건적으로 안전한게 맞는지 관심이 생겼다. 쉬운 예를들어서, (광자를 이용한 대칭키 분배 프로토콜인) BB84의 경우 (특정 조건이 걸린) 광자를 하나씩만 보내는 방식으로 정보를 전달한다. 정말로 광자가 하나씩 보내지는 경우에 한해서는 무조건 적인 안전이 보장되며, 우연히 같은 상태의 광자를 여러개 보내는 경우 그 것을 탈취하는 방식의 도청에 대한 위험은 여전히 존재한다. 즉, 도청자 입장에서 정보보호가 필요한 정보(분배하고자 하는 키 정보)의 일부를 얻을 수 있다는 것이다. 따라서 어느 정도의 위험도가 있는지 명확히 정의하고 그 위험도가 프로토콜 전체에 미치는 영향에 대한 통계적 결론을 내려줄 필요가 있다.

Mixed State를 활용한 대칭키 분배 프로토콜과 그 것의 안정성에 대한 관심이 있다. 그러나, 이 관심을 끝까지 따라가고 시간을 매우 투자하여 깊게 공부하는 것이 좋을 지(이러려면 진학이 필요한 상황이 될거라 본다.), 지금처럼 취미로 훝어보기만 하는게 좋을지는 아직 판단하지 않고 보류중이다.

힐버트 공간의 정의

---

복소내적공간(complex inner product space)은 복소수(complex number) 체(field) 위에 정의된 벡터공간(vector space)으로, 내적(inner product)이라는 특별한 이항 연산을 갖는다.

정의: 내적이란 다음 성질들을 만족하는 이항연산이다.

1. 켤레 대칭성(conjugate symmetry):
   모든 벡터 $x, y$에 대해, 내적 $\langle x, y \rangle$는 다음을 만족한다.

   $\langle x, y \rangle = \overline{\langle y, x \rangle}$

   여기서 $\overline{\langle y, x \rangle}$는 $\langle y, x \rangle$의 복소켤레(complex conjugate)이다.

2. 선형성(linearity in the first argument):
   모든 벡터 $x, y, z$와 복소수 $a, b$에 대해, 내적은 다음을 만족한다.
   $\langle ax + by, z \rangle = a \langle x, z \rangle + b \langle y, z \rangle$
   여기서 첫 번째 인수에 대해 선형(linear)이며, 두 번째 인수에 대해 켤레-선형(conjugate linear)이다.

3. 켤레-선형성(conjugate linearity in the second argument):
   모든 벡터 $x, y, z$와 복소수 $a, b$에 대해, 내적은 다음을 만족한다.
   $\langle z, ax + by \rangle = \overline{a} \langle z, x \rangle + \overline{b} \langle z, y \rangle$
   여기서 $\overline{a}$와 $\overline{b}$는 각각 $a$와 $b$의 복소켤레(complex conjugate)이다.

4. 양의 정부호성(positive definiteness):
   모든 벡터 $x$에 대해, 내적은 다음을 만족한다.
   $\langle x, x \rangle \geq 0$
   그리고 $\langle x, x \rangle = 0$이면 $x = 0$이다.

복소내적공간의 예로는 힐버트 공간(Hilbert space)이 있다. 힐버트 공간은 완비성을 추가로 만족하는 내적공간이다. 완비성은 벡터공간의 모든 코시 수열(Cauchy sequence)이 공간 내에서 수렴하는 성질을 의미한다.

유한차원 내적 공간은 언제나 힐버트 공간이다.

디랙 표기법을 사용할 경우, 내적은 다음과 같이 표기된다:
$\langle y | x \rangle$

---

연습: 힐버트 공간에서 곱집합과 텐서곱집합의 내적 정의

문제 1: 벡터 공간의 곱집합에서의 내적

벡터 공간 $V$와 $W$가 각각 복소내적공간이라고 하자. 이때 $V \times W$는 벡터 공간 $V$와 $W$의 곱집합(cartesian product)으로 정의된다. 곱집합 $V \times W$ 위에 내적을 제시하라.

특별한 언급이 없으면, 다음과 같이 정의한다.

$\langle (v_1, w_1), (v_2, w_2) \rangle_{V \times W} = \langle v_1, v_2 \rangle_V + \langle w_1, w_2 \rangle_W$
여기서 $\langle \cdot, \cdot \rangle_V$는 $V$ 위의 내적이고, $\langle \cdot, \cdot \rangle_W$는 $W$ 위의 내적이다.

연습문제
1. 위의 내적이 $V \times W$에 대해 내적공간의 성질(켤레 대칭성, 선형성, 양의 정부호성)을 만족함을 보이라.

문제 2: 벡터 공간의 텐서곱집합에서의 내적

벡터 공간 $V$와 $W$가 각각 복소내적공간이라고 하자. 이때 $V \otimes W$는 벡터 공간 $V$와 $W$의 텐서곱(tensor product)으로 정의된다. 텐서곱 $V \otimes W$ 위에 내적을 제시하라.

상당히 중요한 문제이므로, 꼭 고민해보길 추천한다.

특별한 언급이 없으면, 다음과 같이 정의한다.

$\langle v_1 \otimes w_1, v_2 \otimes w_2 \rangle_{V \otimes W} = \langle v_1, v_2 \rangle_V \cdot \langle w_1, w_2 \rangle_W$
여기서 $\langle \cdot, \cdot \rangle_V$는 $V$ 위의 내적이고, $\langle \cdot, \cdot \rangle_W$는 $W$ 위의 내적이다.

질문:
위의 내적이 $V \otimes W$에 대해 내적공간의 성질(켤레 대칭성, 선형성, 양의 정부호성)을 만족함을 보이라.

사적 생각:
위에 주어진 내적이 내적임을 보이는 것보다, 그냥 아 나라면 어떻게 텐서곱공간에 내적을 줄까?를 고민하다가 깨닫는게 훨씬 유익함.

---

힐버트 공간의 정규직교 기저

정의 및 성질

정규직교 기저 (Orthogonal Basis)

• 유한 차원 힐버트 공간: 유한 차원 힐버트 공간 $H$에서는 직교기저를 구성할 수 있으며, 이 기저는 모든 벡터가 직교하고 각각의 벡터의 길이가 1인 경우 정규직교기저가 된다. 즉, 기저 $\{e_1, e_2, \ldots, e_n\}$는 다음 성질을 만족한다:
  $\langle e_i, e_j \rangle = \delta_{ij}$
  여기서 $\delta_{ij}$는 크로네커 델타로, $i = j$일 때 1, 그렇지 않을 때 0이다.

• 무한 차원 힐버트 공간: 무한 차원 힐버트 공간에서도 정규 직교기저를 정의할 수 있으며, 이 경우 정규직교기저는 다음과 같이 정의된다. 정규직교기저 $\{e_n\}$는 $H$의 모든 벡터 $x$에 대해 다음을 만족한다:
  $x = \sum_{n=1}^{\infty} \langle x, e_n \rangle e_n$
  여기서 $\langle x, e_n \rangle$는 $x$와 $e_n$의 내적이며, 이 급수는 $H$에서의 노름에 대해 수렴한다.

  무한차원 힐버트 공간의 정규직교 기저는 무한 선형 결합을 정의상 요구한다. 이는 벡터 공간의 기저의 존재성 및 차원의 유일성을 논할 때말하던 그 기저가 아니다. 조금만 주의하여 디테일을 챙겨가자.
  디테일을 채운 독자의 흥미를 돋구기 위해서 다음 명제들을 제시한다.
  1. 바나흐 공간(complete normed vector space)은 가산 무한 기저를 가질 수 없다.
  2. 분해 가능 힐버트 공간은 가산 정규 직교 기저를 가진다.
  3. 물론, 분해 가능 (무한 차원) 힐버트 공간은 바나흐 공간이다. 그러나 위의 두 문장(1,2)는 상충하지 않는다. 1.에서 말하는 기저는 유한 선형 결합을 정의상 요구하는 기저이고 2.에서 말하는 기저는 (가산) 무한 선형 결합을 정의상 요구하는 (힐버트 공간의) 정규 직교 기저이다.
  4. 유한 선형 결합을 정의상 요구하는 경우와 그렇지 않은(무한 선형 결합) 경우를 구별하기 위해서, 전자를 하멜 기저 후자를 Schauder 기저라고 부른다.
  5. 주어진 힐버트 공간의 모든 정규 직교 기저는 같은 크기(cardinality)를 가진다. 이를 힐버트 차원(Hilbert dimension)이라 부른다.
  6. 힐버트 차원은 벡터공간의 차원( 하멜 기저의 크기(cardinality))와 일반저으로 다르다. 물론, 유한차원 힐버트 공간의 경우 동일하다.
  7. 힐버트 차원이 같은 두 힐버트 공간은 isomorphic하다.
  8.힐버트 공간 isomorhpism은 벡터 공간 isomorhpism이다. 따라서, 두 힐버트 공간이 같은 힐버트 차원을 가지면 같은 (하멜) 차원을 가진다.
  9. 바로 직전 문장(8.)의 역은 성립하지 않는다. 다시 말해서, 힐버트 차원이 다르지만 (하멜) 차원이 동일할 수 있다.

연습문제: 힐버트 공간의 정규직교 기저

문제 1: 힐버트 공간의 정규직교 기저 존재 증명

문제 1: 모든 힐버트 공간에 정규 직교 기저가 존재함을 증명하라. 이 문제의 조건에 유한차원 조건을 추가로 걸고, 다음 단계에 따라 문제를 해결하시오.
1. 힐버트 공간 $H$의 임의의 벡터 $x \in H$를 취하라.
2. 그라미-슈미트 정규직교화 과정(Gram-Schmidt orthogonalization process)을 사용하여 $H$에서 정규직교 기저를 구성하라.
3. 구성된 정규직교 기저가 $H$의 모든 벡터를 나타낼 수 있음을 보이시오.

문제 2: 곱집합 및 텐서곱공간의 정규직교기저 찾기

문제 2: 벡터 공간 $V$와 $W$가 각각 힐버트 공간일 때, $V \times W$와 $V \otimes W$의 정규직교기저를 구하시오.

1. 곱집합 $V \times W$에서의 정규직교기저:
   • $V$의 정규직교기저를 $\{v_i\}$, $W$의 정규직교기저를 $\{w_j\}$라고 하자.
   • $V \times W$에서의 정규직교기저를 $(v_i, 0)$과 $(0, w_j)$ 모임으로 제시 하고, 다음을 확인하시오.

     $\langle (v_i, w_j), (v_k, w_l) \rangle := \langle v_i, v_k \rangle_V + \langle w_j, w_l \rangle_W$이라 할때, 제시한 집합은 정규직교를 이룬다.

2. 텐서곱공간 $V \otimes W$에서의 정규직교기저:
   • $V$의 정규직교기저를 $\{v_i\}$, $W$의 정규직교기저를 $\{w_j\}$라고 하자.
   • $V \otimes W$에서의 정규직교기저를 $v_i \otimes w_j$의 모임으로 제시하고, 다음을 확인하시오.

     $\langle v_i \otimes w_j, v_k \otimes w_l \rangle := \langle v_i, v_k \rangle_V \cdot \langle w_j, w_l \rangle_W$이라 할때, 제시한 집합은 정규 직교를 이룬다.

텐서곱 예시: 두 2차원 및 3차원 복소내적벡터 공간

두 힐버트 공간 $V = \mathbb{C}^2$와 $W = \mathbb{C}^3$를 고려하자. 이 벡터 공간의 표준 기저는 다음과 같다:
$V = \text{span}\{e_1, e_2\}, \quad W = \text{span}\{f_1, f_2, f_3\}$

여기서
$e_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$, $e_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}$,

$f_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$, $f_2 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$, $f_3 = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$.

그리고, 각 공간 $V,W$의 내적이 표준적으로 주어졌다고 가정하자. 즉, 표준기저들이 곧 정규직교 기저이다. 다시말해서,

$V$의 내적:
$\langle e_i, e_j \rangle_V = e_i^\dagger e_j$

$W$의 내적:
$\langle f_i, f_j \rangle_W = f_i^\dagger f_j$

이때, 두 힐버트 공간 $V$와 $W$의 텐서곱 $V \otimes W$는 다음과 같은 정규 직교기저를 가진다.
$\{e_1 \otimes f_1, e_1 \otimes f_2, e_1 \otimes f_3, e_2 \otimes f_1, e_2 \otimes f_2, e_2 \otimes f_3\}$

그림으로 나타내면 다음과 같다.

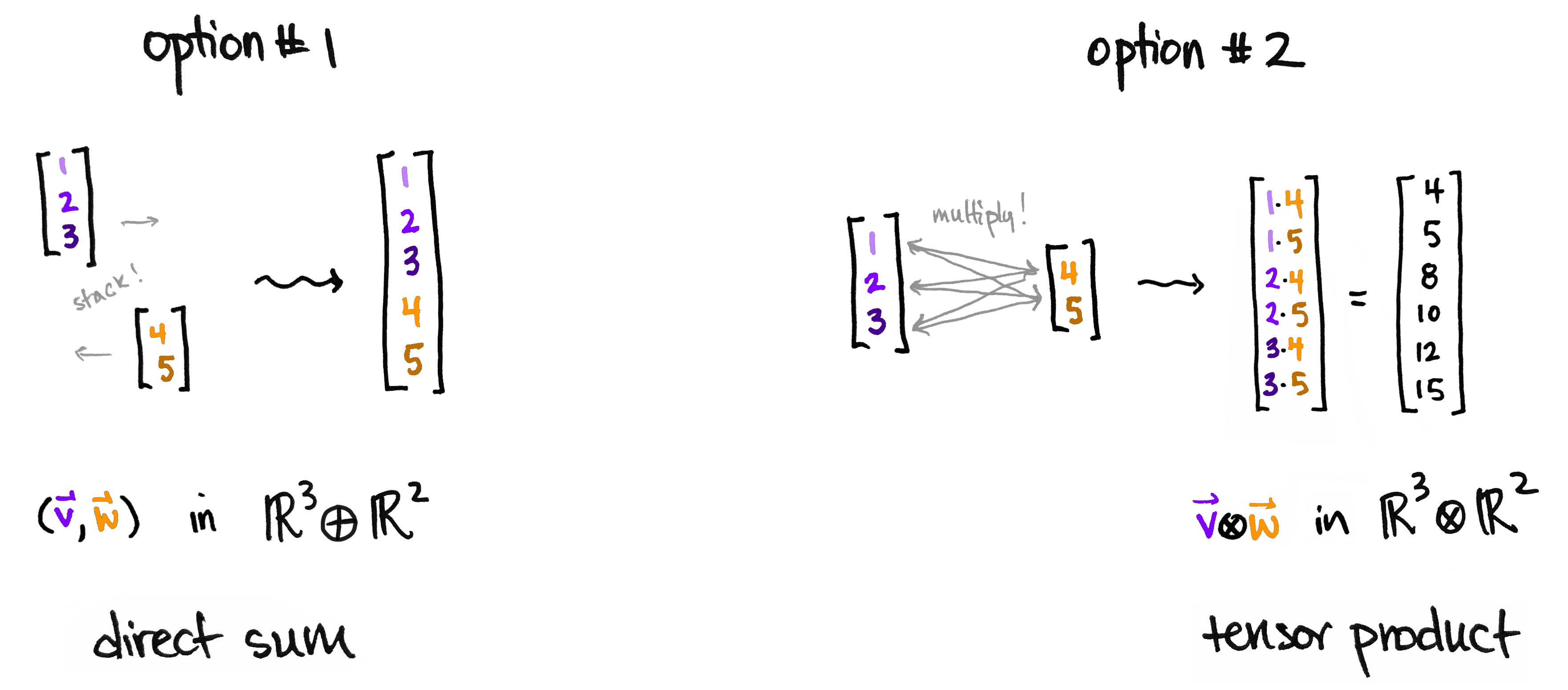
Chatgpt4o를 시켜서 타이핑 노가다를 시켜 다음을 얻는다. 그림은 여기서 얻었다.

1. $e_1 \otimes f_1$:
   $e_1 \otimes f_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \cdot 1 \\ 1 \cdot 0 \\ 1 \cdot 0 \\ 0 \cdot 1 \\ 0 \cdot 0 \\ 0 \cdot 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

2. $e_1 \otimes f_2$:
   $e_1 \otimes f_2 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \cdot 0 \\ 1 \cdot 1 \\ 1 \cdot 0 \\ 0 \cdot 0 \\ 0 \cdot 1 \\ 0 \cdot 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

3. $e_1 \otimes f_3$:
   $e_1 \otimes f_3 = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \cdot 0 \\ 1 \cdot 0 \\ 1 \cdot 1 \\ 0 \cdot 0 \\ 0 \cdot 0 \\ 0 \cdot 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}$

4. $e_2 \otimes f_1$:
   $e_2 \otimes f_1 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \cdot 1 \\ 0 \cdot 0 \\ 0 \cdot 0 \\ 1 \cdot 1 \\ 1 \cdot 0 \\ 1 \cdot 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}$

5. $e_2 \otimes f_2$:
   $e_2 \otimes f_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \cdot 0 \\ 0 \cdot 1 \\ 0 \cdot 0 \\ 1 \cdot 0 \\ 1 \cdot 1 \\ 1 \cdot 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}$

6. $e_2 \otimes f_3$:
   $e_2 \otimes f_3 = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \otimes \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \cdot 0 \\ 0 \cdot 0 \\ 0 \cdot 1 \\ 1 \cdot 0 \\ 1 \cdot 0 \\ 1 \cdot 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}$

독자는 이것이 정규직교기저임을 한눈에 확인할 수 있을 것이다.

---

리스 표현 정리와 수반 변환

먼저, 수반 변환(adjoint transformation), 허미션(Hermitian) (또는 자기수반작용소) 정규 작용소 그리고 유니타리(unitary) 작용소를 정의하자.

수반 변환을 이해하기 전

수반 변환을 이해하기 전에 먼저 리스 표현 정리에 대해서 리뷰할 필요가 있다.

리스 표현 정리 (쉬운 버전) $V$를 유한 차원 복소 내적 공간이라하자. $V^*$의 임의의 원소$\lambda$에 대해서 유일한 원소 $v\in V$가 존재하여 다음이 성립한다.
$\lambda =\left<-,v\right>$. (명확히 말해서, 임의의 $w\in V$에 대해서,
$\lambda(w) = \left<w,v\right>$가 성립함)

$\dagger$
전치 선형 변환을 이야기 할때는 내적이 필요없다. 수반 변환은 반드시 내적이 필요하다. 내적이 꼭 필요한 이유는 여기에 리스표현 정리가 관여하기 때문이다. 리스 표현 정리를 통해서, $v$를 $\lambda$에 대응하는 연산을 $\dagger$라고 하자.
$v^\dagger=\lambda$

벡터를 듀얼에 대응 시킬 수 있음은 자명하나
예를들어서 힐버트 공간 $V=\mathbb{C}^2$에 자연스러운 내적이 주어진 경우,

• 열벡터는 $V$의 원소를
• 행벡터는 $V^*$의 원소를 지칭한다고 할때,

$\begin{pmatrix} x \\ y \end{pmatrix}^\dagger = \begin{pmatrix} \overline{x} & \overline{y} \end{pmatrix}$
이다.

왜 conjugate를 해야할까? 그 이유는, 행렬 곱의 정의와 내적의 정의를 맞추기 위해서 이다.
독자는 $\begin{pmatrix} x \\ y \end{pmatrix}^\dagger \cdot -=\left<-,\begin{pmatrix} x \\ y \end{pmatrix}\right>$를 통해서 위의 대응을 리스 표현 정리와 연결 시킬 수 있다.

위의 대응에서 우리는 행벡터$\begin{pmatrix} x \\ y \end{pmatrix}^\dagger$를 선형범함수$\lambda$로 생각한다. 여기서,
$\lambda =\begin{pmatrix} \overline{x} & \overline{y} \end{pmatrix}$은 열벡터 $v$를 입력받아서, $\begin{pmatrix} \overline{x} & \overline{y} \end{pmatrix}v$를 출력하는 함수이다.

듀얼 벡터를 벡터로 대응 시킴은 자명하지 않으며
리스 표현 정리는 임의의 듀얼벡터에도 $\dagger$를 씌울 수 있음을 말해준다.

리스 표현정리에 따르면, 임의의 원소 $\lambda\in V^*$는 $\lambda =\left<-,v\right>$라 표현이 가능하다. $\lambda$를 $v$로 대응시키는 연산을 $\dagger$이라 적지 않고, (방향이 반대니까 색을 칠해 구분을 하여) $\dagger$라 적자.

1대1대응인것이 이 정리의 극치이다.

그런 점에서 우리는, $\dagger$$\dagger$$:V\to V$와 $\dagger$$\dagger$$:V^*\to V^*$는 항등임을 안다. 예를들어서 자연스러운 내적이 주어진 경우,

$\begin{pmatrix} x \\ y \end{pmatrix}^\dagger = \begin{pmatrix} \overline{x} & \overline{y} \end{pmatrix}$ 그리고 $\begin{pmatrix} \overline{x} & \overline{y} \end{pmatrix}$$^\dagger$$=\begin{pmatrix} x \\ y \end{pmatrix}$이다.

사실, 파란 $\dagger$와 검정$\dagger$를 구별할 필요가 없다는 정서를 전달하고 싶다. 왜냐하면, $V$와 $V^*$는 쌍대적이고, $\dagger$는 단순히 공간에서 그것의 쌍대공간으로 가는 대응이라고 이해하고 있기 때문이다.

더 나아가서, 리스표현정리는
유한차원내적공간에 주어진 $\dagger$가 힐버트공간으로 확장에서 쓸 수 있음을 알려준다.

리스 표현 정리

출처 : https://iseulbee.com/archives/riesz-representation-theorem/

수반 변환이란, 간단히 말해서 연산자에 $\dagger$를 씌우는 것을 의미 한다.

독자는 행렬의 경우 어떻게 $\dagger$를 씌우는지 명확히 알 것이다. 예를 들어, $2 \times 2$ 행렬인 경우:

$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$

의 수반 변환은 다음과 같다:

$A^\dagger = \begin{pmatrix} \overline{a} & \overline{c} \\ \overline{b} & \overline{d} \end{pmatrix}$

주의 : 자연스러운 내적이 주어진 경우일 때만 저렇게 된다!

수반 변환을 이해하면, 허미션 작용소 (Hermitian Operator), 유니타리 작용소 (Unitary Operator)의 정의를 곧바로 이해할 수 있다.

허미션 연산자와 유니타리 연산자 그리고 정규연산자의 정의도 수반 변환을 통해서 얻는다.

허미션 작용소 (Hermitian Operator)

행렬 또는 선형 변환 $A$가 다음 조건을 만족하면 허미션(또는 자기수반) 작용소라고 한다:
$A^\dagger = A$

유니타리 작용소 (Unitary Operator)

행렬 또는 선형 변환 $U$가 다음 조건을 만족하면 유니타리 작용소라고 한다:
$U^\dagger U = U U^\dagger = I$

정규 작용소 (Normal Operator)
행렬 또는 선형 변환 $A$가 다음 조건을 만족하면 정규 작용소라고 한다:
$A^\dagger A= A A^\dagger$

보다 자세한 이야기(예를들어서, 수반변환의 의미 및 정의)는 (스펙트럴 정리)파트에서 다루도록 하겠다.
왜? 정규작용소라는걸 생각하고 저렇게 정의하지? 그것도 다루도록 하겠다.

양자 역학에서의 위치와 운동량

먼저, 1차원 직선 $\mathbb{R}$에서의 위치 $x$와 운동량 $p$를 지닌 입자를 나타내고자 한다. 고전적인 입자는 간섭 및 중첩을 일으키지 않으나, 양자 역학에서 입자는 간섭 및 중첩 현상을 일으킨다. (이것은 오해를 불러일으키는 표현이지만, 달리 다른 표현이 없다.)

생각 정리 : 만약, 파동함수가 복소수값을 가지지 않는다면?
단순히 입자가 확률적으로 존재함을 말하기 위한 것이라면, 파동함수가 아니라 통계학에서 말하는 확률밀도함수여도 충분하다.

따라서, 우리는 $\mathbb{R}$에서 $\mathbb{C}$로 가는 함수 $\phi : \mathbb{R} \to \mathbb{C}$를 사용하여 입자의 상태를 나타낸다. 이 함수 $\phi$는 파동 함수(wave function)라 불리며, 입자의 양자 상태를 기술한다.

위치 연산자

Hall, Quantum Theory for Mathematicians 6.4. 참고

위치 연산자 $X$는 다음과 같이 정의 된다.

$X \psi(x) = x \psi(x)$

여기서 $\phi, \psi$는 $L^2(\mathbb{R})$의 원소이다.

위치 연산자는 고유벡터를 가지지 않는다. 그러나

(엄밀하게 말하면, $X$의 고유벡터는 존재하지 않으나,) 우리는 $\delta(x - \lambda)$가 $X$의 (일반화된) 고유벡터임을 알 수 있다. 이 논의를 엄밀하게 하는것은 매우 복잡하지만, 그 의미는 물리적으로 매우 설득력이 있다.

이 위치 연산자의 (일반화된) 고유벡터 $\delta(x - \lambda)$는 입자가 정확히 위치 $\lambda$에 있는 상태를 뜻한다.

운동량 연산자

Hall, Quantum Theory for Mathematicians 6.6. 참고

운동량 연산자의 정의는 다음과 같다.

$P=-i\hbar \frac{d}{dx}$이다. 정의역을 $L^2(\mathbb{R})$ (절대값 제곱 적분한 것이 정의되는 실수에서 복소수로 가는 함수모임)로 고정하면, 독자는 이것이 허미션임을 쉽게 보일 수 있다.

위치 연산자의 논의와 마찬가지로, 우리는 실제로 고유벡터가 아니지만 고유벡터로서 $e^{ikx}$를 제시할 것이다.

여기서, 내적은 다음과 같이 정의된다.
$\langle f, g \rangle = \int_{-\infty}^{\infty} \overline{g(x)} f(x) \, dx = \langle g | f \rangle$

$e^{ikx}$가 $L^2$의 원소가 아니라는 사실을 무시하면,
다음과 같은 수식을 얻는다. (논리전개는 Hall, 6.6. 참고)

$\langle e^{i\textcolor{red}{k}x}/\sqrt{2\pi}, e^{i\textcolor{red}{l}x}/\sqrt{2\pi} \rangle = \delta(\textcolor{red}{k}-\textcolor{red}{l})$

여기서 빨간 것은 상수이다. 즉, 두 입력 모두 $x$에 대한 함수이다.

그러므로 우리는 $e^{ikx}/\sqrt{2\pi}$를 $L^2$의 orthonormal basis로 간주할 수 있다. 왜냐하면 단순히, 내적 연산수식에 같은 거$k=l$ 넣으면 1되고 다른거 $k\ne l$ 넣으면 0되니까.

이제, $e^{ik_0x}/\sqrt{2\pi}$를 $| k_0\rangle$라 표기하자. 여기서, $k$를 쓰는 이유는 단순히 운동량 연산자 $-i\frac{d}{dx}$를 기준으로 $| k_0\rangle$의 고유값이 $k_0$이기 때문이다.

그리고 $\delta(x-x_0)$를 단순히 $| x_0\rangle$라 표기하자. (표기의 혼동이 심하긴 한데, $k$와 $x$의 모양으로 구분이 되니까) 여기서 $x_0$를 쓰는 이유는, $\delta(x-x_0)$가 위치연산자 $X:= \phi \mapsto x\phi$기준으로 고유값이기 때문이다.

그리고 디렉표기법에서 $\langle -|$은 언제나 linear functinal이다. 이는 리스표현정리를 통해, $| -\rangle$에 대응시키는 방식이라 이해될수 있다.

구체적으로 다음 두 linear functinal을 명확히 이해해야한다.

1. $\langle -, \delta(x-\textcolor{red}{x_0}) \rangle$(Evaluation at $x_0$)

다시말해서, $f\mapsto f(x_0)$. 이것을 디렉델타함수를 활용한 표기로는

$f\mapsto \int f(x)\delta(x-x_0)dx$로 표기한다.

디렉표기법으로는 단순히, $\langle x_0|$으로 표기하자.

예시 : 함수 $f(x) = e^{-x^2}$가 주어졌을 때, $\langle x_0|(f)$는 다음과 같이 계산된다:
$f(x_0) = e^{-x_0^2}$

2. $\langle -, e^{i\textcolor{red}{k_0}x}/\sqrt{2\pi} \rangle$ (푸리에 변환 한 뒤 evaluation at $k_0$)

이것을 디렉표기법으로 단순히 $\langle k_0|$라고 표현하자.

예시 : 함수 $f(x) = e^{-x^2}$가 주어졌을 때, $\langle k_0|(f)$는 다음과 같이 계산된다:
$\langle k_0|(f) = \hat{f}(k_0) = \int \frac{1}{\sqrt{2\pi}}e^{-x^2}e^{-ik_0x}dx$

이제 상당히 설득력 있는 논리 전개를 읽으면, 왜 $\frac{1}{\sqrt{2\pi}}e^{ikx}$를 $L^2(\mathbb{R})$의 orthonormal basis간주하는것이 유용한지를 독자가 이해할 것이라 생각한다. 그리고 (표기가 모호함에도 불구하고) $\langle x_0|$와 $\langle k_0|$가 무엇인지 명확히 이해하게 되리라 생각한다. (읽고 왔다는 전제하에 다음 이야기를 하겠다.)

이제, 우리는 양자역학에서 말하는 푸리에 변환을 이해할 준비가 되었다.

Hilbert space로 충분한가?

사실 양자역학(슈뢰딩거방정식)에서 말하는 양자 상태 모임은 사실 $L^2$보다 더 큰 공간이어야한다. 그렇다면, 진정한 의미의 파동함수들의 공간은 무엇인가? 혹자는 이것을 Rigged Hilbert Space라 부른다. (이것의 엄밀한 fomulation에는 나는 그닥 관심이 없어서 대강 설명하겠다.), 위치와 운동량(Unbounded operator)에 대해서 Spectral theorm을 전개하는것이 가능하므로, 굳이 그 fomulation을 알아야만 할 이유는 없다.

이런 논의(why spectral theory instead of rigged Hilbert spaces?)는 여기서 찾아볼 수 있다.

임의의 linear functional $\in L^{2*}$은 $\langle -, f \rangle$ 꼴로 표현될 수 있으며, 이러한 $f\in L^2$는 유일하게 존재한다. 이를 리스 표현 정리(Riesz Representation Theorem)이라 부른다. 단, 방금 리스 표현 정리를 $f$가 $L^2$인 경우에 한정하였지만, 양자역학을 공부할 적에는 매우 중요한 두 linear functional을 포괄하기 위해서 $L^2$ 제한을 버리고 과감히 사고하는 것이 중요하다. 물론 수학적으로 굉장히 불편한 짓거리이다. 이 불편함의 해소의 열쇠는 리스 표현 정리를 확장함으로서 가능하다. 매우 중요한 두 linear functional을 포함하는 (그러나 리스 표현정리가 성립하는) 공간으로서 얻어낸 것이 Rigged Hilbert Space이다.

여튼 양자역학의 입장에서는 선형범함수가 물리적 의미를 가진다.

예를들어서,

1. 선형범함수 $f\mapsto f(x_0)$의 의미는 $x_0$에 위치하는 상태를 뜻하고, 디렉델타함수에 대응한다.

다시말해서, $f\mapsto \langle f, \delta(x-\textcolor{red}{x_0}) \rangle$의 두번째 입력에 디렉델타함수가 들어간다.

2. 선형범함수 $f\mapsto \hat{f}(k_0)$의 의미는 $\hbar k_0$라는 운동량을 갖는 상태를 뜻한다. (드브로이 관계)

다시말해서, $f\mapsto \langle f, e^{i\textcolor{red}{k_0}x}/\sqrt{2\pi} \rangle$\

3. 물론, 1,2에 대응하는 디렉델타 함수와 $\frac{1}{\sqrt{2\pi}}e^{+ik_0x}$도 동일한 의미를 가진다.

푸리에 변환은 Unitary하다!

스펙트럴 정리의 핵심 키워드는 Unitary 대각화가능이다. 그리고 이 핵심 키워드에 가장 걸맞는 푸리에 변환사이드의 내용은 다음과 같다.

Plancherel Theorem
임의의 $f,g\in L^2(\mathbb{R})$에 대해서, $\left<\hat{f},\hat{g}\right>= \left<f,g\right>$

---

다음을 확인해보자

$K:=-i\frac{d}{dx}$라 정의하자. 그리고 $\hat{\psi}(k)=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\psi(x) e^{-ikx}dx$이라 하자. 그러면, $\widehat{[K\psi]}(p)=k\hat{\psi}(p)$ 이 성립하는가?

독자는 이것이 항상 성립하지는 않음을 쉽게 눈치 챌 수 있을 것이다. 그러나 이것이 그냥 성립한다고 대강 생각하는 편도 괜찮다.

귀찮은 사람은 엄밀함을 희생해서 다음과 같이 적을 수 있을 것이다.

---

"nice enough"한 함수 $\psi$에 대해,
$\hat{\psi}(k)=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}\psi(x) e^{-ikx}dx$

---

마찬가지로, 우리는 푸리에 변환을 살짝 바꾸어서

"nice enough"한 함수 $\psi$에 대해,:
$\widetilde{P\psi} = p\tilde{\psi}(p)$

이 되도록 다음과 같이 $\tilde{\psi}$를 정의할 것이다.

$\tilde{\psi}(p) = \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-ipx/\hbar} \psi(x) \, dx$

이제 Hall, Quantum Theory for Mathematicians 6.6.을 읽어보자. 아래는 요약.

이제, 양자역학에서 푸리에 변환의 의미를 살펴보자. 이 내용은 책내용을 그대로 (줄여서) 옮겨놓은 것으로 더 자세한 내용이 필요하면 책을 보면 되겠다.

양자역학에서의 푸리에 변환의 의미

운동량 연산자 $P$는 다음과 같이 정의된다:

$P\psi(x) = -i\hbar \frac{d\psi(x)}{dx}$

질문 다음을 만족시키는 유니타리 변환$U:\psi \mapsto \tilde{\psi}$가 존재하는가?

• $U[P\psi](p)=p[U\psi](p)$
  존재한다면, $U$의 정의역은 어떻게 될까?

"nice enough"한 함수 $\psi$에 대해, 다음이 성립한다:
$\widetilde{P\psi} = p\tilde{\psi}(p)$

이 방정식은 유니터리 변환 $\psi \rightarrow \tilde{\psi}$가 운동량 연산자 $P$를 $p$로의 곱셈으로 변환함을 의미한다. 즉, 스펙트럴 정리가 "곱셈 연산자" 형태로 푸리에 변환에 의해 달성된다는 것을 나타낸다.

이 정의는 다음과 같은 맥락에서 이해할 수 있다:
1. 푸리에 변환을 통해 위치 공간에서의 파동 함수를 운동량 공간으로 변환한다.
2. 운동량 공간에서의 연산자는 단순히 $p$와의 곱셈으로 표현된다.
3. 이는 다시 위치 공간에서의 미분 연산자로 대응된다.

따라서, 운동량 연산자는 위치 공간에서의 미분 연산자의 허미션 형태로 정의되며, 이는 푸리에 변환과 스펙트럴 정리를 통해 정확히 이해할 수 있다.

푸리에 변환의 유용성

운동량 분포 계산

파동 함수 $\psi(x) = e^{-x^2/2}$의 운동량 분포를 구해보자. 이는 주어진 위치 공간에서의 파동 함수를 운동량 공간으로 변환하는 푸리에 변환을 통해 얻을 수 있다.

1. 푸리에 변환 정의:
   파동 함수 $\psi(x)$의 푸리에 변환 $\tilde{\psi}(p)$는 다음과 같이 정의된다:
   $\tilde{\psi}(p) = \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-ipx/\hbar} \psi(x) \, dx$

   이 푸리에변환 정의$U(\psi):=\tilde\psi$가 다음을 만족시키는지 확인하고 넘어가자. 여기서, $P=-i\hbar\frac{d}{dx}$

   • $U[P\psi](p)=p[U\psi](p)$

2. 파동 함수 대입:
   주어진 파동 함수 $\psi(x) = e^{-x^2/2}$를 푸리에 변환 정의에 대입하자:
   $\tilde{\psi}(p) = \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-ipx/\hbar} e^{-x^2/2} \, dx$

3. 적분 계산:
   이 적분을 계산하기 위해, 적분의 상수를 분리하여 다음과 같이 표현할 수 있다:
   $\tilde{\psi}(p) = \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-(\frac{x^2}{2} + \frac{ipx}{\hbar})} \, dx$

   이를 좀 더 간단히 하기 위해, 지수 부분을 완성 제곱법을 사용하여 정리할 수 있다:
   $\tilde{\psi}(p) = \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-\frac{1}{2}(x^2 + \frac{2ipx}{\hbar})} \, dx$
   $= \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-\frac{1}{2}(x^2 + \frac{2ipx}{\hbar} + \frac{p^2}{\hbar^2})} e^{-\frac{p^2}{2\hbar^2}} \, dx$

   여기서 $e^{-\frac{p^2}{2\hbar^2}}$는 적분과 무관한 상수이므로 적분 밖으로 빼낼 수 있다:
   $\tilde{\psi}(p) = e^{-\frac{p^2}{2\hbar^2}} \cdot \frac{1}{\sqrt{2\pi \hbar}} \int_{-\infty}^{\infty} e^{-\frac{1}{2}(x + \frac{ip}{\hbar})^2} \, dx$

   이제, 변수를 $u = x + \frac{ip}{\hbar}$로 치환하면 적분의 범위는 변하지 않으며, 적분 결과는 다음과 같다:
   $\tilde{\psi}(p) = e^{-\frac{p^2}{2\hbar^2}} \cdot \frac{1}{\sqrt{2\pi \hbar}} \cdot \sqrt{2\pi}$

4. 결과:
   최종적으로, $\tilde{\psi}(p)$는 다음과 같이 계산된다:
   $\tilde{\psi}(p) = \sqrt{\frac{\hbar}{2\pi}} e^{-\frac{p^2}{2\hbar^2}}$

이는 $\psi(x) = e^{-x^2/2}$에 대한 푸리에 변환 결과로서, $\tilde{\psi}(p)$는 운동량 공간에서의 가우시안 형태의 파동 함수임을 나타낸다. 이는 $\psi(x)$가 위치 공간에서 가우시안 함수일 때, $\tilde{\psi}(p)$도 운동량 공간에서 가우시안 함수가 됨을 보여준다.

Global phase 이해하기

푸리에 변환은 양자 상태를 이해하는 데 큰 도움을 준다. 예를 들어, Global phase가 양자 상태에 작용하는 방식을 푸리에 변환을 통해 명확하게 이해할 수 있다.

Global phase

임의의 파동 함수 $\phi$에 대해 $e^{i\theta}\phi$ (여기서 $\theta$는 실수)는 물리적으로 완전히 동일하다. 이를 이해하는 것은 (더 추상적인 세팅에서의) pure state를 이해하는 데 핵심이다.

전체 공간에 동일한 위상변환을 생각한다는 의미에서, 이런 것을 말할때는 global phase라는 용어를 사용한다.

예를들어서, 파동함수의 경우 위상 변화가 물리적인 위치와 운동량 분포에 영향을 미치지 않으며, 아래에서 명확하게 보이도록 하겠다.

위치 관점에서의 동일성

굳이 계산안해도 당연하다.

파동 함수의 절대값, $|\phi(x)|^2$,는 입자가 특정 위치 $x$에 존재할 확률 밀도를 나타낸다. $e^{i\theta}\phi$의 경우, $|e^{i\theta}\phi(x)|^2 = |e^{i\theta}|^2 |\phi(x)|^2 = |\phi(x)|^2$이므로, 위상 $\theta$가 위치 확률 분포에 영향을 주지 않는다. 이는 직관적으로 와닿는다.

운동량 관점에서의 동일성

운동량 관점에서의 $\tilde{\phi}$와 $e^{i\theta}\tilde{\phi}$의 동일성을 고려하면 당연하다.

운동량 공간에서 파동 함수의 위상 변화는 파동 함수의 푸리에 변환에서의 변화를 야기한다. 그러나 이 변화는 물리적 측정값에 영향을 주지 않는다. 이를 수학적으로 설명해보면:

1. 파동 함수 $\phi(x)$의 푸리에 변환을 $\tilde{\phi}(k)$라 하자.
2. $\phi(x)$에 위상 $e^{i\theta}$를 곱한 함수 $\psi(x) = e^{i\theta}\phi(x)$의 푸리에 변환은 $\tilde{\psi}(k) = \int e^{-ikx} \psi(x) \, dx = \int e^{-ikx} e^{i\theta} \phi(x) \, dx = e^{i\theta} \tilde{\phi}(k)$가 된다.

푸리에 변환의 결과가 단순히 $e^{i\theta}$만큼 곱해진 형태이므로, 운동량 분포 $|\tilde{\psi}(k)|^2 = |e^{i\theta} \tilde{\phi}(k)|^2 = |\tilde{\phi}(k)|^2$도 동일하게 유지된다. (푸리에 변환의 선형성이다.)

이와 같이, 파동 함수의 위상은 위치와 운동량 분포에 영향을 주지 않으며, 두 함수는 물리적으로 동일한 상태를 나타낸다.

운동량의 의미

직관적으로 말해서
운동량 연산자는 허미션화 시킨 공간 미분연산자에 불과하다.
에너지 연산자는 허미션화 시킨 시간 미분연산자에 불과하다.
왜 이런 방식으로 생각하는가?
Noether의 정리에 따르면, 각 대칭성은 보존 법칙에 대응하고, 보존 법칙에 맞는 물리량이 존재한다. 운동량 연산자는 공간 이동 연산자x의 생성자(generartor)로 간주될 수 있다. 이 의미는 공간 이동에 따라 불변하는 물리량으로서 운동량을 정의하겠다는 것이다. 마찬가지로 시간 이동에 대응하는 대칭성은 에너지 보존 법칙에 대응한다. 시간 이동 연산자의 생성자는 해밀토니안(에너지 연산자)이다. 이는 시간 이동에 따라 불변하는 물리량으로서 에너지를 정의하겠다는 것이다.

대칭성과 보존 법칙의 대응

• 공간 이동 대칭성: 물리 법칙은 위치에 관계없이 동일하다.
  보존 법칙: 운동량 보존
• 시간 이동 대칭성: 물리 법칙은 시간에 관계없이 동일하다.
  보존 법칙: 에너지 보존

그러나 이런 설명만 봐서는 미분이랑 이동(translattion) 대칭이 뭔 상관인지 도무지 이해할 수 없다. 내가 이 부분에 있어서 이해를 얻는데 (간접적으로) 도움이 된 자료를 소개하고, 간단히 논리를 전달하고자 한다.

Why is momentum the generator of translations?

Momentum as a Generator of Translation

사실 운동량이 generator of translation이라는 것은 어디서든 쉽게 설명을 찾을 수 있다. 원한다면 Lie group과 Lie algebra를 활용한 엄밀한 설명을 찾아보는 것도 가능하다. 그리고 이런 정의가 (운동량을 mv로 정의하는 고전적 정의보다) 훨씬 근본적이고 확장성을 갖는다는 것도 설득력이 있다. 예를 들어 canonical transformations을 활용한 양자화(물리량을 연산자로 바꾸는 행위)가 입자물리학에서 성공을 거둔 것도 이러한 사고 방식이 더 근본적임을 설득할 근거가 된다. 그러나 이런 내용들을 살펴보는 것만으로는 해소할 수 없는 불편함이 있다. 사실 진짜 불편한 것은 도대체 왜 generator of translation 생각하느냐?라는 의문을 지울 수 없다는 것이다. (동의하는가?)

이 불편함을 당장을 해결하지 않고 (나의 이해 수준으로는 해결 불가능하다) 대략적인 스토리를 정리해보자.

• 먼저, 양자역학은 고전역학으로 근사되어야한다. (이견이 없을 거라 생각함) 다시 말해서, 운동량 연산자가 고전적 운동량으로 대응되는 방식으로 정의되어야 한다.

• 이 맥락에서 Poisson bracket과 commutator가 자연스럽게 소개 된다.

  canonical quantization - first quantization 참고

구체적으로 고전역학에서 포아송 괄호는 두 물리량
$f$와 $g$에 대해 다음과 같이 정의된다:

$\{f, g\} = \frac{\partial f}{\partial q} \frac{\partial g}{\partial p} - \frac{\partial f}{\partial p} \frac{\partial g}{\partial q}$

$f,g$에 각각 $q$와 $p$를 대입하면 1이된다.

이걸 양자화의 맥락에서 다시 말하자면, 운동량을 $\{q, g\}=1$를 만족시키는 $g$로 정의하자는 것이다. 물론, Why is momentum the generator of translations?에서 말하듯 이것은 유일하게 정의되지는 않는다.

양자역학에서는 이 포아송 괄호의 양자적 대응으로서 연산자 사이의 교환 관계가 도입된다.
$[\hat{x}, \hat{p}] = i\hbar$

---

출처 : 실체에 이르는 길 (로저 펜로즈)

예를 들어, 다음과 같은 미분 방정식을 푼다고 하자:
$\left(1+\frac{d^5}{dx^5}\right) y= x$
이때 우리는 $\frac{d}{dx}$를 $D$로 정의하고 숫자를 다루듯이 취급하며 문제를 해결할 수 있다.

즉, 양변에 $(1+D^2)^{-1}$을 곱하는 방식으로:
$y=(1-D^2+D^4-D^6+\cdots)x^5$
$=x^5-20x^3+120x$
해를 구할 수 있다.

비록 $D = \frac{d}{dx}$라는 양을 대수적으로 일반적인 숫자처럼 취급할 수 있지만, $D$와 $x$가 섞여 있을 때는 주의해야 한다. 왜냐하면 이들은 교환하지 않기 때문이다. 우리는 $x$와 $D$를 어떤 보이지 않는 함수 $C(x)$에 작용하는 연산자로 생각해야 한다. 연산자 $x$는 그 오른쪽에 있는 항에 단순히 $x$를 곱하고, $D$는 그 오른쪽에 있는 항을 $x$에 대해 미분한다. 그 결과, 다음과 같은 교환 관계를 얻는다:
$[x, D] = Dx -xD=1$

예를들어서, $[x, D](1) = \frac{d}{dx}(x\cdot 1) - x \frac{d}{dx}(1) = 1-x0=1$이다. $1$말고 임의의 test function $C(x)$에 대해서도 $1$이 나온다.

이 관계는 양자역학에서 매우 중요한 역할을 한다. 이것은 양자역학에서 다음과 같이 번역된다. 위치연산자 $\hat{x}$와 운동량 연산자 $\hat{p}$는 다음과 같은 교환 관계를 가진다.
$[\hat{x}, \hat{p}] = i\hbar$

---

• 이 이야기를 완성시키기 위해서, 고전역학(헤밀톤 역학)을 살펴볼 필요가 있다. 이는 나름대로 정리한 내 글의 링크이다.

스펙트럴 정리와 확률 해석

양자역학 이론이 고유값 및 고유 벡터가 물리적 의미를 지니도록 구성되어 있다. 그리고 물리적 관측 가능량(observables)은 허미션 연산자(self-adjoint operators)로 표현되고, 관측 값은 고유값으로 표현되며, 물리적 상태(정확히는 이들의 superposition)는 고유 벡터로 표현된다는 것을 기억하자.

양자 역학에서 스펙트럴 정리가 필수인 이유는
스팩트럴 정리가 허미션 연산자를 연산 가능한 물리량(실수)로 취급하게 하기 때문이다. 조금 더 명확히 말해서, 어떤 함수 $f:\mathbb{R} \to \mathbb{C}$와 허미션 연산자 $A:H_\to H$에 대해서, $f(A):H \to H$ 따위를 명확하게 정의 할 수 있도록 해주기 때문이다. (이를 functional calculus라 한다.) 그리고 이런 것이 명확하게 정의되는 맥락안에서, 고전역학에서 실수인 물리량을 연산자인 물리량으로 치환함으로서, 고전역학을 양자화시키는 것이 정당화된다.

Note : 예를 들어서, $\sigma(A)=\{\lambda_1,\ldots,\lambda_n\}$인 경우 위의 식에서의 적분은 단순히 덧셈이 되고 식은 다음과 같이 단순해 진다.

$f(A) = \sum_{i=1}^n f(\lambda_i)\mu^A(\lambda_i)$, 여기서 $\mu^A(\lambda_i)$는 단순히 $\lambda_i$에 대응하는 고유공간으로의 orthogonal projection이다.

예를 들어서 고전 역학의 $E=p^2/(2m)+V(x)$이라는 식을 생각해보자. 여기서, $E, p,x$는 실수이다. 이 실수 대신에 연산자를 대입한 것이 슈뢰딩거 방정식이다. 즉, 슈뢰딩거 방정식은 스팩트럴 정리로부터 나오는 functional calculus를 고전역학에 적용하여 얻은 것이다.

---

예시: 고전역학에서 양자역학으로의 전환 슈뢰딩거 방정식

고전역학의 에너지 식 $E = \frac{p^2}{2m} + V(x)$에서 $E, p, x$는 모두 실수다. 이를 연산자로 대체하면 다음과 같이 된다:

• 위치 연산자 $\hat{x}$
• 운동량 연산자 $\hat{p} = -i \hbar \frac{d}{dx}$
• 에너지 연산자 $\hat{E}=i \hbar \frac{\partial}{\partial t}$

이를 통해 슈뢰딩거 방정식이 도출된다:
$\hat{E} \psi = \left( \frac{\hat{p}^2}{2m} + V(\hat{x}) \right) \psi = E \psi$

이처럼, 스펙트럴 정리(로부터 도출되는 functional calculus)를 통해 고전역학의 실수 물리량을 양자역학의 연산자로 바꾸는 것이 정당화된다.

---

양자역학에서 스펙트럴 정리가 중요한 두번째 이유는

스펙트럴 정리가 허미션 연산자 $A$를 확률 변수처럼 다룰 수 있게 하기 때문이다.

---

불연속적인 스펙트럼의 경우만을 설명

불연속적인 스펙트럼을 가진 허미션 연산자의 경우, 고유값은 분리된 값들로 이루어져 있다. 이때 각 고유값에 대한 확률을 계산하는 과정은 다음과 같다.

1. 고유값과 고유 벡터: 허미션 연산자 $A$가 고유값 $\lambda_j$와 대응하는 고유 벡터 $e_j$를 가진다고 하자. 상태 (\psi)를 고유 벡터의 선형 결합으로 나타낼 수 있다.
   $\psi = \sum_j c_j e_j$

2. 확률 계산: 상태 $\psi$에서 고유값 $\lambda_j$가 관측될 확률은 다음과 같다.
   $\text{prob}_{\psi}(A = \lambda_j) = |c_j|^2$

연속적인 스펙트럼의 경우만을 설명

연속적인 스펙트럼을 가진 허미션 연산자의 경우, 확률을 계산하는 과정은 다음과 같다.

1. 스펙트럼 측도: 연산자 $A$의 스펙트럼을 나타내는 연속적인 고유값 집합 $E$에 대해, 측도 $P_E$를 정의한다. 이는 $E$에 해당하는 스펙트럼 부분 공간으로의 투영 연산자이다.

2. 확률 계산: 주어진 상태 $\psi$에서 $A$가 구간 $E$에 속할 확률은 다음과 같다.
   $\text{prob}_{\psi}(A \in E) = \langle \psi, P_E \psi \rangle$

여기서 $P_E$는 구간 $E$에 대한 스펙트럴 프로젝터이며, 상태 $\psi$를 구간 $E$에 해당하는 부분 공간으로 투영한다. 예를 들어, 상태 $\psi$가 특정 함수 $f(x)$로 주어졌을 때, 위치가 구간 $E = [a, b]$에 있을 확률은 다음과 같다.
$\text{prob}_{\psi}(X \in [a, b]) = \int_a^b |f(x)|^2 \, dx$

---

수리적으로는 $A$를 확률변수로 취급하는 것이 $A$의 spectrum( 고유값들의 집합이라 보면 된다.)에 측도(measure)가 (다음을 만족하는 것이) 존재함으로서 타당해진다.

그리고 더 나아가서, 임의의 측도공간 $X$에 대해서도 이 논의를 확장할 수 있다.

Note : 만약 $A$가 불연속 스펙트럼을 갖는 경우, 스펙트럼의 부분 집합 $E=\{\lambda_1,\ldots,\lambda_n\}$에 대해서, $\mu(E)=\Sigma_{i=1}^n \mu^A(\lambda_i)$가 된다. 여기서, $\mu^A(\lambda_i)$는 $\lambda_i$에 대응하는 고유공간으로의 orthognal projection이다.

사실 정말로 전달하고 싶었던 것은, Spectral theory는 실수 확률변수를 허미션 연산자에 대응을 시켜준다는 것이었다. 즉, 임의의 복소 확률 변수 $f$에 대응하는 ($A$의 스펙트럴분해와 관련되어 정의되는) 유일한 operator의 존재를 대응시켜주며, 여기서 복소 대신 실확률변수라는 조건을 걸면, 허미션 연산자로 대응이 된다.

1. Constant function on $E$는 orthogonal projection $\mu(E)$에 대응됨.
2. 연산자 $\int_X f d\mu$는 bounded임. 구체적으로,
   $\|\int_X f d\mu\| \le \|f\|_1$
3. 두 r.v. $f,g$의 곱에 대응하는 연산자는 각각에 대응하는 연산자의 곱임. -> 따라서, 그들은 서로 교환 가능함.
   $\int_X fg d\mu=\left(\int_X fd\mu\right)\left(\int_X g d\mu\right)$
4. 만약, $f$가 real valued이면, 그것에 대응하는 연산자는 허미션임.
   $\int_X \overline{f}d\mu=\left(\int_X fd\mu\right)^\dagger$

여기에 대한 내 생각
위의 논의는 생각보다 훨씬 복잡하고, 슬프게도 기초적인 예시에 적용하여 이해도를 높이는 것 조차 마음대로 안된다. (예를 들어서, 위치 운동량 연산자는 unbounded라서 위에서 소개한 정리들에 적용이 안된다.) 그러나 (많은 사람들이) 스펙트럴 정리를 양자역학의 수학화의 핵심으로 여기는 부분은 설득이 되었다.

양자역학에 따르면 관측 가능량이 근본적으로 확률론적인 성질을 가져야만 하기 때문에, (스팩트럼을 공역으로 갖는 확률 변수로서 해석이 가능한) 허미션 연산자가 관측 가능량이어야 함은 상당히 설득력 있다. 그러나 이것만으로는 설득력이 부족하다.

spectral theory가 복잡하다는 이유로 확률론적인 논거만으로 양자역학을 만든다고 해보자. 이럼 안되는 이유가 무엇인가?

내 생각에 그 이유를 보여주는 강력한 예시는 불확정성 원리이다. 단순 확률 변수는 교환이 언제나 가능하지만 허미션 연산자는 그렇지 않은 것이, (허미션 연산자 기반의) 양자역학이 불확정성 원리를 다룰 수 있는 공간을 제공해준다.

---

확률 변수의 곱이 비가환이게 확률론을 만들고, 이를 양자역학의 토대를 마련하는데 이용하자?

이런 생각까지 들었다면, 아래 글을 읽어보기를 추천한다.

https://terrytao.wordpress.com/tag/noncommutative-probability/

---

스펙트럴 정리와 양자역학

양자 민수야, 이건 네가 좋아하는 곰인형이야. 이제 이 곰인형의 그림자를 한번 봐볼까? 만약에 불빛이 위에서 곰인형을 비추면, 곰인형의 그림자는 바닥에 생기겠지? 이때 이 그림자는 곰인형의 모양을 따라가지만, 높이는 전혀 보이지 않아. 이처럼 물체가 그림자로 바닥에 딱 붙어 있는 모양을 '정사영'이라고 해. 여러 가지 모양의 그림자를 만들 수 있을 거야. 그리고 여러 가지 그림자를 만들어서 그림자만 잘 관찰하는 것도 하나의 재미있는 일 일거야. 마치 블록을 여러 개로 나눠서 각각의 블록을 따로따로 본 다음에, 이 블록들을 다시 합쳐서 원래 모양을 만드는 것처럼, 이렇게 여러 가지 그림자들을 통해서, 원래 곰인형의 모양을 알 수 있을 거야. - chatgpt에게 유치원생에게 정사영(양자역학 관점에서) 설명하기 요청 결과. (양자 민수만 본인이 적음.)

스펙트럴 정리의 핵심 키워드는 정사영(Orthogonal Projection)이다. 양자역학에서 정사영이란 측정과 완전히 같은 것이다. 구체적으로 말해서 스펙트럴 정리가 시사하는 바는 다음과 같다. 코펜하겐 해석에 따르면 어떤 양자 상태를 측정하면, 그 상태는 특정한 고유벡터(측정된 값에 대응하는 상태)로 '붕괴'(collapse)한다. 이 붕괴과정은 사실상 그 상태를 해당 고유벡터 방향으로 정사영하는 것과 동일하다. 그리고 양자역학에서 물리량이란 그 물리량에 대응하는 허미션 연산자(operator)로 나타난다. (허미션 연산자란 조건이 매우 중요하다.) 그리고 그 연산자는 (스펙트럴 정리에 의해서) 언제나 스펙트럴 분해가 가능하다. 물리량의 스펙트럴 분해란, 비유하자면 물리량을 정사영의 합으로 표현하는 것을 의미한다.

---

스펙트럴 정리

다양한 맥락에서 스펙트럴 정리를 재정의할 수 있지만, 이해를 위해서는 이것 하나면 족하다.

직교행렬을 이용해서 대각화 가능 행렬은 대칭행렬이다. 그리고 대칭 행렬은 항상 직교행렬을 이용해 대각행렬로 변환할 수 있다.

대칭이 아니면 직교 대각화 안된다.

다음과 같은 행렬 $A$를 보자:

$A = \begin{pmatrix} 4 & 1 \\ 2 & 3 \end{pmatrix}$

1. 고유값 계산:

고유값은 $\lambda_1 = 5$와 $\lambda_2 = 2$이다.

2. 고유벡터 계산:

각 고유값에 대응하는 고유벡터를 구한다.

• $\lambda_1 = 5$일 때:

고유벡터는 $\mathbf{v}_1 = \begin{pmatrix} 1 \\ 1 \end{pmatrix}$이다.

• $\lambda_2 = 2$일 때:

고유벡터는$\mathbf{v}_2 = \begin{pmatrix} 1 \\ -2 \end{pmatrix}$이다.

3. 서로 다른 고유값에 해당하는 고유벡터가 직교일 수 없으므로, $A$는 직교대각화가 불가능하다.

필자가 생각할 때, 스펙트럴 분해 계산과정에서 가장 신기한 부분은 대칭 행렬의 서로 다른 고유값에 대응하는 고유벡터들이 항상 직교한다는 사실이다. 그리고 그 사실은 대칭행렬을 Self Adjoint matrix로 재정의하는 동기가 된다.

---

Fact

실수성분의 대칭행렬 $A$의 고유벡터 $v, w$에 대해서, 대응하는 두 고유값이 서로 다르면, 다음이 성립한다.
$v'w=0.$

Proof

Spectral 정리에 의해서, 바로 증명된다. 다른 증명방법을 소개한다. $v, w$에 대응하는 고유값이 각각 $\lambda_v, \lambda_w$라 하자. 그러면,

$\lambda_v v'w = (Av)'w$

$= v'A'w$

$= v'\lambda_w w$

$= \lambda_w v'w.$

따라서,

$(\lambda_v - \lambda_w) v'w = 0$이다.

---

위 증명을 잘 관찰 해보면

$(Av)$의 전치$(Av)^\top$가 $v^\top A^\top$으로 적힌다는 것이 키 포인트이다. 이 증명에 대한 관찰을 응용하여, 우리는 대칭행렬을 다음과 같이 재 정의할 수 있다.

힐베르트 공간 $V$에서 선형 연산자 $H$가 모든 $x, y \in V$에 대해 다음 조건을 만족하면, $H$를 허미션 연산자(또는 자기 수반 연산자)라고 한다.:

$\langle Hx, y \rangle = \langle x, Hy \rangle$

---

위 정의를 대칭행렬과 더욱더 연결시키고 싶으면 Adjoint Operator의 정의를 자세히 관찰하기를 바란다.

Adjoint Operator
힐베르트 공간 $V, W$에 대해서 선형 변환 $T: V \to W$의 Adjoint Operator란 다음을 만족시키는 연산자 $T^*: W \to V$이다.

모든 $x \in V, y \in W$에 대해서
$\langle Tx, y \rangle = \langle x, T^* y \rangle$

위 정의가 잘 동작함을 이해하기

두 가지 이해 방식이 있다. 첫 번째는 리스 표현 정리를 통해서 저러한 연산자 $T^*$의 존재성과 유일성을 받아들이는 것이다. 두 번째는, 직접 다음과 같이 구성하는 것이다. 두 이해 방식 모두 매우 중요하다. 두 번째 이해 방식은 첫 번째보다 조금 기술이 복잡하지만, self adjoint operator를 대칭 행렬의 일반화로 이해하게 하는 측면이 있다. (그리고 잘 살펴보면 두 번째 방식 또한 리스 표현 정리를 요구한다.)

1. 전치 연산자 정의하기

$T: V \to W$의 전치 연산자 $T^t: W^* \to V^*$, 다음과 같이 정의된다.

$[T^t(g)](x) = g(T(x)) \quad \text{for all } x \in V, y \in W$

2. 데거($\dagger$) 정의하기. 단순히 $\dagger$라고 하자.

   단순히 transpose and complex conjugate의 추상화이다.

• 임의의 힐베르트 공간 $V$에 대해서 $\dagger: V \to V^*$는 다음과 같이 정의된다.

$\dagger : v \mapsto \langle \cdot, v \rangle$

• 임의의 힐베르트 공간 $V$에 대해서 $\dagger: V^* \to V$는 다음과 같이 정의된다.
  $\dagger : \lambda \mapsto v$ where $v$ is the unique vector in $V$ such that
  $\lambda = \langle \cdot, v \rangle$. (존재성 및 유일성은 리스 표현 정리가 보장함.)

3. 다음을 $T$의 수반 변환이라 정의하자.

   $T^* = \dagger \circ T^t \circ \dagger$

   이 과정을 더 명확히 적으면 다음과 같다.:

   $T^* : W \xrightarrow{\dagger} W^* \xrightarrow{T^t} V^* \xrightarrow{\dagger} V$

   ---

정규 연산자 이해하기

선형대수학을 심화하여 학습한 독자는 정규 연산자(normal operator)를 들어보았을 것이다. 정규 연산자에 대한 가장 쉬운 설명은 다음과 같으나, 심각한 비판점이 있으니 잘 살펴보길 바란다.

쉬운 설명

• 실수(real numbers)는 자기 수반 연산자(self-adjoint operators)와 같다.
• 음이 아닌 실수(nonnegative real numbers)는 양의 연산자(positive operators)와 같다.
• 단위원 위의 복소수(complex numbers on the unit circle)는 유니터리 연산자(unitary operators)와 같다.

정규 연산자는 복소수에 비유할 수 있다. 복소수에는 실수, 양의 실수, 단위원 위의 복소수가 포함되며, 이는 각각 자기 수반 연산자, 양의 연산자, 유니터리 연산자에 대응한다. 마찬가지로 자기수반연산자 양의 연산자 그리고 유니타리 연산자 모두 정규연산자이다.

위의 비유를 이해하기 위해서는 연산자의 고유값들을 실제로 구해보면 된다. 예를들어서, 자기수반연산자의 경우 고유값이 모두 실수라서 실수에 비유 되는 것이다.

정규 연산자 제대로 이해하기

정규 연산자는 다음과 같이 정의된다:

정규 연산자 (Normal Operator) 정의
힐베르트 공간 $H$에서 선형 연산자 $T: H \to H$가 다음 조건을 만족하면 정규 연산자라고 한다:

$TT^* = T^*T$

여기서 $T^*$는 $T$의 수반 연산자(adjoint operator)이다.

스펙트럴 정리
스펙트럴 정리에 따르면, 정규 연산자는 고유벡터의 정규 직교 기저를 사용하여 대각화될 수 있다. 즉, 정규 연산자 $T$는 유니터리 연산자 $U$에 의해 다음과 같이 대각화될 수 있다:

$T = U \Lambda U^*$

---

왜? $TT^*= T^*T$?
사실 충분히 관찰하지 않으면, 저런 생뚱맞은 정의를 이해하기는 어려우니, 먼저 다음을 살펴보길 바란다.

• $A$가 normal이면, $A^*$도 normal이다.
• $A$가 normal이면, $A + \lambda I$도 normal이다.여기서, $\lambda \in \mathbb{C}$ 그리고 $I$는 단위 행렬이다.

$(A - \lambda I)(A^* - \overline{\lambda} I) = A \cdot A^* - \overline{\lambda} A - \lambda A^* + |\lambda|^2 I$

$= A^* \cdot A - \lambda A^* - \overline{\lambda} A + |\lambda|^2 I$

$= (A^* - \overline{\lambda} I)(A - \lambda I)$

• 질문! 임의의 두 normal operator $A:V\to V$와 $B : V \to V$의 합 $A+B$는 normal 인가?

일반적으로, 두 정규 연산자의 합은 반드시 정규 연산자가 아닐 수 있다. 물론 이는 정규 행렬의 경우도 마찬가지이다. 두 대칭행렬의 합이 자명히 대칭행렬인 것과 차이가 있음을 주목하자.

• 임의의 linear operator $V\to V$는 두 허미션(self adjoint) 연산자 $A,B$에 대해서 다음과 같이 적을 수 있다.

  $A+ Bi$

• 이때, (허미션) $A,B$가 동시 대각화 가능할 필요 충분 조건은, $A$와 $B$가 가환하는 것이다. 즉, $AB = BA$일 때 $A$와 $B$는 동시 대각화 가능하다.

• 한편, $A+Bi$가 normal인 것과 $AB = BA$는 동치이다.

양자역학의 공리에서는 허미션 연산자(Self Adjoint)를 근본적인 것으로 간주한다. 그런 관점에서 정규연산자는 단순히 서로 영향을 주지 않는 (가환하는) 두 허미션연산자 $A, B$에 대해서 $A +iB$에 불과하다.

허미션 행렬 관찰 그리고 주요 정리들

양자역학에서는, 허미션 행렬은 에너지나 위치 같은 물리적인 양을 표현하는 데 사용된다. 그리고 이 행렬의 특별한 성질 덕분에, 이 행렬로 표현된 물리적인 양(고유값으로)은 항상 실제로 존재하는 숫자(우리가 실수라고 부르는)를 가지게 된다. 이런 기술 방식이 유용한 예시는 수소원자의 스펙트럼이다. 그의 불연속적인 에너지 준위는 허미션 행렬의 고유값들의 집합으로 표현될 수 있다. (사실 무한히 많은 에너지 준위를 가진다.)

왜 우리는 고유값에 관심을 갖는가?

예제 (Sturm-Liouville problem)

다음의 최소값을 구하여라, $f \in C^2$, $f(0)=0$ 그리고 $f(1)=0$ 일때,

$\int |f'(x)|^2 dx$ with contraint $\int |f(x)|^2 dx =1$

챗 지피티의 풀이

이 문제는 변분 원리와 라그랑주 승수법을 사용하여 고유값 문제로 해결됩니다.

1. 최적화 문제로 설정: 주어진 함수 $f(x)$의 도함수의 제곱에 대한 적분 $\int |f'(x)|^2 dx$을 최소화하는 문제를 설정합니다. 이때 $f(x)$의 정규화 조건 $\int |f(x)|^2 dx = 1$이 주어집니다.

2. 라그랑주 함수 정의: 제약 조건을 고려하여 라그랑주 함수를 정의합니다.
   $\mathcal{L}(f, \lambda) = \int |f'(x)|^2 dx - \lambda \left(\int |f(x)|^2 dx - 1\right)$

3. 변분 계산: $\mathcal{L}$에 대해 변분을 수행하여 고유값 문제로 변환합니다. 이로 인해 얻어지는 방정식은 다음과 같습니다.
   $-f''(x) = \lambda f(x)$
   이는 슈투름-리우빌(Sturm-Liouville) 형태의 고유값 문제입니다.

4. 고유함수와 고유값: 경계 조건 $f(0) = 0$ 및 $f(1) = 0$을 만족하는 가장 작은 고유값을 가진 고유함수는 $f(x) = \sin(\pi x)$이며, 이때 고유값은 $\lambda = \pi^2$입니다.

따라서, 주어진 문제의 최소값은 $\pi^2$입니다.

(GPT)의 풀이는 논리적이지도 않고, 갑자기 계산한 고유값이 최소값이라고 우기는 등, 매우 빈틈이 많은 풀이이나, 굳이 수정하지 않고 그대로 여기 게시했다. 왜냐하면, 이 글의 목적은 저 문제를 소개하고 푸는 것이 아니니까...

---

고유값은 양자역학에서 매우 중요한 역할을 한다. 예를 들어, 수소 원자의 바닥 상태 에너지를 구하는 과정에서 고유값 문제는 핵심적인 위치를 차지한다. 다음 방식으로 기술할 수 있다.

• 우선 최적화 문제로 기술하면:
  수소 원자의 바닥 상태 에너지는 다음과 같이 해밀토니안 $H$의 기대값을 최소화함으로써 얻어진다:
  $E_0 = \min_{\psi} \left( \frac{\langle \psi | H | \psi \rangle}{\langle \psi | \psi \rangle} \right)$
  이 과정은 실제로 라그랑주 승수를 도입하여 제약 조건(정규화 조건$\| \psi \|=1$)을 고려하는 최적화 문제로 나타낼 수 있다.

• 고유값 문제로 자연스럽게 전환된다.:
  정규화 조건 을 만족시키면서, 최적화 문제를 풀기 위해서 라그랑주 승수를 도입한 라그랑주 함수를 정의하자.
  $\mathcal{L}(\psi, \lambda) = \langle \psi | H | \psi \rangle - \lambda (\langle \psi | \psi \rangle - 1)$
  여기에서 변분을 적용하면 수식 (57), Schollwöck 강의노트 , 수소 원자의 바닥 상태 에너지는 해밀토니안 연산자 $H$의 가장 작은 고유값을 찾는 문제로 이어진다.
  $H \psi = E \psi$

대칭행렬의 아름다움( 라그랑주 승수법의 선형대수적 측면 )
수소 원자의 바닥 상태 구하기는 양자 물리학 역사상 매우 중요한 예시이고 다양한 풀이법을 알 필요가 있다. (그러나 필자는 알지 못한다.) 다만, 양자역학에 의해서, 이 문제가 수학적으로 우아한 방식으로 기술할 수 있게 되었다는 것을 감상할 뿐이다. 특히, 선형대수의 기본 개념인 대칭행렬과 고유값을 관찰하면, 깊은 직관을 얻을 수 있다. 독자가 위의 수소원자 예시와 잘 비교해서 직관을 얻어갈만한 정리를 소개한다.

정리 레이리 몫(Rayleigh quotients)
임의의 $n \times n$ 대칭 행렬 $A$에 대해,

$\lambda_{\min}(A) \leq \frac{\mathbf{x}^T A \mathbf{x}}{\mathbf{x}^T \mathbf{x}} \leq \lambda_{\max}(A),$

모든 $\mathbf{x} \neq 0$에 대해 성립한다.

또한,

$\lambda_{\max}(A) = \max_{|\mathbf{x}| = 1} \mathbf{x}^T A \mathbf{x}, \quad \lambda_{\min}(A) = \min_{|\mathbf{x}| = 1} \mathbf{x}^T A \mathbf{x}$

이며, 최대값과 최소값은 각각 $\mathbf{x} = \mathbf{v}_1$일 때와 $\mathbf{x} = \mathbf{v}_n$일 때 달성된다. 여기서 $\mathbf{v}_1$ (또는 $\mathbf{v}_n$)는 $A$의 가장 큰 (또는 가장 작은) 고유값에 대응하는 단위 노름 고유벡터이다.

---

양자역학에서 허미션 연산자가 필수적인 이유는, 허미션 연산자가 대칭 행렬의 특성을 지니기 때문이다. 구체적으로 말해서, 시스템의 에너지 상태를 기술하는 최적화 문제를 고유값 문제로 전환하도록 해준다.

---

허미션 행렬 살펴보기

슈르 삼각화는 스펙트럴 정리를 증명하는데 있어서 매우 중요한 도구이다. (물론 슈르 삼각화를 거치지 않고도 스펙트럴 정리를 증명을 기술 할 수 있다.)

예시 1

행렬 $A = \begin{pmatrix} 8 & -1 \\ -6 & 7 \end{pmatrix}$를 슈어 삼각화를 해보자.

$\text{det}(A - \lambda I) = 0.$

$\begin{vmatrix} 8 - \lambda & -1 \\ -6 & 7 - \lambda \end{vmatrix} = (8 - \lambda)(7 - \lambda) - (-1)(-6) = \lambda^2 - 15\lambda + 50 = 0$

• Normalized eigenvector $u_1$과 $u_1$과 직교인 벡터 $v_2$를 고르자.
  고유값 $\lambda_1 = 10$에 대응하는 고유벡터 $u_1$으로서 다음과 같이 고르자.

$u_1 = \frac{1}{\sqrt{5}} \begin{pmatrix} 1 \\ -2 \end{pmatrix}$ 그리고 $v_2 = \frac{1}{\sqrt{5}} \begin{pmatrix} -2 \\ 1 \end{pmatrix}$.

• $B=\{u_1, v_2\}$가 직교 기저임을 기억하자.

행렬 $A$는 선형변환 $x \mapsto A x$의 standard 기저 표현이다. 이 선형변환을 기저 $B$에 대해서 다시 표현하면 자명히 삼각행렬이 될 것이다. 굳이 이 기저변환을 계산으로 표현하면 다음과 같다.

$[A]_{\{u_1, v_2\}}=U^{-1}AU$, 여기서 $U=\begin{pmatrix} u_1 & v_2 \end{pmatrix} = \frac{1}{\sqrt{5}} \begin{pmatrix} 1 & 2 \\ -2 & 1 \end{pmatrix}.$

한편, $U$는 유니타리 행렬이므로, $U^{-1}$은 $U^\dagger$이다. 따라서, 쉽게 계산이 되고 계산 결과는 다음과 같다.

$[A]_{\{u_1, v_2\}}=U^{\dagger}AU=\begin{pmatrix} 10 & 5 \\ 0 & 5 \end{pmatrix}$

• 첫 대각 성분이 고유값 $\lambda_1=10$인 것은 자명하다. 그러나, 두번째 대각성분은 왜 $\lambda_2 = 5$인 이유는 뭘까? 이 질문에 대한 답이, 슈어 삼각화 증명의 핵심이다.

• 만약 $2\times 2$ 허미션행렬을 예시로 하는 경우, 첫번째 고유벡터 $u_1$과 직교인 벡터 $v_2$는 두번째 고유벡터가 된다. 이것은 허미션행렬의 (서로 다른 고유값에 대응하는) 고유벡터들은 (항상) 서로 직교한다는 성질에 기인한다. 따라서 이 경우 $B=\{u_1, v_2\}$에 대한 기저변환은 대각화이다. 즉, $2\times 2$ 대칭행렬을 슈어 삼각화하면 언제나 대각행렬이 된다. 이 관찰은 허미션행렬에 대한 스펙트럴 정리 증명의 핵심이된다.