개요

행렬식이 행렬보다 더 먼저 탄생한 개념입니다. 역사적 관점에서 보면, 행렬식을 계산하기 위해서 행렬이 도입된것이죠.

행렬식은, 선형변환의 (또는 선형시스템의) 특성을 나타내는 값입니다. 그렇다면, 그 특성이란 무엇일까요? 행렬식의 의미를 매우 간략하게 요약해 보았습니다. (이 순서대로 이해해 나가시길 추천드립니다.)

1. 부피: 행렬식은 선형변환에 의해 어떤 영역의 부피가 어떻게 변하는지를 나타냅니다. 어떤 행렬의 행렬식이 1보다 크면, 그 행렬은 영역을 확대시키는 효과를 가지며, 행렬식이 1보다 작으면 영역을 축소시키는 효과를 가집니다. 행렬식이 0이라면, 영역이 평면에 수축되어 점 또는 선으로 변환됩니다. (영상참고)

2. 선형변환의 합성 그리고 역변환 (행렬식의 곱과 역행렬): 두 개의 행렬을 곱할 때, 그들의 행렬식은 곱한 행렬식의 곱과 같습니다. 또한, 정방행렬의 역행렬이 존재하는 경우, 역행렬의 행렬식은 원래 행렬의 행렬식의 역수입니다.

3. 선형 시스템의 해: 주어진 선형 시스템의 행렬이 정방행렬 A라고 하고, 우변 벡터를 b라고 할 때, Ax = b 형태의 방정식을 고려합니다. 행렬 A의 행렬식이 0인 경우, 즉 det(A) = 0이면 이 시스템의 해가 없거나 무수히 많습니다. 행렬 A의 행렬식이 0이 아니라면 (det(A) ≠ 0) A의 역행렬을 사용하여 유일한 해 $x = A^{-1}b$를 구할 수 있습니다.

치역 (Image)과 영공간 (Kernel): 선형변환은 벡터공간에서 다른 벡터공간으로의 매핑을 나타냅니다. 이때 중요한 개념으로 치역과 영공간이 있습니다. 중요: 선형변환의 치역(image)와 영공간(kernel)은 언제나 벡터공간입니다.
치역 (Image): 선형변환$T:V \to W$을 통해 얻어지는 모든 가능한 결과 $T(v)$ 벡터들의 집합을 치역이라고 합니다. 식으로, 간단히 $T(V)$ 또는 $\text{image}T$라 적으며, 이는 공역 ($W$)의 부분 공간이 됩니다.
영공간 (Kernel): 영공간은 선형변환$T$에 대해서 $T(v)=\bold 0$의 해가 되는 벡터들의 집합을 나타냅니다. 영공간은 선형변환의 미지의 벡터에 해당하는 해의 집합이 됩니다. 식으로 간단히 $\text{ker} T$라고 적으며, 이는 정의역 ($V$)의 부분공간이 됩니다.
Rank-Nullity 정리는 선형대수학에서 매우 중요한 결과 중 하나로, 선형변환의 치역과 영공간 사이의 차원 관계를 나타내는 정리입니다.Rank-Nullity 정리는 다음과 같이 표현됩니다:
Rank-Nullity 정리: 선형변환 $T: V \to W$가 있을 때, dim(Image(T)) + dim(Ker(T)) = dim(V)
여기서 Image(T)는 선형변환 T의 치역 (Image)을 나타내고, Ker(T)는 선형변환 T의 영공간 (Kernel)을 나타냅니다.

4. 행렬식이 0이 아닐 때 행렬식이 0이 아닌 경우, 선형변환은 역변환이 존재합니다. 이는 해당 선형변환이 일대일 대응을 보장한다는 의미입니다. 다시 말해, 모든 입력에 대해 유일한 출력이 존재하고, 그 역도 성립합니다. 다시말해서, 치역 (image)의 차원은 정의역 (domain)의 차원과 같습니다. 그리고 영공간의 차원은 0입니다.

5. 행렬식이 0일 때 - 차원 축소: 행렬식이 0인 경우, 선형변환은 더 낮은 차원으로의 변환을 나타냅니다. 이는 입력 공간의 차원을 낮추는 효과를 가집니다. 다시말해서, 치역 (image)의 차원은 정의역 (domain)의 차원보다 작습니다. 그리고, 영공간의 차원이 0보다 큽니다.

행렬식은, 미적분학(그리고 기초미분기하학)에서 매우 중요한 역할을 합니다.

6. 변수변환 및 Jacobian: 다변수 미적분에서 변수변환을 할 때, Jacobian이 사용됩니다. 이때 Jacobian은 (특별한 의미를 가진) 행렬식에 지나지 않습니다. Jacobian은 변수 변환의 미분에 관련된 중요한 정보를 제공합니다.
7. Cross Product(외적) : 벡터 외적은 3차원 공간에서 주어진 두 벡터의 직교하는 성분을 계산하는 연산입니다. 벡터 a와 b의 외적은 $\bold a × \bold b$로 나타낼 수 있는데, 이 외적 결과는 행렬식의 관점에서 해석될 수 있습니다. 1. $\bold a\times \bold b$의 크기는 $\bold a$와 $\bold b$가 생성하는 평행사변형의 면적입니다. 2. $\bold a\times \bold b$의 방향은 그 평행사변형과 직교하는 방향을 나타냅니다.

(미분 기하학에서의) 교대 텐서는 행렬식을 추상화 한 개념으로 보면 됩니다. 그런 점에서, 행렬식은 미분기하학에서도 매우 중요한 역할을 합니다. 다시 처음으로 돌아와서, 행렬식이 왜 부피라는 의미를 가지는가에 대한 답을 찾으러 가봅시다.

8. 교대 텐서와 외대수 (Exterior Algebra):

• 교대 텐서와 행렬식: 먼저, 행렬식을 다시 공부하는 과정이 필요합니다. 정방행렬을 행벡터 $n$개를 모은 것이라고, 보면 행렬식은 $n$개의 벡터를 입력으로 하는 함수로 생각할 수 있습니다. 이 관점에서, 행렬식은 교대 텐서로 표현됩니다. 조금 더, 구체적으로 말해서, 미분기하학에서는 미적분학의 Jacobian 대신에, 교대텐서를 사용하는 것말고는 달라지는게 없습니다.

• 외대수 (Exterior Algebra): 외대수는 벡터의 외적(Cross product)을 일반화(정확한 표현은 아닌 점 양해 부탁해요::외적(cross product)에서는 외적의 결과가 벡터이지만, 사실 그것은 3차원에서만 가능한 현상입니다)한 개념으로, 기하학적 성질(ex 공간의 부피)를 구하는데 사용합니다. 미적분학에서, 외적(cross product)을 하는 맥락은 곡면의 접평면을 표현하기 위해서, 접벡터(독립인) 2개를 외적했습니다. 마찬가지로, 미분기하학에서도, 접벡터들을 이용해서 접공간의 성질을 구하고자 외대수를 사용합니다.

• 미분형식 : 미분형식은, (미적분학에서, $dS$를 $dx dy$의 식으로 바꾸는 과정에서 접벡터의 외적을 사용하듯이) 그 자체로 외대수의 결과입니다. 미적분학에서 배우는 모든 것은, 결국 미적분학의 기본정리에 의의가 있습니다. 마찬가지로, 미분형식을 이해하는 것은, 미적분학의 기본정리를 이해하는 것과 매우 깊게 연관이 있습니다. (스토크스 정리, 그린의 정리 등의 미적분학의 중요한 결과를 미분 형식을 통해 더 간결하게 표현할 수 있습니다.)

행렬식

더 추상적인 방식의 정의는, 증명서술에 매우 도움이 되지만, 교육적으로는 좋지 않습니다. (예를들어, 수학계의 노벨상인 필즈상을 5번이나 수상한 Bourbaki (1998)는 외대수를 이용해서, 행렬식을 정의하였습니다.) 반면에, 구체적인 정의는 교육적으로는 훌륭하지만, 그것으로 증명을 서술하기에는 너무 지저분합니다. 예를들어서, 2007 개정 교육 과정의 기하와벡터 교과서에서는, $2\times2$행렬만 다루며 행렬 $\left(\begin{matrix}a & b \\ c &d\end{matrix}\right)$에 대해서 $ad-bc\ne 0$이라는 조건 하에, 역행렬$\frac{1}{ad-bc}\left(\begin{matrix}d & -b \\ -c &a\end{matrix}\right)$을 정말로 연립방정식을 풀어서 유도합니다.

행렬식의 예시

예시: 1x1 행렬의 행렬식

A가 스칼라인 경우입니다, det(A) = A로 정의합니다.

예시: 2x2 행렬의 행렬식

다음과 같은 2x2 행렬을 생각해봅시다:
$\left(\begin{matrix}a & b \\ c &d\end{matrix}\right)$
이 행렬의 행렬식은 $ad - bc$로 계산됩니다.

예시: 3x3 행렬의 행렬식

다음과 같은 3x3 행렬을 생각해봅시다:
$\left(\begin{matrix}a & b &c\\ d &e&f\\g&h&i\end{matrix}\right)$
이 행렬의 행렬식은 "사루스 법칙(Sarrus Rule)"을 사용하여 계산할 수 있습니다:
$det(A) = aei + bfg + cdh - ceg - bdi - afh$

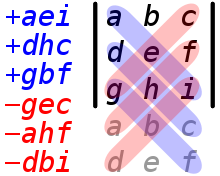
또 다른 방법은 라플라스전개입니다. 예를 들어, 위에서 주어진 3x3 행렬의 행렬식을 계산하려면, 첫 번째 행을 선택해서 라플라스 전개를 수행할 수 있습니다:

$det(A) = a \cdot det\left(\begin{matrix}e & f \\ h & i\end{matrix}\right) - b \cdot det\left(\begin{matrix}d & f \\ g & i\end{matrix}\right) + c \cdot det\left(\begin{matrix}d & e \\ g & h\end{matrix}\right)$

이렇게 작은 부분 행렬들의 행렬식을 계산하면서 라플라스 전개를 진행하고, 마지막에 2x2 행렬의 행렬식을 사용하여 계산합니다. 이렇게 라플라스 전개를 적용하여 3x3 행렬의 행렬식을 계산할 수 있습니다.

연습문제

다음 두 행렬을 생각해봅시다:

$A = \begin{bmatrix} 2 & 3 \\ 2 & 3 \end{bmatrix}$

$B = \begin{bmatrix} 4 & 1 \\ 4 & 1 \end{bmatrix}$
각각의 행렬에 대한 행렬식을 계산해보겠습니다.

$det(A) = 2 \cdot 3 - 2 \cdot 3 = 0$
$det(B) = 4 \cdot 1 - 4 \cdot 1 = 0$

다음 3x3 행렬을 생각해봅시다:

$C = \begin{bmatrix} 1 & 1 & 1 \\ 4 & 6 & 2 \\ 2 & 3 & 1 \end{bmatrix}$

$det(C) = 1\cdot(6 \cdot 1 - 2 \cdot 3) - 1\cdot( 4\cdot 1 - 2 \cdot 2) + 1\cdot(4 \cdot 3 - 6 \cdot 2) = 0$

이렇게 두 행이 일치하는 경우, 또는 어떤 행이 다른 행의 상수배인 경우 그 행렬의 행렬식은 0입니다. 왜 그럴까요? 그 이유를 행렬식의 의미를 곰곰히 생각하여, 직관적으로 이해하는 것이 매우 중요합니다.

행렬식의 정의

그럼, 더 큰 사이즈의 행렬의 행렬식은 어떻게 될까요?

대칭군을 이용한 행렬식의 정의 (Leibniz formula for determinants)

이 정의는 행렬의 원소들을 대칭군의 순열(permutation)로 나타내고, 이 순열에 따른 부호와 원소들의 곱의 합으로 행렬식을 계산합니다.

$n$차 정방행렬 $A$의 행렬식은 다음과 같이 Leibniz 공식을 이용하여 정의됩니다:

$\det(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \cdot a_{1\sigma(1)} \cdot a_{2\sigma(2)} \cdot \ldots \cdot a_{n\sigma(n)}$

여기서 $S_n$은 $n$개의 원소를 가지는 대칭군(대칭 그룹)이며, $\sigma$는 $S_n$의 순열입니다. $\text{sgn}(\sigma)$는 순열 $\sigma$의 부호(sign)를 나타내며, $a_{ij}$는 $A$의 $i$행 $j$열의 원소입니다.

이 정의는 행렬식을 순열을 (대칭군을) 이용해서 표현하는 방법으로, 각 순열은 원소들의 위치를 바꾸는 변환이며, 부호와 곱의 합을 통해 행렬식을 계산합니다.

순열이란?

순열(permutation)이란 어떤 집합의 원소들을 일렬로 나열하는 것을 의미합니다. 순열은 원소의 순서가 중요하며, 같은 원소들을 다르게 배열하면 서로 다른 순열이 됩니다. 순열의 다른 표현 방법으로,1대1 대응 함수를 사용하기도 하는데, Leibniz 공식에서 $\sigma$가 여기에 해당합니다. 예를 들어, 집합
$\{ 1 , 2 , 3 \}$
의 원소들을 나열하는 모든 순열은 각각 다음을 만족하는 1대1 대응 함수 $\sigma:\{ 1 , 2 , 3 \}\to \{ 1 , 2 , 3 \}$에 대응합니다.

• 1, 2, 3 : $\sigma(1)=1$, $\sigma(2)=2$ 그리고 $\sigma(3)=3$인 함수 $\sigma$
• 1, 3, 2 : $\sigma(1)=1$, $\sigma(2)=3$ 그리고 $\sigma(3)=2$인 함수 $\sigma$
• 2, 1, 3 : $\sigma(1)=2$, $\sigma(2)=1$ 그리고 $\sigma(3)=3$인 함수 $\sigma$
• 2, 3, 1 : $\sigma(1)=2$, $\sigma(2)=3$ 그리고 $\sigma(3)=1$인 함수 $\sigma$
• 3, 1, 2 : $\sigma(1)=3$, $\sigma(2)=1$ 그리고 $\sigma(3)=2$인 함수 $\sigma$
• 3, 2, 1 : $\sigma(1)=3$, $\sigma(2)=2$ 그리고 $\sigma(3)=1$인 함수 $\sigma$

순열의 부호란?

$n$개의 원소를 가지는 순열에 대한 부호는 순열에서 쌍을 교환해야 하는 횟수에 따라 결정됩니다. 교환 횟수가 짝수면 부호는 +1이고, 홀수면 부호는 -1입니다. 예를 들어, 순열 1,3,2를 살펴보겠습니다. 이 순열은 기본 순서인 1,2,3에서 두 번째와 세 번째 원소의 위치를 바꿔 생성할 수 있습니다. 따라서 한 번의 전환만 필요합니다. 전환의 수가 홀수이므로 이 순열의 부호는 -1입니다.

순열의 부호를 어떻게 계산하나?

1. 교환 횟수 계산: 순열을 정렬된 순서로 만들기 위해 필요한 쌍의 교환 횟수를 계산합니다. 짝수 번의 교환을 요구하는 순열은 양의 부호를 가지고, 홀수 번의 교환을 요구하는 순열은 음의 부호를 가집니다.

2. 사이클 계산:

   주어진 순열의 임의의 위치에서 시작해서, 그 위치에 적혀있는 수에 해당하는 위치로 이동하기를 반복하면, 언젠가 시작위치로 돌아오게 되어있습니다. 예를들어서 3, 1, 2의 경우 1번(3이적혀있음)->3번(2가 적혀있음)->2번(1이 적혀있음)->1번 이렇게 말이죠. 이런경우, $(1,3,2)$라고 표기합니다. 주의 : 기본순서에 해당하는 1,2,3은 사이클$(1,2,3)$이 아닙니다. 사이클$(1,2,3)$은 순열 2,3,1의 또다른 표현입니다.

   순열을 여러 개의 (서로서로 곂치지 않는) 사이클로 분해할 수도 있습니다. 사이클의 길이가 홀수면 부호는 1, 짝수면 부호는 -1입니다. 그리고 분해를 구성하는 각각의 사이클의 부호를 모두 곱하면, 순열의 부호를 구할 수 있습니다. 예를들어서, 순열 2, 5, 4, 3, 1은 다음과 같이 표현할 수 있습니다.
   $(1,2,5)(3,4)$
   그러므로, 순열 2, 5, 4, 3, 1의 부호는 $-1$입니다.

큰 순열의 경우 어떻게 할까?

순열의 부호를 결정하는 것은 그 자체로 꽤 깊은 주제입니다. 큰 순열에서도 이를 효과적으로 계산할 수 있는 여러 방법이 있습니다.

큰 순열의 경우, 그냥 교환 횟수를 계산하는 방법은 복잡도가 $O(n^2)$가 될 수 있으므로, 효율적인 알고리즘을 사용하는 것이 중요합니다.

예를 들어, 병합 정렬(Merge Sort)와 같은 정렬 알고리즘을 사용하여 교환 횟수를 $O(n \log n)$의 복잡도로 계산할 수 있습니다.

라플라스 전개를 이용한 행렬식 정의

라플라스 전개를 이용한 행렬식 정의는 행렬을 작은 부분 행렬로 분해하고, 이들의 행렬식을 이용하여 원래 행렬의 행렬식을 계산하는 방법입니다. 라플라스 전개를 이용한 행렬식 정의는 재귀적인 방식으로 행렬식을 계산하며, 작은 차원의 행렬식을 이용하여 큰 차원의 행렬식을 구할 수 있습니다.

$n$차 정방행렬 $A$의 행렬식은 다음과 같이 라플라스 전개를 통해 정의됩니다:

$\det(A) = \sum_{i=1}^n a_{ij} \cdot C_{ij}$

여기서 $a_{ij}$는 $A$의 $i$행 $j$열의 원소입니다. $C_{ij}$는 $a_{ij}$의 여인수(cofactor)로서, $a_{ij}$를 제외한 나머지 부분행렬의 행렬식을 의미합니다. 여인수는 작은 차원의 행렬식을 이용하여 계산되며, 다음과 같이 정의됩니다:

$C_{ij} = (-1)^{i+j} \cdot \det(M_{ij})$

여기서 $M_{ij}$는 $A$의 $i$행과 $j$열을 제외한 부분행렬(submatrix)입니다. 이렇게 계산된 여인수를 이용하여 라플라스 전개를 통해 행렬식을 구할 수 있습니다.

계산예시

두 방법 모두 같은 결과를 얻을 수 있으며, 실제로는 계산에 두 방법을 사용하는 경우는 거의 없습니다. 그러나, 두 방법을 이해하는 것이 매우 중요하기 때문에, 계산을 상세히 설명하도록 하겠습니다.

다음과 같은 3x3 행렬을 고려해봅시다:

Leibniz 공식을 사용한 계산:

Leibniz 공식에 따라, 모든 순열을 고려하고 해당 순열의 부호를 곱한 후 각 행렬 항목의 곱을 계산해야 합니다.

이 행렬에 대한 Leibniz 공식을 사용한 계산에서 순열을 고려해봅시다:

1. $\textcolor{blue}{1, 2, 3}$: 양수 부호, 곱 = $A_{1\textcolor{blue}{1}}A_{2\textcolor{blue}{2}}A_{3\textcolor{blue}{3}} = 2 \cdot (-1) \cdot 0 = 0$
2. $\textcolor{red}{1, 3, 2}$: 음수 부호, 곱 = $A_{1\textcolor{red}{1}}A_{2\textcolor{red}{3}}A_{3\textcolor{red}{2}} = 2 \cdot 2 \cdot 4 = 16$
3. $\textcolor{red}{2, 1, 3}$: 음수 부호, 곱 = $A_{1\textcolor{red}{2}}A_{2\textcolor{red}{1}}A_{3\textcolor{red}{3}} = 1 \cdot 0 \cdot 0 = 0$
4. $\textcolor{blue}{2, 3, 1}$: 양수 부호, 곱 = $A_{1\textcolor{blue}{2}}A_{2\textcolor{blue}{3}}A_{3\textcolor{blue}{1}} = 1 \cdot 2 \cdot 1 = 2$
5. $\textcolor{blue}{3, 1, 2}$: 양수 부호, 곱 = $A_{1\textcolor{blue}{3}}A_{2\textcolor{blue}{1}}A_{3\textcolor{blue}{2}} = 3 \cdot 0 \cdot 4 = 0$
6. $\textcolor{red}{3, 2, 1}$: 음수 부호, 곱 = $A_{1\textcolor{red}{3}}A_{2\textcolor{red}{2}}A_{3\textcolor{red}{1}} = 3 \cdot (-1) \cdot 1 = -3$

이제 결과를 더합니다:

$0 - 16 - 0 + 2 + 0 - (-3) = -11$

Laplace 전개를 사용한 계산:

Laplace 전개 방법을 사용하여 행렬식을 계산할 수도 있습니다. 첫 번째 행을 기준으로 전개해보겠습니다:

2x2 행렬의 행렬식을 계산하면:

이 행렬식을 다시 Laplace 전개 공식에 대입하면:

따라서, 행렬 A의 행렬식은 -11이 됩니다. 이 값은 Leibniz 공식을 사용하여 구한 결과와 일치합니다.

의의

Leibniz 공식과 라플라스 전개는 행렬의 행렬식을 계산하는 방법으로 사용하기에, 비효율적입니다. Leibniz 공식은 모든 가능한 순열을 고려해야 하며, 라플라스 전개는 재귀적인 계산을 필요로 하기 때문입니다.

그럼에도 불구하고, 이러한 방법들은 행렬식의 구조와 성질에 대한 근본적인 이해를 제공하고 있습니다. 실제 계산에는 더 효율적인 방법이 사용되지만, 이러한 고전적인 방법들의 이해는 중요합니다.

행렬식의 성질과 그 증명

행렬식에 대한 개념을 아는 대로 정리해보시고 글을 읽으시면 도움일 될 것이라 생각합니다.

행렬식의 기본성질

1. 단위행렬의 행렬식 = 1

단위행렬(I)는 대각선 원소가 모두 1이고 나머지 원소는 0인 정방행렬입니다. 단위행렬의 행렬식은 항상 1입니다.

2. 행의 교환

두 행을 교환하면 행렬식의 부호가 바뀝니다. 예를 들어, 행렬 $A$의 행렬식이 $\text{det}(A) = d$라면, 두 행을 교환한 행렬$B$의 행렬식은 $\text{det}(B) = -d$가 됩니다.

3. 다중 선형성

행렬식은 각 행에 대한 선형 함수입니다. 이 의미는, 행렬 $A$의 한 행을 두 개의 벡터의 선형 결합으로 표현할 수 있다면, 그 행렬의 행렬식은 각 벡터에 대한 행렬식의 선형 결합과 동일하다는 것입니다.

수학적으로, 행렬 $A$의 $i$행이 $\alpha \mathbf{u} + \beta \mathbf{v}$로 표현된다면, 행렬식은 다음과 같이 표현됩니다:

$\text{det}(A) = \alpha \cdot \text{det}(A_{\mathbf{u}}) + \beta \cdot \text{det}(A_{\mathbf{v}})$

여기서 $A_{\mathbf{u}}$와 $A_{\mathbf{v}}$는 $A$의 $i$행이 각각 $\mathbf{u}$와 $\mathbf{v}$로 대체된 행렬입니다.

기본행렬의 행렬식

기본 행렬(elementary matrices)은 행렬의 기본 행 연산을 나타내는 행렬입니다. 기본 행 연산에는 행의 교환, 행에 스칼라를 곱하기, 한 행에 다른 행의 배수를 더하기 등이 포함됩니다.

기본 행렬의 종류와 그에 따른 행렬식은 다음과 같습니다:

1. 행의 교환 (Row Interchange)

행렬에서 두 행을 교환하는 것을 나타내는 기본 행렬은 특정 두 행만 1이 위치를 바꾸고 나머지는 단위행렬의 형태를 가집니다. 이러한 행렬의 행렬식은 -1입니다.

예시: $\begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}$

2. 행에 스칼라 곱하기 (Row Scaling)

한 행에 스칼라를 곱하는 것을 나타내는 기본 행렬은 대각선 원소 중 하나만 스칼라 값이고 나머지는 단위행렬과 같습니다. 이러한 행렬의 행렬식은 그 스칼라 값입니다.

예시 (두 번째 행에 2를 곱하는 경우): $\begin{bmatrix} 1 & 0 \\ 0 & 2 \\ \end{bmatrix}$

3. 한 행에 다른 행의 배수를 더하기 (Row Addition)

한 행에 다른 행의 배수를 더하는 것을 나타내는 기본 행렬은 대각선 원소는 모두 1이고, 특정 위치에 다른 행을 더하는 배수 값이 있습니다. 이러한 행렬의 행렬식은 1입니다.

예시 (첫 번째 행에 두 번째 행의 2배를 더하는 경우): $\begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix}$

위의 설명은 2x2 행렬을 예로 들었지만, 더 큰 행렬에도 적용됩니다.

기본 행렬을 통한 행렬식 계산

행을 스칼라로 곱할 때, 행렬식은 해당 스칼라로 곱해집니다.
두 행을 교환할 때, 행렬식의 부호가 바뀝니다.
한 행을 다른 행에 더할 때, 행렬식은 변하지 않습니다.

기본 행렬 (E)와 행렬식:

1. 행 교환을 하면 부호가 바뀝니다:
   • 행렬 $E$가 두 행을 교환하는 연산을 나타낼 때, $\det(E) = -1$입니다.
   • 따라서, 정방행렬 $B$에 대하여 $\det(EB) = -\det(B)$.
2. 행 스케일링을 하면 그만큼 행렬식이 스케일링 됩니다.:
   • 행렬 $E$가 한 행에 스칼라 $k$를 곱하는 연산을 나타낼 때, $\det(E) = k$입니다.
   • 따라서, 정방행렬 $B$에 대하여 $\det(EB) = k\det(B)$.
3. 한 행을 다른 행에 더하는 것은 행렬식에 영향을 주지 않습니다:
   • 행렬 $E$가 한 행에 다른 행의 스케일링 된 버전을 더하는 연산을 나타낼 때, $\det(E) = 1$입니다.
   • 따라서, 정방행렬 $B$에 대하여 $\det(EB) = \det(B)$.

이러한 성질들을 기반으로, 기본행렬 $E$에 대해서
$\det(EB) = \det(E)\det(B)$가 성립함을 알 수 있습니다.

기본 행렬의 행렬식이 위와 같이 주어진다는 것을 알면, 기본 행렬의 연속적인 곱을 사용하여 어떤 행렬 $A$의 행렬식을 계산할 수 있습니다. 따라서, $A$의 행렬식은 기본 행렬들의 행렬식의 곱으로 나타낼 수 있습니다. 이 성질은 행렬 $A$가 가역적일 때, 즉 역행렬이 존재할 때에만 적용됩니다.

행렬식이 0일 필요충분조건

행렬의 행렬식이 0일 필요충분조건은 해당 행렬의 행 또는 열이 선형 종속인 것이다.
- 행렬의 행이 선형 종속인 것의 의미는 행렬의 한 행이 다른 행들의 선형 조합으로 표현될 수 있다는 것을 의미합니다. 예를 들어, 3x3 행렬에서 한 행이 다른 두 행의 합으로 표현될 수 있다면, 해당 행렬의 행들은 선형 종속이며, 그 행렬의 행렬식은 0입니다.
행렬이 비가역적일 필요충분조건은 해당 행렬의 행렬식이 0인 것이다.
- 행렬이 비가역적이라는 것은 해당 행렬의 역행렬이 존재하지 않는다는 것을 의미합니다.

1. 행렬식이 $0$일 때 비가역적임을 증명:

행렬 $A$의 행렬식이 $0$이라고 가정합시다.

행렬의 행렬식이 $0$인 것은 그 행렬의 행(또는 열)이 서로 선형종속이라는 것을 의미합니다. 선형종속이라는 것은 하나의 벡터(행 또는 열)가 다른 벡터들의 선형조합으로 표현될 수 있다는 것입니다.

이것을 가정하여, $A$의 열들 중 일부가 다른 열들의 선형 조합으로 표현된다고 하면, $A$에 어떤 벡터($\ne \bold 0$)를 곱하여 결과가 0 벡터가 되게 하는 경우가 존재하게 됩니다. 즉, $Ax = \bold 0$을 만족하는 $\bold x$가 존재합니다. 이때 $\bold x$는 $0$ 벡터가 아닙니다.

하지만, 만약 $A$의 역행렬이 존재한다면, $A^{-1}Ax = x = 0$이 되어야 합니다. 그런데 앞서 언급한 것처럼 $x$는 $0$ 벡터가 아니므로, 이것은 모순입니다.

따라서, 행렬 $A$의 행렬식이 $0$일 때 $A$는 비가역적입니다.

2. 행렬이 비가역적일 때 행렬식이 $0$임을 증명:

행렬 $A$가 비가역적이라고 가정합시다.

이것은 $A$의 역행렬이 존재하지 않는다는 것을 의미합니다. 따라서 $A$의 RREF는 단위행렬 일 수 없습니다. 즉, A의 몇몇 열들은 피벗 열이 아니고, (그러한 열들에 대응하는 변수가 자유변수가 되므로), $Ax = 0$을 만족하는 $0$ 벡터가 아닌 해 $\bold x$가 존재합니다.

만약 $A$의 행렬식이 $0$이 아니라면, 그것은 $A$의 행(또는 열)이 선형독립이라는 것을 의미합니다. 그런데 선형독립이라면, $Ax = 0$을 만족하는 유일한 해는 $\bold x = 0$ 벡터입니다.

하지만 앞서 언급한 것처럼 $0$ 벡터가 아닌 다른 해 $\bold x$가 존재하므로, 이것은 모순입니다.

따라서, 행렬 $A$가 비가역적일 때 $A$의 행렬식은 $0$입니다.

$det(A^\top)=det(A)$

이 증명에서는 순열의 역수와 그 부호의 성질, 그리고 행렬의 원소의 순서를 바꾸는 트릭을 활용하여 전치행렬의 행렬식과 원래 행렬의 행렬식이 동일하다는 것을 보여줍니다.

증명:

행렬식의 정의에 따라서, $n \times n$ 행렬 $A$의 행렬식은 다음과 같이 주어진다:

$\text{det}(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^{n} a_{i,\sigma(i)}$

여기서 $\sigma$는 순열을 나타내고, $S_n$은 n개의 요소에 대한 모든 가능한 순열의 집합입니다. $\text{sgn}(\sigma)$는 순열의 부호를 나타낸다. 그리고 $\prod_{i=1}^{n} a_{i,\sigma(i)}$은 $a_{1\sigma(1)}\ldots a_{n\sigma(n)}$을 간단하게 표현한 것이다.

$A^\top$의 i번째 행과 j번째 열의 원소는 $A$의 j번째 행과 i번째 열의 원소와 동일하므로, $A^\top$의 행렬식은 다음과 같이 주어진다:

$\text{det}(A^\top) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^{n} a_{\sigma(i),i}$

$\sigma:\{1,2,\ldots,n\}\to\{1,2,\ldots,n\}$가 1대1대응이기 때문에, 역함수$\sigma^{-1}$가 존재합니다.

한편, $\sigma$와 $\sigma^{-1}$의 부호가 같으므로,
$\text{sgn}(\sigma) \prod_{i=1}^{n} a_{\sigma(i),i}=\text{sgn}(\sigma^{-1}) \prod_{i=1}^{n} a_{\sigma(i),i}$

그리고 $\sigma(i)=j$에 대해 $i=\sigma^{-1}\left(j\right)$이므로 $(j=1,2,\ldots, n)$, $\prod_{i=1}^{n} a_{\sigma(i),i}=a_{\sigma(1)1}\ldots a_{\sigma(n)n}$의 곱하는 순서를 적절하게 바꾸어, $\prod_{i=1}^{n} a_{\sigma(i),i}=a_{1\sigma^{-1}(1)}\ldots a_{n\sigma^{-1}(n)}$이 성립함 확인할 수 있다.

따라서, $\text{det}(A^\top) = \sum_{\sigma \in S_n} \text{sgn}(\sigma^{-1}) \prod_{j=1}^{n} a_{j,\sigma^{-1}(j)}$이다. 이것을 $\text{det}(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^{n} a_{i,\sigma(i)}$과 비교하면 동일하므로($\because S_n=\{\sigma^{-1}\in S_n:\sigma \in S_n\}$), $\text{det}(A^\top)=\text{det}(A)$이다.

$det(AB)=det(A)det(B)$ 증명

행렬식의 곱셈에 대한 이 성질을 증명하기 위한 방법 중 일부를 설명하겠습니다. 여기서는 행렬식의 기본 성질 및 Leibniz 공식을 사용하는 방법을 주로 소개합니다.

1. 직접 계산으로 확인

이 방법은 2x2 행렬에서만 성립하며, 일반적인 증명에는 사용될 수 없습니다. 그러나 초기 이해를 도울 수 있습니다.

2. 기본 행렬을 통한 행렬식 계산을 이용

여기서의 주요 아이디어는 기본 행렬의 연속적인 곱을 통해 행렬 $A$의 행렬식을 계산하는 것입니다. 기본 행렬 (E_i)의 행렬식은 이미 알려져 있습니다(위에서 논의한 것처럼). 행렬 $A$가 가역적일 때, 행렬 $A$의 행렬식은 각 기본 행렬의 행렬식의 곱으로 나타낼 수 있습니다. 이러한 표현은 가우스 소거법과 기본 행 연산의 개념을 기반으로 합니다. 출처:proof2

기본 행렬을 통해 두 행렬의 곱에 대한 행렬식이 각 행렬의 행렬식의 곱과 동일함을 설명할 수 있습니다. 기본 행렬을 사용하여 행렬의 연산을 나타내면, 행렬식의 곱셈 속성을 확인하는데 유용합니다.

요약 설명:

두 행렬의 곱 $AB$의 행렬식과 각 행렬 $A$와 $B$의 행렬식의 곱이 동일함을 증명하기 위해 두 경우를 고려해볼 수 있습니다.

1. $A$가 가역적이지 않을 경우 (즉, 역행렬이 없을 경우):

   • 이 경우, $A$의 행렬식은 0입니다.
   • $AB$ 또한 가역적이지 않습니다. 그 이유는 만약 $AB$가 가역적이라면, $A$에도 오른쪽 역행렬이 존재하게 되어 모순이 발생하기 때문입니다.
   • 따라서 $AB$의 행렬식도 0입니다.
   • 결과적으로, $det(AB) = 0 = det(A)det(B)$.

2. $A$가 가역적일 경우 (즉, 역행렬이 있을 경우):

   • $A$는 기본 행렬의 곱$E_k \ldots E_1$으로 나타낼 수 있습니다. 이는 가우스 소거법을 사용하여 $A$를 (가역행렬의 RREF는 단위행렬이므로) 단위행렬로 변환시키는 과정을 통해 확인될 수 있습니다. 각 단계에서 기본 행 연산은 기본 행렬과의 곱셈으로 나타낼 수 있습니다.
   • 행렬 $AB=E_k\ldots E_1 B$입니다. 일반적으로 기본행렬 $E$에 대해서,
     $det(EB)=det(E)det(B)$이므로, 이 사실을 통해서 $AB=E_k\ldots E_1 B$의 행렬식은 다음과 같음을 증명합니다.
     $det(E_k\ldots E_1 B)=det(E_k)det(E_{k-1}\ldots E_1 B)=det(E_k)det(E_{k-1})det(E_{k-2}\ldots E_1 B)=\cdots=det(E_k)det(E_{k-1})det(E_{k-2})\cdots det(E_1)det(B)$
   • $det(E_k)det(E_{k-1})det(E_{k-2})\cdots det(E_1) det(I)=det(AI)=det(A)$이므로, 결과적으로 $det(AB) =det(A)det(B)$입니다. ($I$는 단위행렬)

3. 행렬식의 기본성질 활용

두 행을 교환하면 행렬식의 부호가 바뀐다는 것과, 다중 선형성을 활용하여 증명합니다. 사실, 이 증명은, 행렬식의 기본성질로부터 Leibniz 공식을 유도하는 과정 (그래서 중요)입니다.

증명:

1. $AB$의 $i$번째 행$(AB)_i$은 $B$의 행$B_j$들과 $A$의 i행의 성분들$a_{ij}$의 선형 결합으로 나타낼 수 있다.
   $(AB)_i = \sum_{j = 1}^n a_{ij} B_j$

2. 행렬식은 행들의 선형 결합을 통해 분배되므로: $AB$의 첫번째 행을 관찰하여 다음을 얻는다.

   $\det{AB} = \sum_{j_1 = 1}^n a_{1j_1}\det\left( \begin{bmatrix} B_{j_1} \\ AB_{[-1]} \end{bmatrix}\right)$

   여기서, $AB_{-1}$는 $AB$의 1번째 행을 제거해서 얻은 행렬이다. 그리고 $\begin{bmatrix} B_{j_1} \\ AB_{-1} \end{bmatrix}$의 두번째행은 $AB$의 두번째 행과 같으므로, 다음을 얻는다.

   $\det{AB} = \sum_{j_1 = 1}^n \sum_{j_2 = 1}^n a_{1j_1}a_{2j_2}\det\left( \begin{bmatrix} B_{j_1} \\ B_{j_2} \\ AB_{[-2]} \end{bmatrix}\right)$

   여기서, $AB_{[-2]}$는 $AB$의 1번째 행과 두번째 행을 제거해서 얻은 행렬이다. 이 과정을 반복하면, $AB$의 모든 행이 $B$의 행들중 하나로 대체될 것이다. 그러면 다음을 얻는다.

   $\det{AB} = \sum_{j_1,j_2,\ldots,j_n = 1}^n \prod_{k=1}^na_{kj_k} \det\left( \begin{bmatrix} B_{j_1} \\ B_{j_2} \\ \vdots \\ B_{j_n} \end{bmatrix}\right)$

3. 행렬 $\begin{bmatrix} B_{j_1} \\ B_{j_2} \\ \vdots \\ B_{j_n} \end{bmatrix}$에 대해서 같은 행들이 존재하면, 행렬식이 0이다. 즉, $\{j_1,\ldots,j_n\}=\{1,2,\ldots,n\}$이 아니고 (따라서) 더 적은 수의 원소를 가지면 행렬식이 0이된다. $\{j_1,\ldots,j_n\}=\{1,2,\ldots,n\}$인 경우는, 어떤 순열 $\sigma$가 존재해서, $j_i=\sigma(i)$를 만족시킨다.

4. 행렬식의 성질(교환을 할때마다, 부호가 뒤집힌다는 것)을 적용하여:
   $\det\left( \begin{bmatrix} B_{j_1} \\ B_{j_2} \\ \vdots \\ B_{j_n} \end{bmatrix} \right) = \text{sgn}(\sigma) \det(B)$
   여기서 $\text{sgn}(\sigma)$는 순열$j_1,j_2,\ldots,j_n$의 부호이다.

5.위의 식을 적용하면, 우리의 식은 다음과 같이 된다:
$\det{AB} = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{k=1}^n a_{k, \sigma(k)} \det(B)$

6. 다음과 같이 식을 변형할 수 있다:
   $\det{AB} = \left( \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{k=1}^n a_{k, \sigma(k)} \right) \det(B)$

7. 여기서, $\sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{k=1}^n a_{k, \sigma(k)}$는 $A$의 행렬식, 즉 $\det(A)$이다. (왜냐하면, 위 식에 $B=I$를 대입해도 식이 성립해야하니깐요)

8. 따라서, 다음과 같이 표현할 수 있다:
   $\det{AB} = \det(A) \det(B)$

이로써 $\det(AB) = \det(A)\det(B)$임을 증명했다.

4. Leibniz 공식활용

Leibniz 공식을 직접적으로 사용하면, 위의 증명보다 조금 더 직관적으로 바뀝니다. 두 행렬의 곱의 행렬식과 각 행렬의 행렬식의 곱을 직접비교하면, 두 식이 동일함을 확인할 수 있습니다. 출처:proof4

여인수전개를 이용한 역행렬계산

여인수 전개를 이용한 역행렬 계산은 행렬의 행렬식과 여인수 행렬을 활용하여 수행됩니다. 다음은 여인수 전개를 이용한 역행렬 계산 방법을 간단히 설명합니다:

1. 여인수 (cofactor) 정의:

행렬 $A$의 i행 j열 원소를 제거한 나머지 행렬의 행렬식에 $(-1)^{i+j}$를 곱한 값입니다. 이를 $C_{ij}$로 표시합니다.

2. 여인수 행렬 (Cofactor Matrix) $C$:

행렬 $A$에 대한 각 원소의 여인수로 구성된 행렬입니다. $C = [C_{ij}]$.

3. (고전적) 수반 행렬 (Adjugate or Adjoint Matrix) $\text{adj}(A)$:

여인수 행렬 $C$의 전치행렬입니다.

4. 역행렬 계산:

행렬 $A$가 가역적(즉, 행렬식이 0이 아닌 경우)이라면, $A$의 역행렬 $A^{-1}$는 다음과 같이 주어집니다:
$A^{-1} = \frac{1}{\text{det}(A)} \times \text{adj}(A)$

예제:

2x2 행렬의 경우, 여인수 전개를 이용한 역행렬 계산은 특히 간단합니다.

$A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$

여기서, $A$의 행렬식은:
$\text{det}(A) = ad - bc$

행렬 $A$의 역행렬은:
$A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

왜냐하면,

$C_{11} = d, \quad C_{12} = -c, \quad C_{21} = -b, \quad C_{22} = a$

따라서 여인수 행렬 $C$는:

$C = \begin{bmatrix} d & -c \\ -b & a \end{bmatrix}$

이 행렬의 전치를 얻기 위해 행과 열을 바꾸면 수반 행렬 $\text{adj}(A)$를 얻을 수 있습니다:

$\text{adj}(A) = \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

따라서, 역행렬 $A^{-1}$는:

$A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

행렬의 크기가 커질수록 여인수 전개를 통한 역행렬 계산은 복잡해집니다. 그러나 기본 원칙은 동일합니다.

$A^{-1} = \frac{1}{\text{det}(A)}\text{adj}(A)$

이 내용을 설명할때는, laplace 전개를 통한 행렬식이 매우 유용합니다. 이 글은, Laplace전개를 통한 행렬식과 Leibniz 공식으로 구한 행렬식이 같음을 전제로 합니다. 둘(Laplace, Leibniz)이 동일함에 대한 증명은 여기서 살펴보시기 바랍니다.

$A^{-1} = \frac{1}{\text{det}(A)}\text{adj}(A)$의 증명은 기본적으로 $A$와 $\text{adj}(A)$의 곱을 구하는 것입니다. 증명에 필요한 라플라스 전개를 이용하는 부분은 여인수를 정의하고 이를 통해 행렬식을 계산하는 과정에서 나옵니다.

주어진 $n \times n$ 행렬 $A$에 대해 다음과 같이 행렬을 표현해 봅시다:

$A = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{bmatrix}$

이때, $A$의 임의의 원소 $a_{ij}$에 대한 여인수 $C_{ij}$는 다음과 같습니다:

$C_{ij} = (-1)^{i+j} \text{det}(A_{ij})$

여기서 $A_{ij}$는 $a_{ij}$를 제외한 행렬로서 $a_{ij}$가 없는 $(n-1) \times (n-1)$ 행렬입니다.

수반 행렬 (adjugate or adjoint matrix) $\text{adj}(A)$는 각 원소가 여인수로 구성된 행렬의 전치입니다.

$\text{adj}(A) = \begin{bmatrix} C_{11} & C_{21} & \dots & C_{n1} \\ C_{12} & C_{22} & \dots & C_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ C_{1n} & C_{2n} & \dots & C_{nn} \end{bmatrix}$

이제 $A$와 $\text{adj}(A)$를 곱해봅니다. 만약 이 곱셈의 결과가 $\text{det}(A) \times I$ (단위행렬)이라면, 원하는 증명을 완료할 수 있습니다.

행렬 $A$와 $\text{adj}(A)$의 곱에서 얻는 특정 위치 $(i, j)$의 원소는 다음과 같습니다:

$(A \cdot \text{adj}(A))_{ij} =\sum_{k=1}^{n} a_{ik} (\text{adj}(A))_{kj} =\sum_{k=1}^{n} a_{ik} C_{jk}$

라플라스 전개에 의하면, $i = j$일때, $\sum_{k=1}^{n} a_{ik} C_{jk}=\sum_{k=1}^{n} a_{ik} C_{ik}=\text{det}(A)$입니다.

만약, $i \ne j$인경우, $\sum_{k=1}^{n} a_{ik} C_{jk}$은 행렬 $A$의 $j$번째 행이 무엇이든 같은 값을 가집니다. 행렬 $B$가 $A$와 $j$번째 행을 제외하고 다 동일하면, $B$에 대해서 $\sum_{k=1}^{n} a_{ik} C_{jk}$을 계산한 것은 $A$에 대해 계산한 것과 같다는 뜻 입니다. $B$의 $j$번째 행을 $A$의 $i$번째 행과 같다고 합시다. (따라서, $b_{ik}=b_{jk}$) 그리고 나머지 모든 행은 $A$와 동일하다고 합시다. 그러면, $\sum_{k=1}^{n} a_{ik} C_{jk}=\sum_{k=1}^{n} b_{ik} C_{jk}=\sum_{k=1}^{n} b_{jk} C_{jk}=\text{det}(B)$이어야 합니다. $B$의 두 행이 같으므로, $\text{det}(B)=0$이고 따라서, $i \ne j$인경우, $\sum_{k=1}^{n} a_{ik} C_{jk}$ 은 0입니다. 결과적으로

$(A \cdot \text{adj}(A))_{ij} =\sum_{k=1}^{n} a_{ik} (\text{adj}(A))_{kj} =\sum_{k=1}^{n} a_{ik} C_{jk}=\text{det}(A) I_{ij}$ 입니다.
따라서, $(A \cdot \text{adj}(A))=\text{det}(A) I$입니다.

몇몇 정리들

우리는 행렬식의 핵심 성질 $\text{det}(AB)=\text{det}(A)\text{det}(B)$를 증명했습니다. 그리고, 행렬식과 역행렬이 직접적으로 연관이 있음을 보여주는 여인수전개와 관련한 정리를 증명했습니다. 아래의 정리들은 따름정리들입니다.

역행렬의 행렬식

행렬 $A$의 역행렬 $A^{-1}$의 행렬식은 원래 행렬 $A$의 행렬식의 역수와 같습니다.

$\text{det}(A^{-1}) = \frac{1}{\text{det}(A)}$

행렬식이 0일 필요충분조건

행렬식의 기본성질 이용한 $\text{det}(AB)=\text{det}(A)\text{det}(B)$의 증명과 Laplace 전개를 통한 행렬식이 Leibniz 공식의 행렬식과 같다는 증명이 전제되면, 행렬이 비가역적일 필요충분조건은 해당 행렬의 행렬식이 0인 것임을 증명하기 매우 쉬워집니다.

가역행렬의 행렬식은 0이 아닙니다

행렬 $A$가 가역행렬이고 그 역행렬을 $A^{-1}$이라 하면, $AA^{-1} = I$입니다.

$det(AA^{-1}) = det(I)=1$이므로, $det(A) \times det(A^{-1}) = 1$입니다.

만약 $det(A) = 0$이라면, $0 \times det(A^{-1}) = 1$이라는 모순이 생깁니다. 따라서, $det(A) \neq 0$이어야 합니다.

행렬식이 0이 아니면, 행렬이 가역행렬입니다:

이전에 한 증명은 행렬의 행렬식이 0일 필요충분조건은 해당 행렬의 행 또는 열이 선형 종속인 것이라는 개념을 사용했으나, 아래의 증명은 그렇지 않습니다.

$\text{det}(A) \neq 0$ 이라면, 행렬 $A$는 가역적입니다. 왜냐하면 역행렬이 $A^{-1} = \frac{1}{\text{det}(A)}\text{adj}(A)$으로 주어지기 때문입니다.

닮은 행렬의 행렬식은 서로 같습니다.

닮은 행렬(similar matrix)이란, 두 행렬 $A$와 $B$가 어떤 가역행렬 $P$에 대해 $B = P^{-1}AP$의 관계를 가질 때 $A$와 $B$를 닮은 행렬이라고 합니다. 그렇다면, 이 두 행렬의 행렬식이 동일하다는 것을 증명해보겠습니다.

$\text{det}(B) = \text{det}(P^{-1}AP)$

$\text{det}(P^{-1}AP) = \text{det}(P^{-1}) \times \text{det}(A) \times \text{det}(P)$

그리고 역행렬의 행렬식 성질에 따라 $\text{det}(P^{-1}) = \frac{1}{\text{det}(P)}$이므로:

$\text{det}(P^{-1}AP) = \frac{1}{\text{det}(P)} \times \text{det}(A) \times \text{det}(P)$

$\Rightarrow \text{det}(B) = \text{det}(A)$

따라서, 두 행렬 $A$와 $B$의 행렬식은 동일하다는 것을 증명하였습니다.

Cramer's Rule:

Cramer의 규칙은 선형 연립방정식의 해를 찾는데 사용되는 공식입니다. $n \times n$ 계수 행렬 $A$와 상수 벡터 $\bold b$로 구성된 선형 연립방정식 $A\bold x = \bold b$에대해, $A$의 행렬식이 $0$이 아닌 경우 (즉, $A$가 가역적인 경우), 각 변수 $x_i$에 대한 해는 다음과 같습니다:

$x_i = \frac{\text{det}(A_i)}{\text{det}(A)}$
여기서 $A_i$는 행렬 $A$에서 $i$번째 열이 벡터 $\bold b$로 대체된 행렬입니다.