Introduction

Information Theory is the way to share idea. Each media has a diffent for consuming time and size of content. For example, sending by letter is takes long time but email is sended instaneously. In addition, telling by dialog uses less energy and effort than by singing. Let's look the definition on wikipedia.

[ Information Theory ]

the scientific study of the quantification, storage, and communication of information.

Modern Information Theory

To sending message by simple machine, symbolize(encoding) the human words or sentence used a lot. Let's consider morse code. It consists only 0 and 1. Each alphabet represent a unique pattern of bynary digits.

Measuring Information

Alice wants to send alphabet "f" to Bob. Alice only send 0 or 1. 0 means left size and 1 means right size. (But on odd numbers, split n+1, n) To do this, Alice has to send 4 messages, 0101. If she wants to send "E", whole messages are 01010.

Therefore this communication needs $2^4$ message space. The 4 messages has binary data. From the point of view, to present 26 kinds of alphabet, $2^? = 26$, $\log_2(26) = 4.7...$. In other words, Alice has to send 4 messages in minimum, 5 messages in maximum.

Through the past, quantitative measure of information is needed. It's done the logarithm of the number of symbol sequences.
$H=n\log s = \log s^n$

Markov Chain

[ Galton Board ]

Binomial Distribution
After trying to flip 10 coins over 10000 times, the situation all coins are front or back occurs lower than mixed. Always almost same distirubtion like the red line in the video.

[ Markov Chain ]

The concept of modeling sequences of random events using states and trasitions between states

Like this, We can assume that all the things or status has a ratio, probability. Markov designed the chain shows probability of every transition between nodes. The probability of transition is the transition matrix.

Transition matrix of the image $= \begin{pmatrix} 0.50 & 0.35 \\ 0.50 & 0.65 \end{pmatrix}$

Information Entropy

Alice sends "ABCABCADCCCC" to Bob. Bob reads the sequence and decodes each letter based on following decision tree.

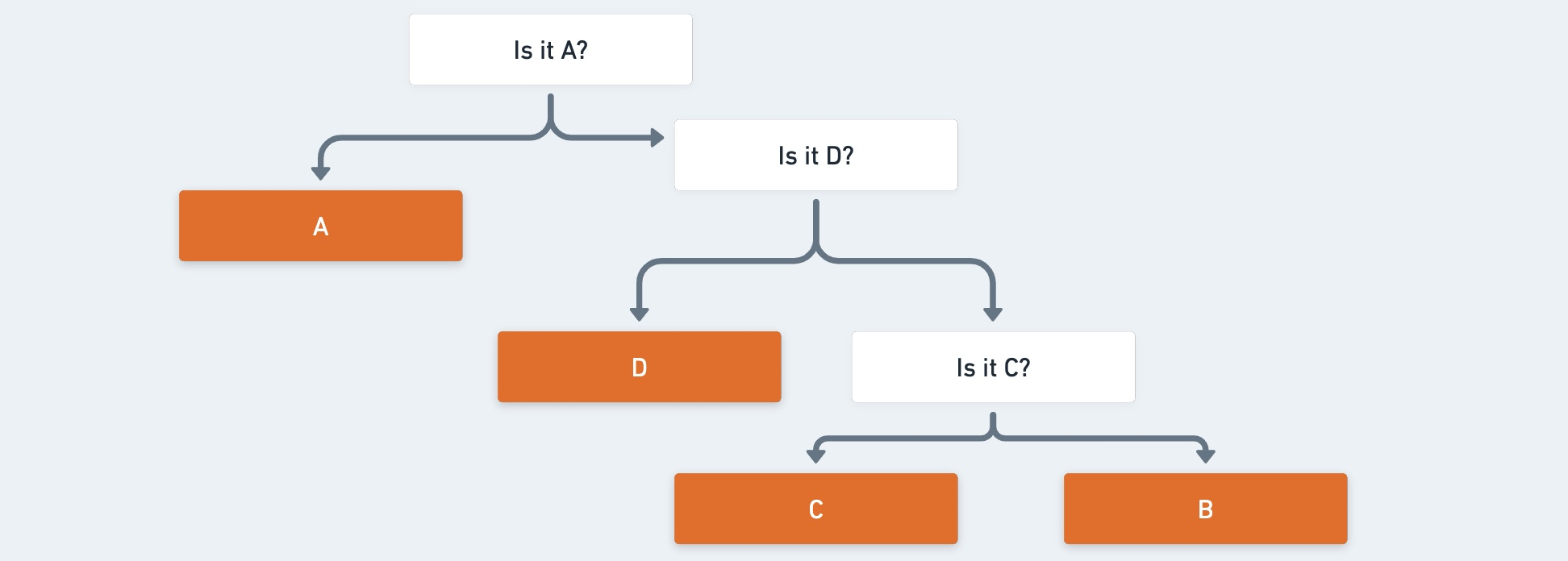
To spend less time to decide alphabet, Bob checks the probability of each alphabet's frequency.

$P(A) = 0.25$ - A passes one question
$P(B) = 0.16$ - B passes three questions
$P(C) = 0.5$ - C passes three questions
$P(D) = 0.08$ - D passes two questions

Therefore the expectation of question per a letter is $0.25\times1 + 0.16\times3 +0.5\times3+0.08\times2 = 2.39$ questions. It's identical to expectation $E[X] = \sum^{\infin}_{i=1}x_ip_i$. It is the generalization of the weighted average of all possible outcomes.

Likewise, the entropy is $H=\sum^n_{i=1}(\{questions\})p_i$. The number of question on each alphabet is the depth in decision tree. And each node has 2 child node, the depth is $\log_2(\{depth\})$. Entropy is $H=\sum^n_{i=1}\log_2(\{outcomes\})p_i$. Now go back to the galton board. The probability that all coins are same side is lower but mixed case has the high probability. Like this, outcomes can be probability of each case and are as called, surprise . Surprise is $\frac{1}{probability}$.

Finally, formula of information entropy is $H=\sum^n_{i=1}\log_2(\frac{1}{p_i})p_i = \sum^n_{i=1}-\log_2(p_i)p_i$
($\log_2(1)$ is zero.)

import math
p = (0.25, 0.16, 0.5, 0.08)
math.fsum( (math.log(1/x) * x for x in p))
# 1.1884185063043353

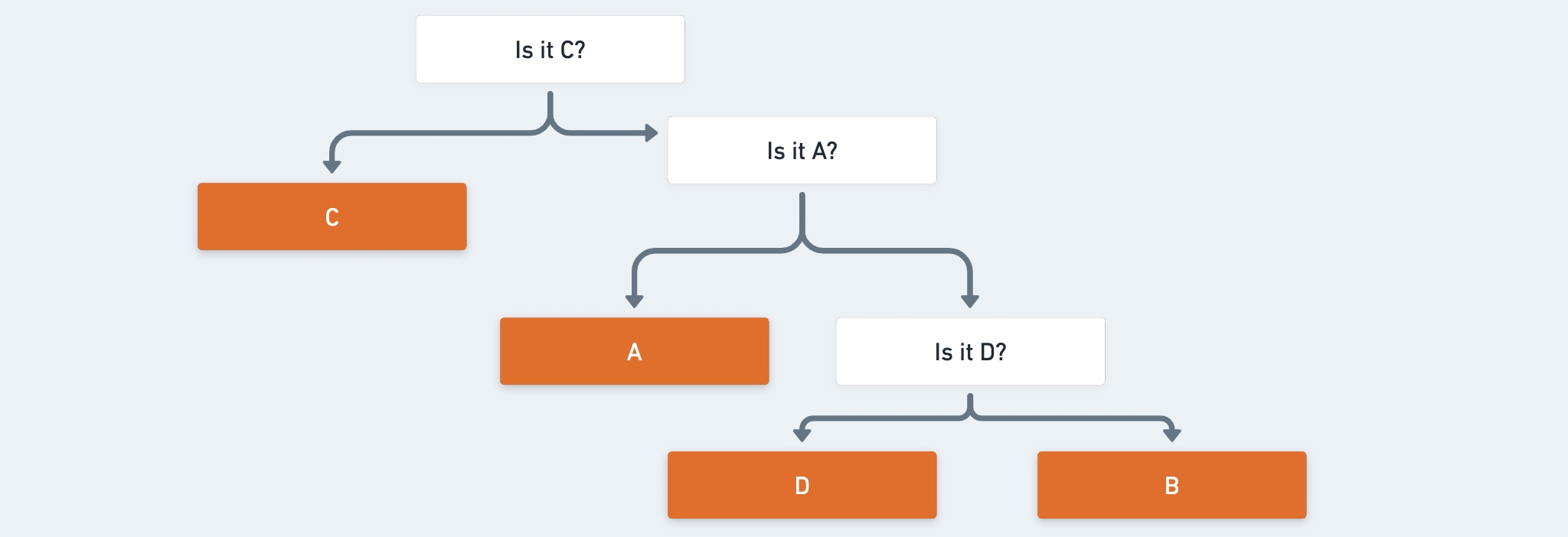
Let's calculate each node. In root node, yes is 25% and no is 75%, as followed, entropy of root node is -0.56. Second node has 16% and 59%, respectively, then entropy of second node is -0.60. Entropy of last node is -0.55.

At the end, Bob revises the decision tree, node which gets higher entropy goes up.

---

Reference

• https://en.wikipedia.org/wiki/Information_theory
• https://en.wikipedia.org/wiki/Expected_value
• https://www.khanacademy.org/computing/computer-science/informationtheory/