Actor-Critic with Softmax Policies

가정: finiate set of action & continuous states

• softmax : $\frac{e^{z_i}}{\Sigma^K_{j=1} e^{z_i}}$
  • guarantee the result of probability is positive and summed to one
• choice for policy parameterization($\theta$) for finite action: by Softmax
  • $\pi(a|s,\theta) := \frac{e^{h( s,a,\theta}}{\Sigma_{b\in A}e^{h(s,b,\theta)}}$

critic은 현재 state에서 오직 하나의 feature vector만 필요하다

• $\nabla \hat v (s,w) = x(s)$ 이므로
• $w \leftarrow w + \alpha^w \delta \nabla \hat v (S,w)$
• 고로 critic's weight update는 alpha * TDR times the feature vector

action은 현재 state와 action에 종속적이기에 state-action feature vector가 필요하다

• $h(s,a,\theta) := \theta^Tx_h(s,a)$
• gradient: $\nabla \ln \pi (a|s,\theta) = x_h(s,a) - \Sigma_h \pi(b|s,\theta) x_h(s,b)$
  • (state-action feature for the selected action) - (state-action feature multiplied by the policy summed over all actions)

Gaussian Policies for Continuous Actions

Gaussian Distribution (=Normal Distribution)

• $f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}$
  • $\mu$ == mean
  • $\sigma$ == variance of the distribution

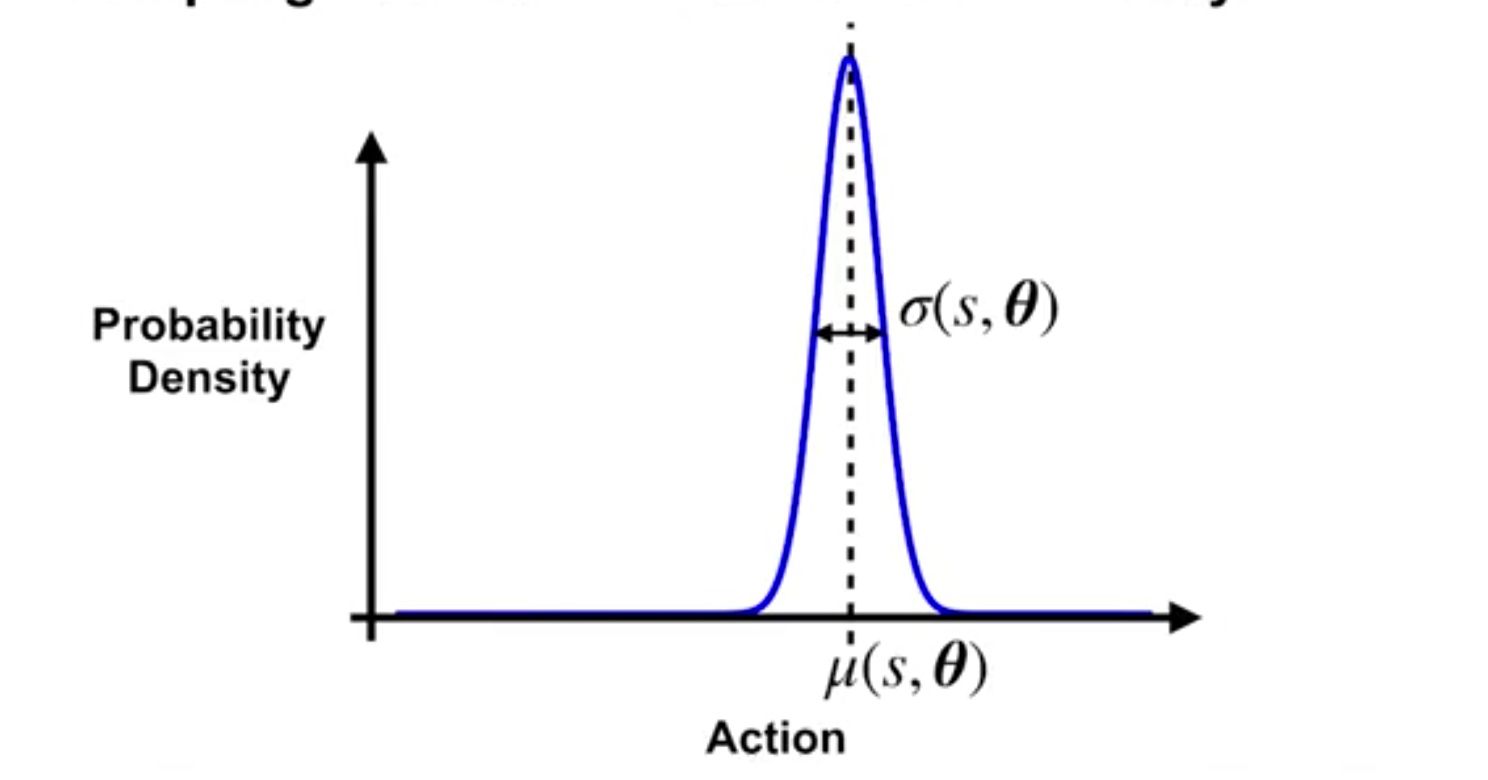
Gaussian policy

• $\pi(a|s,\theta) := \frac{1}{\sigma(s,\theta)\sqrt{2\pi}}\exp(-\frac{(a-\mu(s,\theta))^2}{2\sigma(s,\theta)^2})$
• $\mu(s,\theta) := \theta^T_{\mu}x(s)$
• $\sigma := \exp(\theta^T_{\sigma}x(s))$
• $\theta := \begin{bmatrix} \theta_{\mu} \\\theta_{\sigma} \end{bmatrix}$

action의 범위가 학습이 진행됨에 따라 점점 줄어들면서
각 상태 별 최적의 행동을 선택하게 한다

Gradient of the Log of the Gaussian Policy

• $\nabla \ln \pi(a|s,\theta_{\mu}) = \frac{1}{\sigma(s,\theta)^2}(a-\mu(s,\theta))x(s)$
• $\nabla \ln \pi(a|s,\theta_{\sigma}) = (\frac{(a-\mu(s,\theta))^2}{\sigma(s,\theta)^2}-1) x(s)$