!! 여기서의 Prediction은
주어진 policy를 이용하여 state value function를 학습하는 것이다

Monte Carlo in RL

Monte Carlo에서는
여러 번의 episode를 진행할 경우에
한 episode마다 얻었던 모든 value에 대해 평균을 구한다
더 많은 value가 관측될 수록
그 평균값은 기댓값으로 수렴한다

즉, expected return 대신에
표본집단의 평균 return을 사용한다

RL에서 Monte Carlo의 평균값은
mean이 아닌
incremental mean이다

Incremental Mean

여러 개를 모아놓고 한 번에 평균을 취하는 것이 아니고
하나 하나 더해가며 평균을 계산하기에
incremental mean을 사용

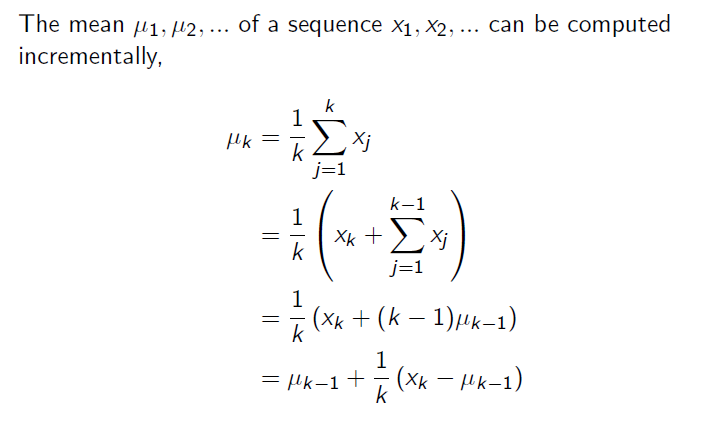
First VS Every Visit MC

만약에 동일한 episode내에서
특정 state를 두 번 방문한다면 어떻게 해야할끼?
두 가지 방법이 있다

policy 𝝅를 따르는 state s의 가치 $v_{\pi}(s)$를 추정하길 원한다고 가정
한 에피소드에서 state s가 발생할 때마다
그것은 s와의 접촉 visit으로 불린다

동일한 episode 안에서 s를 여러 번 마주칠 수 있다

• first-visit MC method는
  s와의 최초 접촉 이후에 발생하는 이득의 평균을 구함으로써
  $v_{\pi}(s)$를 추정한다

반면에

• every-visit MC method는
  s와의 모든 접촉 이후에 발생하는 이득의 평균을 구한다

둘 다 s와의 접촉 또는 최초 접촉의 개수가 무한으로 갈 수록
$v_{\pi}(s)$로 수렴한다

Incremental Monte-Carlo Update

에피소드가 끝나고 V(s)를 갱신한다
이 때 각 state $S_t$마다 반환값으로 목표 $G_t$를 얻게 된다

• $N(S_t)$ ← $N(S_t) + 1$
• $V(S_t)$ ← $V(S_t) + \frac{1}{N(S_t)}\underbrace{(G_t - V(S_t)^{error})}$
  • $\frac{1}{N(S_t)}$ : error가 향하는 방향으로 얼만큼 이동시킬지 결정

non-stationary problem에서는
구하고 있는 평균을 추적하는 것이 도움이 된다
즉, 과거의 에피소드를 잊어버린다

• $V(S_t) ← V(S_t) + α (G_t − V(S_t))$

stationary problem이란
시간이 흘러감에 따라 기존의 값이 유지되는 것을 의미하고
non-stationary problem이란
시간이 흘러감에 따라 값이 달라지는 상황을 의미한다

Bootstrap과 Sampling

Bootstrapping: 추정값으로부터 갱신한다

• ex) DP, TD
• 매 t마다 이전(t-1)의 value function에 저장한 추정값을 이용하여 현재 state의 value를 구한다
• 실제 return 값을 사용하지 않고 추정값을 target처럼 사용한다

Sampling: 기댓값의 표본들을 추출하여 갱신한다

• ex) MC, TD

Bootstrap

모든 DP 방법은
어떤 state의 value 추정값을 갱신할 때,
그 state로부터 파생되는 state의 value 추정값을 기반으로 한다

다시 말해, 다른 추정값을 기반으로 해당 추정값을 갱신한다

예시로,
이후에 보게 될 SARSA 갱신 방정식을 보면 다음과 같다

• 𝑄(𝑠,𝑎) ← 𝑄(𝑠,𝑎) + 𝛼 ($𝑅_{𝑡+1}$ + 𝛾 𝑄(𝑠′,𝑎′) − 𝑄(𝑠,𝑎))
  Q(s,a)를 구하는데 Q(s,a)만이 아니라 Q(s',a')도 필요하다

단점은
starting value에 따라 bias가 발생한다

Monte Carlo와 DP의 차이

Monte Calro 방법에는 Bootstrap을 하지 않는다

• 𝑄(𝑠,𝑎) ← 𝑄(𝑠,𝑎) + 𝛼 (𝐺𝑡 − 𝑄(𝑠,𝑎))

state 하나의 value를 추정하기 위한 계산이
state 개수와 무관하다

덕분에 오직 하나 또는 일부 state에 대해서만
value를 추정하려고 할 때
DP보단 MC를 먼저 고려해볼 수 있다

관심 있는 state들로 많은 표본 episode를 만들고
다른 state는 제외한 채
선택한 state들에 대해서만 value의 평균을 계산한다

---

출처

• https://dnddnjs.gitbooks.io/rl/content/DP%20example.html
• https://datascience.stackexchange.com/questions/26938/what-exactly-is-bootstrapping-in-reinforcement-learning
• https://www.slideshare.net/carpedm20/reinforcement-learning-an-introduction-64037079