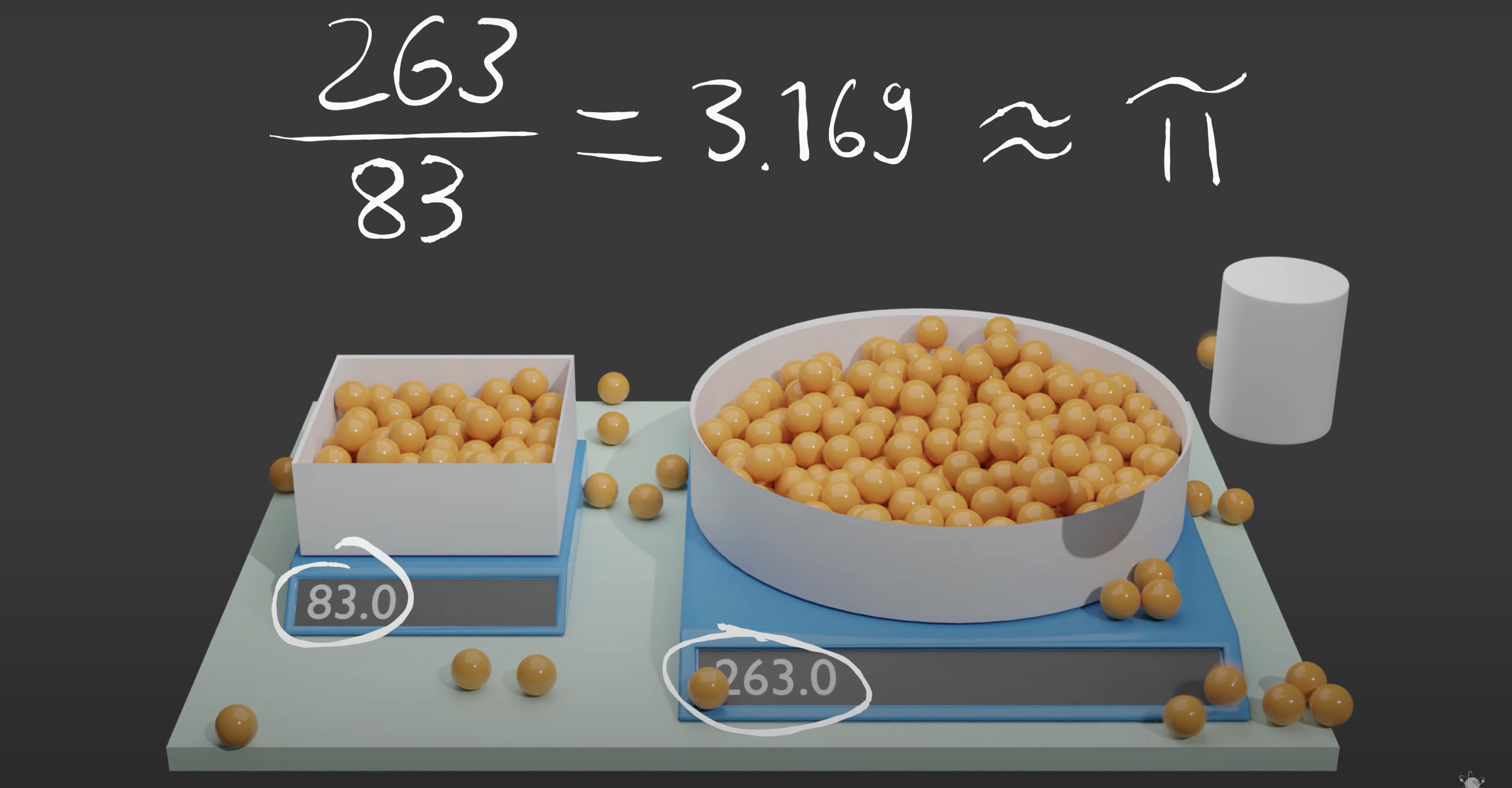실제 이득에 대한 많은 수의 무작위 표본으로부터 평균을 계산할 수 있다

예로 모든 사람의 평균 키를 구해야한다고 할 때,
모든 사람의 키를 아는 것은 어렵다
무작위로 몇 사람을 뽑아서 측정하여 추정해볼 수 있다

---

원주율도 이 방법을 이용해서 구해볼 수 있다

왼쪽 직사각형의 한 변의 길이와
같은 길이의 반지름을 가진 원을 준비한다

이 위로 무작위 위치에서 공을 떨어뜨려
담긴 공의 개수를 측정한다

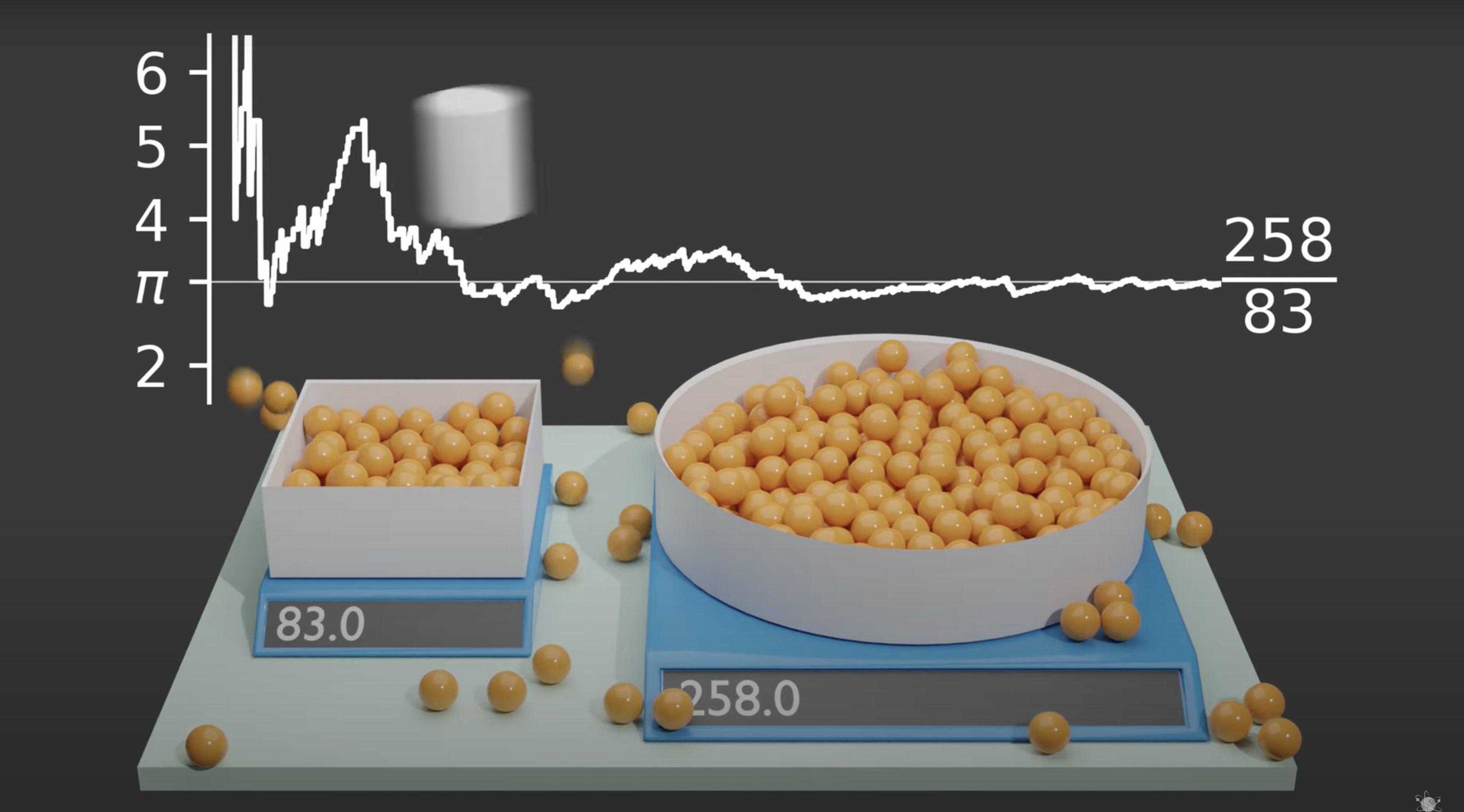
모든 위치를 다 탐색해보는 것은 힘들다
이러한 방식으로 모든 탐색을 다 시도해보는 건
Dynamic Programming이다
다 해본다는 것은 그 경우의 수가 적을 때는 괜찮지만
이처럼 수만가지가 될 때는 시간이 오래 걸린다

그래서 Monte Carlo 방법을 통해
무작위 위치를 선정하여 시도한다

• 
• 

공이 담긴 개수를 비교해보며
그 둘의 넓이의 차이에 대한 비율을 알아볼 수 있었고
이는 원주율과 비슷하다

맨 처음 사진처럼
이 과정을 지속하여도
원주율과 비슷한 숫자로 수렴한다

• 

출처 : https://www.youtube.com/watch?v=7ESK5SaP-bc

---

Monte Carlo Algorithms in RL

model 없이도 강화학습을 하기 위해
경험들의 samples (표본집단)을 이용한다

MDP에 대한 지식이 필요하지 않고, 오직 samples만 있으면 되기에
MC는 model-free

Introduction Function Approximation

Approximation

아래 예시는
1번 그림) 100개의 데이터가 없어진 원본 데이터에서
2번 그림) 표본 집단의 추정값들에 대한 함수를 바탕으로 하여
3번 그림) 원본의 모습을 유추하고 있다

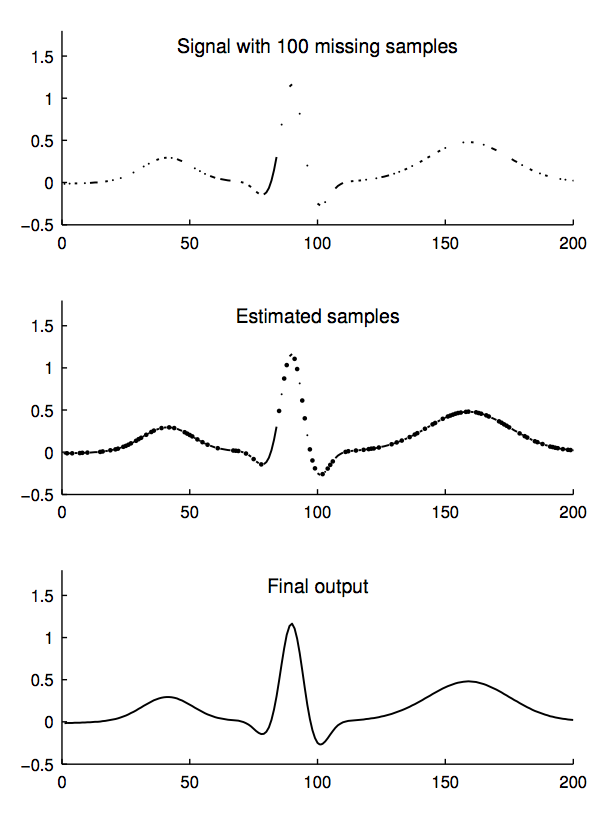
고로
data들의 경향성을 함수화/그래프화 시켜
실제값을 근사하여 알아내는 방식을 쓸 것이다

Value Function Approximation

지금까지 살펴본 것은 열람표(lookup table)이다

• 모든 state s는 한 칸의 v(s)를 가진다
• 또는 모든 state-action s,a pair는 한 칸의 q(s,a)를 가진다

여기서 문제는 MDP가 거대할 때

• 너무 많은 state와 action을 메모리에 저장하기 어렵고
• 학습이 굉장히 느려지며
• 개개별의 state가 완벽히 관찰되지 않을 수 있다

그래서 value function 추정을 function approximation을 이용하여 해볼 수 있다

• $v_w(s) ≈ v_{\pi}(s)$
• $q_w(s,a) ≈ q_{\pi}(s,a)$

parameter w를 갱신함으로써
보지 못한 states를 일반화한다

agent state update

이 때 parameter w를 가지며 사용 되는 agent state는 다음과 같다

• $S_t = u_w(S_{t-1}, A_{t-1}, O_t)$

아무튼 이런 게 있고
지금은 여기서 더 이상 다루지 않는다

Linear Function Approximation

Feature vector

머신러닝에서의 feature vector는 다음과 같다
각 특성을 일렬로 나열한 1차원 벡터로 볼 수 있다

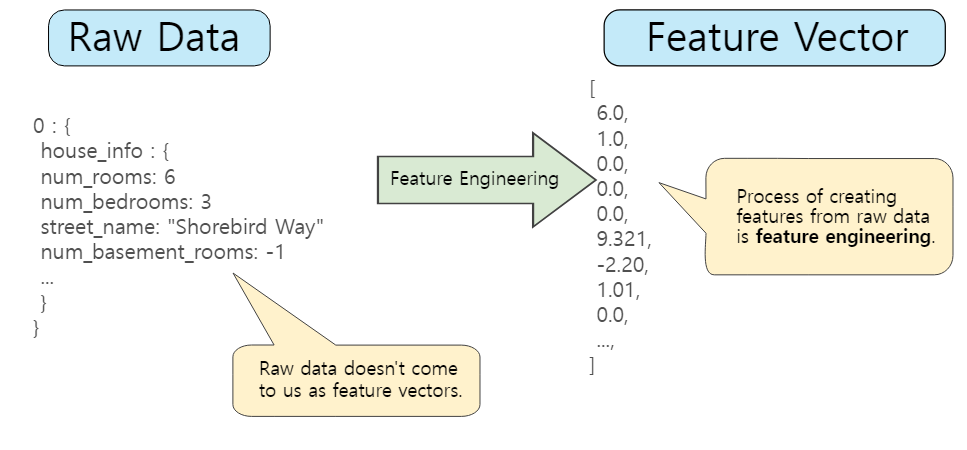
one-hot encdoing을 이용해
하나의 vector로 하나의 feature를 표현하기도 한다

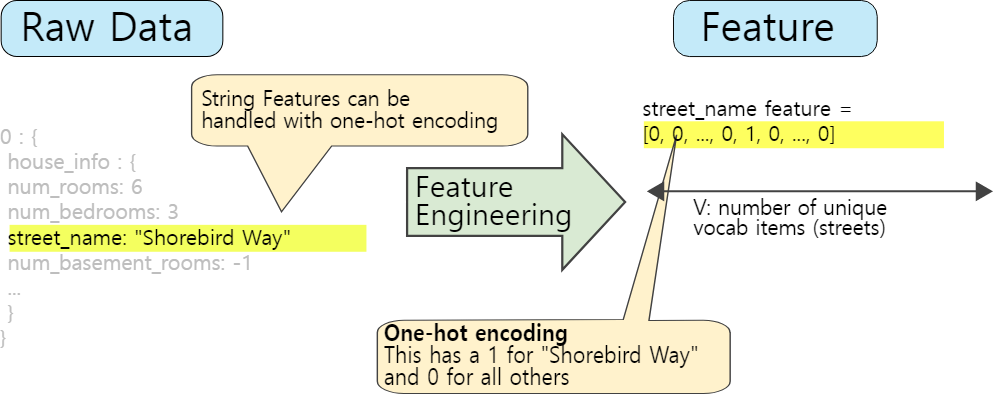
RL에서는 state를 feature vector로 표현한다

• 
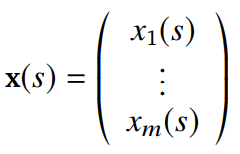
• 간단하게 표현한다면 : $x_t = x(S_t)$
  이 때의 S_t는 agent state update의 식을 따른다

예시로
I Distance of robot from landmarks
I Trends in the stock market
I Piece and pawn configurations in chess

Linear Value Function Approximation

이렇게 features의 선형적인/일차원의 조합을 이용하여
value function의 근사치를 구할 수 있다

• $v_w(s) = w^Tx(s) = \sum^n_{j=1}x_j(s)w_j$

loss function인 Objective function은
w에 대한 2차 방정식으로 표현된다

• $L(w) = E_{S~d}[(v_{\pi}(S) - w^Tx(s))^2]$

Stocahstic gradient descent는
global optimum으로 수렴한다

갱신 규칙은 다음과 같다

• update = step-size x prediction-error x feature-vector
  • $\nabla_wv_w(S_t) = x(St) = x_t$
  • $\Delta w= \alpha(v_{\pi}(S_t) - v_w(S_t)) * x_t$

Table Lookup Features

열람표(table lookup)은
one-hot feature를 의미한다

n개의 states가 $S = {s_1, ... s_n}$라면
이 때의 one-hot feature는

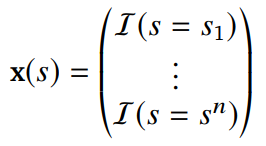
parameter w는 각 state의 value 추정치를 포함한다
$v_w(s) = w^Tx(s) = \sum^n_{j=1}x_j(s)w_j$

---

출처

• https://developers.google.com/machine-learning/crash-course/representation/feature-engineering
• https://eeweb.engineering.nyu.edu/iselesni/lecture_notes/least_squares/index.html