Softmax Policy Parameterization

policy를 만드는데 action value를 사용하지 말고
function approximation을 통해 policy를 학습하고 나타내려고 한다

• $\pi$: parameterized policy
  • output the probability of taking that action in that state
• $\theta$: policy parameter vector
• $W$: approximate value function

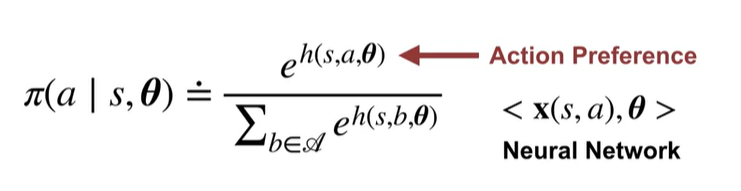
policy에서 선형 함수가 모든 행동에 대한 확률의 합이 1이라고 보장하는 것으 쉽지 않기에
softmax로 각 행동이 0~1 사이의 확률을 가지도록 변환
이를 통해 negative action에서도 non-zero probability를 가지도록 할 수 있다.

action preference는 state, action, $\theta$에 대한 함수

• higher preference == that action is more likely to be selected

다만 action preference와 action value을 혼동하지 말자

• preference == how much the agent prefers each action
• action value == is about summaries of future reward
  

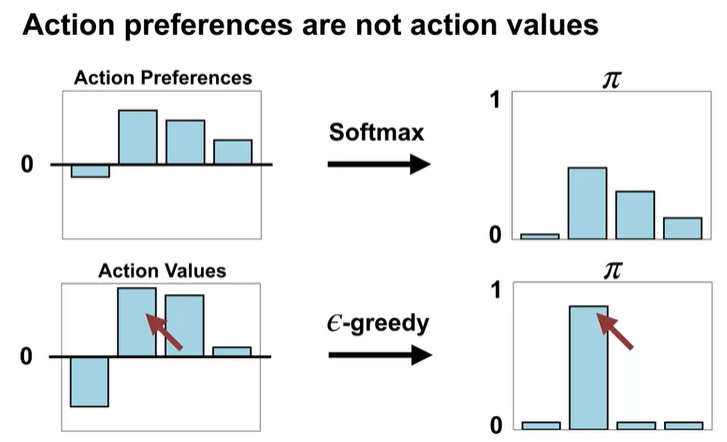
Advantages of Policy Parameterization

Parameterized stochastic policies are useful, because ...

• They can autonomously decrease exploration over time
• They can avoid failures due to deterministic polices with limited function approximation
• Sometimes the policy is less complicated than the value function

Policy Gradient for Continuing Tasks

Using the average reward as an objective for policy optimization

Formalizing the Goal as an Objective

• Episodic: $G_t = \Sigma^T_{t=0}R_t$
• Continuing
  • $G_t = \Sigma^{\infin}_{t=0}\gamma^tR_t$
  • $G_t = \Sigma^{\infin}_{t=0}R_t-r(\pi)$

The Average Reward Objective

• $r(\pi) = \Sigma_s\mu(s) \ \ \Sigma \pi(a|s,\theta) \ \ \Sigma_{s',r}p(s',r|s,a)r$
  • $\Sigma_{s',r}p(s',r|s,a)r \ \rightarrow E[R_t|S_t = s, A_t = a]$
    • state S에서 A라는 action을 취했을 때의 expected reward
  • $\Sigma \pi(a|s,\theta) \ \ \Sigma_{s',r}p(s',r|s,a)r \ \rightarrow E_{\pi}[R_t|S_t=s]$
    • all possible actions weighted by their probability under $\pi$
    • It returns the expected reward under the policy $\pi$ from a particular state S
  • $\Sigma_s\mu(s) \ \ \Sigma \pi(a|s,\theta) \ \ \Sigma_{s',r}p(s',r|s,a)r \ \rightarrow E_{\pi}[R_t]$
    • It returns the overall average reward by considering the fraction of time we spend in state S under policy $\pi$

Policy Gradient

Learning policy directly!

Before we were minimizing the mean squared value error,
Now we are maximizing an objective

That means we will want to move in the direction of the (positive) gradient rather than the negative gradient

Understanding $\Sigma_a\nabla\pi(a|s,\theta)q_{\pi}(s,a)$

up & left action have negative value
down & right action have positive value

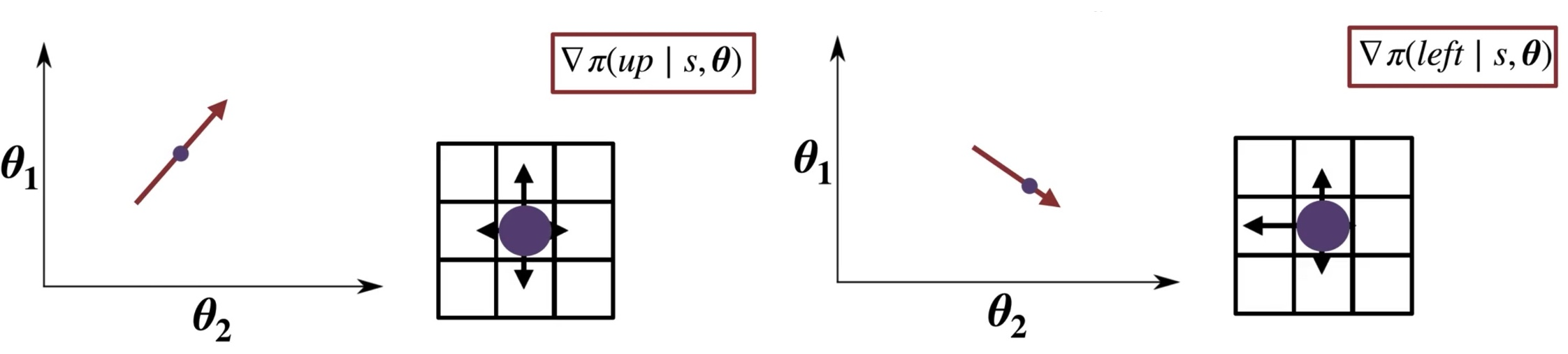
Policy gradient theorem의 the overall average reward를 증가시키는 direction을 찾는 방법에 대하 설명하자면 다음과 같다.

weighted sum은 direction을 알려주는데 그림처럼 우측 하단에 목표가 위치된 경우라면 down & left에 positive를 최대화하고, up & right에 negative를 최소화하는 식으로 진행된다.