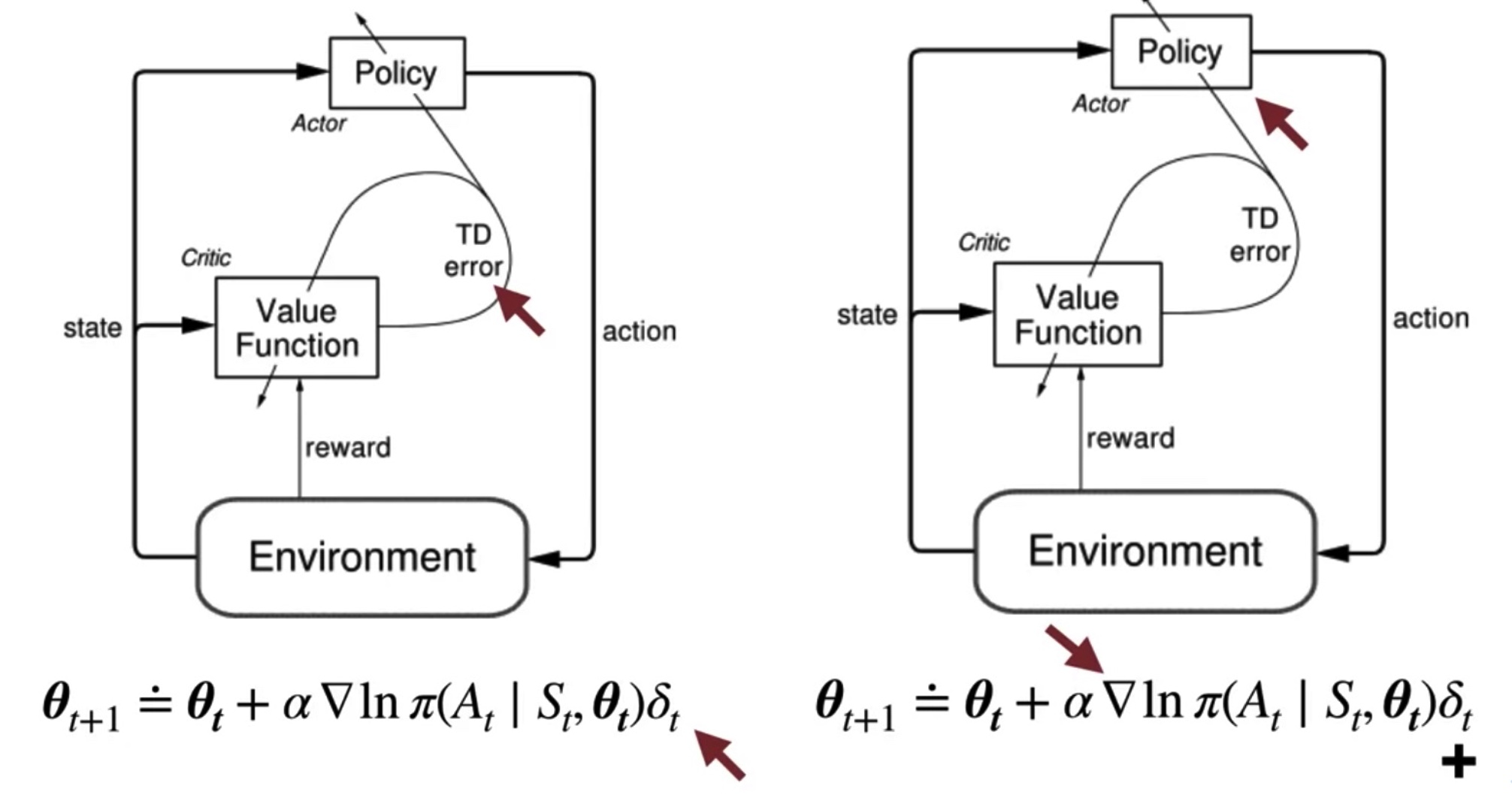
Estimating the Policy Gradient

We have to get the stocastic probability of gradient
Consider stocastic probability as non-biased estimates

Because Sum of states is impractical, Get rid of it

$\Sigma_a \nabla \pi(a|S,\theta) q_{\pi}(S,a)$

• $=\Sigma_a \pi(a|S,\theta) \frac{1}{\pi(a|S,\theta)} \nabla \pi(a|S,\theta) q_{\pi}(S,a)$
• $\rightarrow E_{\pi} [\frac{\nabla\pi(A|S,\theta) }{\pi(A|S,\theta) }q_{\pi}(S,A)$

그래서 update rule은 다음과 같다.
즉 주어진 state와 action에 대한 stocastic probablity gradient를 계산하는 방법이다
$\theta_{t+1} := \theta_t + \alpha \nabla \ln_{\pi}(A_t|S_t,\theta_t) q_{\pi}(S_t,A_t)$

• Gradient of the policy: $\nabla \ln_{\pi}(A_t|S_t,\theta_t)$
  • 이미 policy와 parameterization을 알고 있기 때문에 gradient를 쉽게 계산할 수 있다.
• Estimate of the differential values: $q_{\pi}(S_t,A_t)$
  • action value는 다양한 방식으로 추정할 수 있는데, 예로 differential action values를 학습하는 TD 알고리즘을 사용해볼 수 있다.
• log를 사용하는 이유: 0~1 사이의 확률을 0~$\infin$ 사이로 변환하기 위해. 이를 통해 아주 큰 확률을 크게 표현할 수 있게 된다. 더불어 log를 사용하면 log 간 곱셈이 덧셈으로 치환되기에 이러한 이유에서 log를 사용한다.

Actor-Critic Algorithm

Actor-Critic Algorithm은 TD 기반

• actor == parameterized policy
  • change policy to exceed the critics expectation
    • update the policy parameters
  • use TDR from critic: $\theta \leftarrow \theta + \alpha^{\theta} \delta \nabla \ln \pi (A|S,\theta)$
• critic == value function
  • (evaluating the actions selected by the actor)
  • update its value function to evalute actions selected by the actor(policy)
  • semi-gradient TD 기반: $w \leftarrow w + a^w \delta \nabla \hat v (S,w)$

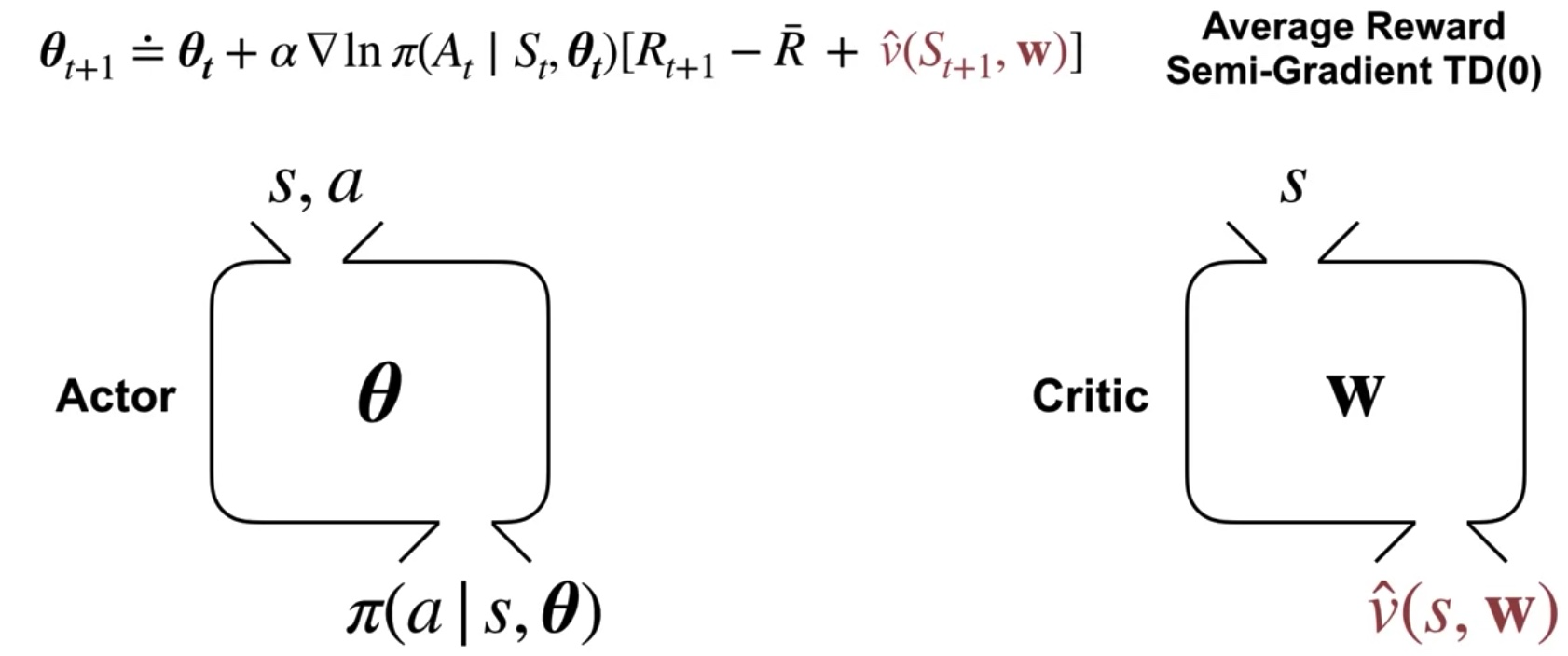
Approximating the Action Value in the Policy Update

Subtracting the Current State's Value Estimate

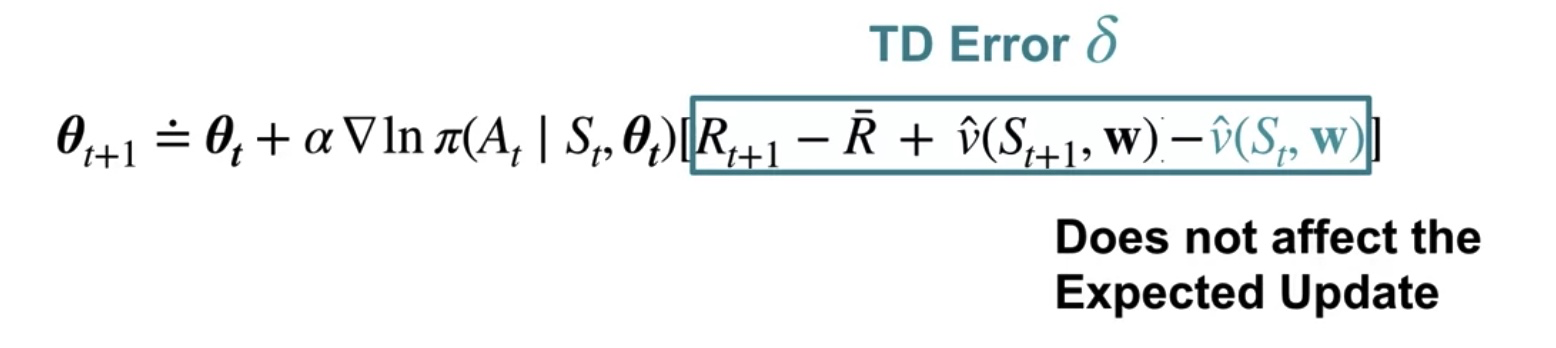
How the Actor and the Critic Interact

$\theta_{t+1} := \theta_t + \alpha \nabla \ln \pi(A_t|S_t,\theta_t) \delta_t$

TD error is positive == selected action resulted in a higher value than expected

By updating, policy parameter changes to increase the probability of actions that were better than expected according to the critic

If the critic is disappointed and the TD error is negative,
then the probability of the action is decreased.

The actor and critic learn at the same time, constantly interacting