
Monte Carlo와 Dynamic programming의 결합
model-free
예측 문제 즉, 주어진 policy 에 대해 value function 를 추정
제어 문제 즉, 최적 정책을 찾기 위해 DP, MC, TD 방법이 모두 GPI를 일부 변형한 형태로 사용한다.
Prediction: MC & TD
여기서 prediction은
policy 하에서 경험한 를 학습한다고 하자
(는 작은 step의 크기/간격을 의미한다)
- Monte-Carlo
- (Incremental every-visit), (stationary MC)
- 갱신한 value 는 표본집단의 반환값인 를 향한다
- Temporal Difference
- (TD(0))
- 갱신한 value 는 표본집단의 반환값인 를 향한다
MC의 단점을 보완한 TD
이 계산을 하려면
이전의 모든 보상값들을 다 알아야 한다
그래서 Monte Carlo의 단점은
한 에피소드가 끝날 때까지 기다려야 한다는 점이다
이를 개선하기 위해
Temporal Difference는
대신 를 사용한다
여기서는 reward를 하나만 얻고
그간 누적된 값을 에서 가져오기에
끝까지 기다리지 않아도 된다
Backup Diagram
DP, MC, TD의 backup diagram을 이해하기 위해
backup diagram을 설명해보자면,
backup (보강)이란
next_state (or state_action_pairs)의 value를
현재 state (or state_action_pairs)에게
전이/대입하는 것이다
Backup Diagram 구성
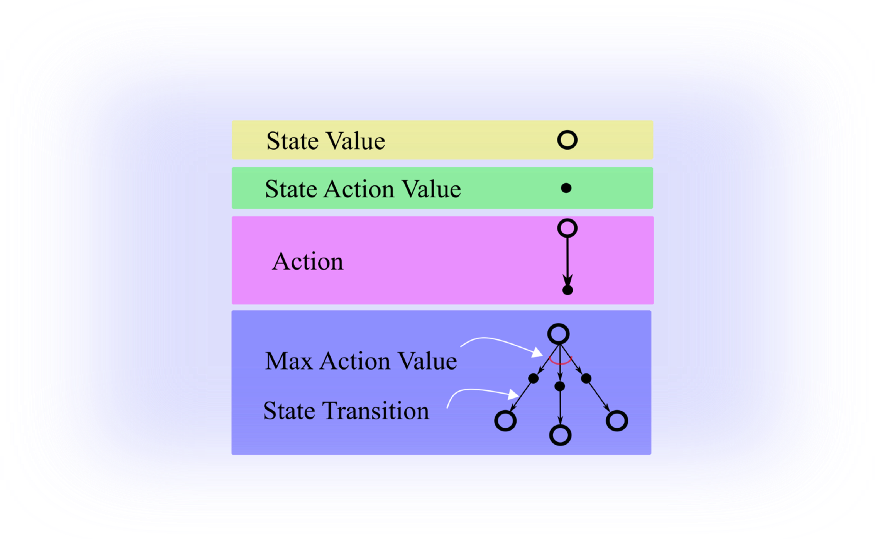
backup diagram의 요소는 다음과 같다
사진 속 max action value는 optimal action을 의미한다
state transition은 state transition probability 를 의미한다
여기에는 없지만 만약 말단 node가
원이 아닌 직사각형이라면
terminal state를 의미한다.
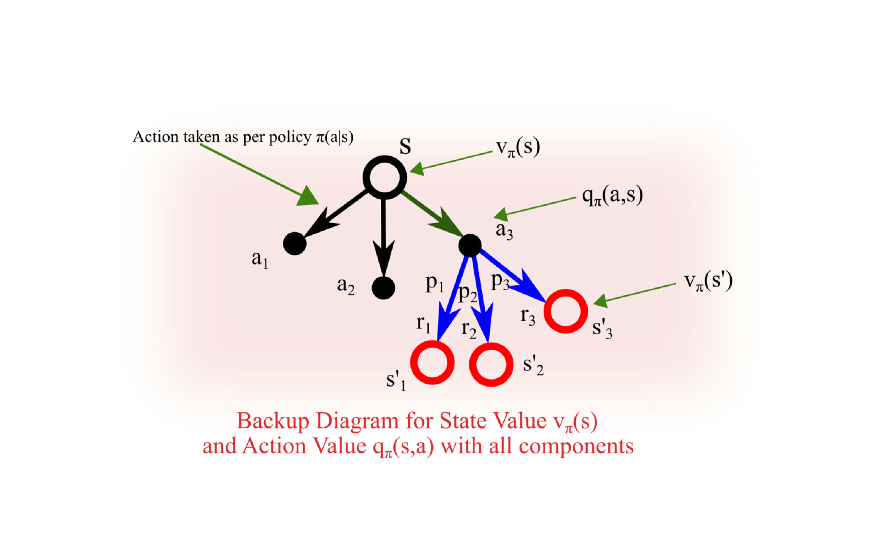
backup diagram 예시.
색상이 모두 검정색이어야 하는데 이해를 돕기 위해 다르게 색칠됐다
1. (큰 흰색 원) - 각 state는
2. (초록 화살표) - policy 가 구한 각 action의 확률값을 기반으로 action을 선택한다
3. (작은 검정색 원) - 그 action을 행하고
4. (파란 화살표) - 이로 인해 다음 state로 넘어갈 확률에 따라
5. (큰 빨간색 원) - 결정된 state로 진행한다
(위에서 본 optimal action에 대한 표기가 없다.
이 예시로 하나 들자면, policy가 epsilon-greedy를 기반할 경우
대부분 optimal action으로 가지만 때때로 무작위로 선택한다)
비교
Dynamic Programming
한 step 앞을 내다보지만, 그중 일부 state가 아닌
가능성이 있는 모든 next_state에 대해서 알아본다
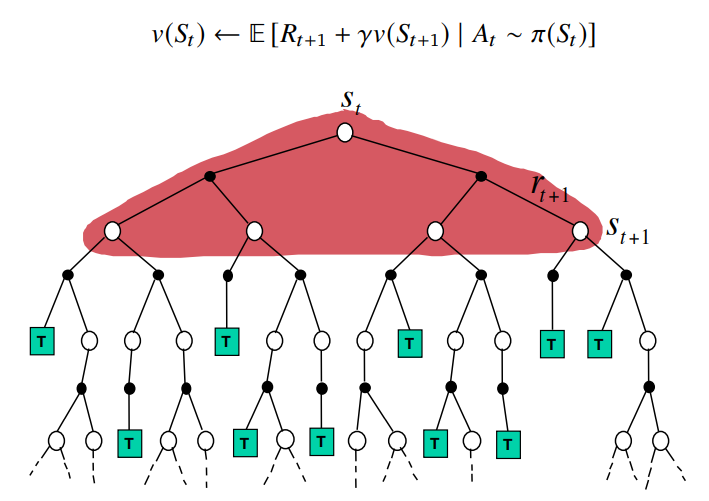
Monte Carlo
끝까지 진행한 궤적 trajectory의 표본만 바라본다
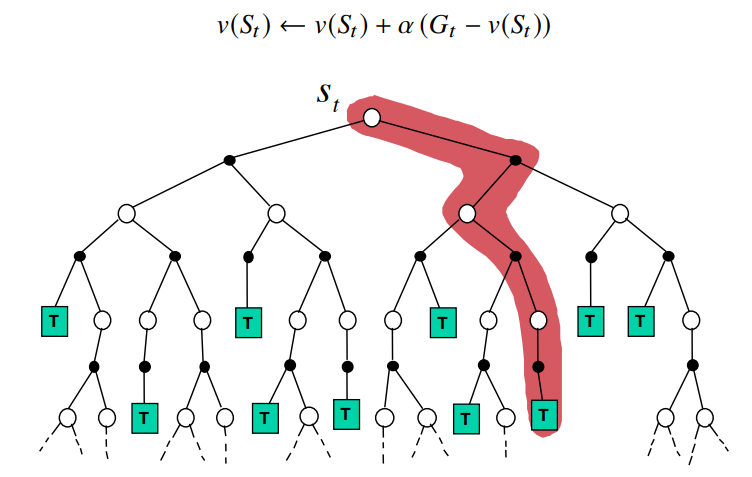
Temporal Difference
sampling을 통해 하나의 action을 선택한 뒤
한 step 앞만 내다본다
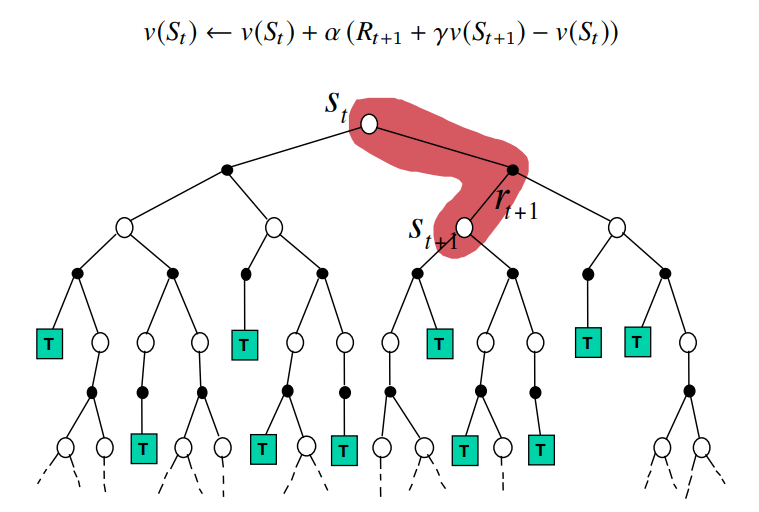
정리
위의 사진들의 붉은색으로 색칠된 부분,
즉 실제 연산이 이루어지는 알고리즘의 방식만 표현하면 아래와 같다
(exhaustive search는 모든 가능성에 대해 처음부터 끝까지 일일이 짚어가며 다 해보겠다라는 것)
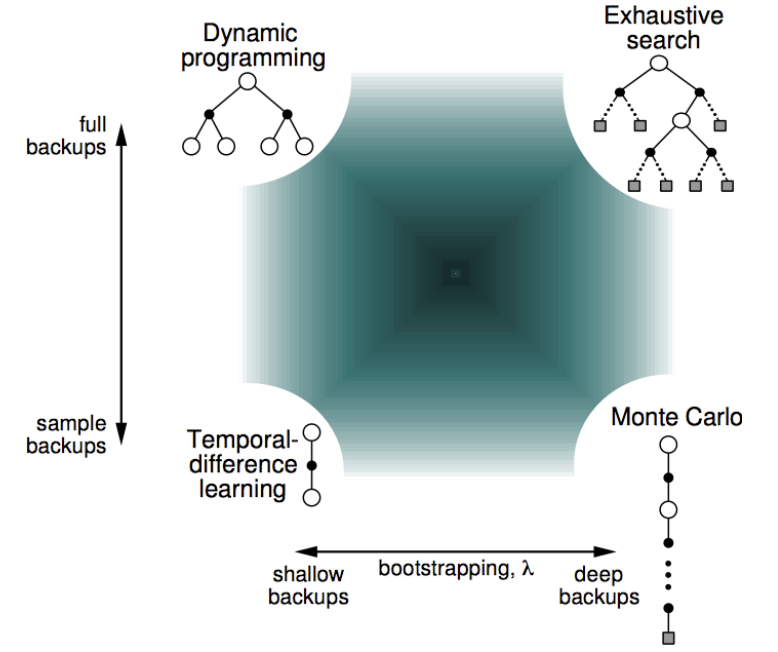
+) backed-up value
+) sample update == update in TD or MC
!= DP의 기댓값 갱신
모든 가능한 상태의 완전한 분포보단, 이후상태의 단일 표본을 기반해야 함
출처
