Temporal Difference: Pred

예측 문제를 풀기 위해 경험을 활용

두 방법 모두,
policy $v_{\pi}$를 따르는 어떤 경험이 주어졌을 때,
그 경험에서 발생한 비종단 상태 $S_t$에 대해
$v_{\pi}$의 추정값 $V$를 갱신한다

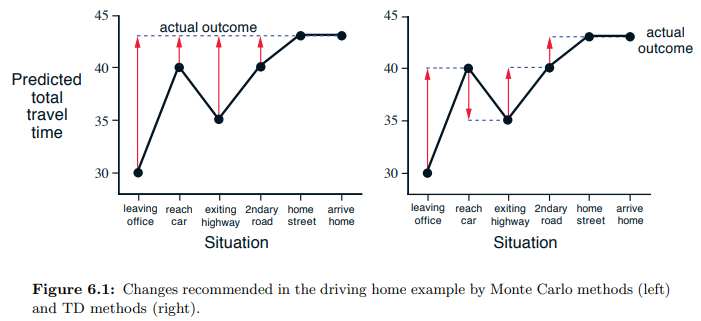
Stationary ${\alpha}$ MC

에피소드가 끝나야만 $G_t$를 알 수 있다

• $V(S_t) ← V(S_t) + {\alpha}(G_t - V(S_t))$
  • $G_t$: 시각 t 이후의 실제 이득
  • ${\alpha}$: 고정 시간 간격 파라미터

TD(0) : 단일 단계(One-step)

다음 시간 단계까지만 기다리면 된다

시각 t+1에서 즉각적으로 목표를 형성하고,
관측된 reward $R_{t+1}$과 추정값 $V(S_{t+1})$을 이용하여 갱신 수행

• $V(S_t) ← V(S_t) + {\alpha}[R_{t+1} + {\gamma}V(S_{t+1}) - V(S_t)]$

부분적으로 이미 존재하는 추정값을 기반으로 갱신되기에, bootstrap 방법이다
TD 방법은 Monte Carlo의 표본추출과 DP의 bootstrap을 결합한다

• $v_{\pi}$ =
  • Monte Carlo: $E_{\pi}[G_t |S_t=s]$
    • 실제 value의 기댓값을 알 수 업식에 표본의 value를 사용
  • DP: $E_{\pi}[R_{t+1}+{\gamma}G_t |S_t=s]$
    • 기댓값이 환경의 model로부터 완전히 제공된다고 가정하므로 기댓값은 알지만
      $v_{\pi}(S_{t+1})$이 알려져 있지 않기 때문에
      대신 현재 추정값 $V(S_{t+1})$이 사용된다

Optimality of TD(0)

batch updating

• 이용 가능한 경험과 에피소드가 유한할 때 점증적으로 수렴하는데, 가치함수의 근사값 V는 모든 비종단 상태에서 계산되지만 변화 횟수는 증가량의 총합만큼 단 한 번이다.
• 그 후 모든 이용 가능한 경험이 새로운 가치함수와 다시 처리되어 새로운 전체 증가량을 만들어내고
• 이 과정은 가치함수가 수렴할 때까지 계속된다
• 즉, - 학습 데이터에 대한 각각의 batch 처리 이후에 갱신이 수행됨

maximum-likelihood estimate

• 데이터를 생성할 확률이 가장 큰 파라미터 값

certainty-equicalence estimate
진행되는 과정의 추정값이 근사값이 아닌 확실히 알려졌음을 가정

TD(0)가 MC보다 더 빨리 수렴하는 이유

• MC는 mse 최소화하는 추정값을, TD(0)는 MDP의 maximum-likelihood estimate에 대해 올바른 추정값을 찾는다
• 일반적으로, TD(0)는 certainty-equivalence estimate로 수렴하기에 MC보다 빠를 수 있다. 더 좋은 추정값으로 이동해서.