Semi-Gradient TD for Policy Evaluation

TD update for function approximation

$U_t$ = TD target

만약$U_t$가 unbiased estimate of true value라면
그 function approximator는 적절한 조건 하에 local optimum으로 수렴한다
더 나아가 $U_t$를 1-step TD처럼 bootstrap target으로 대체할 수 있다.
그러나 TD의 추정값을 사용하는 방식으로 인해 biased 될 수 밖에 없다.

Semi-Grandient TD

원래 TD는 squared error에 대해 gradient descent update를 하지 않기에
이를 semi-greadient method라고 부른다.

Comparing TD and MC with Stdate Aggregation

TD converges to a baised value estimate :(

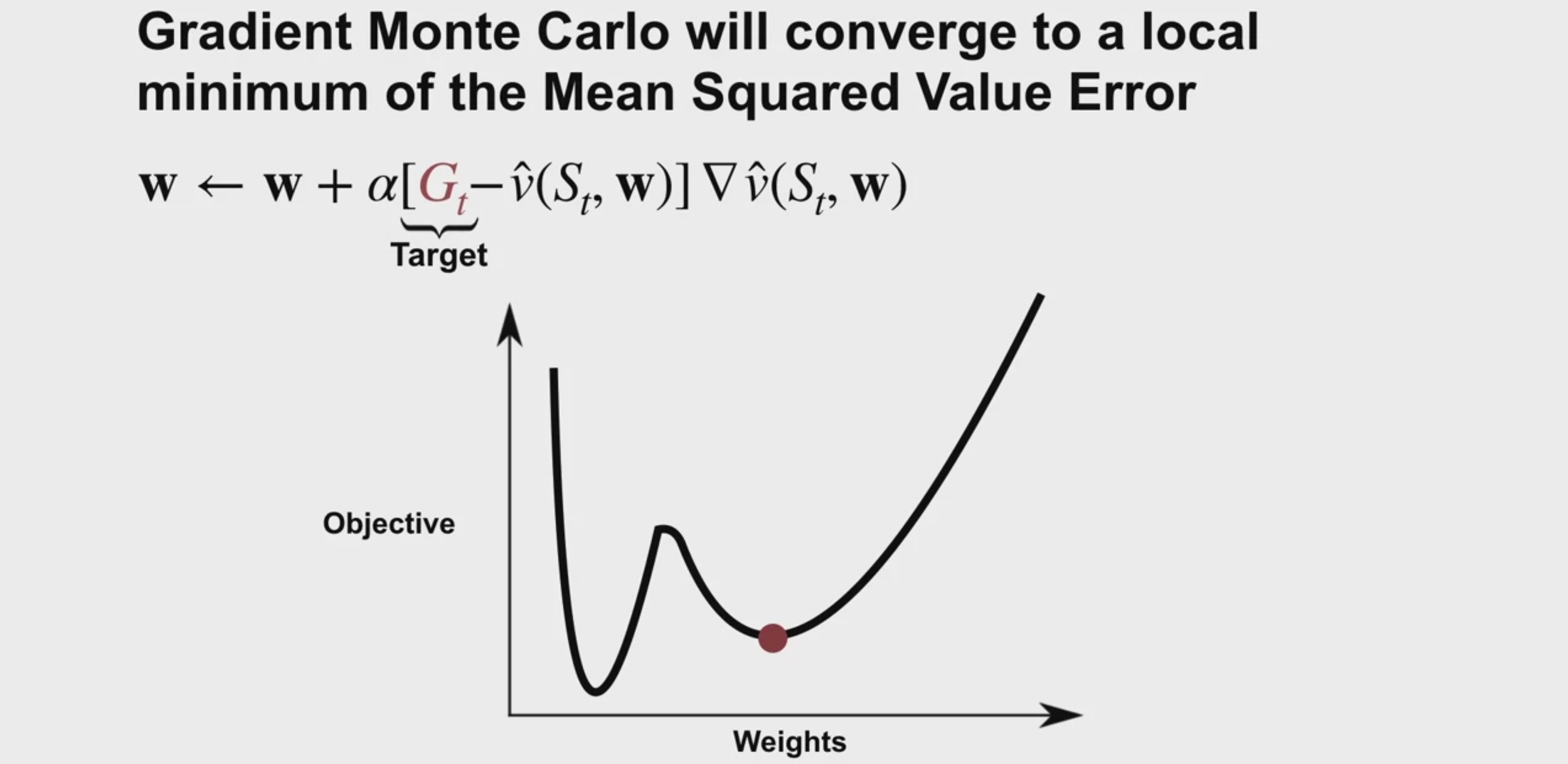
Gradient MC는 끝까지 다 보니까 local minimum으로 수렴하지만
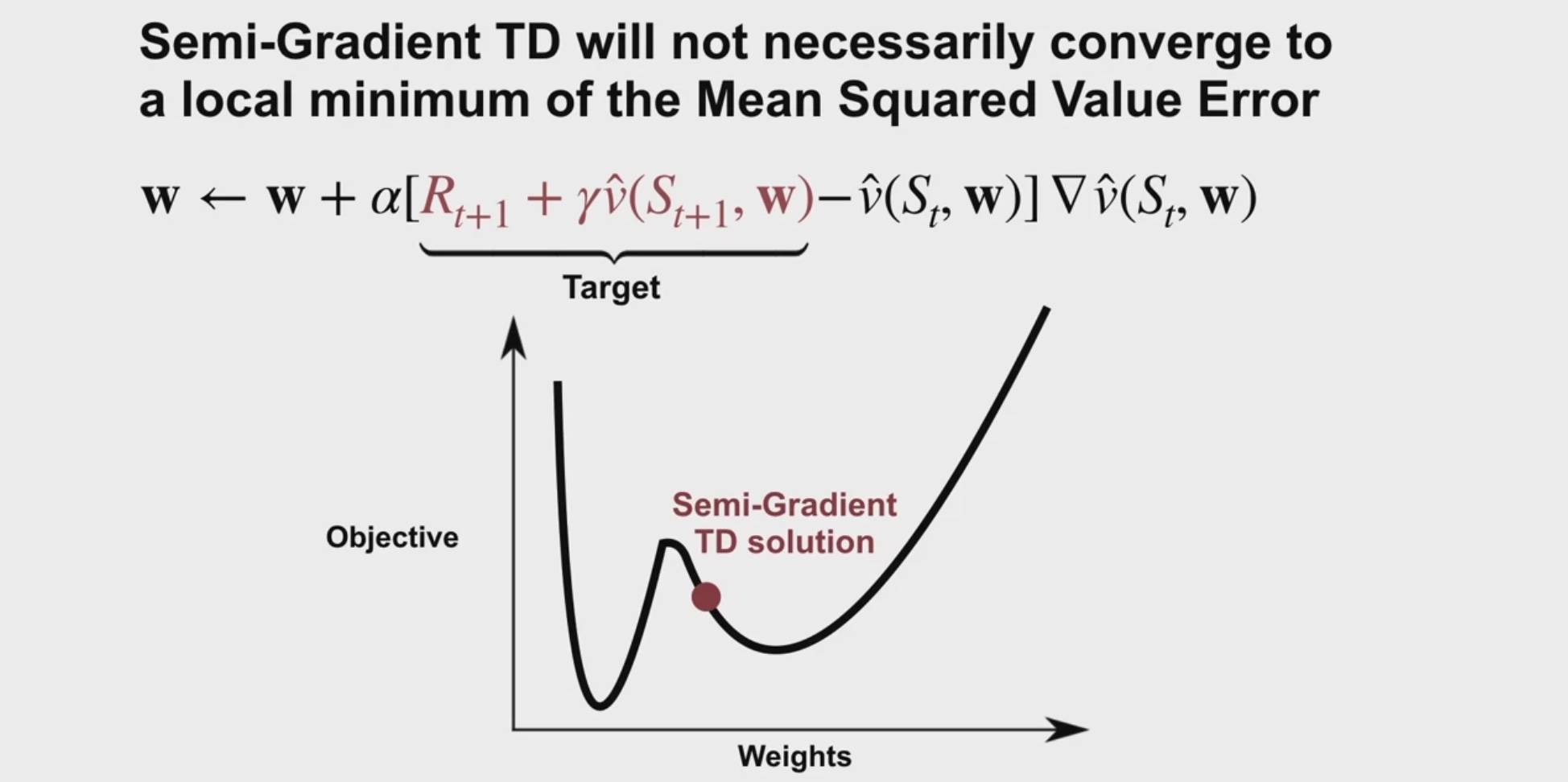
Semi-gradient TD는 local minimum로 수렴하지 않는다. (추정치를 기반으로 진행하니까)

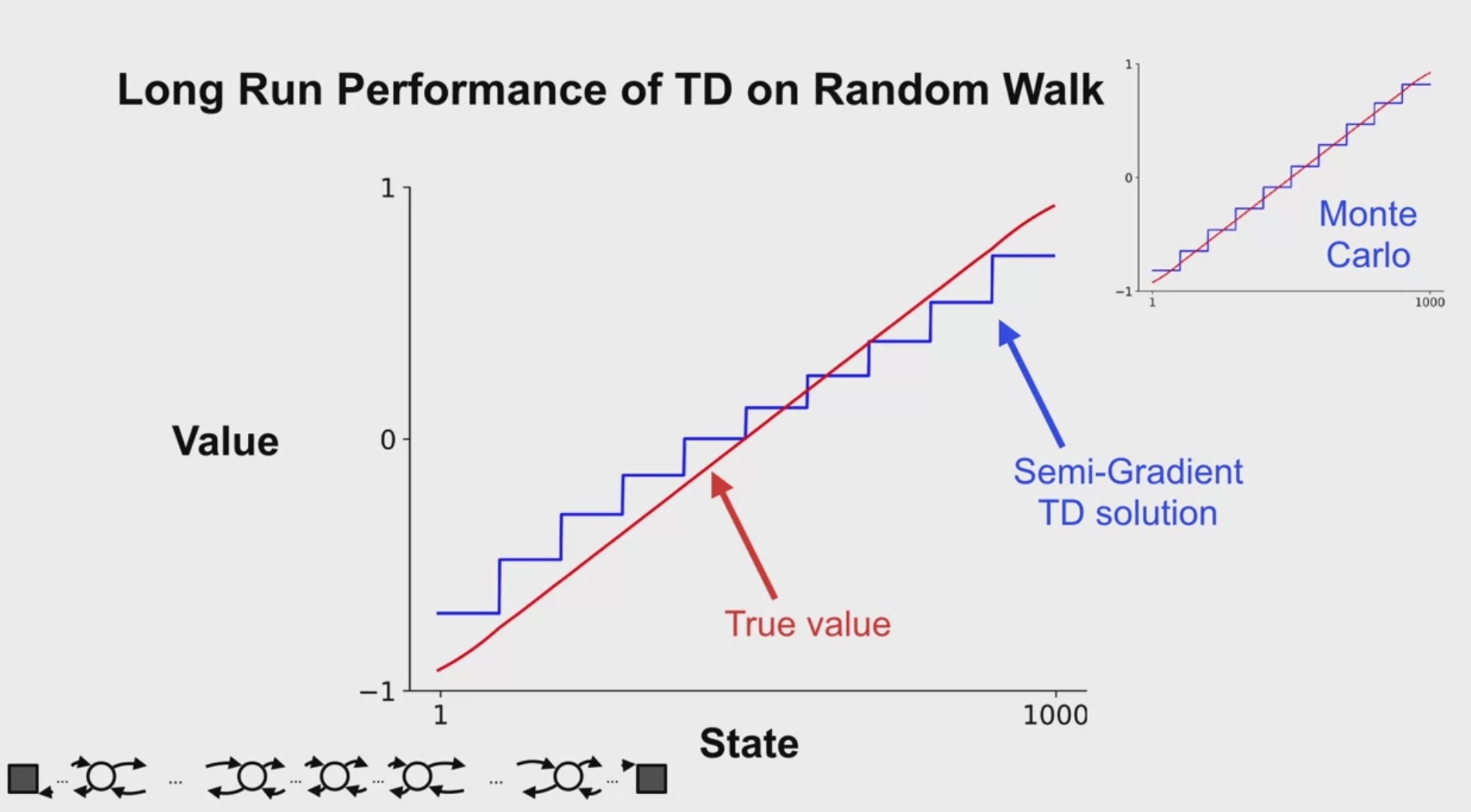
Random Walk에 적용해보면 MC보다 정확도 낮음을 볼 수 있다.

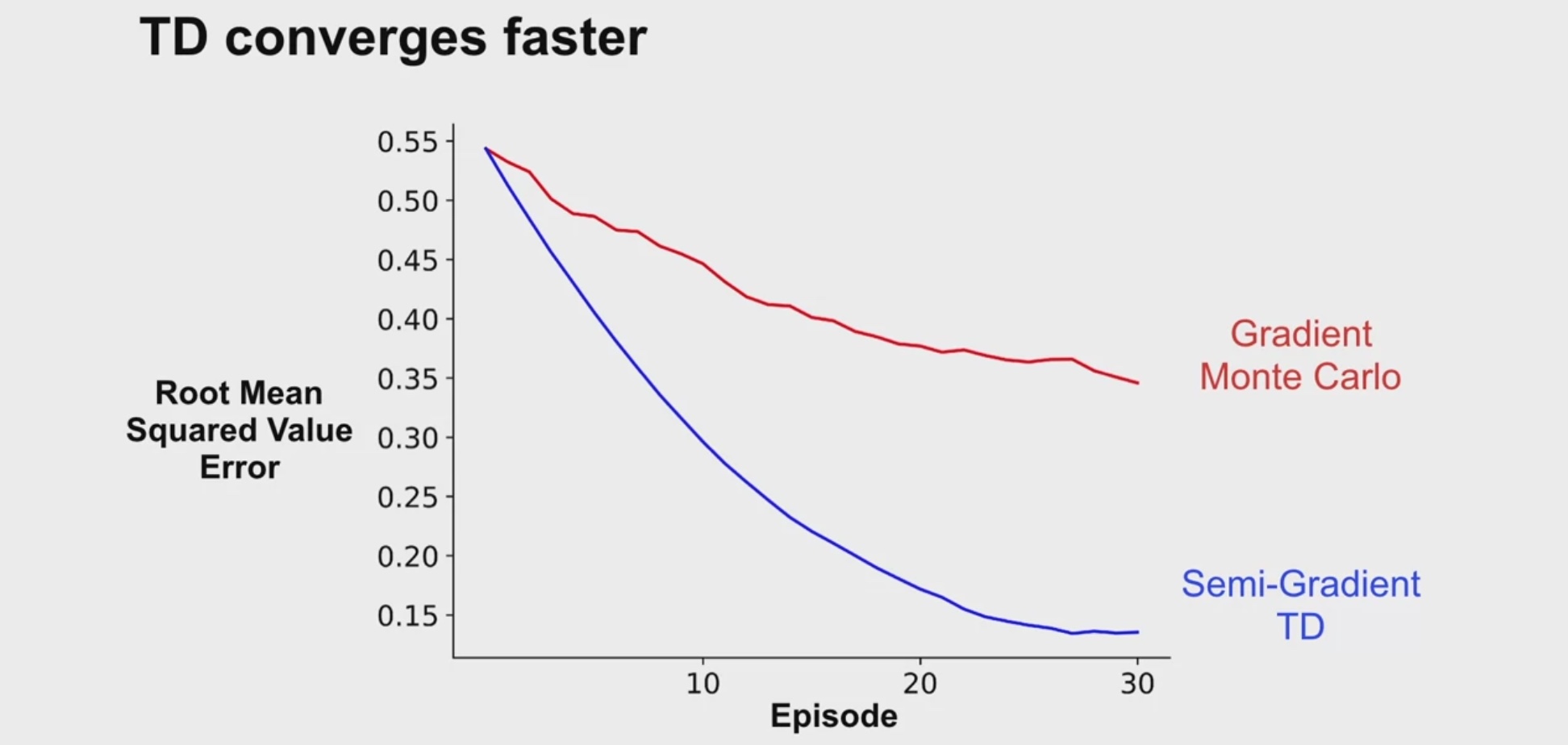
TD learns faster than Gradient MC

MC와 TD를 같은 횟수의 episode로 진행해봤을 때
최선의 step_size $\alpha$가 각각 0.01, 0.22로
TD가 더 빠르다는 것을 알 수 있다.

The Linear TD Update

TD update with linear function approximation

linear case에서 state에 대한 feature vector는
그 state의 gradient of the approximate value다.

feature가 클수록 weight는 예측에 더 크게 작용하고,
feature가 0일 경우, weight는 예측에 영향을 주지 않으며 gradient도 0이 된다.

Tabular TD(0): special case of linear semi-gradient TD(0)

Linear TD는 tabular TD와 State Aggregtation TD의 strict generalization임을 보이려 한다.

Tabular TD를 떠올려보면, feature는 하나의 state에서만 1이고 나머지는 다 0인 one-hot vector다.
Semi-gradient TD에서 feature vector X는 현재 상태에 대한 하나의 weights를 선택한다. 이 weight는 그 상태의 value estimate다.
그러므로 이 갱신은 저번 시간에 보았던 tabular TD 갱신과 일치한다.