그래프
그래프(Graph)는 데이터 구조 중 하나로, 객체 간의 관계를 나타내는 데 사용된다. 그래프는 정점(Vertex)과 간선(Edge)으로 구성되며 정점은 객체를 나타내고, 간선은 그 객체들 간의 관계를 나타낸다.
🔍 그래프의 기본 속성
정점 (Vertex)
그래프의 기본 단위로, 데이터 또는 객체를 나타낸다.
정점들은 보통 V로 표기하며, 개수는 |V|로 나타낸다.
간선 (Edge)
정점 간의 관계를 나타내는 연결선입니다.
간선들은 보통 E로 표기하며, 개수는 |E|로 나타냅니다.
📕 그래프의 종류
1. 무방향 그래프 (Undirected Graph)
간선의 방향이 없는 그래프. 즉, 두 정점 간의 연결이 양방향이다.
예: 친구 관계 (A와 B가 친구라면 B와 A도 친구)
2. 유방향 그래프 (Directed Graph)
간선에 방향이 있는 그래프. 즉, 두 정점 간의 연결이 단방향이다.
예: 트위터 팔로우 관계 (A가 B를 팔로우한다고 해서 B가 A를 팔로우하는 것은 아님)
3. 가중치 그래프 (Weighted Graph)
간선에 가중치(비용, 거리 등)가 있는 그래프.
예: 도로 네트워크 (각 도로의 길이 또는 통행 요금이 가중치로 사용됨)
4. 비가중치 그래프 (Unweighted Graph)
간선에 가중치가 없는 그래프.
5. 사이클 그래프 (Cyclic Graph)
하나 이상의 사이클(루프)을 포함하는 그래프.
예: A -> B -> C -> A
6. 비사이클 그래프 (Acyclic Graph)
사이클을 포함하지 않는 그래프.
예: 트리 (Tree)
📗 그래프의 표현 방법
1. 에지 리스트(Edge List) ⭐
간선(Edge)을 목록 형태로 나열하여 그래프를 표현한다. 에지 리스트는 간선 중심으로 그래프를 나타내기 때문에, 각 간선이 어떤 정점들 사이를 연결하고 있는지를 쉽게 확인할 수 있다.
각 간선을 정점의 쌍으로 나타내며, 이 쌍들을 리스트나 배열 등의 자료구조로 나열한다.
예 : 무방향, 유방향, 가중치
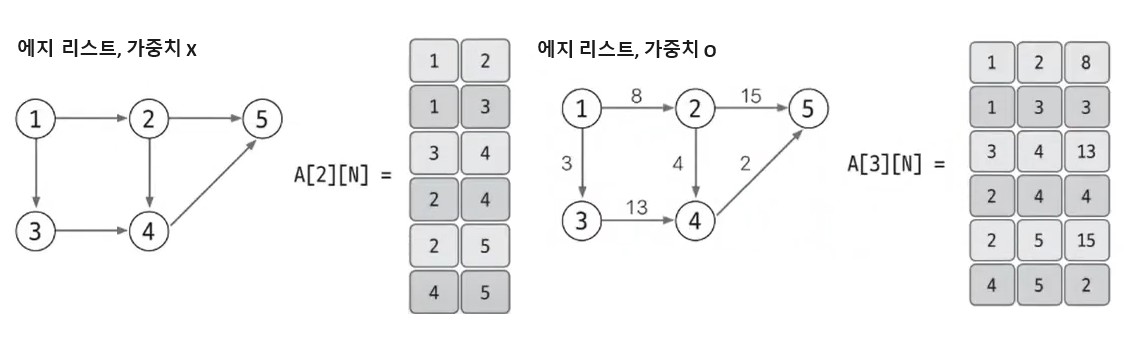
1-1. 가중치가 없을 때
가중치가 없는 간단한 무방향 그래프의 예시이다. 이 그래프는 4개의 정점과 4개의 간선으로 이루어져있다.
정점: A, B, C, D
간선: (A-B), (A-C), (B-C), (C-D)이 때 에지 리스트는 다음과 같다.
edges_unweighted = [
('A', 'B'),
('A', 'C'),
('B', 'C'),
('C', 'D')
]1-2. 가중치가 있을 때
가중치가 있는 간단한 무방향 그래프의 예시이다. 이 그래프는 4개의 정점과 4개의 간선, 가중치로 이루어져있다.
정점: A, B, C, D
간선: (A-B, 5), (A-C, 3), (B-C, 1), (C-D, 7)이 때 에지 리스트는 다음과 같다.
edges_weighted = [
('A', 'B', 5),
('A', 'C', 3),
('B', 'C', 1),
('C', 'D', 7)
]🙆♀️ 장점
매우 간단하고 간결하여, 그래프의 기본 구조를 쉽게 이해할 수 있다. 희소 그래프(sparse graph)의 경우, 에지 리스트는 인접 행렬(adjacent matrix)보다 저장 공간을 절약할 수 있다. 간선을 추가하거나 제거하는 작업이 상대적으로 간단하다.
🙅♀️ 단점특정 두 정점이 연결되어 있는지 확인하거나, 특정 정점에 연결된 모든 간선을 찾는 작업이 인접 리스트나 인접 행렬보다 느릴 수 있다. 간선의 가중치를 변경하는 작업이 상대적으로 비효율적일 수 있다.
2. 인접 행렬 (Adjacency Matrix) ⭐
2차원 배열을 사용하여 그래프를 표현한다.
정점의 개수가 n일 때, n x n 크기의 행렬로 표현된다.
행렬의 (i, j) 위치가 1이면 정점 i와 j가 연결되어 있음을 나타낸다.
1-1. 가중치가 없을 때
가중치가 없는 간단한 무방향 그래프의 예시이다. 이 그래프는 4개의 정점과 4개의 간선으로 이루어져있다.
정점: A, B, C, D
간선: (A-B), (A-C), (B-C), (C-D)이 때 인접 행렬은 다음과 같다.
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 1 | 0 |
| B | 1 | 0 | 1 | 0 |
| C | 1 | 1 | 0 | 1 |
| D | 0 | 0 | 1 | 0 |
adj_matrix_unweighted = [
[0, 1, 1, 0],
[1, 0, 1, 0],
[1, 1, 0, 1],
[0, 0, 1, 0]
]1-2. 가중치가 있을 때
가중치가 있는 간단한 무방향 그래프의 예시이다. 이 그래프는 4개의 정점과 4개의 간선, 가중치로 이루어져있다.
정점: A, B, C, D
간선: (A-B, 5), (A-C, 3), (B-C, 1), (C-D, 7)이 때 인접 행렬은 다음과 같다.
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 5 | 3 | 0 |
| B | 5 | 0 | 1 | 0 |
| C | 3 | 1 | 0 | 7 |
| D | 0 | 0 | 7 | 0 |
adj_matrix_weighted = [
[0, 5, 3, 0],
[5, 0, 1, 0],
[3, 1, 0, 7],
[0, 0, 7, 0]
]🙆♀️ 장점
두 정점 사이에 간선이 존재하는지 여부를 O(1) 시간에 확인할 수 있다. 그래프 이론과 행렬 연산을 결합하여 다양한 알고리즘을 효율적으로 구현할 수 있다. 정점의 수가 고정된 경우, 데이터 구조가 간단하고 관리하기 쉽다.
🙅♀️ 단점희소 그래프(sparse graph)의 경우, 대부분의 요소가 0이어서 많은 공간을 낭비하게 된다. 정점을 추가하거나 삭제하는 작업이 인접 리스트에 비해 더 복잡하고 비효율적이. 연결된 모든 간선을 찾는 데 시간이 더 오래 걸릴 수 있다.
3. 인접 리스트 (Adjacency List) ⭐
각 정점에 대한 리스트를 사용하여 그래프를 표현한다.
정점 i에 연결된 모든 정점의 리스트로 표현된다.
공간 효율성이 높아 일반적으로 많이 사용된다.
1-1. 가중치가 없을 때
가중치가 없는 간단한 무방향 그래프의 예시이다. 이 그래프는 4개의 정점과 4개의 간선으로 이루어져있다.
정점: A, B, C, D
간선: (A-B), (A-C), (B-C), (C-D)이 때 인접 리스트는 다음과 같다.
adj_list_unweighted = {
'A': ['B', 'C'],
'B': ['A', 'C'],
'C': ['A', 'B', 'D'],
'D': ['C']
}1-2. 가중치가 있을 때
가중치가 있는 간단한 무방향 그래프의 예시이다. 이 그래프는 4개의 정점과 4개의 간선, 가중치로 이루어져있다.
정점: A, B, C, D
간선: (A-B, 5), (A-C, 3), (B-C, 1), (C-D, 7)이 때 인접 리스트는 다음과 같다.
adj_list_weighted = {
'A': [('B', 5), ('C', 3)],
'B': [('A', 5), ('C', 1)],
'C': [('A', 3), ('B', 1), ('D', 7)],
'D': [('C', 7)]
}🙆♀️ 장점
희소 그래프의 경우 인접 리스트는 인접 행렬보다 훨씬 적은 공간을 사용한다. 특정 정점에 인접한 모든 정점을 순회하는 작업이 빠르다. 간선의 추가 및 삭제가 상대적으로 간단하고 빠르다.
🙅♀️ 단점두 정점 사이에 간선이 존재하는지 확인하는 작업이 인접 행렬보다 느리다. 최악의 경우 O(n) 시간이 걸릴 수 있다. 특정 정점에 인접한 정점들을 찾는 데 추가적인 리스트 순회가 필요할 수 있다.
📘 그래프 탐색 알고리즘
깊이 우선 탐색 (Depth-First Search, DFS) ⭐
스택 또는 재귀를 사용하여 그래프를 탐색한다.
한 정점에서 출발하여 갈 수 있는 한 끝까지 탐색하고, 더 이상 갈 곳이 없으면 이전 정점으로 돌아와 다시 탐색한다.
너비 우선 탐색 (Breadth-First Search, BFS) ⭐
큐를 사용하여 그래프를 탐색한다.
한 정점에서 출발하여 인접한 모든 정점을 탐색하고, 그 다음 정점으로 이동하여 다시 인접한 모든 정점을 탐색한다.
💻 빈출 예제
1. 네트워크 연결 문제
인터넷 라우터 간의 데이터 전송 경로를 찾는 문제
최단 경로 알고리즘 (다익스트라 알고리즘 등) 활용
2. 소셜 네트워크 분석
사용자 간의 관계를 그래프로 모델링하여 분석
연결 요소, 중심성, 커뮤니티 탐지 등
3. 지도 및 경로 찾기
도시 간의 도로 네트워크를 그래프로 표현
최단 경로, 최단 거리 등 경로 찾기 문제
4. 프로젝트 관리
작업 간의 선후 관계를 그래프로 표현
작업 스케줄링, 임계 경로 분석 등

