0. 그래프의 표현

그래프를 구현하는 3가지 방법이 있습니다.

오늘 그 세가지가 뭔지 알아봅시다.

'Do it! 알고리즘 코딩테스트 with Python(김종관 저)'을 공부하고 정리한 내용입니다.

1. 에지 리스트

• 에지를 중심으로 그래프를 표현
• 배열에 출발 노드, 도착 노드를 저장하여 에지를 표현 또는 출발 노드, 도착 노드, 가중치를 저장하여 가중치가 있는 에지를 표현

1-1. 에지 리스트로 가중치 없는 그래프 표현하기

• 가중치가 없는 그래프는 출발 노드와 도착 노드만 표현합니다. -> 배열의 열 2개 충분
• 노드는 여러 자료형 사용 가능
• 방향이 있는 그래프 예시
• 
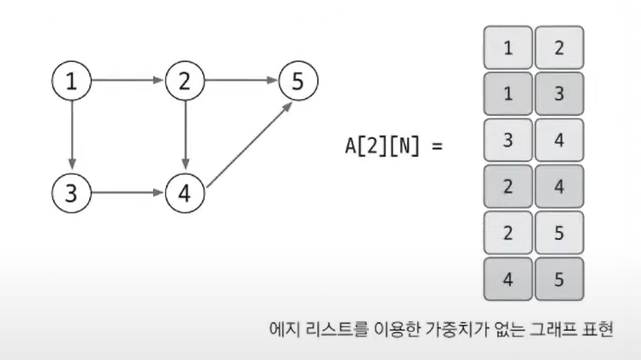
• 방향이 없는 그래프라면, [1,2]와 [2,1]은 같은 표현일 것입니다.

1-2. 에지 리스트로 가중치 있는 그래프 표현하기

• 가중치가 있는 그래프는 행을 3개로 늘려 3번째 행에 가중치를 저장합니다.
• ex) 1에서 2로 향하는 가중치가 8인 에지는 [1,2,8]로 표현

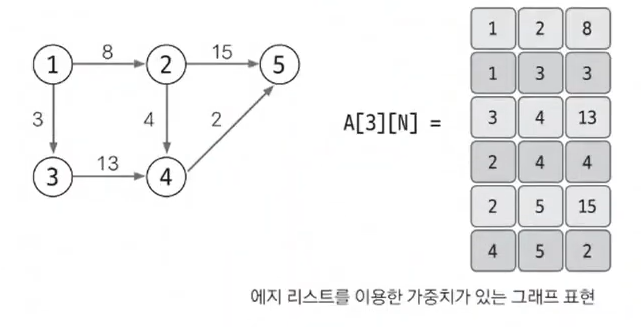
[특징]

• 구현하기 쉽다.
• 특정 노드와 관련되어 있는 에지를 탐색하기는 쉽지않다.
• 벨만 포드나 크루스칼(MST)알고리즘에 사용, 노드 중심 알고리즘에는 잘 사용하지 않는다.

2. 인접 행렬

인접행렬은 2차원 배열을 자료구조로 이용하여 그래프를 표현합니다. 인접 행렬은 에지 리스트와 다르게 노드 중심으로 그래프를 표현합니다.
그림으로 자세히 이해해봅시다.

2-1. 인접 행렬로 가중치 없는 그래프 표현하기

• 1에서 2로 향하는 에지를 1행 2열에 1을 저장하는 방식으로 표현
• 1을 저장하는 이유는 가중치가 없기 때문

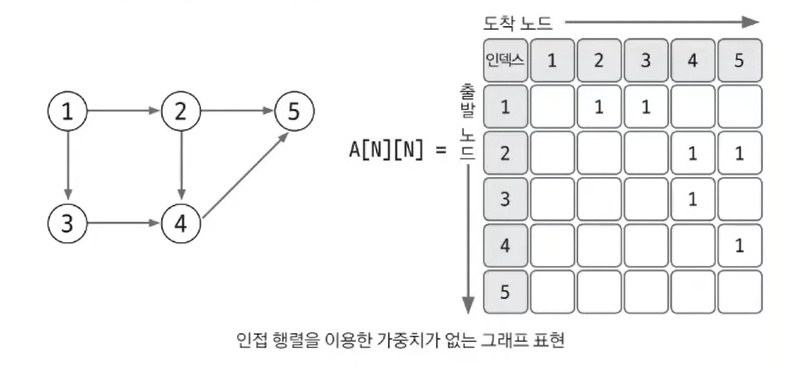
2-2. 인접 행렬로 가중치 있는 그래프 표현하기

• 2에서 5로 향하는 에지를 2행 5열에 15를 저장하는 방식으로 표현

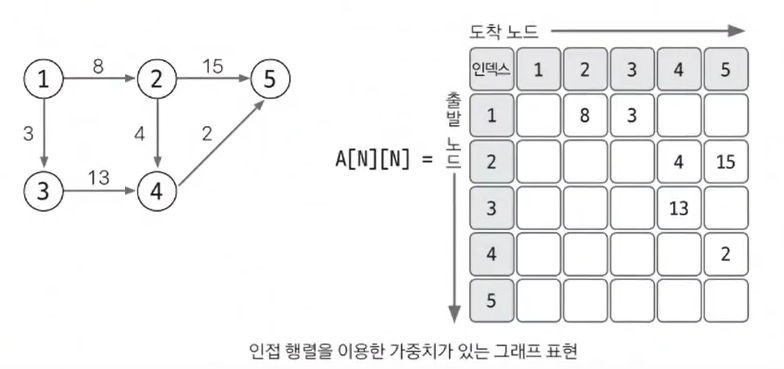
[특징]

• 구현하기 쉬움
• 두 노드를 연결하는 에지의 여부와 가중치값을 배열에 직접 접근하면 바로 확인할 수 있음
• 노드와 관련되어있는 에지를 탐색하려면 N번 접근해야하므로 노드 개수에 비해 에지가 적을 때는 공간 효율이 떨어짐
• 노드 개수가 많은 경우 아예 2차원 배열 선언 자체를 할 수 없는 결함도 있다.
  -> 인접 행렬은 노드 개수에 따라 사용 여부를 적절히 판단해야한다.
  -> 예 ) 노드가 3만개 넘으면 자바 힙 스페이스 에러가 발생!

3. 인접 리스트

인접 리스트는 ArrayList로 그래프를 표현합니다.
노드 개수 만큼 ArrayList를 선언합니다.
자료형은 경우에 맞게 사용합니다.

3-1. 인접 리스트로 가중치 없는 그래프 표현하기

N번 노드와 연결되어 있는 노드를 배열의 위치 N에 연결된 노드 개수만큼 배열을 연결하는 방식으로 표현

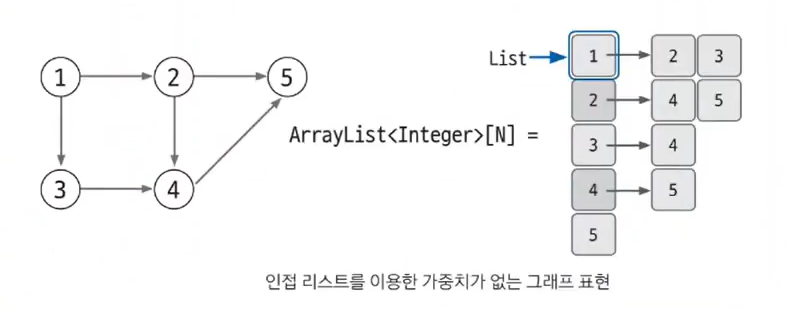
노드1과 연결된 노드 2,3은 ArrayList[1]에 [2,3]을 연결한다.

3-2. 인접 리스트로 가중치 있는 그래프 표현하기

가중치가 있는 경우 자료형을 클래스로 사용합니다.
다음은(도착 노드, 가중치)를 갖는 Node클래스를 선언하여 ArrayList에 사용한 것입니다.

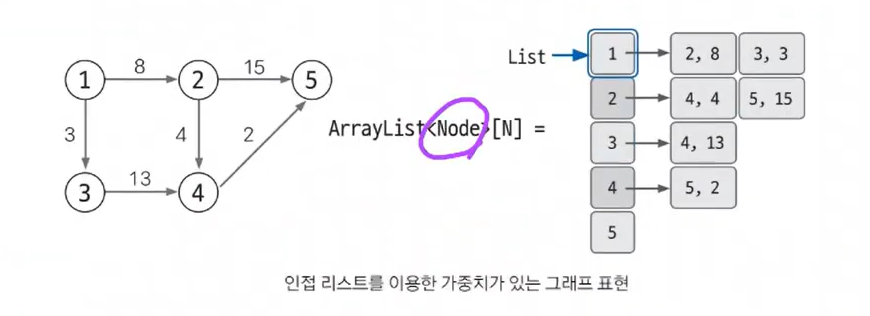
그림을 보면, ArrayList[1]에 [(2,8),(3,3)]이 연결되어있다.
-> 노드1과 2가 가중치 8 에지로, 노드 1과 3이 가중치 3 에지로 연결되어있다는 뜻

[특징]

• 다른 방법에 비해 구현이 복잡한 편
• 노드과 연결되어 있는 에지를 탐색하는 시간은 매우 뛰어나다.
• 노드 개수가 커도 공간 효율이 좋아 메모리 초과 에러도 발생하지 않는다.
• 여러 장점으로 실제 코딩테스트에서는 인접 리스트를 이용한 그래프 구현을 선호한다!